修復狀態不確定的巡回修理任務多目標動態調度
劉 彥, 陳春良, 陳偉龍, 范江波
(1. 陸軍裝甲兵學院裝備保障與再制造系, 北京100072; 2. 中國衛星海上測控部, 江蘇 江陰 214431, 3. 66058部隊, 天津 301700)
現代戰爭作戰節奏越來越快,作戰進程不斷縮短,作戰空間逐漸變廣,使得戰損裝備多、戰時裝備保障時間縮短,維修任務繁重,對戰時裝備維修的時效性提出了更高的要求。巡回修理作為戰時裝備維修的主要修理方式之一,通過派遣多個巡回修理組對分布在戰場的眾多待修裝備實施搶救修理,實現作戰部隊戰斗力的保持與恢復。
面對眾多隨機出現的不同損傷程度的待修裝備,如何在有限的修理時間內,綜合權衡待修裝備位置、修理工作量、重要度、各巡回修理組的修理能力及其變化等復雜因素,合理安排巡回修理任務,解決“先修誰”“由誰修”“何時修”“怎么修”的戰時裝備維修任務調度問題,從而實現維修效益全局最優化,是具有重大意義且亟待解決的軍事難題。
由于戰場態勢復雜、約束條件多、研究難度大,眾多學者對裝備維修任務調度進行了深入探索,取得了一定成果,具有一定的指導意義。如:張立民等[1]分析了戰時裝備維修任務調度的特點,建立了基于最大保障時間的維修任務靜態調度模型;王正元等[2]以盡快恢復裝備戰斗力為目標,探究了動態維修任務調度的優化方法;陳春良等[3]考慮時間約束及負載能力約束的影響,將裝備維修任務調度問題轉化為車輛路徑問題,并設計了基于改進最大最小螞蟻算法(Max-Min Ant System,MMAS)的維修任務規劃方法,實現了單修理組的維修任務調度;陳偉龍等[4]提出了進攻作戰搶修任務動態調度問題,將其抽象為動態車輛路徑問題,以獲得的二次作戰時間最大為調度目標構造了調度模型,并設計了變體遺傳算法(Genetic Algorithm,GA)進行模型求解。
從模型抽象的角度來看,裝備維修任務調度問題主要可抽象為車間作業調度問題[1]、資源約束項目調度問題[5]以及車輛路徑問題[4,6],其中前二者適用于基地級修理及定點修理,后者更適用于伴隨修理及巡回修理。隨著裝備維修任務調度研究的不斷深入,調度目標根據任務需求(如維修效益[7]、裝備重要度[8]、二次作戰時間[9]等)不斷豐富,但大多數研究僅限于單目標調度;另一方面,約束條件根據戰場情況不斷細化,但主要聚焦在傳統約束,如考慮裝備維修流程[10]、維修專業[11]、維修力量休息[5]、不確定性[12-13]等。陳春良等[9]考慮戰場搶修時修理能力的限制,提出了非遍歷型調度,符合戰時修理實際,具有一定指導意義;陳偉龍等[12]雖然考慮了待修裝備修復狀態,但僅僅停留在對完成任務數的影響,并未考慮修復狀態對維修時間及裝備重要度的影響。
總體來看,現階段裝備維修任務調度研究尚未針對修理方式的差異進行研究,也未對巡回修理中如何合理規劃諸多實際約束下維修任務以及動態處理不確定性信息問題進行深入研究。現有研究大多數是以最大保障時間、最長二次作戰時間等作為單一調度目標進行任務調度,難以全面考慮維修任務需求,且約束條件相對較為理想化,忽略了修復狀態的不確定性及其對維修時間和裝備重要度的影響,也未考慮時間窗約束對維修任務調度的影響。
針對以上問題,筆者以戰時裝備巡回修理任務調度問題為研究對象,考慮待修裝備修復狀態的不確定性及其對維修時間和裝備重要度的影響,引入待修裝備修理時間窗約束及非遍歷約束,考慮待修裝備的不確定性,構建了多個裝備巡回修理組任務動態調度模型,設計了改進的NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm Ⅱ)算法對模型進行求解,并通過示例驗證了模型及算法的有效性及合理性。
1 基本描述
1.1 問題描述
隨著作戰進程的推進及作戰任務的遂行,受敵方火力打擊的影響,我方作戰裝備不可避免地會在不同時間、不同地點出現不同程度的損傷。巡回修理力量編成多個巡回修理組,根據待修裝備損傷及分布情況,有計劃地對分布在戰場各地域的待修裝備進行巡回修理,既可相對有規律地遂行保障,又可對突然出現的待修裝備做出快速反應。在一體化指揮信息平臺的支撐下,各待修裝備的位置、預計修理時間以及裝備重要度等信息可通過相應手段獲知。各巡回修理組從初始地域出發,前往各待修裝備所在地域實施巡回修理,完成各自修理任務后不返回初始地域,而是根據保障指揮員的安排執行后續任務。在實施修理任務的過程中,保障指揮員會根據不斷更新的待修裝備及各巡回修理組信息,對各巡回修理組的修理計劃進行動態調度。
在待修裝備不斷出現,而修理時間及修理能力有限的前提下,需考慮待修裝備修理時間、重要度、修復狀態的不確定性、巡回修理組修理能力的變化等因素的影響,從而為各巡回修理組合理分配維修任務,確定各巡回修理組的各待修裝備的修理順序和修復狀態,并根據不斷出現的待修裝備及諸多不確定因素對維修任務進行動態調整,使整體的巡回修理效果達到最優化,最有利于戰斗力的快速恢復及作戰任務的完成。
1.2 假設描述
為了簡化問題,進行如下假設:
1) 參與裝備巡回修理任務調度的各待修裝備均在巡回修理組的修理能力范圍內,不考慮備品備件短缺情況;
2) 研究對象為合成旅巡回修理力量,編成多個巡回修理組對所屬部隊實施全域巡回修理;
3) 在修理任務實施過程中,各巡回修理組獨立完成各自修理任務,相互獨立,不存在相互支援;
4) 各待修裝備的位置、預計修理時間、修理時間窗、裝備重要度等相關信息已通過技術偵察獲知;
5) 各修理組修理過程中不會由于任務調整而中止當前正在執行的任務;
6) 各巡回修理組完成修理任務后不返回初始地域,而是等待保障指揮員的后續指揮調度;
7) 待修裝備修復后直接歸建作戰部隊并參與作戰,忽略歸建時間;
8) 不考慮敵方火力打擊對待修裝備造成的二次傷害。
2 模型構建
2.1 參數定義
為方便研究,對相關參數定義如下:
1)Tsta為戰斗開始時刻,Tbeg為巡回修理開始時刻,Tend為戰斗結束時刻。
2)E為待修裝備集合,且|E|=n,n為待修裝備數量,H為始發點集合。

4)ti為待修裝備i出現的時刻,(xi,yi)為待修裝備i的位置坐標,其修理時間窗為[ti,Tiup],其中Tiup為修理窗時間上限。

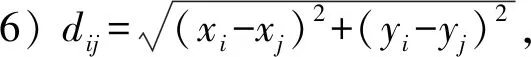

8)pk為第k個巡回修理組的修理能力,即每小時能提供的人時。

10)α為懲罰系數,用以表征時間窗對裝備重要度的影響。
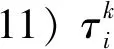
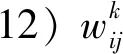

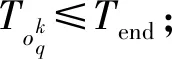
14)qk為第k個巡回修理組修理路徑中的截點,表示該組最終實際修理的最后一臺裝備,且有
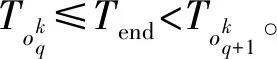
2.2 多目標參數確定
實施戰時裝備巡回修理旨在最大可能地修復待修裝備,使其能盡快返回戰場繼續參與戰斗,以發揮修竣裝備對裝備體系的貢獻,使作戰部隊的戰斗力能得到最大程度的恢復。因此,可從以下3個方面來綜合衡量裝備巡回修理任務調度的優劣。
1) 修竣裝備總數。修竣裝備總數是整個戰斗過程中各巡回修理組修復的待修裝備數量總和,它反映了巡回修理的快慢程度,直接影響裝備的參戰率,其表達式為
(1)
2) 修竣裝備總重要度。修竣裝備總重要度是修竣裝備重要度的總和,反映了所修竣裝備對整個裝備體系的貢獻度,是巡回修理重要性的反映,其表達式為
(2)
3) 二次作戰總時間。二次作戰總時間是指各修竣裝備從修竣時刻至戰斗結束時刻的時間長度的總和,反映了裝備修竣后返回戰場參戰的有效時長,是修理及時程度的體現,其表達式為
(3)
以上3個參數從不同側面反映巡回修理效果,且相互影響、相互制約,需要構建多目標優化模型來實現全局的綜合權衡。
2.3 調度模型建立
結合巡回修理特點,考慮各巡回修理組修復各待修裝備的修理時間關系、遍歷與非遍歷特點、待修裝備修竣與否,確定相關約束條件,構建裝備巡回修理任務調度模型如下:
(4)
(5)
(6)
其中,式(4)-(6)表示面向裝備巡回修理的任務調度目標分別為修竣裝備總數最大、修竣裝備總重要度最大、獲得的二次作戰總時間最長;式(7)表示巡回修理組從初始位置前往并修竣該組計劃內第一臺待修裝備的時間關系;式(8)表示巡回修理組修理計劃內相鄰2臺待修裝備的修竣時刻的約束關系;式(9)表示修理時間以及修理能力的約束關系;式(10)表示巡回修理組的遍歷與非遍歷約束;式(11)表示每個待修裝備至多僅由一個巡回修理組修理一次;式(12)、(13)表示任意一條弧線的終點(起點)待修裝備有且僅有一個起點(終點)待修裝備與之相連。
2.4 調度模型分析
2.4.1 多目標分析
裝備巡回修理任務調度模型從修理數量、修理對象重要程度以及修理及時性3個方面權衡維修任務調度方案的優劣,能夠克服傳統維修任務調度單純追求某一目標而導致調度方案在其他需求方面存在較大偏差的問題,從而能夠更加全面地權衡維修任務調度方案的優劣。
Pareto解集[14]通過支配關系判斷調度方案的優劣,能夠實現各調度目標間的均衡,是處理多目標調度問題的較好思路。通過在多個目標中協調平衡,可獲得一組可接受解(即Pareto最優解集),從而增加了保障指揮員的決策余地。保障指揮員可根據戰場實際需求及決策偏好從Pareto最優解集中選擇滿意的調度方案。
設定滿意方案的決策策略為通過對Pareto最優解集中的解進行規范化處理,采用加權法進行排序優選,從而選擇滿意解,即
(14)
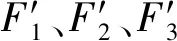
2.4.2 修復狀態的不確定性
巡回修理相對于伴隨修理而言,修理開始的時間相對滯后、待修裝備相對較多且損傷程度更嚴重。由于修理時間的限制,為了使待修裝備盡快得到修復并返回戰場參戰,待修裝備的修復狀態并不全是完全修復,而有可能是僅恢復了部分功能,即待修裝備的修復狀態分為“能正常作戰”S1和“能應急作戰”S2。
待修裝備修復至不同狀態對維修任務調度均產生較大影響,主要是所需的修理工時和修復后獲得的裝備重要度不同。因此,在制定調度方案時,不但要確定各待修裝備的修理順序,還需確定各待修裝備的修復狀態,這使得維修任務調度問題更為復雜,求解難度更大,但同時也更貼近實際,具有更強的實用性。
2.4.3 修理時間窗
由于修理能力的限制,難以實現所有待修裝備在第一時間均得到修復。隨著作戰階段、作戰任務的變化,當超過某一時刻待修裝備仍未得到修復,該待修裝備的重要度將會受到影響。因此借鑒車輛路徑問題中的時間窗[15]概念,引入待修裝備修理時間窗,對超出修理時間窗而未得到修復的待修裝備重要度進行懲罰,其懲罰公式如下:
(15)

2.4.4 非遍歷性
巡回修理組負責全域的巡回修理,待修裝備多、修理難度大,而受修理時間及修理能力的限制,難以對散布在戰場的各待修裝備實現全部修復。在調度初期,參與調度的待修裝備較少,在任務規劃時一般可實現遍歷修理(即對全部待修裝備進行修理),但隨著作戰進程的推進,待修裝備不斷增多,無法對參與調度的眾多待修裝備實現全部修復,需采用非遍歷型調度。
2.4.5 修理能力變化
戰時各巡回修理組的修理能力存在差異,且受戰場環境等諸多因素影響,各巡回修理組的修理能力會隨著修理任務的遂行而逐漸發生變化。主要體現在隨著修理任務的實施,修理人員會產生疲勞,從而影響修理效率,使巡回修理組的修理能力發生變化。
修理人員疲勞所導致的修理能力變化可通過修理效率來度量,其計算公式為
(16)
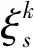
待修裝備的修理時間不但與所承擔修理的巡回修理組有關,還受其修理順序的影響,導致裝備維修任務調度更加復雜。
2.4.6 動態驅動策略分析
在處理裝備維修任務動態調度問題時,引入滾動時域思想[11],根據調度需求將整個任務剖面轉換為一系列離散時間點的靜態調度問題,通過多次維修任務調度,實現動態問題靜態處理。而動態驅動策略就是設定某一驅動條件用以判斷該時刻是否需要對維修任務進行再次調度,是動態調度的基礎。

該動態調度策略在每次重調度時,更新巡回修理組及參與調度的待修裝備信息,消除待修裝備的實際修理時間與計劃修理時間差所產生的調度誤差,在實現維修任務動態調度的同時也提升了動態調度的可靠性。
3 模型求解
裝備巡回修理任務調度模型是一個存在諸多約束的多目標調度模型,針對模型特點,筆者結合Pareto解集思想,設計了改進遺傳算法來求解裝備巡回修理任務多目標動態調度問題。
3.1 Pareto最優解集構建
傳統多目標優化方法通過線性加權或目標規劃等方法處理多目標調度問題,其本質是將多目標問題轉化為一個或一系列單目標優化問題進行求解,難以解決多個優化目標之間的沖突關系,存在依賴先驗知識、難以處理Pareto最優前端非凸等問題。NSGA-II算法作為最優秀的多目標進化算法之一,在保證種群多樣性及保護種群優良個體的同時降低了計算復雜度[16]。因此,筆者通過NSGA-II算法的精英策略,采用非支配排序方法并結合擁擠度比較算子,獲得Pareto最優解集,為保障指揮員提供決策依據。保障指揮員可根據戰場態勢及實際需求,依托決策偏好及決策策略,在Pareto最優解集中選擇最滿意解。
3.2 編碼與解碼設計
考慮裝備巡回修理任務調度具有多個巡回修理組、非遍歷性以及待修裝備修復狀態不確定性等特點,設計3段式編碼以實現相關約束:前段采用順序編碼,用于表示巡回修理組的任務分工;中段采用“1-2”整數編碼,用于表示待修裝備的修復狀態,1表示修復狀態為S1,2表示修復狀態為S2;后段采用整數編碼,表示斷點位置,用于劃分各巡回修理組。該編碼方式能實現多個巡回修理組的非遍歷約束以及待修裝備修復狀態不確定性約束,且染色體與解一一對應,避免了遺傳操作中不可行解的產生,大大提高了算法收斂速度。解碼時,選取目標函數作為適應度函數,通過相關約束,計算求得截點的信息及相應適應值,從而實現解碼。
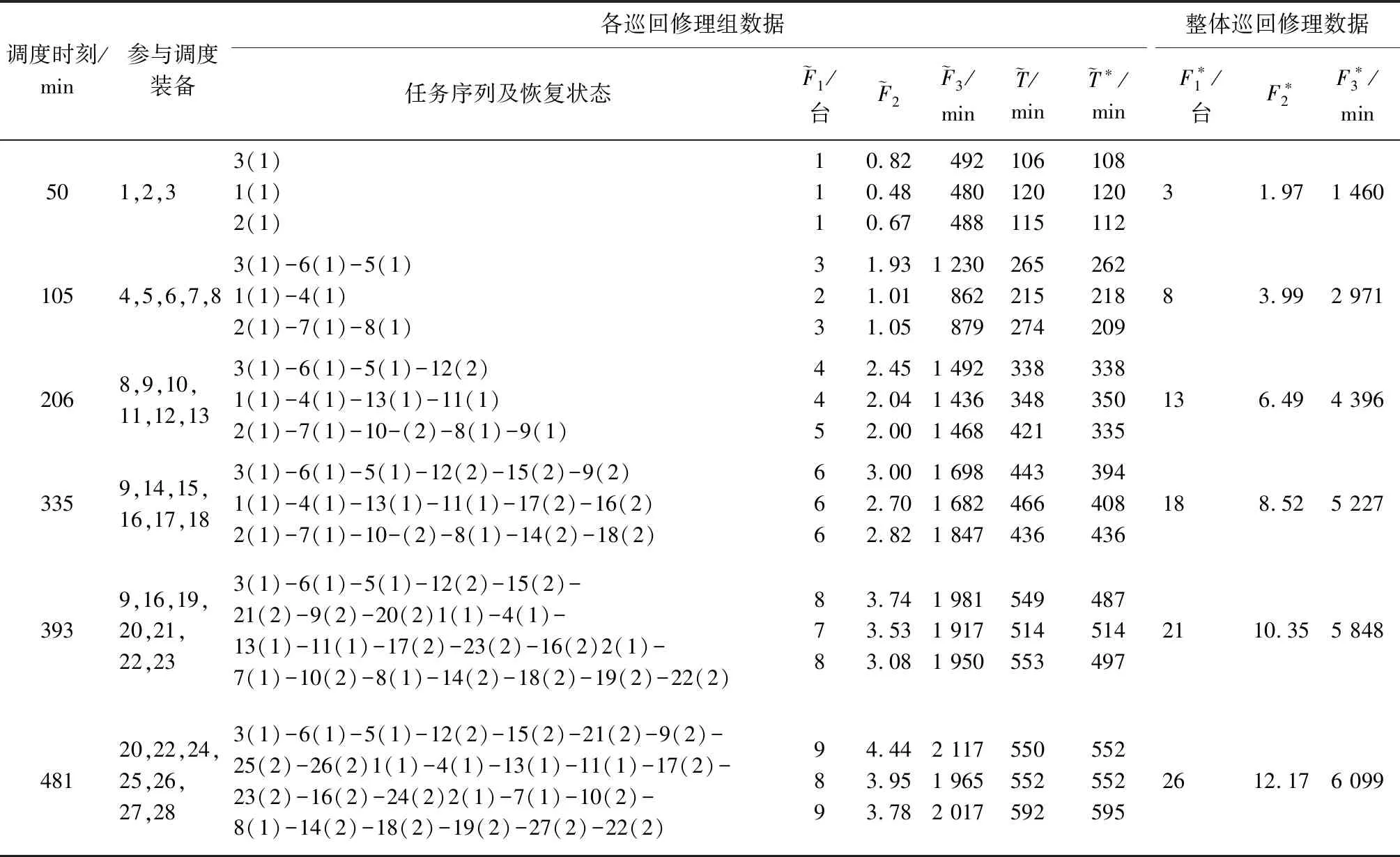
編碼及解碼示例如圖1、2所示,其中染色體X=(4,8,2,6,3,10,7,5,1,9,1,1,2,1,2,2,1,2,1,1,3,7),n=10,m=3。經解碼可知,共有3個巡回修理組負責10臺待修裝備的修理任務,任務計劃安排為:巡回修理組1的任務安排及修理順序為4-8-2,修復狀態分別為S1、S1、S2;巡回修理組2的任務安排及修理順序為6-3-10-7,修復狀態分別為S1、S2、S2、S1;巡回修理組3的任務安排及修理順序為5-1-9,修復狀態分別為S2、S1、S1。截點信息為(1,5,8),表明受諸多約束的影響,部分待修裝備并未來得及修復,最終實際修理任務完成情況為:巡回修理組1修竣待修裝備4,修復狀態為S1;巡回修理組2修竣待修裝備6-3,修復狀態為S1、S2;巡回修理組3修竣待修裝備5,修復狀態為S2。適應值分別為F1、F2、F3。

圖1 編碼示例

圖2 解碼示例
3.3 遺傳算子設計
3.3.1 父染色體選擇
根據NSGA-II算法中的非支配排序和個體間擁擠距離得到比較算子,采用BTS(Binary Tournament Selection)從上一代染色體中選取20%的個體作為父染色體進行后續交叉變異操作。
3.3.2 交叉變異
由于染色體采取3段式編碼,各段編碼的編碼方式及其實際意義不同,其交叉變異無法采用傳統方式進行。為了增大種群多樣性,提高收斂速度,針對編碼特點,確定“前段只進行變異操作,中段和后段可進行交叉及變異操作”思路,設計了相應遺傳算子,對每條父染色體進行如下遺傳操作:1)前段、后段均采用隨機更新操作;2)前段采取隨機更新,后段采取倒置操作;3)前段采用倒置操作,后段采用隨機更新操作;4)前段采用倒置操作,后段采用滑動平移操作;5)前段不采取操作,后段采用隨機更新操作。
3.4 算法流程設計
模型求解步驟如下:
1) 初始化相關參數。主要是確定種群規模pop_size、最大迭代次數num_gen等,并隨機產生初始種群P0。
2) 對種群P0中任一染色體進行解碼,計算其適應值和截點信息,得到初始化可行解種群O,并記為pop_chrom。
3) 根據NSGA-Ⅱ算法對可行解種群O進行快速非支配排序,計算非支配集個體間擁擠距離,并令gen=1。
4) 根據BTS從pop_chrom中隨機選出數量規模為pop_size的父代染色體種群parent_chrom。通過遺傳算子進行遺傳操作,產生子代染色體種群offspring_chrom,并計算offspring_chrom中任一染色體的截點信息及其適應值。
5) 采用NSGA-Ⅱ算法對pop_chrom及offspring_chrom進行快速非支配排序,計算非支配集個體間擁擠距離,根據BTS從pop_chrom及offspring_chrom中篩選出規模為pop_size的新一代染色體pop_chrom,從而實現父代優秀個體基因的精英保留。
6) 判斷是否gen 7) 判斷重調度驅動策略是否滿足。若滿足,轉入步驟1)進行重調度;否則運算終止,輸出調度結果。 某合成旅受上級指示執行機動進攻任務,受敵方火力打擊,經過一段時間后,陸續出現待修裝備,在一體化指揮信息網絡的支撐下,經技術偵察,各待修裝備相關信息均已獲知,保障指揮員根據已知信息,派遣3個巡回修理組對全旅實施全域保障,各巡回修理組遂行巡回修理任務,負責修理120 min內能完成的待修裝備。 戰斗初期(t≤300 min),需要更多、更重要的裝備及時參戰,取μ1=0.2,μ2=0.6,μ3=0.2,戰斗后期(t>300 min),需要提供更多的作戰時間,取μ1=0.3,μ2=0.2,μ3=0.5。 根據巡回修理組的實際機動時間、修理時間以及調度策略對裝備維修任務進行動態調度,得到調度規劃結果如表2所示。 表1 待修裝備信息 表2 調度規劃結果 此次裝備巡回修理任務調度共經歷了6次調度過程,在MATLAB軟件平臺用時分別為11.45、10.87、9.68、9.75、8.32、9.06 s。最終裝備巡回修理路徑規劃如圖3所示。 圖3 裝備巡回修理路徑規劃 由表2可以看出: 1) 從巡回修理組開始實施巡回修理至戰斗結束,共修復裝備26臺,獲得的裝備重要度總和為12.17,二次作戰時間為6 099 min,約101 h,對恢復部隊戰斗力提供了較有力的保障,間接證明了戰時巡回修理的重要性。 2) 調度時間均在12 s以內,滿足戰時裝備維修任務調度的實效性要求,同時也證明了所構模型和算法的可行性。 3) 在動態驅動策略的影響下,一共進行了6次調度,實現了待修裝備不斷出現情況下維修任務動態調整,其中前5次調度為遍歷型調度,第6次調度為非遍歷性調度;待修裝備20、28、29、30未納入最終的巡回修理任務規劃中,這主要是由于戰時修理時間的限制導致修理任務無法全部完成,反映了巡回修理的非遍歷性。 4) 在第105 min進行第2次調度時,待修裝備8納入巡回修理組3的修理計劃中,并安排在巡回修理組3的第3順位,但在第206 min進行第3次調度時,巡回修理組3還在修理第2順位的待修裝備7,待修裝備8參與重調度,并最終將其規劃到巡回修理組3的第4順位,并在第335 min得到修竣,類似的還有裝備9、16、20、22。這是動態調度的體現,反映了每個巡回修理組的任務序列對其自身而言并不一定是最優的,但是對于整體的巡回修理效益是最優的。這也間接證明了通過動態調度能夠更有利于全局的最優化,體現了動態調度的優勢。 5) 在第206 min進行第3次調度時,待修裝備9被納入巡回修理組3的第5修理順位,且計劃修復狀態為S1,但是在第4、5、6次重調度時,待修裝備9均參與了重調度,且最終在巡回修理組1的第7修理順位得到修復,且修復狀態為S2。這反映了在重調度時刻,會根據該時刻的全局信息對各巡回修理組的任務序列及各待修裝備的修復狀態進行動態調整,以實現全局的最優化,從側面反映了調度模型的合理性。 6) 前3次調度,待修裝備的修復狀態以S1為主,因為前期待修裝備較少,預計的修理時間相對較充裕,而μ2取值較大,將裝備修復至S1狀態能獲得更多的重要度,且前期修竣裝備參戰時間相對較長,更高的重要度有利于發揮作戰效能。后3次調度,待修裝備的修復狀態多為S2,因為此時參與調度的待修裝備數量多,且在戰斗中后期,μ3取值較大,希望能獲得更多裝備二次作戰時間,因此將待修裝備修復至S2狀態既能節約修理時間以便完成更多修理任務,又能迅速使其返回戰場獲得更多的二次作戰時間。 由圖3可以看出:巡回修理組1的規劃路徑中出現了折線3-6-5以及15-21-9-25-26,前者是因為裝備5相較于裝備6,修復到相同狀態的裝備重要度高且修理時間短,因此巡回修理組1在修竣裝備3后,舍棄較近的待修裝備6,而先修理重要度高且更易修復的待修裝備5,這滿足“先修重要裝備”以及“先修易修裝備”的戰時修理要求,也從側面反映了調度模型的合理性。而后者是因為該規劃是多次重調度的綜合結果,裝備15在第4次調度后得到修竣,裝備21、9是在第5次調度后得到修竣,而裝備25、26是在第6次調度才納入調度計劃并最終得到修竣,這也從側面反映了動態調度的核心是使整體修理效益最優化,而不是追求某一巡回修理組的修理效益最優。 合理高效的裝備巡回修理任務動態調度模型,可以為戰時保障指揮員的維修決策提供數學支撐,并能根據戰時不斷變化的維修需求作出及時有效的調整,大大降低了決策工作量和人為決策風險。筆者在提出巡回修理裝備維修任務動態調度軍事問題的基礎上,構建了維修任務的多目標動態調度模型,考慮待修裝備修復狀態的不確定性,引入待修裝備修理時間窗、非遍歷性以及修理能力的變化等約束條件,使模型更具現實意義并增強了模型的合理性,通過制定動態調度策略,實現了維修計劃的動態調整,設計了NSGA-Ⅱ改進遺傳算法求解了模型,并通過示例驗證了模型及算法的合理性。下一步將對定點修理中裝備維修任務動態調度問題展開研究。4 示例仿真與分析
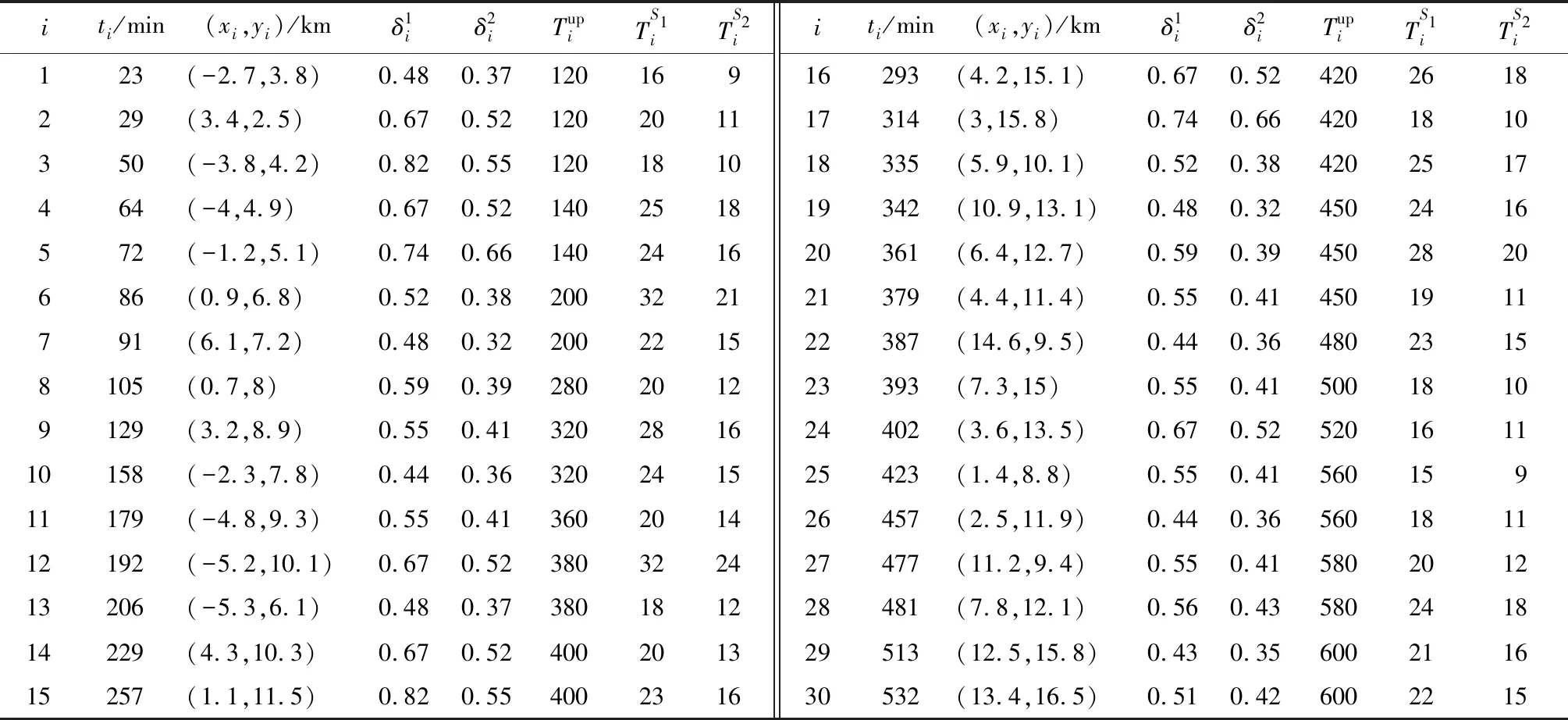
4.1 示例仿真
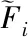

4.2 結果分析
5 結論

