小樣本下裝備平均修復時間的非統計估計模型
柯宏發, 祝冀魯, 孫云輝
(1. 航天工程大學航天保障系, 北京102206; 2. 北京亞美聯技術有限公司, 北京100080)
武器裝備維修性是指裝備在規定的條件下和規定的時間內,按規定的程序和方法進行維修時保持或恢復其規定狀態的能力[1]。對裝備維修性進行計算、驗證和評估[2],通常必須選用一系列定性和定量的維修性參數[3]。由于裝備平均修復時間直接影響裝備的可用性、戰備完好性,且與維修保障費用有關,因此成為描述裝備維修性的一個主要參數。
目前,對裝備平均修復時間進行估計與驗證的常用方法為:在自然故障或模擬故障條件下進行試驗,根據試驗數據分析判定維修性是否達到標準要求。這種驗證方法的理論基礎是經典數理統計學,需要假設樣本的概率分布特征,且需要較大的樣本量才能得到較高的估計精度。針對小樣本處理的Bayes方法[4-6]屬于一種概率統計方法,需要利用驗前信息并確定其概率分布形式,且非常依賴于驗前信息的融合正確性[7]。然而,隨著武器裝備的復雜化、網絡化、體系化發展,獲取較多裝備維修性驗證試驗樣本量的難度越來越大,成本也越來越高,亟需解決未知概率分布前提下小樣本數據的擴展生成、參數估計等技術難題。
在未知概率分布前提下,小樣本數據處理通常基于以下2種模式:1)基于不確定理論相關方法的直接估計方法[8],但這種方法難以給出參數估計的置信度;2)基于GM(1,1)模型等不確定理論相關方法的間接估計方法[9-13],如灰自助生成方法。均值GM(1,1)模型具有一定的適用范圍,對非指數增長或振蕩數據序列的均值GM(1,1)模型擬合誤差偏大,而裝備維修時間虛擬樣本原始數據序列往往呈現振蕩特征。對于非指數增長或振蕩數據序列,應優先選擇離散形態的原始差分、均值差分或離散GM(1,1)模型[14-15]。
筆者借鑒灰自助的樣本生成思想[10-13],提出通過離散GM(1,1)模型產生虛擬總體樣本的新方法,并通過未確知有理數[16-17]對總體樣本進行相應的點估計和區間估計,最后對算例進行了對比驗證。
1 小樣本數據的離散GM(1,1)模型生成
在武器裝備試驗活動中,由于試驗條件和費用的限制,很多測試指標得到的數據樣本量很小,其數據集合可以描述為
T′={x(t′),t′=1,2,…,N},
(1)
式中:x(t′)為第t′個測量數據;N為測量數據總數,通常情況下N∈[5,10]。對于此類小樣本指標數據,難以確定其概率分布特征,即使假設其服從正態分布,其參數估計的置信度也難以保證。灰色系統理論認為:這N個小樣本數據所攜帶的信息不足以確定測試指標的真實狀態和數量關系,但已經部分地反映了測試指標的真實狀態。通過“已知部分”推斷“未知部分”正是灰色系統技術與方法的優勢。
1.1 離散GM(1,1)模型
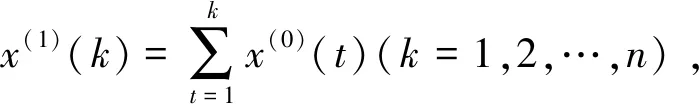
x(1)(k+1)=β1x(1)(k)+β2
(2)
為GM(1,1)模型的離散形式,簡稱離散GM(1,1)模型。式中:β1,β2均為待估計參數。
由最小二乘法(β1,β2)T=(BTB)-1BTY,得到β1、β2的值。由
(3)
(4)
并結合初始條件x(1)(0)=x(0)(1),即可得到離散GM(1,1)模型的時間響應序列
(5)
再將式(5)累減還原,得到X(0)的預測模型為
k=1,2,…,n。
(6)
在裝備維修時間的實際建模過程中,可以取初始序列為X(1),對其一階累減生成序列X(0)建立離散GM(1,1)模型,從而直接對X(1)進行模擬。
1.2 基于離散GM(1,1)模型的自助抽樣生成
根據GJB2072—94《維修性試驗與評定》[2]規定:維修作業樣本量按選取的試驗方法中的統計計算確定,也可選擇推薦樣本量。在此,將自助抽樣生成的樣本量選為推薦樣本量,即N+A=30。
自助抽樣生成原理的基本思路為:從原始數據集合X中等概率可放回地隨機抽取1個數據,記為x1(1),該抽取過程重復m次,得到第1個自助樣本,記為
X1={x1(1),x1(2),…,x1(m)}。
(7)
根據離散GM(1,1)模型的建模數據需求,確定m=5~8。為獲得自助樣本,將整體抽取過程連續重復A次,則會得到A個自助樣本,可記為
YA={X1,X2,…,Xi,…,XA},
(8)
式中:Xi={xi(1),xi(2),…,xi(m)}。
針對自助樣本Xi建立離散GM(1,1)模型,對其時間響應序列進行一次累減生成,即可得到自助樣本Xi中第m+1個預測值,記為
(9)
進而得到自助樣本集合,即新的裝備維修時間數據集合,為
X′={x(1),x(2),…,x(N),…,x(N+A)}。
(10)
式中:x(N+1),x(N+2),…,x(N+A)分別為A個自助樣本的離散GM(1,1)模型預測值。
上述自助抽樣生成流程如圖1所示。基于離散GM(1,1)模型的自助抽樣生成,是通過對原始數據序列的隨機抽樣挖掘,擬合生成了符合參數估計要求的數據信息,而未對原始數據序列的概率分布信息進行假設。然而,其中的自助樣本集合依然不能全面反映測試指標的真實狀態,在本質上還是“部分已知,部分未知”地實現對測試指標真實狀態的認知。與原始N個數據所表征的“部分已知,部分未知”相比,前者的“已知部分”要遠遠地多于后者,這也是自助抽樣挖掘的目的和作用。
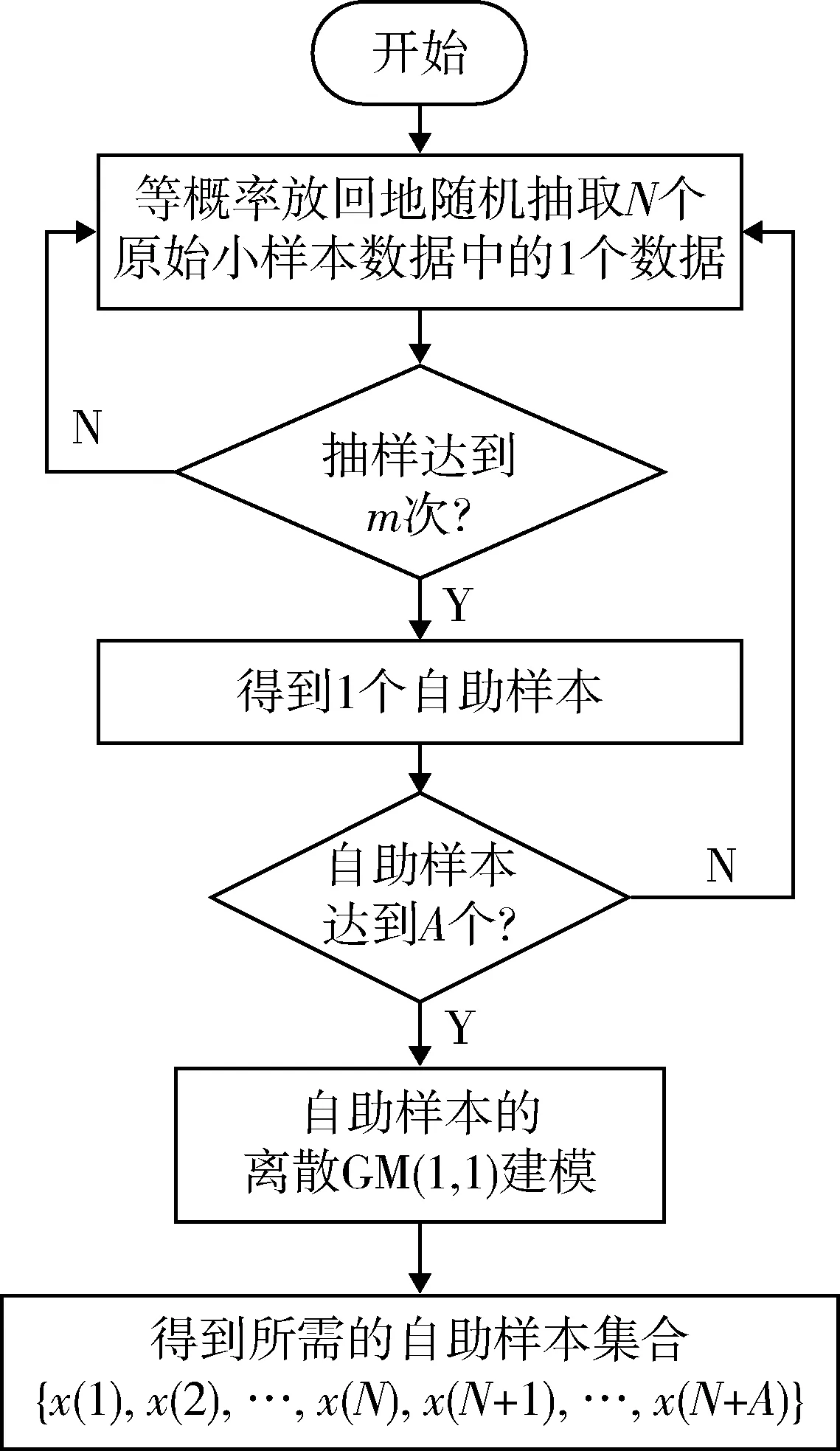
圖1 小樣本數據的自助抽樣生成流程
2 基于未確知有理數的參數估計
對自助樣本集合X′中N+A個數據的參數估計,若假設數據的分布特征,需要采用常規的統計方法進行點估計和參數估計,這就失去了自助抽樣挖掘的意義,且數據分布特征的合理性和正確性難以驗證。因此,不假設生成數據的概率分布規律,而直接引入未確知有理數方法進行參數估計。
2.1 未確知有理數的構造及優化
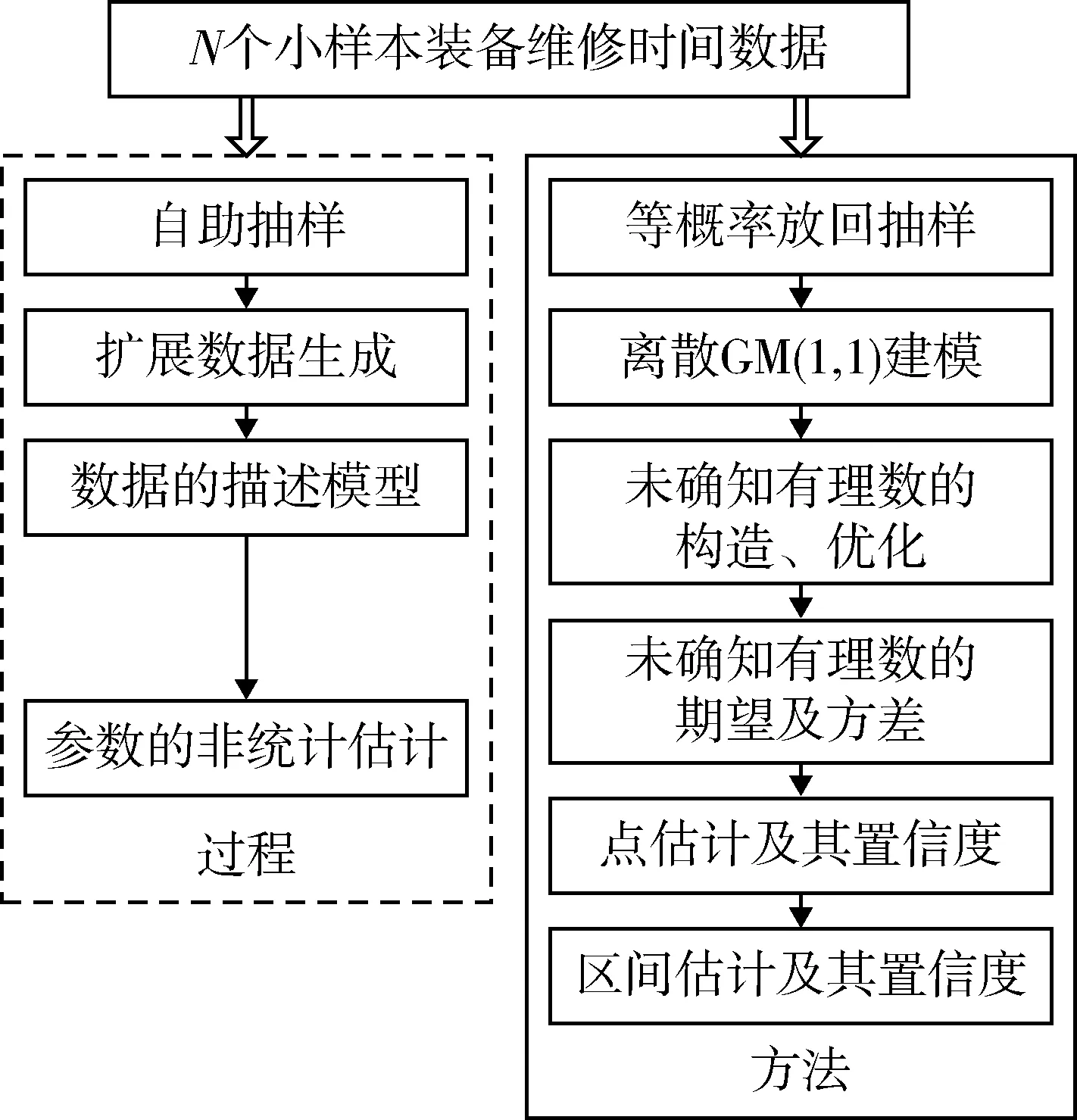
針對自助樣本集合X′,構造一個h(h 1) 記 a=min{x(1),x(2),…,x(N), x(N+1),…,x(N+A)}; (11) b=max{x(1),x(2),…,x(N), x(N+1),…,x(N+A)}。 (12) 2) 以小區間的中間值xj(a≤xj≤b,j=1,2,…,h)為中心、λ為控制半徑,確定一數據鄰域,統計N+A個數據在該鄰域出現的頻率,則可得到可信度分布密度函數表達式 (13) 3) 大多數情況下,對區間[a,b]進行2h個等值劃分,使得自助抽樣數據值xj(j=1,2,…,h)的鄰域控制半徑均相等,則可得到其表達式為 (14) 其可信度αj則用自助抽樣數據在xj為中心的控制鄰域內出現的頻率表示,即 (15) 4) 針對上述h階未確知有理數的可信度熵 (16) (17) 稱該h*階未確知有理數U為一階未確知有理數,其數學期望 (18) 式中: 用方差D(U)來描述未確知有理數U到E(U)的離散程度,即 D(U)=E(U-E(U))2= (19) 于是,自助樣本的點估計值為 (20) 其估計精度為 (21) 綜合未確知有理數期望的可信度,則定義自助樣本點估計的置信度 (22) 假設自助樣本的分布特征,可以用區間估計法給出樣本的取值范圍。一般假設自助樣本服從正態分布,常用標準正態分布上側β分位點如表1所示。 表1 常用標準正態分布上側β分位點表 給定置信水平1-β,從表1中查詢u(β/2),則給定置信水平下置信區間半長度 (23) 針對自助抽樣挖掘生成的N+A個數據,假設有q個數據位于上述置信區間之外,同時綜合估計區間的置信水平,則定義自助樣本在上述區間估計的置信度 (24) 需要注意置信水平和置信度2個概念的聯系與區別。本文對裝備維修時間的非統計估計分為自助抽樣生成、參數描述和參數估計等過程,置信水平反映了正態分布假設條件下區間估計的可靠性,覆蓋了參數估計過程;而點估計和區間估計的置信度則覆蓋了裝備維修時間的非統計估計全過程,置信水平對區間估計置信度有一定的貢獻率。 基于離散GM(1,1)模型的自助抽樣生成和未確知有理數的裝備維修時間非統計估計,是在小樣本自助抽樣生成、參數描述與估計等過程中,應用離散GM(1,1)建模技術,基于未確知有理數的點估計和區間估計等方法論的一種分析方法,其過程和方法論框架如圖2所示。 圖2 裝備維修時間的非統計估計模型的過程和方法論框架 為驗證本文算法的有效性,采用GJB 2072—94《維修性試驗與評定》[2]D1.5中的裝備維修時間數據,即26,14,21,30,70,69,20,21,18,65,16,34,26,16,40,28,42,33,19,19,43,54,12,18,13,26,10,50,21,31,42,30,46,24,總計34個。將自助樣本的非統計估計結果與原始34個數據樣本的非統計估計結果、GJB2072-94建議估計模型的估計結果進行對比驗證。 利用本文非統計估計算法對D1.5中34個裝備維修時間原始數據進行處理,其最佳4階未確知有理數為[[10,70],φ(x)],其中 對原始34個數據,每間隔2個數據取為自助抽樣對象,抽樣生成小樣本數據;而取小樣本數據的前10個作為驗證數據,即26,30,20,65,26,28,19,54,13,50。對這10個小樣本數據進行等概率可放回地隨機抽樣,重復抽取m=6次視為得到1個自助樣本,總共需要得到A=20個自助樣本。 分別針對這20個自助樣本進行離散GM(1,1)建模,取每個模型的一步預測值,從而得到自助樣本集合為X′={26,30,20,65,26,28,19,54,13,50,22.1,13.5,27.5,51.2,24.8,23.4,26.5,34.2,65.8,41.1,32.7,46.0,29.0,16.5,12.1,69.0,51.5,19.5,17.8,29.6}。上述自助樣本的最大值為69.0,最小值為12.1。構造h階未確知有理數,其對應的可信度熵如表2所示。 表2 不同階數未確知有理數的可信度熵 由表2可以看出:可信度熵最大值為0.137 6,其對應的最優未確知有理數階數h*=4,則本算例構造的4階未確知有理數為[[12.1,69.0],φ(x)],其中 假設置信水平為0.95,則β=0.05,計算給定置信水平下的置信區間半長度ε=14.17,則得到裝備維修時間的區間估計[18.79,47.13],這時有q=12個點位于上述區間之外,區間估計的置信度p2=57.0%。 本算例中,裝備維修時間的概率分布和方差都是未知的。依據GJB2072—94《維修性試驗與評定》[2]D2中試驗B的估計模型,有: 結合4.1、4.2節可知:針對自助樣本、原始數據樣本,基于本文非統計估計算法的點估計和區間估計結果均較為接近,且估計置信度也很接近,說明基于離散GM(1,1)模型的樣本數據挖掘生成方法有效可行。 結合4.1-4.3節,對原始34個數據樣本和自助樣本分別進行點估計及位于估計區間之外的點數比較,如表3、4所示。 表3 點估計比較 表4 估計區間之外的樣本點數比較 由表3可知:與GJB2072—94[2]建議估計模型的估計結果相比,原始數據樣本的非統計估計模型點估計相對誤差為1.15%,自助樣本估計相對誤差為0.39%,這2個數據樣本的點估計結果相對誤差均較小,而自助樣本的誤差更小。 由表4可知:同一置信水平下,估計區間覆蓋了數據樣本的個數,說明本文提出的非統計估計模型要遠遠好于GJB2072—94[2]估計模型。 上述結果表明:本文提出的小樣本裝備平均修復時間非統計估計模型有效可行。 針對裝備平均修復時間的小樣本參數估計問題,提出了一種基于離散GM(1,1)模型和未確知有理數的新方法,構建了裝備平均修復時間的點估計和區間估計模型,并與GJB2072—94建議的估計模型進行對比,驗證了其有效性。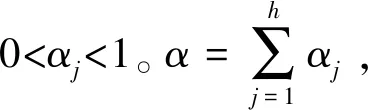
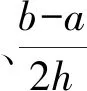
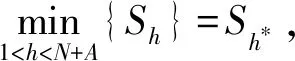
2.2 基于未確知有理數的點估計
2.3 基于未確知有理數的區間估計

3 非統計估計模型的過程和方法框架
4 裝備平均修復時間的非統計估計算例
4.1 原始數據非統計估計結果

4.2 自助樣本的非統計估計結果

4.3 GJB2072—94建議模型的估計結果
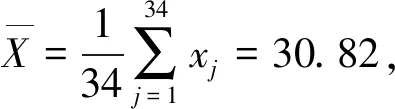
4.4 對比分析


5 結論

