一種損傷準則在差厚板拉伸成形中的應用

余月紅，付秀娟，楊 帥，于 歌，趙 嚴

武漢工程大學材料科學與工程學院，湖北 武漢 430205

差厚板做為一種輕量化材料，在能有效保持安全性能、舒適性的同時降低燃料的消耗，因此越來越受到人們的關注［1-4］。然而在差厚板成形過程中板料發生的起皺、破裂等斷裂缺陷直接影響零部件的質量，如何預測和避免發生這些缺陷對于指導生產實踐有著重要意義［5］。國內外學者從成形極限、韌性損傷準則等方面建立了各種預測板料破裂的準則，并采用實驗和模擬結合的方法驗證了所建立準則的準確性［6-8］。李云［9］基于Lemaitre理論，采用混合法對實驗和模擬結果進行分析，建立了適用于高強鋼差厚板熱成形的韌性斷裂準則。黃建科［10］將新建立的韌性斷裂準則應用于金屬板料成形中斷裂預測，并進行沖壓試驗，結果表明所建立的韌性斷裂準則比成形極限圖能夠更好預測非線性變形路徑下的板料沖壓過程中的破裂現象。楊信［11］以連續損傷力學為基礎，通過Abaqus軟件對盒形件沖壓進行模擬，建立了韌性斷裂準則并得到了差厚板盒形件的沖壓成形極限預測值。

然而國內外學者［12-16］大多數都是對等厚板進行研究，對于差厚板斷裂成形行為研究較少，本文提出采用單向拉伸實驗與反復加載卸載實驗相結合的方法來研究差厚板拉伸斷裂行為，首先通過單向拉伸實驗獲得了差厚板基本的力學性能參數，分析了拉伸中塑性行為變化，然后結合反復加載卸載實驗得到了差厚板斷裂準則，建立了損傷變量與應變之間的非線性關系式，并采用實驗與數值模擬結合的方法來驗證所建立準則的準確性。

1 實驗部分

實驗材料為Cr340差厚板，化學成分：w（C）=0.077%，w（Mn）=0.429%，w（Si）=0.341%。還含有少量的S、Al等元素。差厚板由厚度2 mm的厚區、過渡區和厚度1 mm的薄區組成，板材沿拉伸方向的截面形狀如圖1所示。根據實驗標準ASTM，差厚板不同厚度區域反復加載卸載試樣尺寸與單向拉伸試樣尺寸相同，如圖2所示。實驗設備為INSTRON電子萬能拉伸試驗機，拉伸速度為2 mm/min。

2 結果與討論

2.1 單向拉伸實驗

應用單向拉伸實驗得到的材料力學性能參數如表1所示。拉伸結果如圖3所示，差厚板不同區域拉伸真應力-應變曲線如圖4所示。從表1可以看出，三者的楊氏模量相近，屈服強度和抗拉強度過渡區最小，板料的屈服強度是彈性變形和塑性變形的分界點，屈服強度越小，表明板料越容易發生塑性變形。差厚板過渡區的屈強比為0.76，與薄區、厚區相比其最小，而屈強比是衡量板料沖壓成形性的間接指標，小的屈強比幾乎對所有的沖壓成型都是有利的，屈強比小表明板料容易產生塑性變形而不易產生拉伸斷裂，塑性變形空間大，成形性能好。

表1 軋制差厚板力學性能參數Tab.1 Mechanical property parameters of tailor rolled blank

圖3 差厚板不同區域試樣拉伸結果Fig.3 Stretching results of tailor rolled blank in different zones

圖3和圖4表明，差厚板試樣在單向拉伸力的作用下，經過彈塑性變化發生斷裂，其斷裂位置在過渡區內靠近薄區處，而等厚區其斷裂位置位于平行部分中間處。這是由于差厚板厚度的不均勻性及加工過程導致的。一方面，在拉伸過程中，相同的拉伸力，截面積越小越容易產生斷裂，另一方面，由于差厚板是軋制形成的，在加工過程中會產生微觀上的空洞等缺陷，導致在拉伸過程中，斷裂易在缺陷處發生。

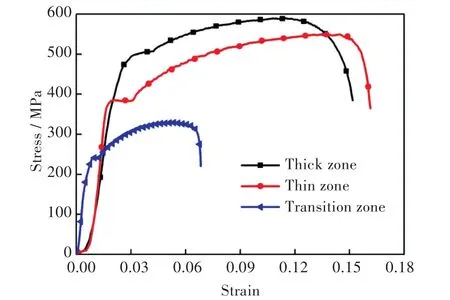
圖4 差厚板不同厚度區域試樣的真應力-應變曲線Fig.4 True stress-strain curves of tailor rolled blank in different zones

2.2 反復加載卸載實驗

在拉伸相同距離后以相同的速率進行卸載，根據實驗結果計算出彈性模量和損傷變量，計算方法如式（1）和式（2）所示，并獲得不同厚度損傷變量、彈性模量與應變的關系，如圖5所示。

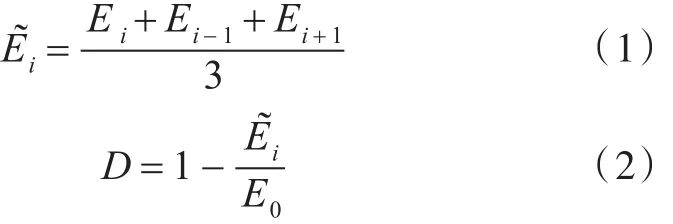
經過反復加載卸載實驗得到不同厚度區域板料斷裂時的應變εc、未損傷材料的彈性模量E0及斷裂時的損傷變量Dc如表2所示，不同厚度區域板料在拉伸初始階段，彈性模量E下降趨勢較大，在接近斷裂時，下降逐漸變緩慢。從圖5可以看出，損傷變量隨應變先上升得較快，后較慢，采用線性函數和非線性函數對其進行擬合，非線性擬合度大于線性擬合度，故損傷變量與應變之間的關系更適合于非線性擬合，擬合結果見式（3）～式（5）。

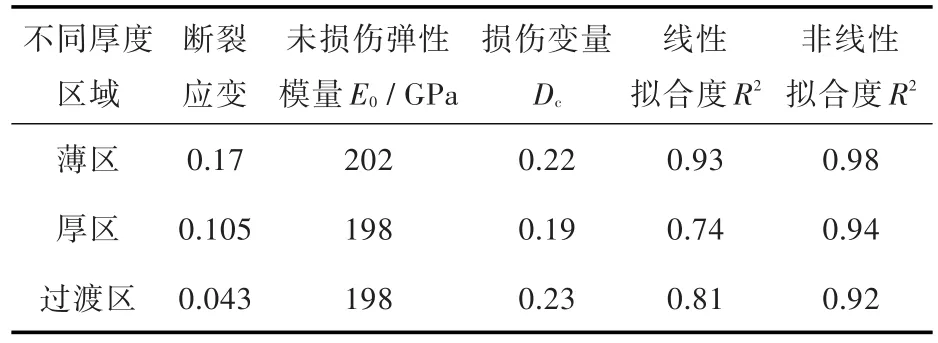
表2 差厚板不同厚度區域加載卸載結果Tab.2 Results of loading and unloading of tailor rolled blank in different zones

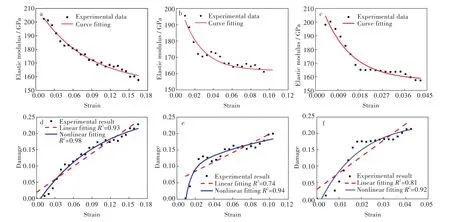
圖5 不同厚度區域彈性模量-應變關系：（a）薄區，（b）厚區，（c）過渡區；不同厚度區域損傷變量-應變關系：（d）薄區，（e）厚區，（f）過渡區Fig.5 Relationships between elastic modulus and strain of specimens in different zones：（a）thin zone，（b）thick zone，（c）transition zone；Relationships between damage and strain of specimens in different zones：（d）thin zone，（e）thick zone，（f）transition zone

其中，式（3）為1 mm薄區損傷變量與應變關系，式（4）為2 mm厚區損傷變量與應變關系，式（5）為過渡區損傷變量與應變關系。

2.3 數值模擬結果

基于Abaqus/cae平臺分別創建1 mm和2 mm的等厚區拉伸模型，同時創建厚度連續變化的過渡區板料的拉伸模型，并采用八節點線性六面體單元，縮減積分，沙漏控制（C3D8R）對其進行網格劃分，并將實驗中獲得的材料參數賦予給對應厚度的單元，一端固定，另一端以與實驗相同的速率進行仿真模擬，差厚板單向拉伸仿真模型如圖6所示。圖7為嵌入損傷準則的差厚板拉伸后應變分布云圖，從圖7中可以看出，塑性變形集中于差厚板薄區內，厚區幾乎不變形，其斷裂位置位于試樣鄰近薄區的平行部分，且是發生明顯緊縮后斷裂，這與拉伸實驗結果相吻合，表明損傷準則是較準確的。圖8是實驗和模擬的力與位移關系曲線，從圖8可以看出，兩者彈性模量較接近，發生緊縮位置相吻合，實驗與模擬相比，兩者基本吻合，再次驗證了損傷準則的準確性。

圖6 單向拉伸試樣有限元模型Fig.6 Finite element model of uniaxial tensile specimen

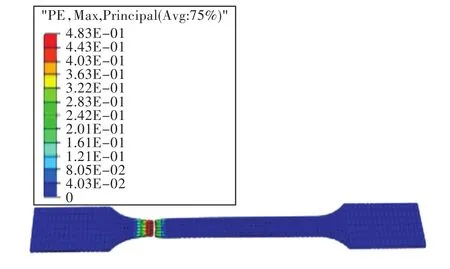
圖7 差厚板單向拉伸應變分布云圖Fig.7 Strain distribution contours of uniaxial tensile specimen

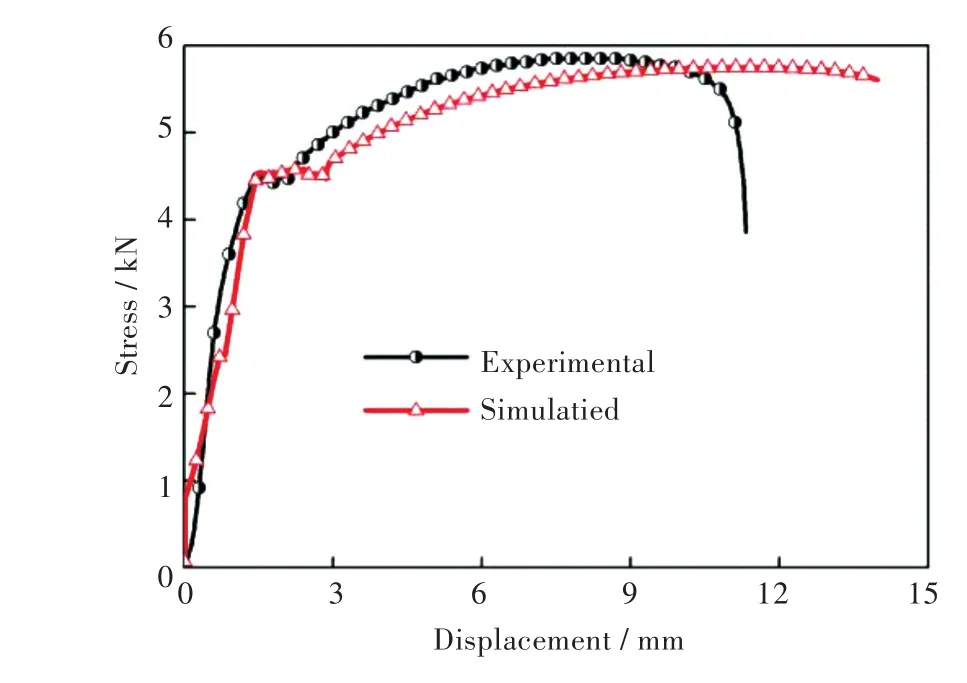
圖8 實驗與模擬的力-位移曲線Fig.8 Curves of experimental and simulated stress-displacement

3 結 語

本文通過單向拉伸實驗建立了差厚板厚度真應力-應變關系曲線，結合反復加載卸載實驗建立了差厚板非線性損傷準則，并將其運用于Abaqus有限元軟件中，通過實驗與模擬結合的方法，得到以下結論：

1）差厚板單向拉伸中損傷變量與應變之間呈現非線性關系，且損傷變量隨應變增加呈現出先增加得較快后較慢的趨勢。

2）將實驗得到的損傷關系式嵌入Abaqus軟件中對差厚板進行模擬實驗，模擬結果表明塑性變形主要集中于鄰近薄區的厚區過渡區，斷裂位置與實驗相吻合，驗證了損傷關系的準確性。