基于ARIMA和GM模型的青島港貨物吞吐量預測研究

韓以倫，徐新新

(山東科技大學 交通學院，青島 266590)

港口是一帶一路建設的重要樞紐和重要支點，是全球貿易的流通載體，是城市成長的主要驅動力，并日益成為區域經濟發展的核心。沿海城市和港口在“一帶一路”建設的推動下不斷發展，青島港作為“21世紀海上絲綢之路”的重要節點[1]，應在新形勢下抓住港口轉型升級的有利契機。青島港只有認清現狀，分析面臨的機遇與挑戰，制定針對性的策略，才能承擔新的歷史使命，促進港口的蓬勃發展。對港口的貨物吞吐量進行預測和分析是各港口在發展過程中需要探索的重要內容，它對合理進行港口發展規劃并制定具有針對性的港口發展戰略具有重要作用。

目前港口貨物吞吐量的預測模型有很多，比較常見的模型包括指數平滑模型、時間序列模型、灰色預測模型及線性回歸模型等，也有學者運用馬爾科夫區間預測模型、神經網絡模型、模擬植物生長模型等來對港口貨物吞吐量進行預測。各種模型在港口吞吐量的預測適用范圍存在一定的差異，對不同的數據波動程度的預測精度也存在一定的差異。由于影響貨物吞吐量的因素較多，在量化影響因素方面具有一定難度，因此采取多元回歸分析和時間序列來科學合理地選取影響因素，最后運用灰色理論來預測港口貨物吞吐量。

1 模型簡介

1.1 ARIMA模型

ARIMA的基本思想是[2]：所預測對象的觀測值是按照時間順序取得隨機數據，這些觀測值之間具有一定的依賴性，而這種依賴關系是某變量的過去變動規律，利用這個規律來建立一定的數學模型，這個模型一旦被識別后就可以從時間序列的過去值及現在值來預測未來值。所處理的ARIMA模型若被接受就可以應用于時間序列之中從前樣本數據、現期數據對之后的數據進行預測。基于時間序列理論，能夠預測出一系列相關的指標。時間序列的建模屬于動態經濟學的范疇，可以應用在非常廣闊的領域內，例如應用于企業對未來發展進行預測。

ARIMA模型，全稱為自回歸積分滑動平均模型。包括移動平均過程(MA)、自回歸過程(AR)、自回歸移動平均過程(ARMA)以及ARIMA過程。其中AR是自回歸，p為自回歸項；MA為移動平均，q為移動平均項數，d為時間序列成為平穩時所做的差分次數。時間序列建模步驟主要包括：首先，對獲取的序列數據繪圖，觀察其是否為平穩時間序列；若為平穩序列，不需進行數據處理，倘若為非平穩序列，則應進行d階差分，使其化為平穩序列，ARIMA(p,d,q)模型中的d便是差分階數；其次，求平穩序列的自相關系數ACF和偏自相關系數PACF，并對其自相關圖和偏自相關圖進行分析，得到p和階q，從而得到ARIMA模型；最后，對所得的ARIMA模型進行檢驗。

1.2 灰色預測模型

灰色預測模型[3]簡稱GM預測模型，是通過少量的、不完全的信息建立數學模型并做出預測的一種預測方法，在工業、農業等眾多領域得到了廣泛應用，成功地解決了大量的實際問題。灰色預測的序列數據從表面上看是隨機的、無章的，但其實質卻是有序、有界的，數據之間存在一定的潛在規律，根據這種規律，通過數據處理，進一步發現與掌握規律，建立數學模型對系統未來實現科學的定量預測。

灰色系統理論建模的目的是依據社會、經濟和技術等系統的行為特征數據找出因素本身或者因素之間的數學關系，從而確定系統的發展趨勢。灰色系統理論的建模實際上是對生成數列的建模，而一般數學建模方法則用原始的數列直接建模。灰色預測的核心模型包括GM(1,1)模型和灰色Verhulst模型，Verhulst模型是在Malthusian線性模型的基礎上加入制約項后演變成的非線性模型,其模型建立過程與GM(1,1)模型相似[4]。建模步驟主要包括：首先，需運用累加生成、累減生成等方法對原始數據進行預處理，使離散的數據顯現出規律性；其次，對生成的序列建立灰色微分方程，并利用最小二乘法求出相應參數，建立時間響應函數；最后還原模型，進行預測和檢驗。

2 青島港貨物吞吐量預測過程

青島港位于山東半島南岸的膠州灣內，由四大港區組成，分別是青島老港區、黃島油港區、前灣新港區和董家口港區。青島港是山東沿海港口群的核心，是國家沿海的主要港口，因地理位置優越性成為中韓自貿區的重要支撐，是“一帶一路”的重要節點城市之一，在眾多國家戰略中擔任重要角色[5]。青島港2016年吞吐量實現歷史性突破，達到5.003 6億t，同比增長3.3%，集裝箱突破1800萬標準箱，集裝箱裝卸效率和鐵礦石接卸效率繼續保持世界第一。

對青島港貨物吞吐量進行預測，依據一定的合理性將所預測的數據作為未來青島港的運輸需求量和港口承載力，并對其進行分析。首先，青島市幾乎全部進出口貿易活動都是由港口物流運輸來承載，因此它與吞吐量具有較大的相關性，讓其代表青島港口運輸的需求量，作為因變量Y，選取影響進出口貿易額的六個因素作為自變量X，建立多元回歸方程，處理數據之后建立“ARIMA模型”。其次，再利用灰色預測模型來預測青島港未來5 a的港口貨物吞吐量，用以代表港口承載力。最后，對預測結果的數據進行分析，發現其現有的物流發展空間與經濟發展不大相符。期望青島港借助“一帶一路”戰略東風，擴大港口規模、完善基礎設施建設，調整產業結構，為港口物流發展戰略的制定提供參考依據。

2.1 吞吐量相關數據的提取

影響港口吞吐量的因素眾多，包括：經濟環境、經營管理能力、政策環境、自然地理條件、信息化水平、服務水平以及創新能力等，港口與城市之間的經濟聯系密不可分，本文選取能體現港口規模的顯性因素指標作為變量[6]。文中采用多元回歸模型分析各影響因素，包括青島市的對外貿易進出口總額、市生產總值、固定資產投資額、第二產業產值、第三產業產值、實際利用外資以及水運運輸量，對對外貿易進出口總額和實際利用外資的單位美元統一化為人民幣元，借助于Eviews軟件，最終提取了青島市的固定資產投資、第二產業產值以及水運運輸量三個指標。最后經過多方面的綜合比較和檢驗，確以外貿易進出口總額為因變量的青島港貨物吞吐量預測模型。表1為1997年～2017年青島市港口吞吐量的相關數據。

表1 1997年～2017年青島市港口吞吐量相關數據Tab. 1 Qingdao Port throughput related data from 1997 to 2017

數據來源：青島市統計年鑒(1997年～2017年)。

2.2 多元回歸分析

將青島市的對外貿易進出口總額作為因變量Y，青島市生產總值、固定資產投資額、第二產業產值、第三產業產值、實際利用外資以及水運運輸量作為六個自變量，分別設為X1、X2、X3、X4、X5、X6。對這些變量建立多元回歸方程式，從而分析青島市外貿易進出口總額。

設多元回歸方程為

Y=β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+C

(1)

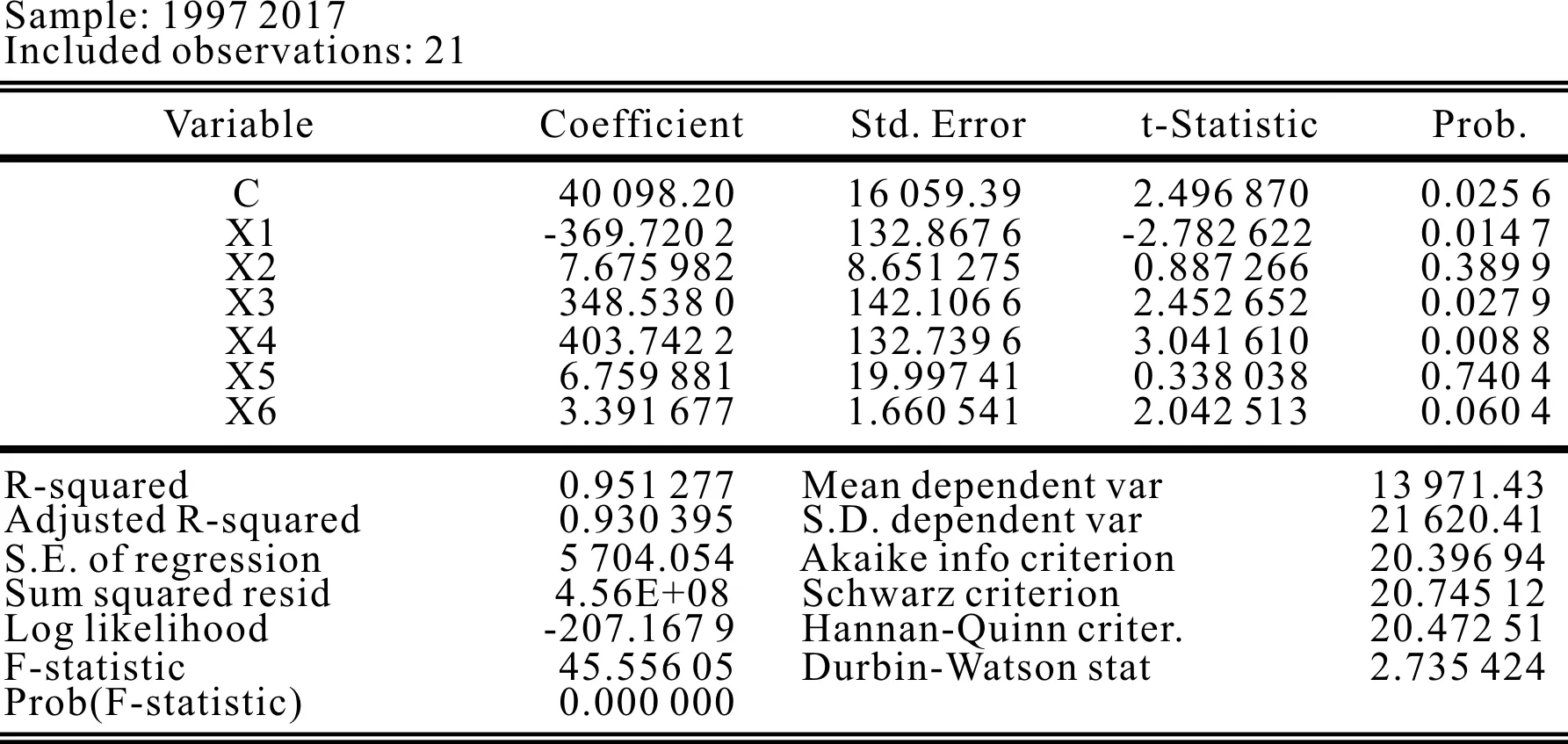
圖1 最小二乘法估計圖Fig.1 The least square estimation graph

Y=27.349 68X2-34.206 66X3+5.897 021X6+1 547.147

圖2 一元回歸分析圖Fig.2 Univariate regression analysis圖3 二元回歸分析圖Fig.3 Binary regression analysis

圖4 三元回歸分析圖Fig.4 Triple regression analysis圖5 四元回歸分析圖Fig.5 Quadratic regression analysis

2.3 ARIMA模型的預測

(1)平穩性檢驗。

運用Eviews軟件對X2、X3、X6三個自變量進行數據處理[8]，根據所得的自相關和偏相關圖可分析出X6只需將初始序列進行“一階差分”就可以顯著平穩，為一階單整；X2、X3需將進行“二階差分”才可以顯著平穩。從圖6、圖7和圖8中的一階和二階差分后的ADF檢驗結果圖可以觀察到，X2、X3、X6的t統計量分別是：-4.031 895、-3.981 138、-4.179 184，在1%、5%、10%的顯著性水平下都能拒絕原假設，接受不存在單位根的檢驗，p值都顯著小于0.05，所以可以確定X2、X3的二階單整和X6的一階單整序列可以用于ARIMA模型的構建[9]。

圖6 X2二階差分ADF檢驗圖Fig.6 X2 second-order differential ADF test 圖7 X3二階差分ADF檢驗圖Fig.7 X3 second-order differential ADF test 圖8 X6一階差分ADF檢驗圖Fig8 X6 first-order differential ADF test

(2)模型預測。

觀察X2的自相關和偏自相關圖顯示，自相關系數在3階超出兩倍標準差外，偏自相關1階截尾，所以可建立ARIMA((1，2，3),1，1)的模型，經過比較其調整后的R2，ARIMA(1，2，1)為最大，模型最優，其參數估計如圖9所示，用此模型對X2的2018～2022年的值進行預測。

從X3的自相關和偏自相關圖可以觀察到，自相關系數在滯后三階歸于零，偏自相關滯后一階四階歸于零，在ARIMA(p，d，q)模型中，p值取1,2,3，q取1,2,3,4，因此得到模型ARIMA((1,2,3)，2，(1,2,3,4))，經過比較其調整后的R2，ARIMA(2，2，4)為最大，模型最優，其參數估計如圖10所示，用此模型對X3的2018～2022年的值進行預測。

圖9 X2的模型參數估計圖Fig.9 Model parameter estimation of X2圖10 X3的模型參數估計圖Fig.10 Model parameter estimation of X3圖11 X6的模型參數估計圖Fig.11 Model parameter estimation of X6

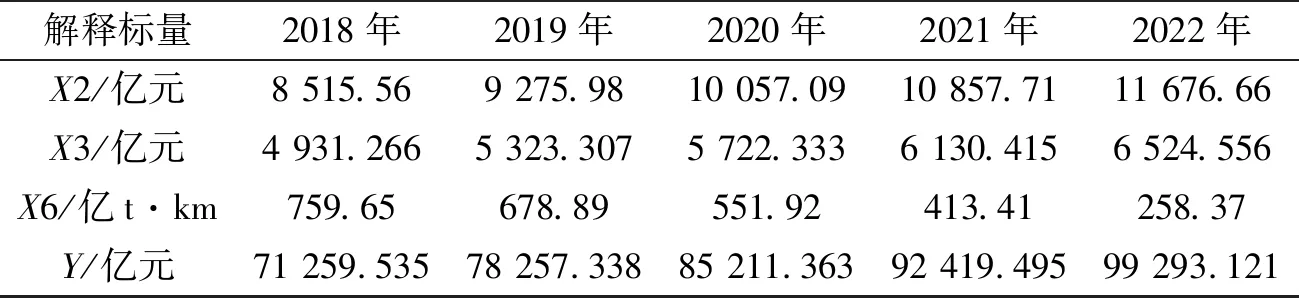
表2 X2、X3、X6及Y序列預測結果表Tab.2 X2, X3, X6 and Y sequence prediction results

觀察X6的自相關和偏自相關圖顯示，自相關系數在2階超出兩倍標準差外，偏自相關4階截尾，所以可建立ARIMA((1，2)，1，(1,2,3,4))的模型，經過比較其調整后的R2，ARIMA(2，1，4)為最大，模型最優，其參數估計如圖11所示，用此模型對X6的2018～2022年的值進行預測。

運用ARIMA模型對X2、X3、X6三個序列近五年的數據進行預測，并帶入多元回歸方程：Y=27.349 68X2-34.206 66X3+5.897 021X6+1 547.147，預測數據如表2所示。

2.4 GM模型在吞吐量預測中的應用

圖12 青島港貨物吞吐量的曲線圖Fig.12 Qingdao Port cargo throughput curve

觀察圖12可以發現，青島港近20 a的貨物吞吐量的變化趨勢是呈現指數遞增的，這種趨勢與GM預測模型的還原時間響應函數的指數形式是一致的，因此利用灰色預測模型對青島港貨物吞吐量進行預測具有一定的可行性[10]。利用灰色模型中的GM(1,1)和Verhulst模型相組合對青島港貨物吞吐量進行實踐預測的具體步驟如下：

(1)對原序列X0做一次累加或累減生成。

由1997～2017年青島港口吞吐量相關數據表可知，貨物吞吐量原始序列為：

X0=(6 943；7 043.5；7 282；8 660.71；10 422.9；12 251.6；14 090；16 265；18 678；22 415；26 502; 30 029；31 668.4；35 012；37 971；41 464.82；45 613；47 782；45 895；50 036；51 786)

GM(1,1)和Verhulst模型分別經過一次累加和一次累減減生成X1和X2：

X1=(6 943；13 986.5；21 268.5；29 929.21；40 352.11；52 603.71；66 693.71；82 958.71；101 636.71；124 051.71；150 553.71；180 582.71；212 251.11；247 263.11；285 234.11；326 698.93；372 311.93；420 093.93；465 988.93；516 024.93；567 810.93)

X2=(100.5；238.5；1 378.7；1 762.19；1 828.7；1 838.4；2 175；2 413；3 737；4 087；3 527；1 639.4；3 343.6；2 959；3 493.82；4 148.18；2 169；-1 887；4 141；1 750)

(2)對X0進行準光滑性的檢驗。

GM(1,1)和Verhulst模型經過計算得出光滑比為：

p(k)=( 1.014 5；0.520 6；0.407 2；0.348 3；0.303 6；0.267 9；0.243 9；0.225 1；0.220 5；0.213 6；0.199 5；0.175 4；0.165 0；0.153 6；0.145 4；0.139 6；0.128 3；0.109 2；0.107 4 ；0.100 4)；

可知，當k>2時可以滿足準光滑條件。

(3)生成緊鄰均值序列。

對序列X1和X2進行緊鄰均值生成，經過計算得：

Z1=(10 460；17 630；25 600；35 140；46 480；59 650；74 830；92 300；11 280；137 300；165 570；196 420；229 760；266 250；305 970；349 510；396 200；443 040；491 010；541 920)

Z2=(6 993.25；7 162.75；7 971.355；9 541.805；11 337.25；13 170.8；15 177.5；17 471.5；20 546.5；24 458.5；28 265.5；30 848.7；33 340.2；36 491.5；39 717.91；43 538.91；46 697.5；46 838.5；47 965.5；50 911)

(4)建立灰色微分方程。

GM(1,1)通過最小二乘法求得參數a，b，即：a=-0.089 529 755 148 312 7；b=10 147.019 625 676 0。

Verhulst模型通過最小二乘法求得參數a，b，即：a=-0.207 208 928 497 967；b=-3.425 921 010 981 54e-06。

(5)求時間響應函數并得到還原模型。

GM(1,1)模型：

時間響應函數為：X1(k+1) =(X0(1)+113 336.841)e0.089 529 755 148 312 7k-113 336.841

還原時間響應函數：X0(k+1)=(1-e0.089 529 755 148 312 7k)(X0(1)+113 336.841)e0.089 529 755 148 312 7k

Verhulst模型：

時間響應函數為：X1(k+1) =(X0(1)+94 326.816)e-0.207 208 928 497 967k-94 326.816

還原時間響應函數：X0(k+1)=(1-e-0.207 208 928 497 967k)(X0(1)+943 26.816)e-0.207 208 928 497 967k

(6)預測貨物吞吐量。

對預測模型進行檢驗：GM(1,1)和Verhulst模型的絕對誤差標準差分別為為2 260.571和1 236.841，方差比分別為c=0.145 12<0.35和c=0.126 373 7<0.35，依據灰色模型的精度評定要求可知c<0.35時精度等級為一級，因此兩種模型預測效果較好。

通過還原時間響應函數得到還原值及預測值，預測值見表3。

(7)灰色組合模型預測貨物吞吐量。

在此采用方差倒數法來確定GM(1,1)和Verhulst模型在組合中所占的權重即，對誤差平方和小的模型賦以高權重，求得ω1=0.127，ω2=0.873。三種模型的港口吞吐量預測值及預測誤差如表3所示，可以發現灰色組合模型的平均預測誤差要小于兩個單一模型，所以最終的吞吐量預測采用灰色組合模型。

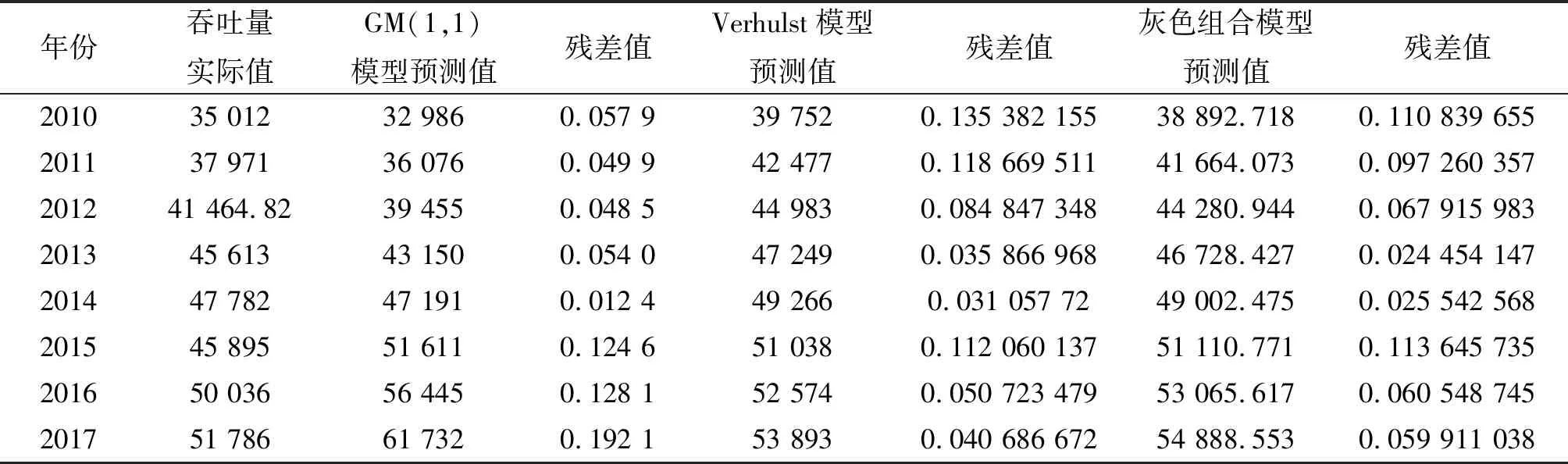
表3 預測結果與精度對比表Tab.3 Comparison of forecast results and precision

圖13為三種預測模型的吞吐量預測擬合曲線圖，可以看出GM(1,1)模型前期預測值偏小，后期預測值偏大，吞吐量增速過快；而灰色Verhulst模型前期預測值稍大，后期增速稍慢；灰色組合預測模型克服了兩種單一模型的缺點，總體擬合效果較好，優于單一模型。表4為2018～2022年青島港貨物吞吐量預測值。

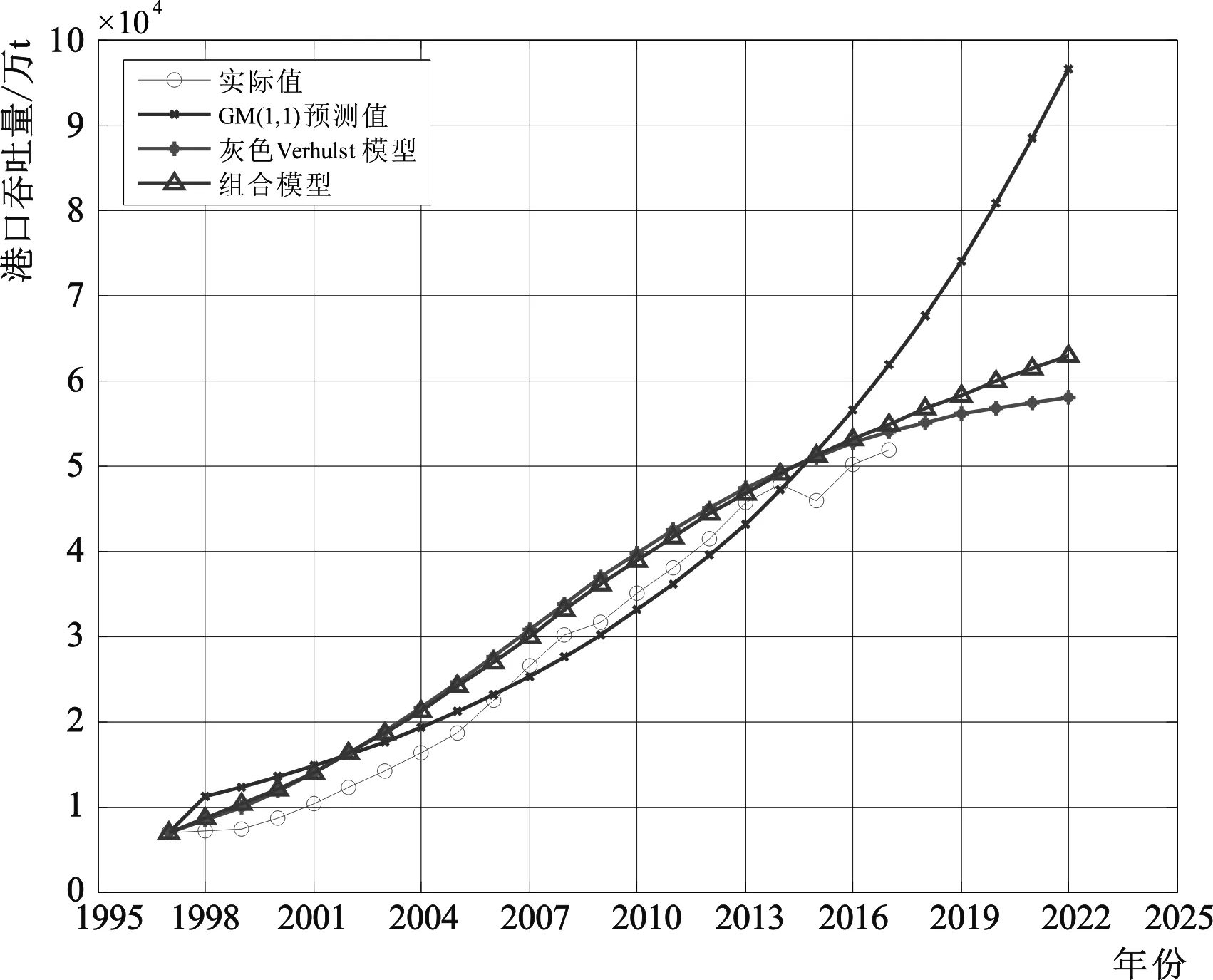
圖13 模型預測曲線擬合圖Fig.13 Curve fitting of model prediction

2018年2019年2020年2021年2022年56 602.37358 232.12559 803.61961 342.04662 872.74

3 青島港吞吐量預測結果分析

通過對青島市近20 a的進出口貿易總額與貨物吞吐量進行對比分析，發現盡管在總量變化上有一定差異，但兩者增速趨勢大致相符，相關性較大。對青島港的運輸需求量進行分析，青島市進出口貿易總額的預測采用了多元回歸模型和ARIMA模型相結合的方法。對其單位進行了統一化處理為單位/人民幣元，從預測結果可以看出，預測數據雖然存在一定差異，但與實際值相比誤差較小，在合理范圍內，接受預測結果。從剔除三個自變量后的多元回歸方程來看，方程中各自變量的系數代表了各自對因變量的影響狀況，可以看出：青島市固定資產投資(X2)對進出口貿易影響最大，它以貨幣量表示對港口設施投建資產，對港口運輸的發展提供了堅實的保證；青島市第二產業產值(X3)以及水運運輸量(X6)對青島市港口運輸需求量有必然影響。由2018～2022年的進出口貿易總額的預測值可以推斷出青島市進出口貿易經濟狀態有較大的發展潛力，能為青島港港口運輸提供相當的需求市場保證。

通過對近20 a的青島市國內生產總值發展趨勢來看，總量呈級數增長，增速變化平緩波動較小，因此為港口吞吐量的增長提供了堅實的保障。對青島港的港口承載力進行分析，通過對青島港近20 a的貨物吞吐量進行灰色預測，可以從預測值中看出港口吞吐量不斷增加，增長速度呈現指數型，預測結果比較可信。青島港在現行經濟增長處于“三期疊加”時期，結構性矛盾突出的情況下，實際吞吐量仍保持較快增長。在《山東省沿海港口布局規劃》中明確提到貨物吞吐量在2020年和2030年的預達成目標分別為5.4億～5.6億t以及7億～7.3億t，從預測曲線圖和預測數據表中可知灰色組合模型預測結果是比較準確的，和規劃的預期目標大體一致，因此較可信。吞吐量預測值較高，因此青島港的港口承載力建設水平有待提高，未來港口的發展必定需要投入大量資金以服務于青島市整體經濟發展。

根據對青島市進出口貿易總額以及港口吞吐量這兩方面的預測結論可以發現：未來青島市港口物流服務需求量較大，增長態勢明顯，青島市港口運輸需求有充足的市場保證，運輸能力有一定的發展空間。青島港有堅實的腹地經濟予以支持，借助“一帶一路”，并能得到各種有利政策的支持，導致現在的承載能力與未來的需求量之間存在著一定的缺口，當前對港口物流的投資建設與實際經貿增長并不相符。因此，應加強基礎設施的投入建設，適當擴大其吞吐能力，保證港口運輸服務供給總量平衡，促進經貿又好又快發展。

4 結論

青島港吞吐量2017年位列全國第七，增速為1.6%，采用合理的數學模型對其未來吞吐量進行預測對港口發展具有重要價值。本文采用時間序列模型和灰色預測模型分別對青島港的運輸需求量以及港口承載力進行預測分析，取得了較好的效果。青島港應積極配合國家“一帶一路”倡議，依據所預測的港口吞吐量以及自身特色找到適合自己的發展策略，努力建設區域性國際航運中心和區域性國際物流中心的核心載體。