電動助力轉向系統的智能控制研究

彭 滔，周 鵬，胡桃川

(重慶理工大學 兩江人工智能學院， 重慶 401135)

隨著對汽車行駛安全要求的不斷提高，人們對汽車的平順性和操縱穩定性也提出了越來越高的要求。通過合理設計車輪定位參數可以使得汽車具有一定的回正能力，從而提高汽車的操縱穩定性，但卻增加了汽車轉向阻力。特別是在低速行駛時，容易造成駕駛員疲勞，不利于駕駛時舒適性的提高。汽車助力轉向系統通過借助外力來提高轉向能力，對提高汽車操縱穩定性有十分積極的意義[1-2]。

汽車電動助力轉向(electric power steering,EPS)具有減輕自重、可移植性好、結構簡單、布置靈活等特點，緊扣未來汽車“綠色”、“智能”的發展主題，已成為當今汽車助力系統廣泛采用的主流技術，也是世界汽車技術發展的研究熱點之一[3-4]。

EPS是一套復雜的機電一體化系統，主要包括控制器、轉向盤轉矩傳感器、車速傳感器、電流傳感器、助力電機以及減速機構、機械式轉向器、電源等部分[5]。EPS控制的關鍵問題是根據汽車的運行狀態確定助力電機輸出力矩，并設計電機控制器實現助力電機力矩的跟蹤。

許多研究者從不同方面運用不同的方法進行了研究。任夏楠等[6]利用助力誤差，在高低兩種行駛工況下闡述了對阻力特性曲線的設計原理，并探討了EPS助力特性曲線的相關幾何特征。張永輝等[7]以駕駛員理想轉向盤力矩為依據，設計了電動汽車的助力特性曲線，對電動汽車EPS助力曲線進行了設計與評價。李志鵬等[4]針對采用PID控制的電動助力轉向系統中出現的積分飽和現象，提出了基于模糊和anti-windup變結構自適應PID的抗飽和特性控制器。李靖等[8]針對汽車EPS系統的非線性實時變化問題，通過模糊算法，設計了EPS的助力特性曲線，建立了助力電機電流和轉向桿位移的預測控制模型，實現對EPS的預測控制。孔令強等[9]通過建立包括機械模型、電動機模型、2自由度轉向模型和輪胎模型的EPS模型，設計了H∞輸出反饋控制器。趙萬忠等[10]利用EPS及整車的2自由度模型，通過構建系統狀態空間方程和增廣被控對象矩陣，運用H∞方法極小化系統中各種干擾對被控輸出的影響，并在此基礎上應用H2方法對系統進行優化。閆啟迪等[11]針對電動叉車電動助力轉向系統，基于2自由度模型設計了魯棒H∞控制器，并運用遺傳算法對控制器的加權函數參數進行優化。鄒左明[12]將系統的外界干擾、系統建模誤差等因素看作是一個廣義的外干擾系統，對系統可觀測干擾進行觀測，提出一種基于干擾觀測器的動態面滑模控制。王金波等[13]考慮駕駛員熟練程度，提出了一種跟蹤期望駕駛特性的汽車電動助力轉向系統控制策略，改善了汽車的操縱穩定性。陳國平等[14]在動力學模型的基礎上，考慮了系統存在的不確定因素，融合模糊邏輯和滑模變結構控制，研究了電動輪汽車差動轉向穩定性控制策略。

目前EPS系統常用的控制策略主要是PID，對系統中存在的模型不確定性和路面干擾等信息難以很好地控制。針對該問題，本文根據轉向盤轉矩信號和車速信號確定助力電機的目標轉矩，利用徑向基函數(radial basis function,RBF) 神經網絡對助力電機的電流參數設計智能控制器，通過助力電機快速跟蹤目標電流來實現助力電機施加在轉向軸上的助力轉矩快速跟隨目標轉矩，從而達到EPS轉向助力的目標。RBF神經網絡具有較好的自適應性和泛化性等優點，能彌補控制系統中的非線性、不確定性和未知信息等不利因素，提高了轉向控制系統的控制精度、魯棒性和自適應能力。

1 EPS動力學模型

EPS系統主要由控制器、傳感器、助力電機和機械結構等部件構成。對其進行動力學建模后得到方向盤、輸入轉向柱、助力電機、輸出轉向柱、齒輪齒條和左右輪等6個動力學元器件之間的動力學關系，系統結構如圖1所示[4]。

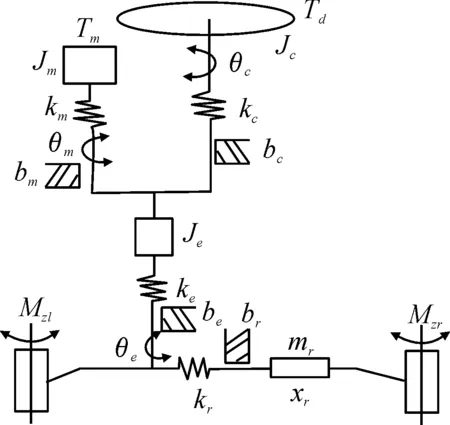
圖1 EPS系統結構

方向盤轉角和下轉向軸之間的動力學關系[4]為

(1)

其中：θc為方向盤的輸入轉角；θe為下轉向柱的轉角；Jc為方向盤轉動慣量；bc為方向盤阻尼系數；Td為方向盤輸入力矩；Kc為輸入轉向柱扭轉剛度。

助力電機與下轉向軸之間的動力學關系為

(2)

其中：θm為助力電機的轉角；Jm為助力電機轉動慣量；bm為助力電機阻尼系數；Tm為電機轉矩；Km為助力電機轉矩扭轉剛度；G為電機減速機構傳動比。

下轉向軸與齒輪齒條轉向器之間的動力學關系為

GKc(θm-Gθe)

(3)

其中：Je為下轉向柱轉動慣量；be為下轉向柱的阻尼系數；Kc為上轉向柱扭轉剛度；Ke為下轉向柱扭轉剛度；θe為下轉向柱的轉角。

齒轉齒條轉向器與其端作用力的動力學關系為

(4)

其中：xr為齒輪位移；mr為齒輪質量；br為齒輪阻尼系數；Kr為齒輪剛度；Fσ為齒輪端作用力；rp為小齒輪的分度圓半徑。

轉向器端作用力與車輪轉向角之間的動力學關系為

(5)

其中：JFω為車輪繞主銷的轉動慣量；bFω為繞主銷阻尼系數；KFωz為繞主銷轉動剛度；A為轉向器端到前輪的力臂傳動比；Mz為前輪的回正力矩；θFω為前輪轉角。

車輪回正力矩的動力學關系為

(6)

其中：Mzl為左前輪的回正力矩；Mzr為右前輪的回正力矩；γ為主銷后傾角；β為主銷內傾角。

2 智能控制器設計

2.1 控制策略

EPS控制方案包括上層的助力電機目標電流確定策略和下層的電流閉環控制策略兩個部分[15]。

助力電機目標電流的具體確定方法主要有實時計算法和利用助力特性曲線計算兩種方法。常用的方法根據轉向盤轉矩信號Td和車速信號V，利用助力特性曲線確定目標電流Im。助力電機利用反饋實測電流I與目標電流Im構成閉環，得到電流閉環控制結構示意圖，如2所示。

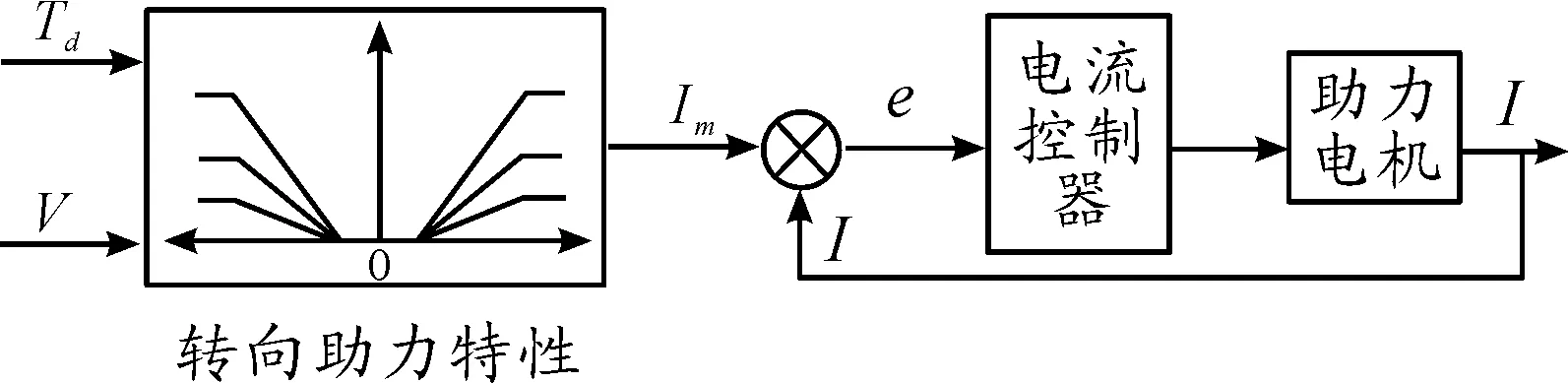
圖2 控制系統結構示意圖

常用的助力特性曲線有直線型、折線性和曲線型3類。本文中選用如圖3所示的直線型助力特性曲線來計算助力目標電流Im，其中Td為轉向盤轉矩。如圖3所示，在助力區內力矩Td與電流Im成線性關系，在某一車速范圍內的助力曲線函數可表達為[16]

(7)

其中：Td0為開始助力時轉向盤的輸入扭矩；Imax為助力電機最大工作電流；K(V)為助力增益系數。為了使駕駛員獲得更好的操作性和路感，助力特性曲線應能充分協調低速輕便、高速沉穩的助力特性，因此式(7)中的K(V)值隨車速的增加而減小。

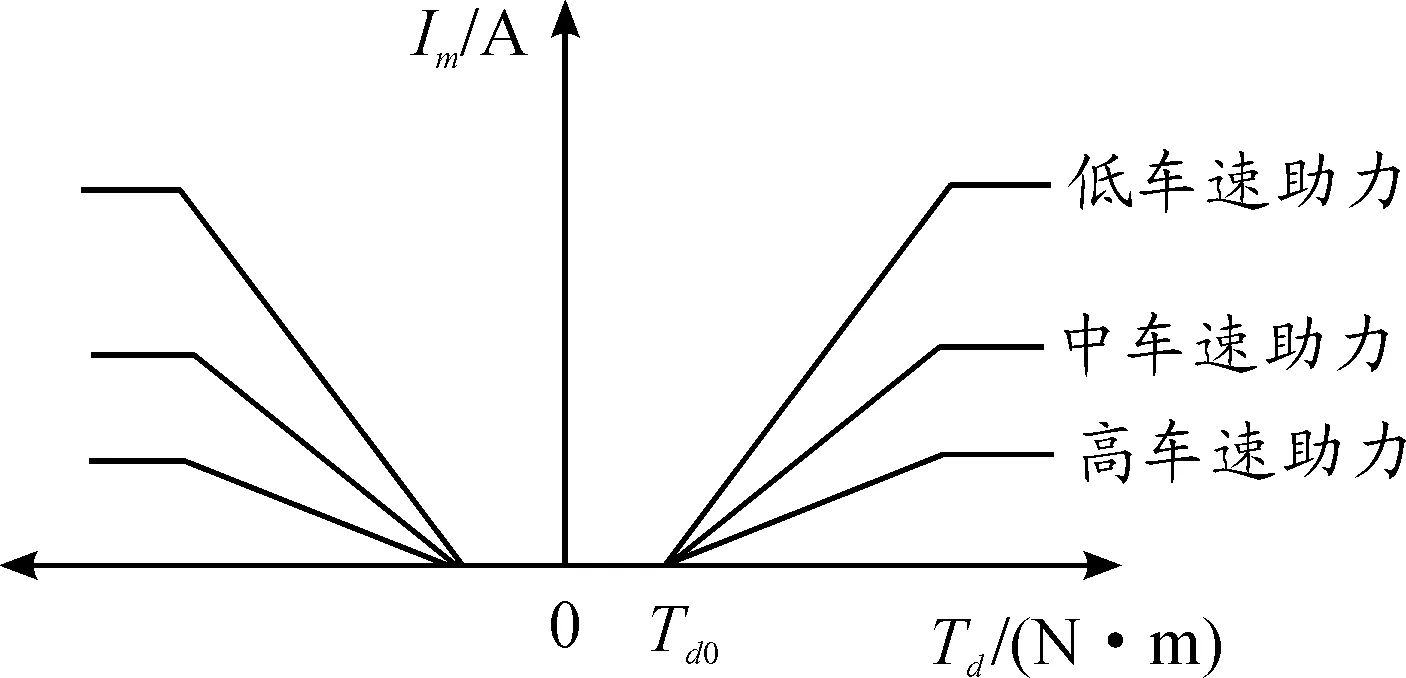
圖3 直線型助力特性曲線

2.2 智能控制器設計

電動助力轉向系統需要滿足穩定性、迅速性和準確性的要求，但電機中存在的強非線性和不確定性是控制器設計中的難點。神經網絡能以任意精度逼近任意非線性函數，具有自組織、自適應、自學習、泛化性和容錯性強等優點，能彌補控制系統中的非線性、不確定性和未知信息等因素的影響，提高魯棒性和自適應能力[17]。本文利用RBF神經網絡對任意非線性函數全局任意精度的逼近能力設計智能控制器，實現對系統的控制[18-21]。

2.2.1助力電機轉矩模型

本文采用永磁直流電機作為助力電機，由于電機自感電動勢很小，可以忽略不計。因此，電機端電壓Um與電樞的電阻R和電流Im、反電動勢常數Kb、轉速Nm之間的關系可以表示為[19]

Um=R·Im+Kb·Nm

(8)

由于轉矩與電樞電流成正比，可令Ka為轉矩常數，則式(8)可改寫為

Um=Ka·Tm+Kb·Nm

(9)

2.2.2神經網絡控制器設計

根據式(8)和(9)可知，電機轉矩有電壓和電流兩種控制方式，其中電壓控制是開環控制方式，而電流控制是通過電流傳感器測得電樞電流信號構成反饋通道形成的閉環控制方式。開環控制結構簡單，但控制精度不高，閉環控制則控制精度高，抗干擾能力強。

本文采用控制電流的閉環控制方式，利用RBF神經網絡對電流參數設計智能控制器，控制器中的神經網絡輸入為電流偏差信號(即狀態誤差)，輸出為電流的控制量，實現對電機轉矩控制。RBF神經網絡屬于一類線性化參數的神經網絡，可以表示為[20]

(10)

其中：Z=[z1,…,zq]∈ΩZ?Rq是輸入向量；W=[w1,…,wn]T∈Rn是權值向量；n>1是RBF神經網絡節點數；S(Z)=[s1(Z),…,sn(Z)]T；si(·)是徑向基函數，本文采用如下高斯函數定義：

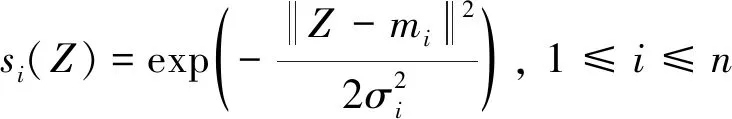
(11)

在助力轉向電機控制中，只有電流誤差信號Ie=I-Im這1個狀態輸入(即Z=Ie)，因此RBF神經網絡的輸入層只需要1個神經元，神經網絡輸出為

(12)

其中I是助力電機實際輸出電流。

2.2.3神經網絡學習算法

(13)

(14)

(15)

(16)

同理可得：

(17)

wi(n+1)-wi(n)=-η(I-Im)si(Z)

(18)

其中η為學習率。由式(16)～(18)可以對mi、σi、wi進行調整。

3 仿真研究

為了驗證本文所提方法的正確性和有效性，在北京中通天立公司研發的TAT-6/TL型“電動助力轉向在環仿真實驗臺”EPS實驗臺架(圖4)中，采集了分別代表低速(V=23.11 km/h)、中速(V=73.14 km/h)和高速(V=152.4 km/h)的3組數據，利用Matlab平臺進行仿真研究。

圖4 TAT- 6/TL型EPS實驗臺架

仿真研究中，選取神經元數n=100，參數初值為m=0，w=0，σ=1，學習率η=0.8。TAT- 6/TL型EPS實驗臺架中的助力特性函數為：

(19)

在仿真中，根據式(10)～(12)和(16)～(18)建立高斯函數神經網絡和參數更新，利用PID控制得到的數據對神經網絡進行訓練，得到mi、σi、ωi的值。再讀取轉矩信號Td和車速信號V的實驗數據，根據式(19)計算出對應的目標電流值Im，利用神經網絡控制器式(12)，得到助力電機實際電流值I。

將本文提出的智能控制效果與TAT- 6/TL型EPS實驗臺架中采用PID控制(參數分別為P=1，I=0.1，D=0)時的效果進行了對比，結果如圖5～10所示。

從圖5～7中可以看出：兩種控制方法的控制效果均是在低速時助力電流大，高速時助力電流小，符合助力轉向時保證駕駛員路感的要求。

從圖8～10中的控制電流誤差可以看出：本文提出的智能控制方法在3個速度的電流誤差整體明顯好于PID控制效果，在低速和高速階段的控制效果尤為明顯。在中速階段，雖然PID控制在[0,100]、[180,320]和[375,400]這3個時間段內表現出了良好的控制效果，控制誤差約為0，但在[100,180]和[320,375]兩個時間段內，誤差出現了較大波動，最大誤差達到-2.02，而智能控制的電流誤差幾乎在整個時間段內都保持在[-0.5,0.5]的范圍內。

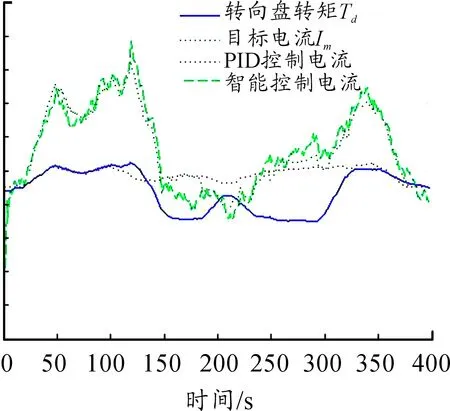
圖5 低速助力曲線(V=23.11 km/h)

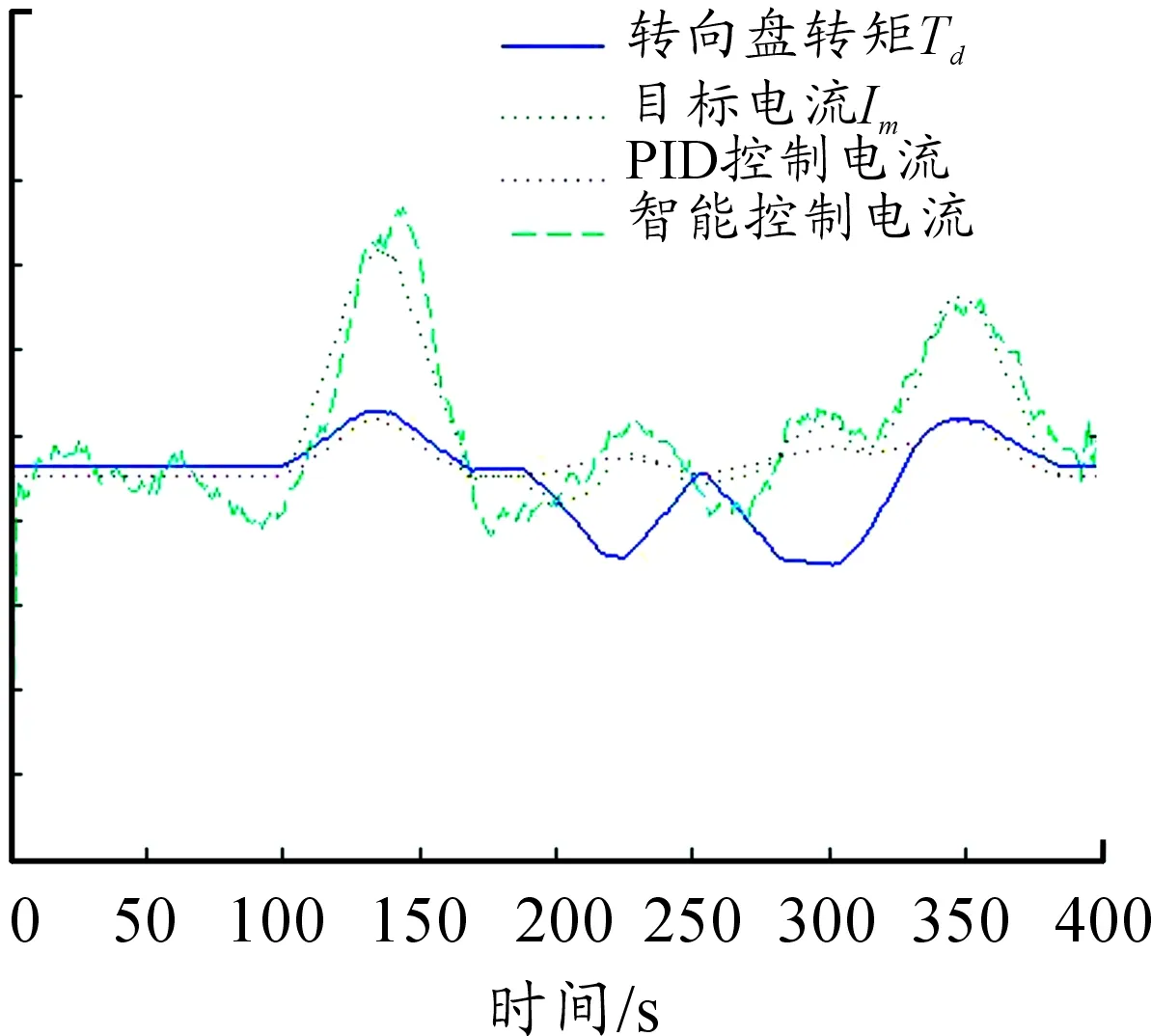
圖6 中速助力曲線(V=73.14 km/h)

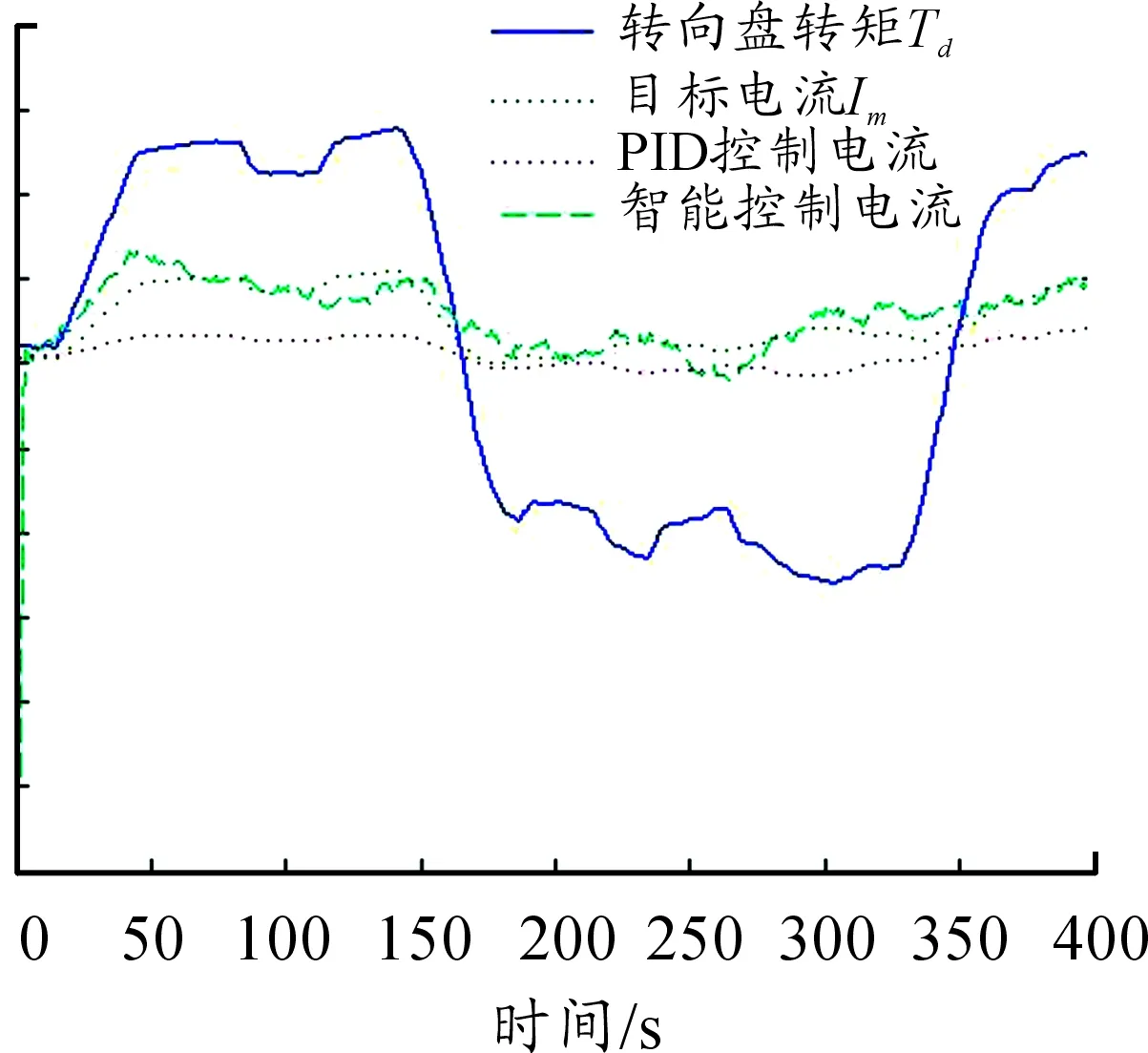
圖7 高速助力曲線(V=152.4 km/h)

圖8 低速助力電流誤差曲線

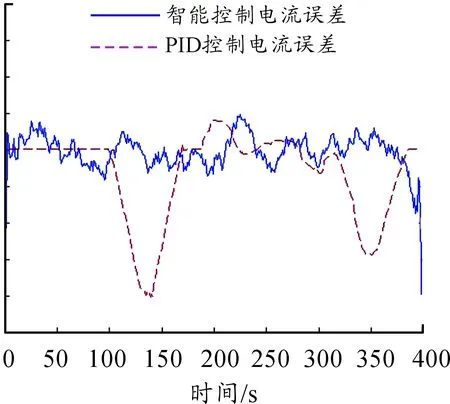
圖9 中速助力電流誤差曲線

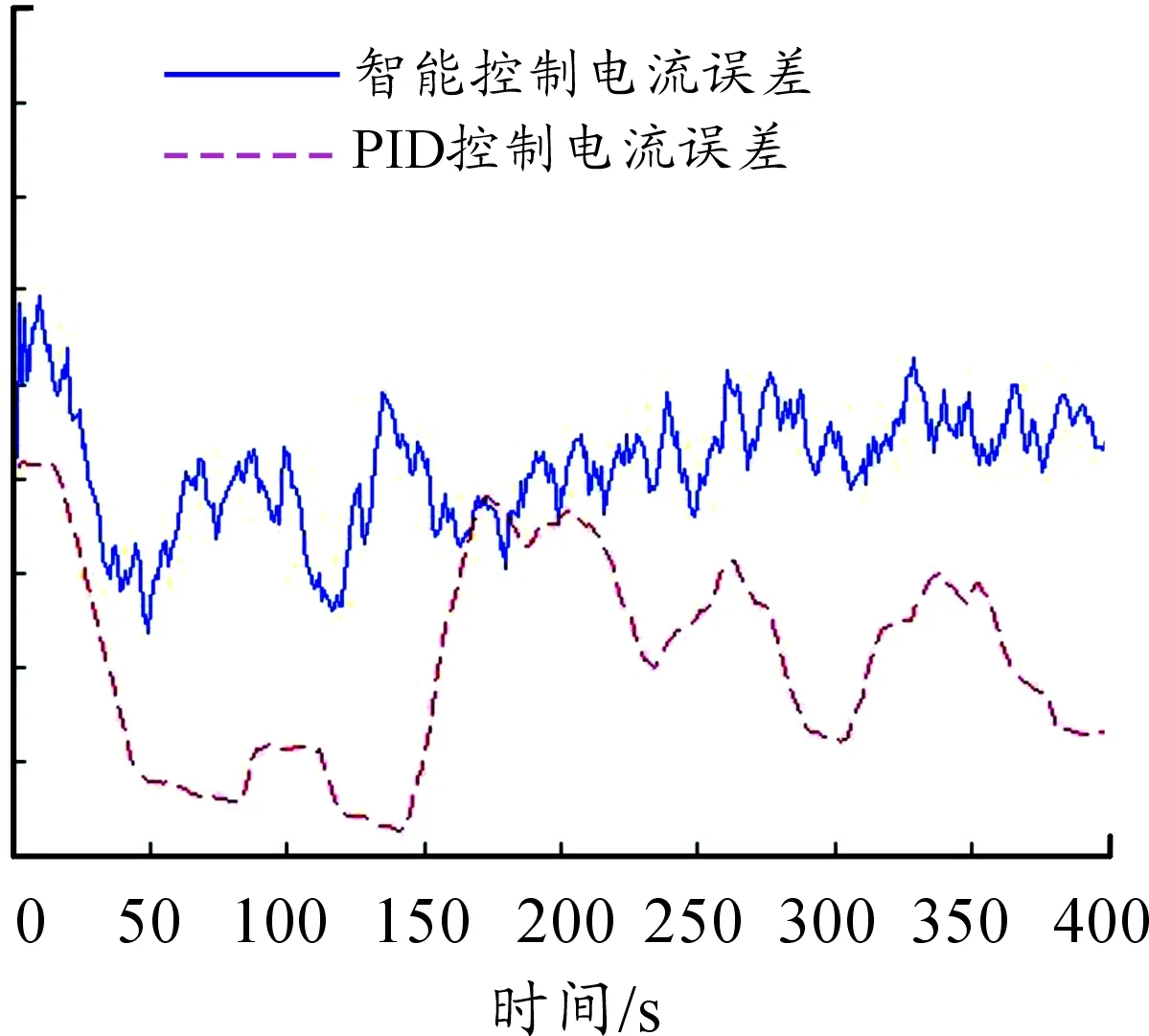
圖10 高速助力電流誤差曲線

通過對比分析認為：由于RBF神經網絡能彌補控制系統中的非線性、不確定性和未知信息等因素，使得本文提出的智能控制器有更好的控制精度和平穩性，提高了電動助力轉向系統的魯棒性和自適應能力。

4 結束語

本文基于EPS提出了一種智能控制方法，利用直線型助力特性曲線確定目標電流，再利用RBF神經網絡對助力電機電流設計了控制器，并利用BP學習算法對神經網絡權值、中心點和方差進行調節。該方案易于實現，同時保證了轉向控制系統具有較高自適應性和控制精度，并通過采集實驗臺架不同速度下的實驗數據進行仿真研究，驗證了所提控制方案能實現EPS的助力控制。