小策略 大智慧

李兆龍

“四邊形”這部分的知識點包括平行四邊行、矩形、菱形、正方形以及三角形中位線等，它們既自成體系，又相互聯系。下面以部分中考真題為切入點，以幫助同學們獲取解題技巧，舉一反三。

考點一 多邊形的概念與性質

例1 （2018·北京）若正多邊形的一個外角是60°，則該正多邊形的內角和為（ ）。

A.360° B.540° C.720° D.900°

【解析】根據“多邊形的邊數與多邊形的外角的個數相等”，可求出該正多邊形的邊數，再由多邊形的內角和公式求出其內角和。該正多邊形的邊數為：360°÷60°=6，該正多邊形的內角和為：（6-2）×180°=720°。故選：C。

例2 （2018·山東濟寧）如圖1，在五邊形ABCDE中，∠A+∠B+∠E=300°，DP、CP分別平分∠EDC、∠BCD，則∠P=（ ）。

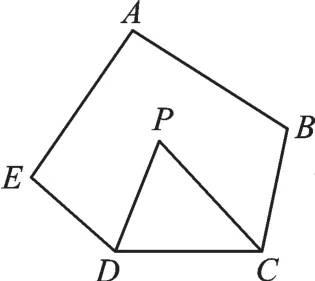
圖1

A.50° B.55° C.60° D.65°

【解析】先根據五邊形內角和求得∠EDC+∠BCD，再根據角平分線性質求得∠PDC+∠PCD，最后根據三角形內角和求得∠P的度數。

解：∵在五邊形ABCDE中，∠A+∠B+∠E=300°，

∴∠EDC+∠BCD=240°，

又∵DP、CP分別平分∠EDC、∠BCD，

∴∠PDC+∠PCD=120°，

∴在△CDP中，∠P=180°-（∠PDC+∠PCD）=180°-120°=60°。

故選：C。

考點二 一般平行四邊形性質及判定

例3 （2018·廣西玉林）在四邊形ABCD中：①AB∥CD；②AD∥BC；③AB=CD；④AD=BC，從以上條件中選擇兩個條件使四邊形ABCD為平行四邊形的選法共有（ ）。

A.3種 B.4種 C.5種 D.6種

【解析】根據平行四邊形的判定方法，①②、③④、①③、②④均可判定四邊形ABCD是平行四邊形。故選：B。

例4 （2018·湖北孝感）如圖2，B、E、C、F在一條直線上，已知AB∥DE，AC∥DF，BE=CF，連接AD。求證：四邊形ABED是平行四邊形。

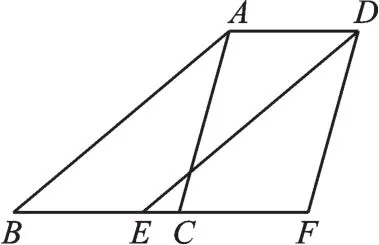
圖2

【解析】已知AB∥DE、AC∥DF，利用平行線的性質可得出∠B=∠DEF、∠ACB=∠F，由BE=CF可得出BC=EF，進而可證出△ABC≌△DEF，根據全等三角形的性質可得出AB=DE，再結合AB∥DE，即可證出四邊形ABED是平行四邊形。

證明：∵AB∥DE，AC∥DF，

∴∠B=∠DEF，∠ACB=∠F。

∵BE=CF，

∴BE+CE=CF+CE，

∴BC=EF。

∵ ∠B=∠DEF，∠ACB=∠F，BC=EF，

∴△ABC≌△DEF（ASA），

∴AB=DE。

又∵AB∥DE，

∴四邊形ABED是平行四邊形。

考點三 特殊平行四邊形性質及判定

例5 （2018·四川眉山）如圖3，在?ABCD中，CD=2AD，BE⊥AD于點E，F為DC的中點，連接EF、BF，下列結論：①∠ABC=2∠ABF；②EF=BF；③S四邊形DEBC=2S△EFB；④∠CFE=3∠DEF，其中正確結論的個數共有（ ）。

圖3

A.1個 B.2個 C.3個 D.4個

【解析】如圖4，延長EF交BC的延長線于G，取AB的中點H，連接FH。想辦法證明EF=FG、BE⊥BG、四邊形BCFH是菱形即可解決問題。

解：如圖4，延長EF交BC的延長線于G，取AB的中點H，連接FH。

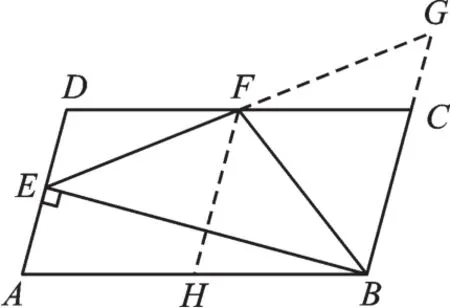
圖4

∵CD=2AD，DF=FC，

∴CF=CB，

∴∠CFB=∠CBF，

∵CD∥AB，

∴∠CFB=∠FBH，

∴∠CBF=∠FBH，

∴∠ABC=2∠ABF。故①正確。

∵DE∥CG，

∴∠D=∠FCG，

∵DF=FC，∠DFE=∠CFG，

∴△DFE≌△CFG，

∴FE=FG，

∵BE⊥AD，

∴∠AEB=90°，

∵AD∥BC，

∴∠AEB=∠EBG=90°，

∴BF=EF=FG。故②正確。

∵S△DFE=S△CFG，

∴S四邊形DEBC=S△EBG=2S△BEF。故③正確。

∵AH=HB，DF=CF，AB=CD，

∴CF=BH，

∵CF∥BH，

∴四邊形BCFH是平行四邊形，

∵CF=BC，

∴四邊形BCFH是菱形，

∴∠BFC=∠BFH，

∵FH∥AD，BE⊥AD，

∴FH⊥BE，

∵FE=FB，

∴∠BFH=∠EFH=∠DEF，

∴∠EFC=3∠DEF。故④正確。

故選：D。

例6 （2018·山東青島）已知：如圖5，平行四邊形ABCD，對角線AC與BD相交于點E，點G為AD的中點，連接CG，CG的延長線交BA的延長線于點F，連接FD。

（1）求證：AB=AF。

（2）若AG=AB，∠BCD=120°，判斷四邊形ACDF的形狀，并證明你的結論。

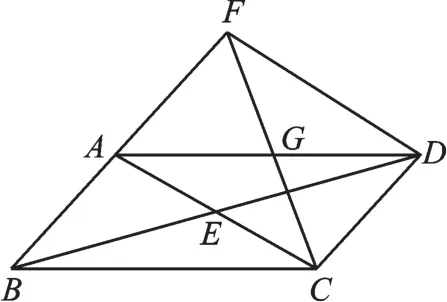
圖5

【解析】（1）只要證明AB=CD、AF=CD，即可解決問題；（2）結論：四邊形ACDF是矩形。根據“對角線相等的平行四邊形是矩形”判斷即可。

證明：（1）∵四邊形ABCD是平行四邊形，

∴AB∥CD，AB=CD，∴∠AFC=∠DCG，

∵GA=GD，∠AGF=∠CGD，

∴△AGF≌△DGC（ASA），

∴AF=CD，

∴AB=AF。

解：（2）四邊形ACDF是矩形。

理由：∵AF=CD，AF∥CD，

∴四邊形ACDF是平行四邊形，

∵四邊形ABCD是平行四邊形，

∴∠BAD=∠BCD=120°，∴∠FAG=60°，

∵AB=AG=AF，

∴△AFG是等邊三角形，

∴AG=GF，

∵△AGF≌△DGC，

∴FG=CG，

∵AG=GD，

∴AD=CF，

∴四邊形ACDF是矩形。

考點四 三角形的中位線

例7 （2018·遼寧大連）如圖6，在Rt△ABC中，∠ACB=90°，D、E分別是AB、AC的中點，連接CD，過E作EF∥DC，交BC的延長線于F。

（1）證明：四邊形CDEF是平行四邊形。（2）若四邊形CDEF的周長是25cm，AC的長為5cm，求線段AB的長度。

圖6

【解析】（1）由三角形中位線定理可推知ED∥FC，2DE=BC，然后結合已知條件“EF∥DC”，利用兩組對邊相互平行，得到四邊形CDEF為平行四邊形。

（2）根據“在直角三角形中，斜邊上的中線等于斜邊的一半”，得到AB=2DC，即可得出四邊形DCFE的周長=AB+BC，故BC=25-AB，然后根據勾股定理即可求解。

證明：（1）∵D、E分別是AB、AC的中點，F是BC延長線上的一點，

∴ED是Rt△ABC的中位線，∴ED∥FC。∵EF∥DC，

∴四邊形CDEF是平行四邊形。

解：（2）∵四邊形CDEF是平行四邊形，∴DC=EF，

∵DC是Rt△ABC斜邊AB上的中線，∴AB=2DC，

又∵BC=2DE，DE=CF，

∴四邊形DCFE的周長=AB+BC=25，

∴BC=25-AB，

∵在 Rt△ABC 中，AB2=BC2+AC2，即 AB2=（25-AB）2+52，

解得，AB=13cm。

“四邊形”是中考重點考查的內容，題型靈活多變，不僅可以直接應用四邊形的有關性質和判定，而且還能應用三角形的有關知識解決問題。