結合膜計算與人工蜂群算法的K均值算法

黃文成

（西華大學計算機與軟件工程學院，成都 610039）

0 引言

聚類是一種重要的無監督學習技術，其目標是將數據集合分成若干簇，使得同一簇內的樣本相似度盡可能大，而不同簇間的樣本相似度盡可能小，目前該技術在機器學習、模式識別、Web挖掘以及圖像量化等領域得到了廣泛的應用[14]。

K均值（K-means）算法是解決聚類問題的經典算法之一。但由于K均值聚類算法敏感于初始值和易受孤立點影響,容易陷入局部最優,并且全局搜索能力較弱,這些致命點嚴重影響聚類的性能[16]。為解決函數優化問題，由Karaboga于2005年提出了人工蜂群算法（Artificial Bee Colony Algorithm，ABC）[12,13]，該算法是一種模擬生物群體智能的優化方法，具有實現簡單、參數數量較少、全局搜索能力好、魯棒性強等多種優點。但ABC算法還是存在收斂速度較慢、較容易陷入局部最優等問題。

近年，研究人員考慮到兩種算法有許多互補之處，著手研究將兩種算法進行結合。李海洋等人[17]提出IABC-K算法，將ABC算法和K-means算法進行合理切換，應用于圖像分割。曹永春等人[18]提出IABCC算法，使用ABC算法和K-means算法對數據進行交替迭代。喻金平等人[3]提出IABC-Kmeans算法，使用ABC算法和K-means算法在對數據進行交替迭代的同時，并對適應度函數及初始值的獲取進行了改良。Janani等人[19]提出ABC-BK算法及新的適應度函數，并將此算法應用于文本聚類。Alam等人[20]提出WDC-KABC算法應用于網頁文獻聚類。Cong等人[21]提出EABCK算法，將K-means算法應用于由ABC算法得到的全局最優值的再次尋優。Giuliano等人[22]提出ABCk算法，將K-means算法嵌入到ABC算法的雇傭蜂和觀察蜂階段，加快算法收斂速度。Bonab等人[23]提出CCIAABC-K算法，應用于對數據的聚類和圖像的分割。這些混合算法大多克服了K-means算法對初始值敏感，ABC算法收斂速度慢的問題。但是，初始值的選取還是對混合算法的結果有影響，也存在著容易陷入局部最優,求解精度和算法不太穩定的問題。

鑒于以上的問題，本文將膜計算（Membrane Computing，MC）[24]的概念組合到 K-means和ABC的混合算法中，提出一種結合膜計算與人工蜂群算法的K均值算法（K-means algorithm:Combining P system with Artificial Bee Colony Algorithm，PABC-K）來優化聚類問題。

1 準備知識

1. 1 K均值算法

K均值算法因其簡單性和易于實現而被廣泛使用。K均值算法根據參數K將給定數據集聚類為K個簇，以每個數據點到其聚類中心的距離平方和為目標函數,通過求解函數極小值方式反復迭代,直到目標函數收斂。

K均值聚類目標函數為：

K均值聚類中心迭代公式為：

其中，N為數據樣本數；K為聚類中心數；Xj為第j個數據點；Ci為第i個聚類中心；wji為權重，當第j個數據點屬于第i個聚類中心時，其值為1，如不屬于，則為0。

1. 2 ABC算法

ABC算法通過模擬蜂群分工合作尋找最優蜜源的過程求解優化問題，是一種基于蜜蜂群體智能的優化算法[1]。ABC算法具有控制參數少、易于實現等優點，在函數優化方面具有比較好的表現。在ABC算法中，蜜蜂被分為雇傭蜂、觀察蜂和偵查蜂這3類。食物源的位置表示一個可行解，每個食物源只對應一只雇傭蜂，即雇傭蜂的數量等于食物源的數量。觀察蜂的數量則設置為和雇傭蜂相同。ABC算法的基本步驟如下：

步驟1：種群的初始化。設具有n個樣本點的數據集X={xi∈Rd,i=1,2,…,n},xi為d維向量；設算法的最大迭代次數為MCN，每個蜜源的最大開采次數為limit，蜜源個數為SN。

步驟2：根據如下公式（3）隨機選擇蜜源，作為初始可行解：

其中，j∈{1,2,…,d}；Xij表示第 i個蜜源的第 j維分量；Lj表示所有樣本中第j維的數值下限；Uj表示所有樣本中第j維的數值上限。

步驟3：雇傭蜂根據公式（4）在當前蜜源的鄰域范圍內更新蜜源。運用貪婪選擇法，比較新舊解的適應度，保留質量好的解：

其中，i,k∈{1,2,…,SN}，且i≠k。

步驟4：每個雇傭蜂更新蜜源后，觀察蜂選擇一只雇傭蜂，跟隨其前往蜜源采蜜。觀察蜂選擇雇傭蜂的概率計算公式如式（5）所示：

其中，fi為第i個蜜源的適應度值。觀察蜂通過公式（5）選著比較好的蜜源，隨后根據公式（4）再次更新蜜源。

步驟5：某蜜源的搜索次數達到最大開采次數Limit,但蜜源適應度不再變化時,放棄該蜜源。同時,將雇傭蜂轉換為偵察蜂。偵察蜂根據公式（3）搜尋新的蜜源，以代替被放棄的蜜源。

步驟6：判斷是否達到最大迭代次數達或滿足循環終止條件。若是,算法結束并輸出適應度最好的蜜源作為最優解。若不是,返回步驟3。

1. 3 膜計算

膜計算又稱為P系統，是羅馬尼亞科學院院士Gheorghe Paun于1998年11月基于細胞膜結構提出的一種自然計算方法[2]。Nishida[4]在2004年將膜計算引入到遺傳算法中，第一次提出了膜優化算法的概念。膜計算還被引入到了粒子群算法[5]、人工魚群算法[6]及K-medoids[7]、KNN[8]等算法中。膜優化算法已成為了膜計算領域中的一個重要分支。同時，P系統也被大量應用于圖像分割方向[9-11],并且獲得了比較好的結果。

P系統具有分布式、極大并行性和非確定性的特點。根據膜結構的特點，P系統可以分為細胞型P系統、組織型P系統和神經型P系統。其中細胞型P系統是其他兩種P系統的基礎[2]。細胞型P系統的基本結構如圖1所示。最外層的細胞膜（1號膜）稱為表層膜，它分隔開外部環境和內部空間；膜內部沒有其他膜存在的細胞膜，被稱為基本膜（2、4、5號膜）。在P系統中，各個膜的空間中可以具有各自不同的對象和運算規則。

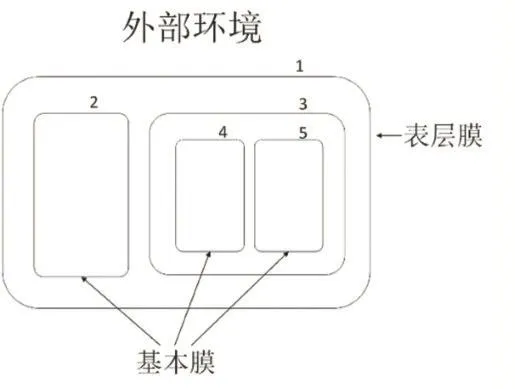
圖1 細胞型P系統的結構

形式上，一個細胞型P系統定義如下：

其中：O是對象的有限字母表；Σ?O是輸入字母表；μ是由q個膜組成的膜結構，q稱為P系統Π的度數；Mi（1≤i≤q）表示q個膜中各自包含的對象；Ri（1≤i≤q）表示q個膜中各自包含的規則；i0∈{0,1,2,…,q}是系統Π的輸出膜。

規則Ri是二元組（u,v），通常寫成u→v,u是字母表O中的字符串,v是O×{here,out,in}上的一個字符串。其 中，v具 有（a,tar）的 形 式，其中a∈O,tar∈{here,out,in}。如果tar=here，則a位于規則所在的區域中；如果tar=out，則a被傳送到規則所在的區域的高一級區域中；如果tar=in，則a被傳送到規則所在的區域的低一級區域中。

2 PABC-K算法

2. 1 最大最小距離積法初始化

無論K均值算法還是人工蜂群算法都對初始值敏感,而隨機的初始化影響著算法的收斂速度和最優解的質量。文獻[3]針對最大最小距離法和最大距離積法的不足，提出最大最小距離積法來對初始值進行初始化，以解決初始點過于密集等問題。

算法流程圖如圖2所示。其中，D是包含所有數據的集合；k是要選取的初始點個數；Z是存儲k個初始點的集合，算法開始前為空集；Temp是存儲Z中各元素到D中各元素的距離的數組。

該算法所需參數少；可以選取到點密度較大的點，稀疏了初始點的分布；通過乘積法放大了點與點之間的差異，選取過程更具區分度。

2. 2 膜系統結構

PABC-K算法建立在細胞型P系統的基礎上，采用單層膜結構，如圖3所示。0號膜為表層膜，分隔開外部環境和內部空間。表層膜內部具有n個細胞膜，全部都為基本膜。基本膜之間可以相互交流，基本膜和表層膜也可以相互交流。

圖2 最大最小距離積算法流程圖

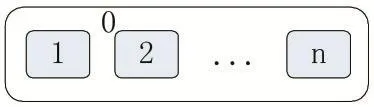
圖3 單層膜結構

PABC-K算法中，多種群蜂群與P系統結合，每個基本膜中存在一個蜂群，表層膜中不包含蜂群。在每次的迭代過程中，每個基本膜中的信息通過表層膜進行交互，每個基本膜中的蜂群相互間不產生影響。表層空間能夠獲取各基本膜滲透出來的局部最優食物源，通過貪婪選擇法，選出全局最優食物源。表層膜空間將全局最優食物源，分別滲透回每個基本膜中，用以影響各基本膜中下一次進行的迭代。

該P系統的定義如下：

（1）Π =(O,μ,(M0,...,Mn),R,i0)

（2）O是整個樣本集

（3）膜結構包含n個細胞膜，具體結構μ=[[]1,[]2,[]3,...,[]n]0，其中0表示表層膜。

（4）初始種群的分布為：

M0=φ1=O,M2=O,…,Mn=O

其中，M0為皮膚膜的初始集，是一個空集。Mi（1≤i≤n）為每個基本膜，包含對象都為整個樣本集。

（5）輸出字母表io表示表層膜的輸出，也是PABC-K算法的最終輸出，表示一組食物源。

細胞膜空間中的規則：

（1）每個基本膜中都獨立運行K-means算法與ABC算法的混合算法；表層膜空間內進行貪婪選擇法的進化規則。

（2）各基本膜將各自運算出的最優的食物源發送至表層膜；表層膜則將最終得到的最優的個體復制n份發送回各基本膜。

2. 3 結合膜計算與人工蜂群算法的K均值算法

在PABC-K算法中，以膜系統作為總體框架，結合人工蜂群算法來優化K-means算法的聚類中心，用以對數據進行聚類運算。本算法設計了一個細胞型P系統，它是一個帶有進化規則和轉運規則的P系統，使用單層膜結構，具有一個表層膜和n個基本膜。每個基本膜中都有進化規則和多個對象，并且每個對象都與表層膜之間有轉運規則。由ABC算法和K-means算法相結合的混合算法作為每個基本膜中的進化算法，作用于將要進行聚類的數據。各基本膜與表層膜間運用轉運規則，將各基本膜中得到的局部最優解轉運到表層膜空間中，并接收表層膜空間得到的目前狀態的全局最優解，轉運回各基本膜空間中。表層膜中將使用貪婪選擇法作為進化規則，作用于從各基本膜得到的局部最優解，得到全局最優解，并運用轉運規則傳回各基本膜中。

每個基本膜中，都存在著一個蜂群，單獨運行由ABC算法和K-means算法相結合的混合算法，尋找最優食物源。食物源個數設置為k，每個食物源代表一個聚類中心點；設置最大迭代次數MCN。

在混合算法中，使用前文介紹的最大最小距離積法對食物源進行初始化，得到適應度較好的初始食物源。在雇傭蜂階段，使用K-means算法來加強局部尋優能力，同時加快對目標函數的收斂速度。由于K-means算法的快速收斂，對局部最優值能較準確的搜尋，在雇傭蜂階段就能將所有食物源的局部最優值尋出。在ABC算法中，觀察蜂主要作用于優質食物源，起到加快收斂的作用；而在本算法中，由于K-means算法的作用，在雇傭蜂階段就已將所有食物源的適應度函數收斂，替代了觀察蜂的作用，故在本算法中將雇傭蜂階段省去。通過表層膜得到的全局最優值將作用于偵查蜂階段，偵查蜂階段主要是將食物源更新，避免整體算法陷入局部最優值；將全局最優值加入到食物源的更新過程，加強了食物源更新的目的性，有利于整體算法收斂速度的加快。

PABC-K算法的總體流程圖如圖4所示。

圖4 PABC-K算法流程圖

3 實驗結果與分析

為了驗證本文中PABC-K算法進行聚類的有效性，從UCI數據集中選取4組真實數據集進行試驗。對每組數據集，分別用K-means算法、人工蜂群（ABC）算法、文獻[25]中提出的ABC算法的改進算法（Cooperative ABC,CABC算法）、文獻[22]中提出的融合了ABC算法和K-means算法的ABCk算法以及本文提出的結合膜計算與人工蜂群算法的K均值算法（PABC-K算法）進行算法聚類，并對結果進行比較分析。

4組測試數據集分別為UCI數據集中的Wine、Iris、CMC以及Glass數據集。

表1 各算法簇間距離的比較

對于每個數據集，每個算法單獨運行20次。表1顯示了通過20次實驗，各算法適應度的最優值，最差值，平均值以及標準差。適應度如1.1小節中公式（1）所示，數值越小，代表聚類效果越好。

由表1中數據可以看出：K-means算法的標準差較大，對初始值具有敏感性，容易陷入局部最優，穩定性偏差。ABC算法、ABCk算法、CABC算法都對數據集具有較好的聚類效果，與K-means算法相比具有較大的提高，穩定性提高也比較大。ABCk算法是ABC算法和K-means算法的結合算法，可以看出其聚類效果要略差于ABC算法和CABC算法，這是由于K-means算法對初始值敏感的缺點對該結合算法產生了影響，但是ABCk算法克服了ABC算法收斂緩慢的缺點。本文提出的PABC-K算法對聚類也取得了比較好的結果，在4個數據集上得到的標準差都十分低，該算法的穩定性十分好，能很好的擺脫對初始值的敏感；同時，由于K-means算法的加入，大大加快了本算法的收斂速度。

除了在Wine數據集上的聚類結果比其余4種算法的聚類效果稍差外，在Iris數據集、CMC數據集和Glass數據集上，都取得了很好的聚類效果。經過分析，Wine數據集中的樣本某一維的數據值遠遠大于其余維數上的數據值，在通過歐式距離進行聚類時，該維的數據對聚類的結果產生了嚴重的影響，掩蓋了其余維數上數值間的差別。雖然該算法對數據集具有比較好的聚類效果，但是正確分類的準確率卻不是太高。在Iris數據集上取得了約90%的準確率，但是在其余3個數據集上獲得的準確率并不高。這個也再次說明基于歐氏距離進行的聚類有一定的限制性，并不能適用于所有的數據集。

4 結語

本文根據ABC算法、K-means算法和膜計算這3種算法的優點和缺點，在膜計算的框架下，以ABC算法為基礎結合K-means算法，提出了PABC-K算法。以最大最小距離積法初始化蜜源，K-means算法嵌入到雇傭蜂階段加快算法收斂速度，膜計算作為整體框架涉及整個算法的各階段。算法通過在4個公開的標準數據集上運行，驗證了其具有較好的聚類效果和較高的穩定性。根據實驗中算法產生的結果以及相應的分析，進一步的研究將著重于對數據的預處理（如歸一化預處理等）和算法目標函數的改進。