小衛星對上面級定向的姿控設計與驗證

(北京宇航系統工程研究所，北京 100076)

0 引言

上面級能夠進一步將有效載荷從準地球軌道或地球軌道送入預定工作軌道或預定空間位置的具有自主獨立性的飛行器[2]。在軌服務中一項非常重要的關鍵技術便是服務航天器自主逼近與捕獲目標航天器的相對位置和姿態控制技術[1]。小衛星為上面級平臺載荷，小衛星姿態控制系統主要任務是，通過調姿使小衛星的固定面朝向上面級平臺方向，并克服展開機構展開時產生的干擾，使固定面穩定指向上面級平臺。小衛星的姿態控制系統需具備速率阻尼和對上面級平臺定向的功能。另外，由于小衛星在上面級平臺上的安裝已固定，當小衛星與上面級分離后，測控天線不朝地球方向，而且在對上面級定向后，測控天線無法朝向地球方向，這樣會導致地面測控站無法收到遙測數據。所以，小衛星姿控的難點在于如何實現快速對上面級平臺定向，并在對上面級平臺定向完成后如何實現測控天線是朝向地球的。本文針對小衛星的這些難點，開展小衛星定姿算法、姿控算法的設計，并通過數學仿真、半實物仿真以及飛行試驗對設計的姿控系統進行驗證。

1 姿控系統任務分析

小衛星與上面級分離時，小衛星在分離裝置內沿分離裝置內的滑軌滑行2s，之后小衛星與分離裝置分離，小衛星將以分離時刻的姿態角速度在空間中運動。小衛星的姿態控制系統需克服各種空間環境的干擾，使小衛星飛行器姿態穩定，并使小衛星的固定面朝向上面級平臺，為上面級平臺的光學跟瞄裝置提供遠距離跟瞄的條件。在試驗過程中需將遙測數據下傳，需小衛星的姿控進行調姿，使測控天線朝向地球，為建立遙測天地鏈路提供條件。

2 系統硬件設計

2.1 軟件設計思路和編程方法

針對小衛星任務需求，小衛星的姿態控制需完成星箭分離后的速率阻尼、對上面級平臺定向的功能，本系統采用連續型時變輸出執行機構(飛輪控制)，利用簡化的數學模型和輸出反饋控制可以設計具有一定魯棒性和優化性能的控制器以實現姿態控制[4]。小衛星分離后，首先進入無控模式，隨后進行速率阻尼模式，在三軸姿態角速度小于0.1°/s或時間到達一定時間后，由速率阻尼模式轉入對上面級平臺定向模式，展開帆板后一直保持對上面級平臺定向，直至任務結束。根據任務的功能要求，設計小衛星為零動量三軸穩定系統，使用1個三軸陀螺作為姿態敏感器、3個反作用飛輪沿小衛星本體正交安裝作為姿控系統的執行結構，采用4階龍格庫塔積分算法進行定姿，速率阻尼階段采用角速率反饋控制，對上面級平臺定向階段采用遞階飽和PD控制。

在姿控方案中使用飛輪對小衛星進行速率阻尼，通過陀螺積分定姿與遞階飽和PD控制算法，以實現小衛星對上面級平臺的快速定向；在對上面級平臺定向的過程中，通過繞小衛星本體x軸轉動一個角度(具體數值可根據分離時刻的軌道位置確定)，可實現測控天線超向地球。下面首先描述小衛星的姿態運動學與動力學，然后分別設計定姿算法與姿控算法。

2.2 姿態運動學與動力學模型

由于小衛星本體和展開機構均為剛性結構，所以，小衛星的姿態描述可用剛體的姿態模型描述，由于小衛星姿態存在大角度姿態機動，使用歐拉角描述姿態運動可能出現奇異問題，為了避免該問題，使用姿態四元數描述小衛星的姿態運動。

定義q為小衛星本體相對于慣性空間的姿態四元數，定義ω為小衛星相對慣性空間的姿態角速度，則小衛星的姿態運動學方程可描述為：

(1)

(2)

式中，q0為姿態四元數q的標部；qv為姿態四元數的矢部；ω×為ω的反對稱陣。

姿態四元數滿足歸一化約束，即：

q02+qvTqv= 1

(3)

將微小衛星視為剛體，動力學方程可表示為[3]：

(4)

式中，Is為小衛星的轉動慣量矩陣；h為小衛星的角動量；Tc和Td分別為作用在小衛星上的控制力矩和干擾力矩。

2.3 定姿算法設計

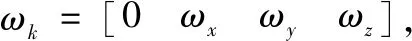
(5)

(1)計算k1：

k1=qk-1?ωk-1

(6)

式中，?表示四元數乘法。

(2)計算k2：

(7)

(3)計算k3：

(8)

(4)計算k4：

(9)

綜上，可確定當前時刻的姿態四元數為：

(10)

2.4 姿控算法設計

由于小衛星與上面級平臺分離后會具有一定的姿態角速度，因此，要實現小衛星對上面級平臺的快速定向，首先需要將小衛星的姿態角速度快速降低，為小衛星對上面級平臺定向做好準備，可通過速率阻尼的方式實現這一目標。速率阻尼完成后，需要調整小衛星的三軸姿態，將小衛星固定面快速調至對上面級平臺的方向，即通過對上面級平臺定向的模式來實現這一目標。

2.4.1 角速度反饋控制

采用角速度反饋控制的方式，可實現小衛星姿態角速度的快速阻尼，將小衛星的姿態角速度阻尼至較小值后，再轉入對上面級平臺定向模式。

角速度反饋控制律如下：

Tc=-kdampω

(11)

其中： 阻尼系數kdamp為三維正定對角陣。

2.4.2 遞階飽和PD控制算法設計

遞階飽和PD控制算法實質上是一種特殊的PID控制算法，與傳統PID控制算法的不同之處是當姿態偏差較大時，在每個控制周期內只截取其中的一部分偏差進行控制，逐步消除姿態偏差，以實現小衛星逐漸逼近期望姿態的目的；當姿態偏差較小時，在每個控制周期內直接對該偏差進行控制，進而消除該偏差。

2.4.2.1 姿態指令分析

由于小衛星與上面級平臺分離后，需要對上面級平臺定向，所以，選取分離時刻的慣性坐標系作為姿態參考坐標系，定義分離時刻的慣性坐標系為oxdydzd，簡稱分慣系，以上面級分離小衛星時刻上面級體坐標系為分離慣性系，分慣系與上面級分離小衛星時刻上面級體坐標系ox1y1z1重合。

因此，小衛星要實現對上面級定向，需要將小衛星本體相對于分離慣性系的姿態四元數穩定在[1.0, 0.0, 0.0, 0.0]。考慮到小衛星在上面級平臺上安裝時，小衛星的本體坐標系與上面級的本體坐標系重合，小衛星與上面級分離時，上面級平臺的-y軸朝向地球，要使小衛星本體的z軸(安裝測控天線面)朝向地球，小衛星本體還需要繞其x軸轉動約90°(需要的最大轉動為90°)，為考核姿態控制系統的控制能力，所以，這里按照轉動90°進行設計與驗證，所以，小衛星的姿態四元數指令qc為[0.7071, 0.7071, 0.0, 0.0]，由于是對上面級平臺穩定定向，所以，姿態角速度指令ωc為[0, 0, 0]。

2.4.2.2 姿態控制律設計與穩定性分析

定義姿態四元數和姿態角速度指令分別為qc和ωc，姿態四元數偏差和姿態角速度偏差分別為：

?q

(12)

ωe=ω-ωc

(13)

由于姿態四元數存在歸一化約束，所以，只需對姿態四元數的矢部進行控制，設計姿態控制律如下：

Tc=-kpqev-kdωe+ω×h

(14)

式中，qev為姿態四元數偏差qe的矢部；kp為比例系數；kd為微分系數。

小衛星繞其3個主軸的轉動慣量分別為Jx=0.6 kg·m2，Jy=1.2 kg·m2，Jz=1.12 kg·m2。結合小衛星的姿態運動學與動力學模型，設計三軸姿態控制參數。

下面通過控制系統的bode圖和根軌跡圖來分析控制系統的穩定性。通過使用Matlab軟件，得到應用PD控制算法時的姿態控制系統的三通道bode圖分別如圖1、圖2和圖3所示，小衛星的轉動慣量由原來的80%變化到120%時，姿態控制系統的三通道根軌跡圖分別如圖4、圖5和圖6所示。

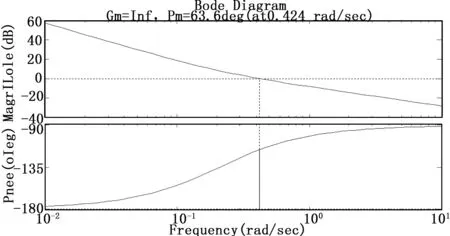
圖1 滾轉通道的開環bode圖

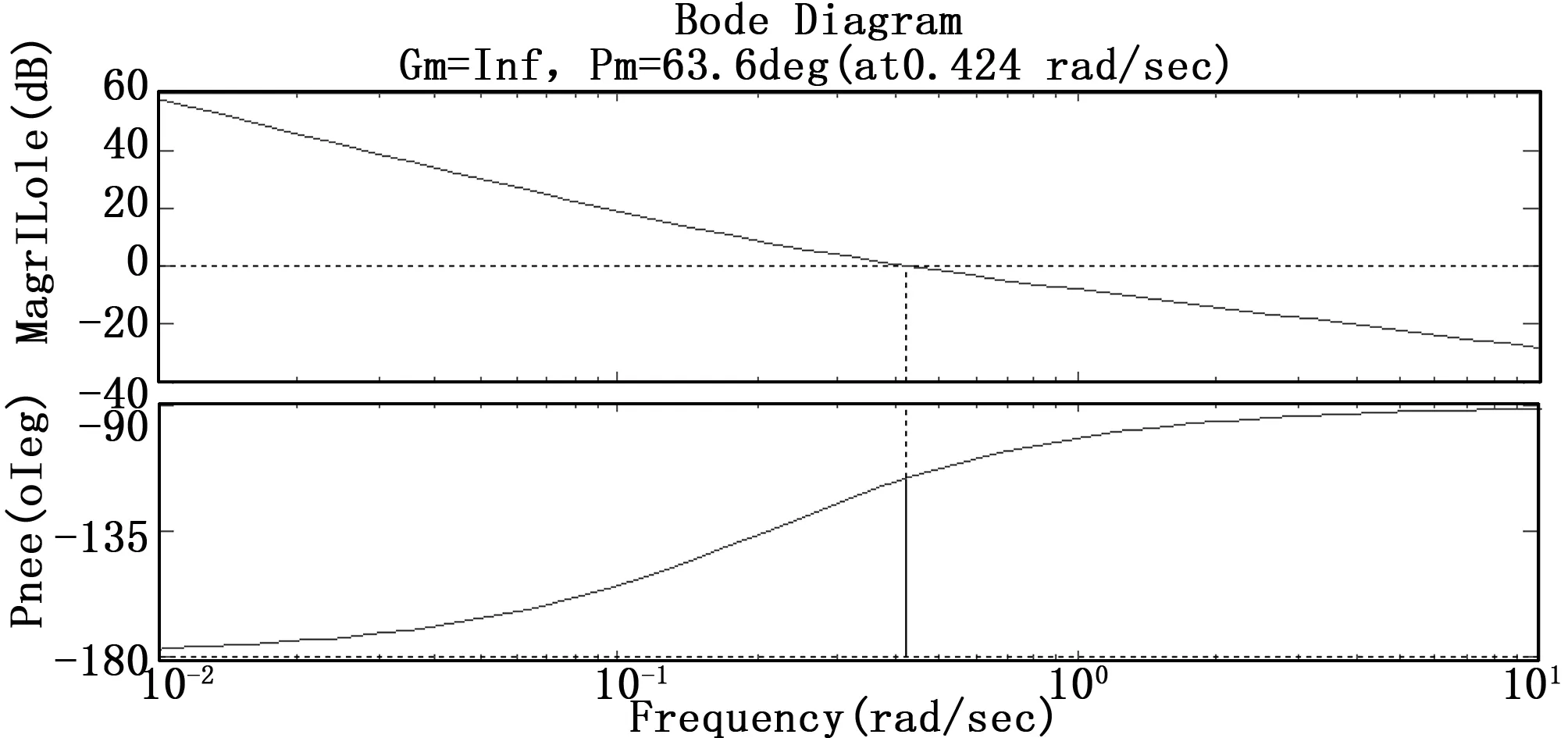
圖2 俯仰通道的開環bode圖

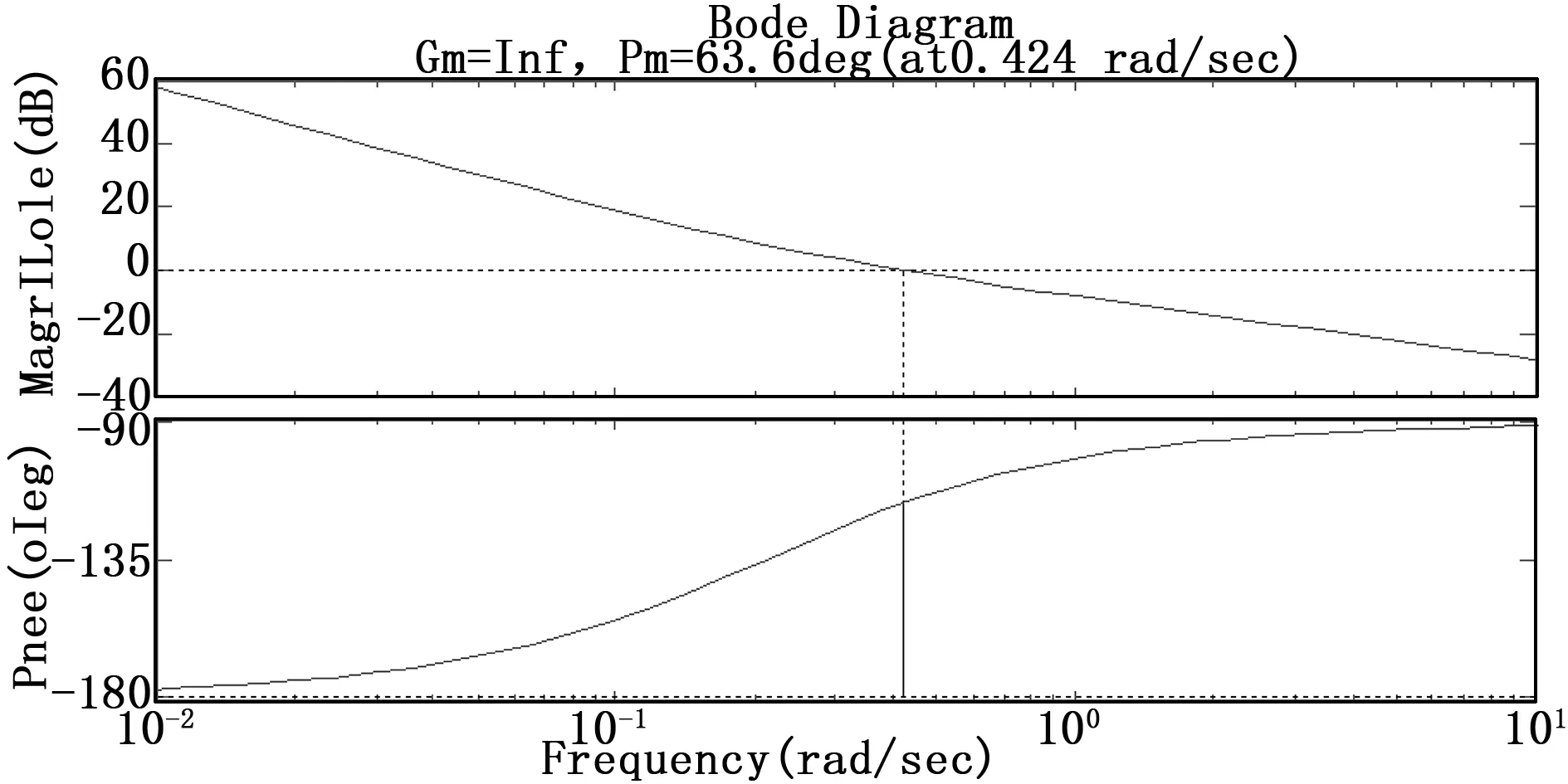
圖3 偏航通道的開環bode圖

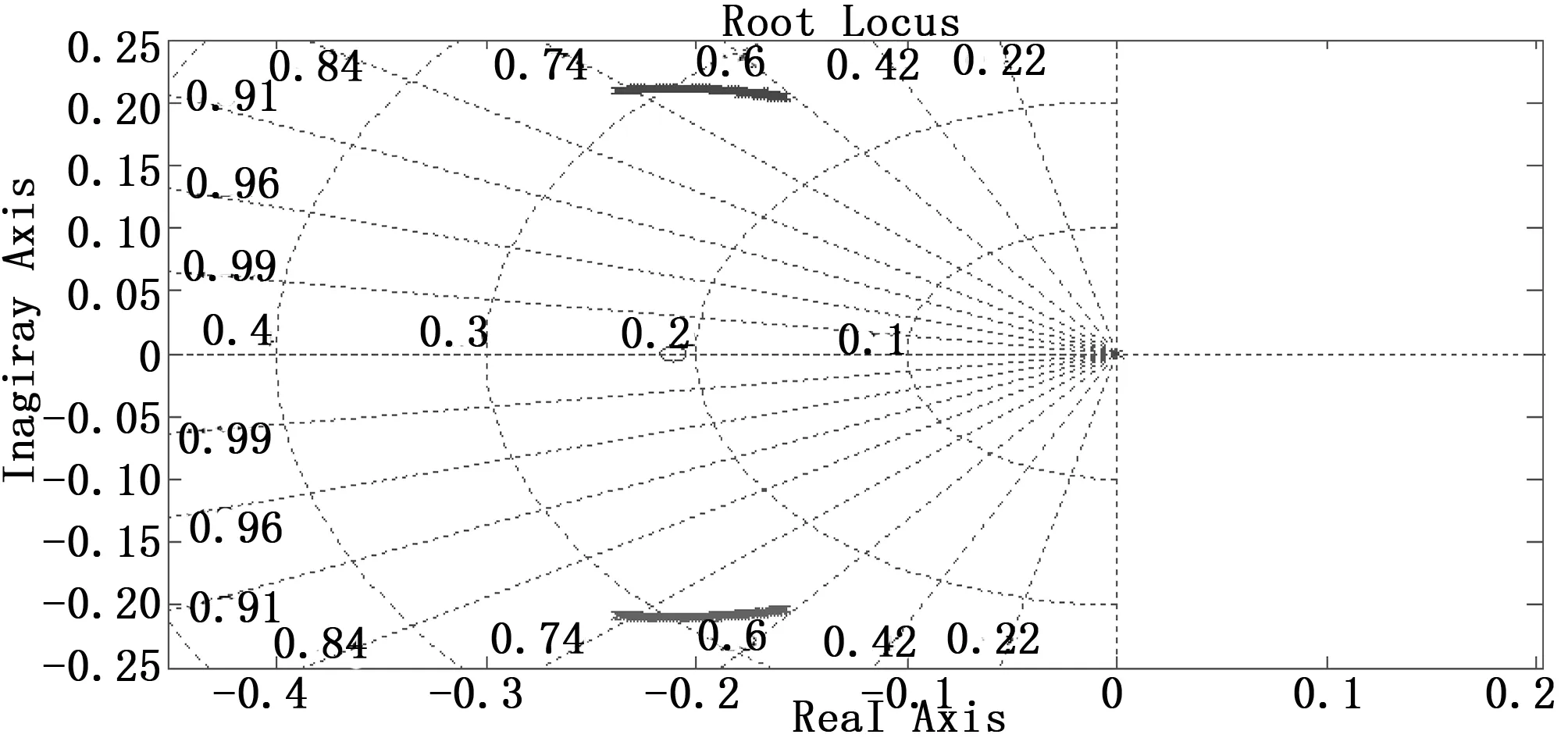
圖4 滾轉通道的根軌跡圖

圖5 俯仰通道的根軌跡圖

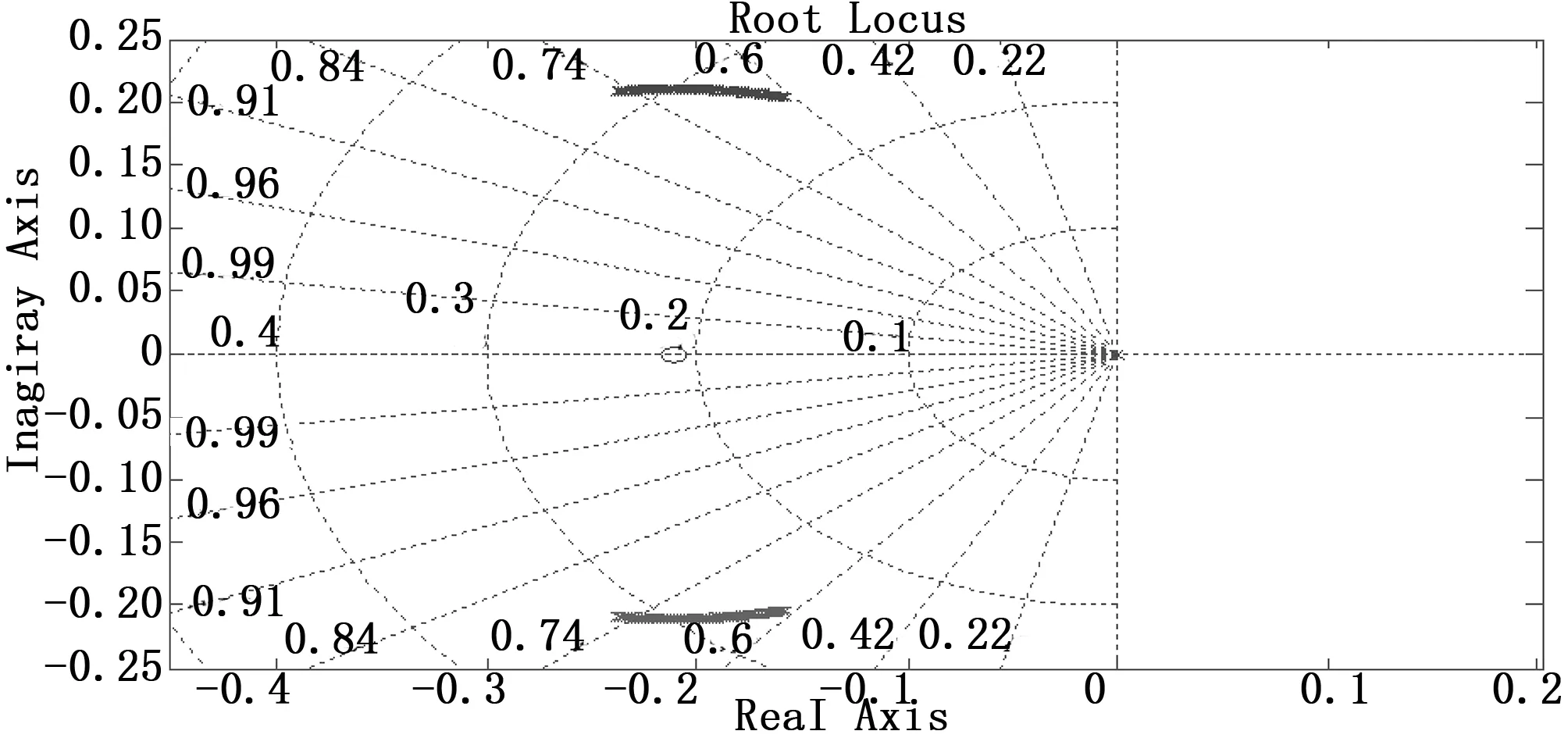
圖6 偏航通道的根軌跡圖

由圖1、圖2和圖3可知，設計的滾轉、俯仰和偏航三通道的幅值裕度為正無窮，相位裕度為63.6°。由圖4、圖5和圖6可知，當小衛星的轉動慣量由原來的80%變化到120%時，滾轉、俯仰和偏航三通道的閉環極點都在左半平面內，并且距離虛軸有一定的距離，所以，小衛星的轉動慣量變化在±20%范圍以內時，上述設計的姿態控制系統是穩定的。

2.4.2.3 姿態四元數偏差限幅

對姿態四元數偏差的矢部進行限幅，具體表達式如下：

(15)

式中，ke=‖qev‖∞；qemax為姿態四元數偏差的限幅值。

2.4.3 控制力矩限幅

根據飛輪的安裝，可得每個飛輪的力矩指令為：

Tcwheel=DwheelTc

(16)

式中，Tcwheel為每個飛輪的力矩指令；Dwheel為飛輪分配矩陣。

由于飛輪的最大輸出力矩有限，為了保證控制系統的跟蹤性能，對控制力矩進行限幅處理，使用飽和函數的方式對積分項進行限幅，具體如下：

(17)

式中，kT=‖Tcwheel‖∞；Tcmax為飛輪可提供的最大輸出力矩。

2.4.4 生成轉速指令

由于通過設計控制算法得到的指令為控制力矩指令，對于轉速反饋式飛輪，其接收的指令是轉速指令，所以，當選取轉速反饋式飛輪為姿態控制的執行機構時，需要將控制力矩指令轉化為轉速指令，具體如下。

(1)形成角動量指令：

(18)

式中，H0為飛輪初始角動量，Ts為控制周期。

(2)形成轉速指令：

(19)

式中，Jwheel為每個飛輪的轉動慣量形成的對角陣。

(3)轉速指令限幅：

(20)

式中，ωwheelcj為第j個飛輪的轉速指令，ωwheelcmax為飛輪的最大轉速，kwheel為安全系數。

3 仿真驗證

為了驗證上述設計的姿控方案、定姿算法、姿控算法，開展姿控系統的數學仿真與半實物仿真，具體仿真情況分別如下。

3.1 數學仿真驗證

根據上述設計的定姿算法與控制算法，使用C語言編制姿控的箭上程序(算法)，并使用Matlab/Simulink搭建小衛星的姿態運動學與動力學模型、陀螺測量模型、反作用飛輪模型、軌道模型、干擾力矩模型(主要考慮氣動干擾力矩、重力梯度干擾力矩、普遍的常值干擾力矩與周期性干擾力矩)，進行了多種初始狀態下的數學仿真。現給出其中一種工況下的仿真結果，分離時姿態角速度為[3,-3,3]°/s，期望的姿態四元數為[0.7071, 0.7071, 0.0, 0.0]，飛輪最大角動量為0.3 N·m·s，飛輪最大轉速為±6 000 rpm，仿真800 s，仿真結果如下：

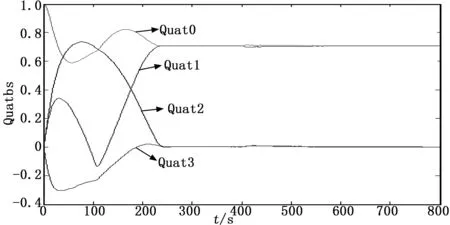
圖7 姿態四元數

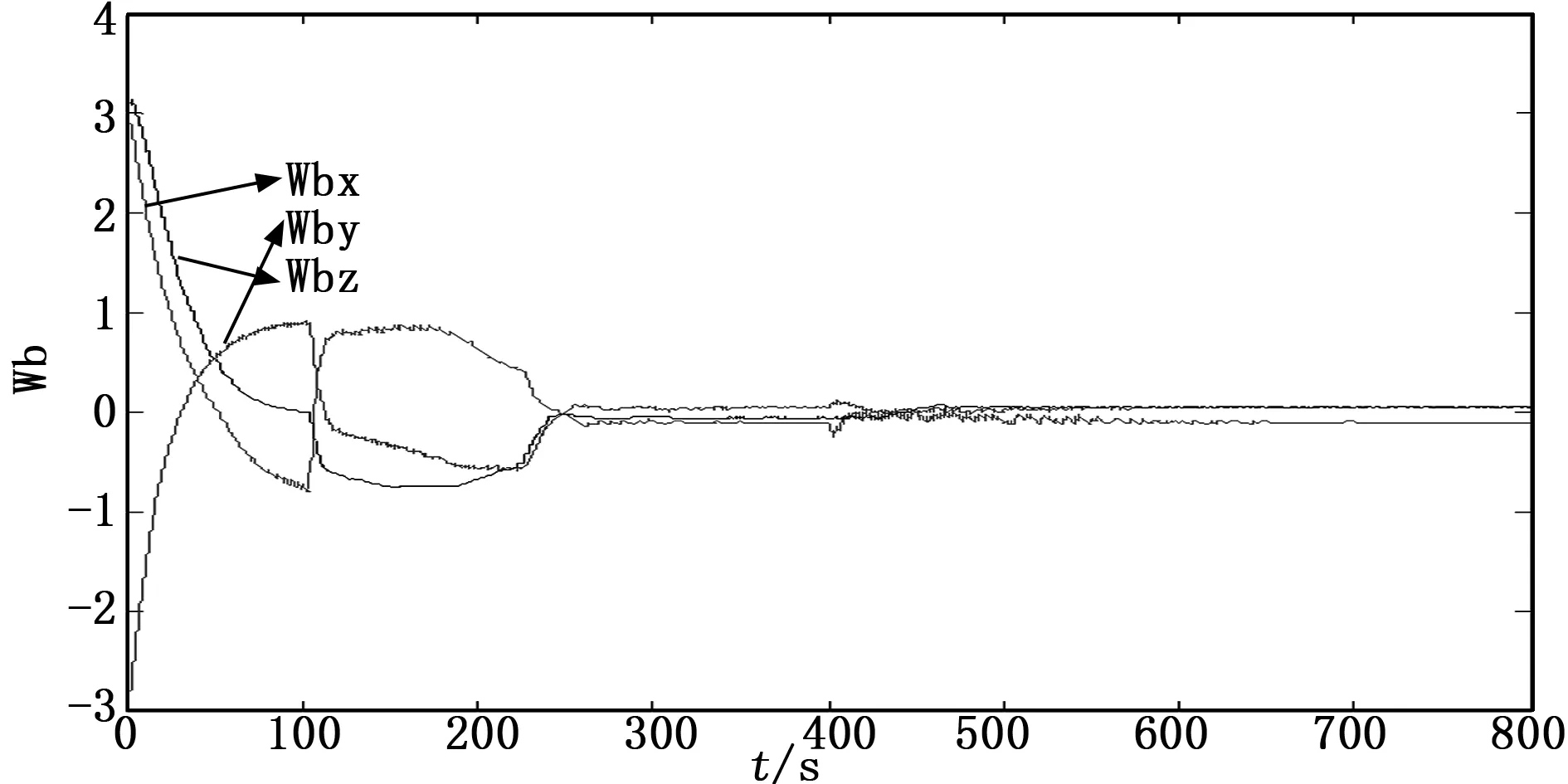
圖8 姿態角速度

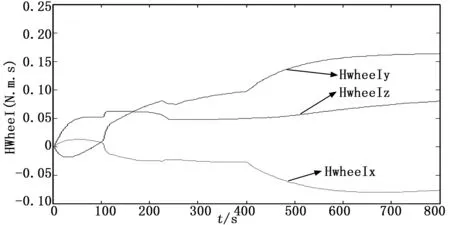
圖9 飛輪角動量

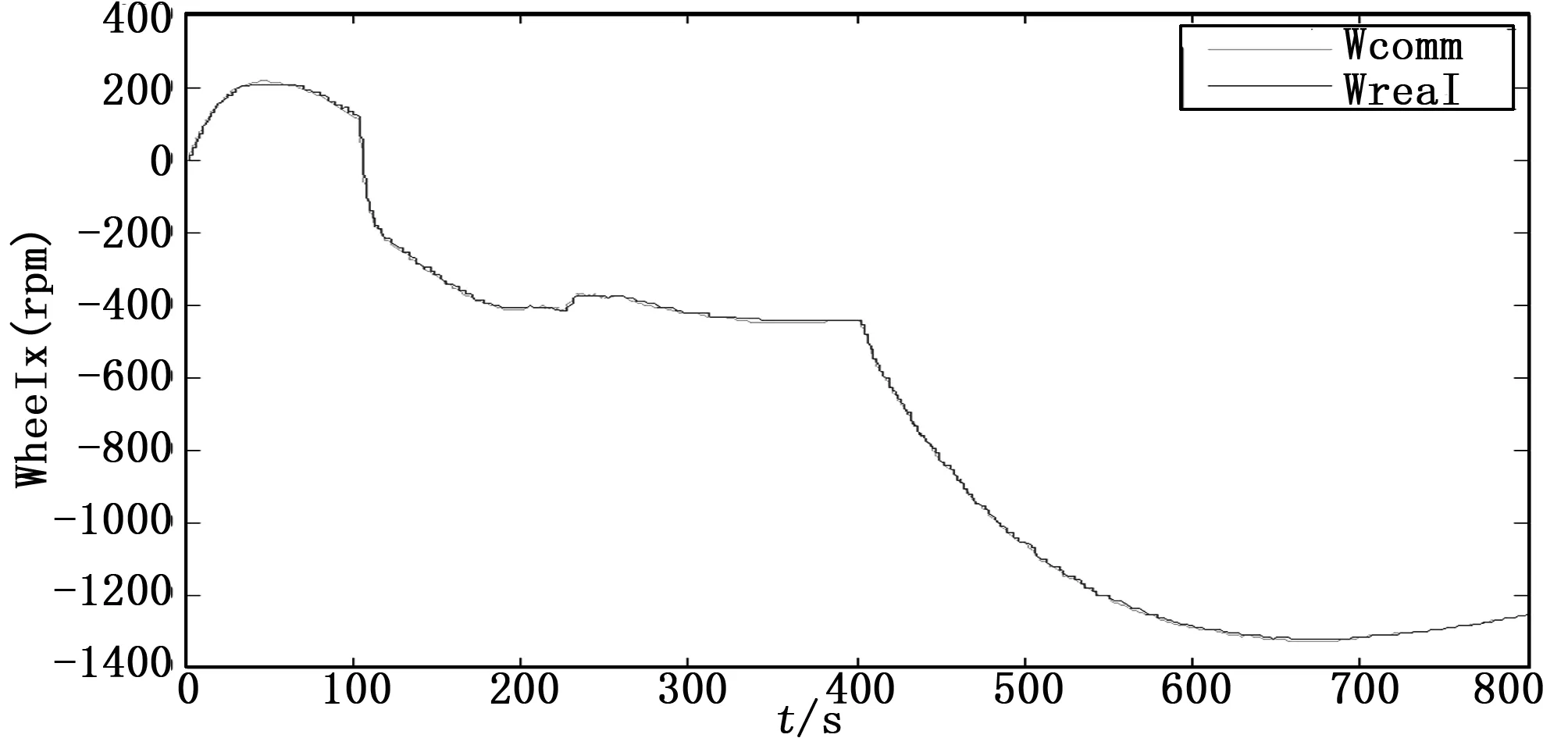
圖10 軸飛輪轉速

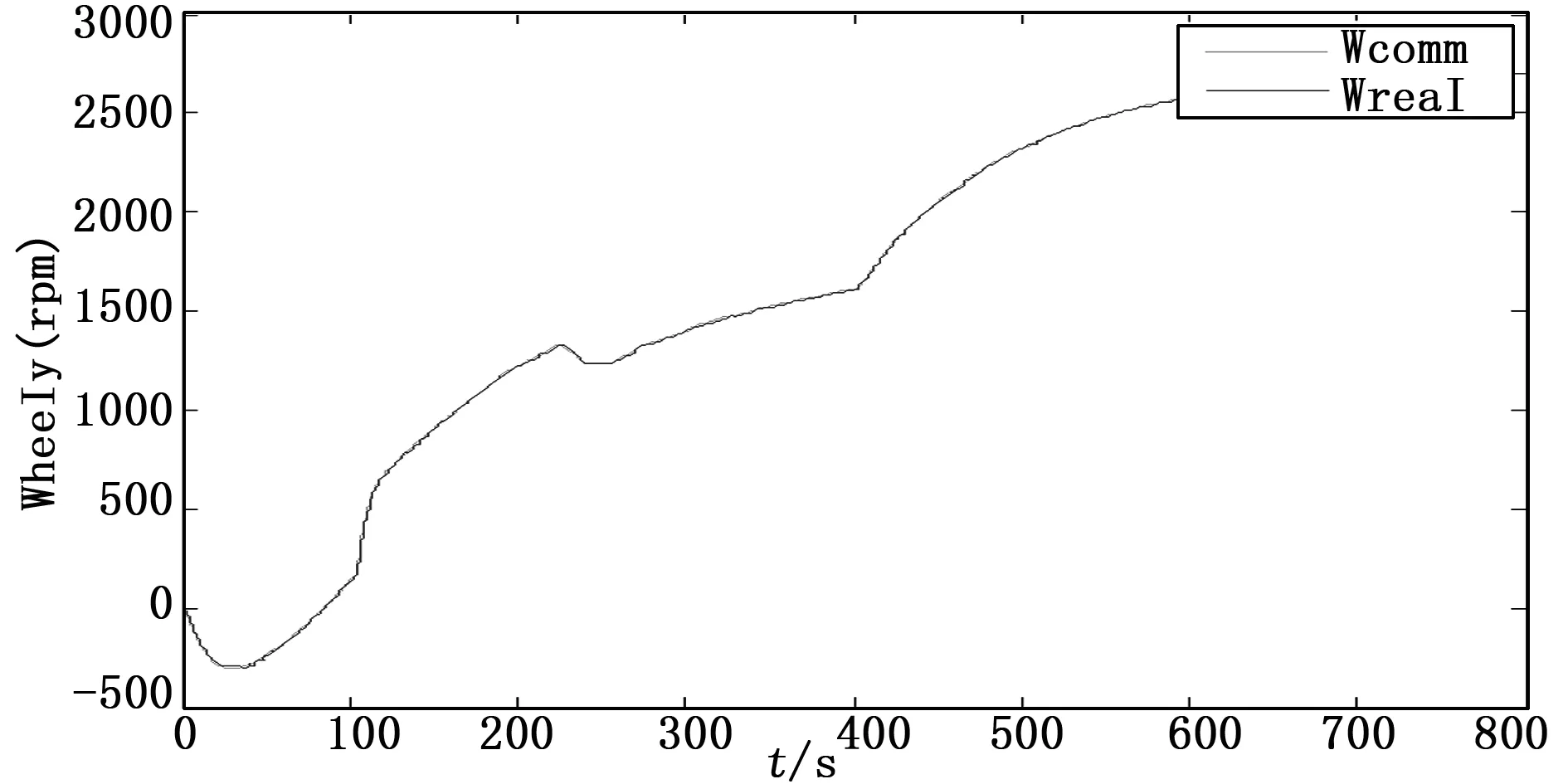
圖11 軸飛輪轉速

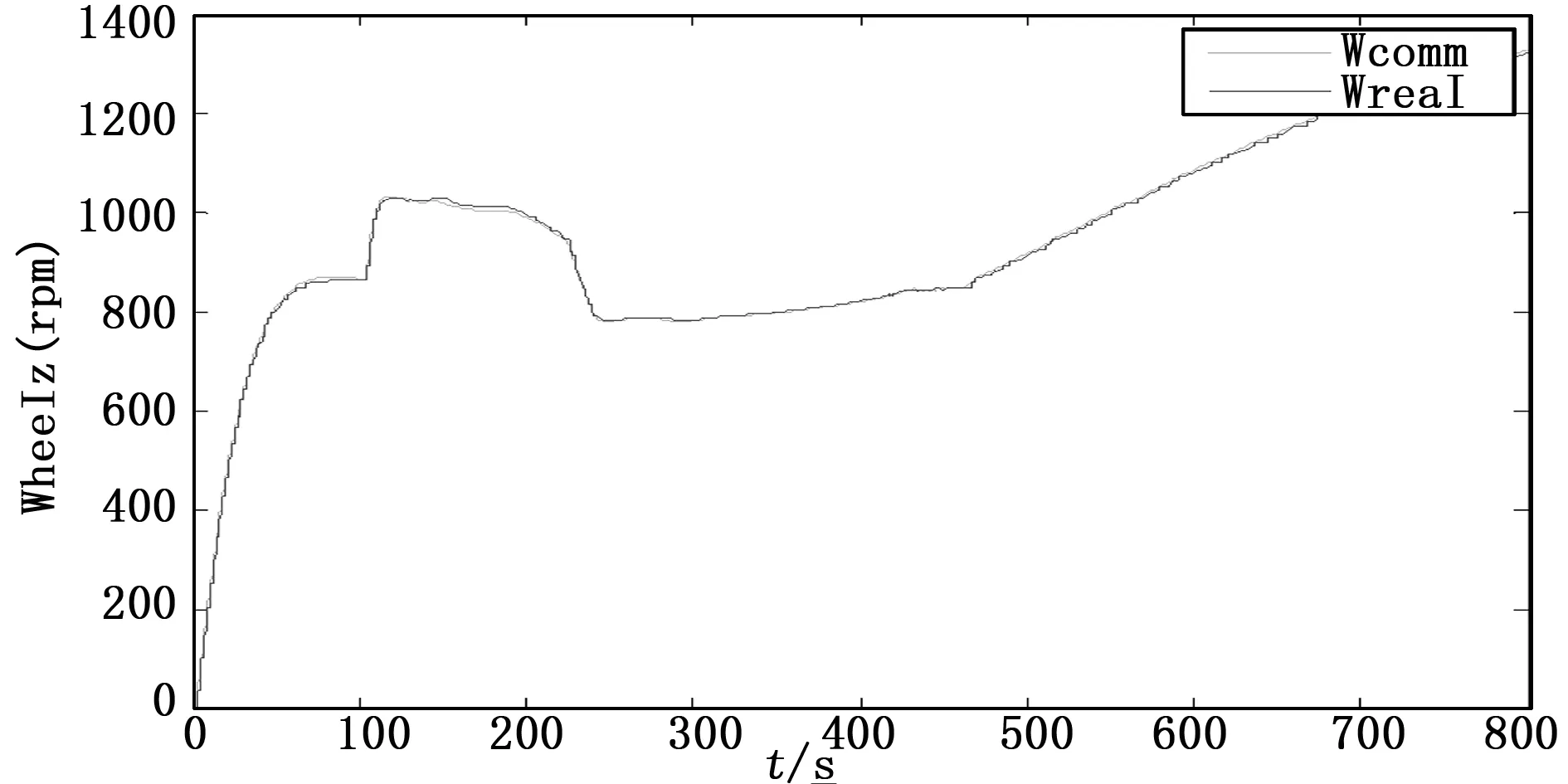
圖12 軸飛輪轉速

根據上述仿真結果，小衛星本體相對于分離慣性系的姿態在240 s左右穩定，實現了對上面級平臺的定向。三軸飛輪的角動量最大不超過0.17 N·m·s，有一定余量，三軸飛輪的實際轉速也都跟蹤上了指令轉速。

3.2 半實物仿真驗證

在數學仿真的基礎上，搭建小衛星姿控系統的半實物仿真平臺，并開發相應的軟件。使用C語言編制任務管理軟件，通過任務管理軟件調用姿控程序，使用任務管理組合、實時仿真機、供配電單元、反作用飛輪等實物開展姿控系統半實物仿真。供配電單元為任務管理組合與飛輪供電，任務管理組合上運行任務管理軟件與姿控軟件，實時仿真機上運行小衛星姿態模型、陀螺測量模型和軌道模型、干擾力矩模型，半實物仿真示意圖如圖13所示。

圖13 小衛星姿控系統半實物仿真示意圖

小衛星姿控系統半實物仿真平臺搭建完成，相關軟件完成開發調試后，開展小衛星姿控系統的半實物仿真，主要進行了兩類半實物仿真，一類是飛輪開環跟蹤的姿控系統半實物仿真(主要驗證飛輪的動態跟蹤性能)，另一類是飛輪閉環跟蹤的姿控系統半實物仿真(主要驗證姿控系統功能與性能、重點驗證姿控算法)。飛輪開環跟蹤為姿控系統使用飛輪模型進行閉環控制，飛輪接收轉速指令進行轉速跟蹤，但飛輪實際轉速不接入姿控回路。飛輪閉環跟蹤為飛輪實物接入姿控回路，飛輪接收轉速指令進行轉速跟蹤，同時將飛輪的實際轉速接入姿控回路，并根據飛輪實際轉速生產控制力矩，作用在小衛星的姿態動力學模型上。分別對這兩類情況進行了大量的半實物仿真，選取與上述數學仿真初始狀態同樣的仿真情況。

由飛輪開環跟蹤的姿控系統半實物仿真結果可知，小衛星姿態穩定，距離分離時刻240 s左右實現了對上面級平臺的定向，3個飛輪的轉速跟蹤正常。由飛輪閉環跟蹤的姿控系統半實物仿真結果可知，小衛星與上面級平臺分離后實現了姿態穩定，并在距離分離時刻240 s左右實現了對上面級平臺的定向，驗證了姿控算法的正確性，3個飛輪的轉速跟蹤正常。飛輪閉環跟蹤曲線與飛輪開環跟蹤曲線趨勢一致，在時間轉速上略有差別。最后對實際飛行試驗結果分析，姿控系統設計正確，滿足技術要求。

4 結論

本文研究了小衛星對上面級定向的姿控系統，設計了小衛星對上面級定向的姿控方案，針對小衛星對對上面級快速定向與對地數傳的問題，設計了基于陀螺的4階龍格庫塔積分算法與遞階飽和PD控制算法，并通過數學仿真對設計的姿控方案、姿控算法進行了初步驗證。在此基礎上，搭建了小衛星姿控系統半實物仿真平臺，進行了飛輪閉環跟蹤的小衛星姿控系統半實物仿真，進一步驗證了姿控方案、姿控算法設計的正確性。最后經過飛行試驗，對實際飛行結果分析，證明了姿控系統設計的正確性。