退無可退，方是進矣

張凌云

背景

一所農村學校，初中三個年級共6個班，每個年級2個班。因為師資缺乏，任教數學學科的三位教師均非數學專業科班出身。該校初二年級的數學期考平均分低于同區同年級平均分20分左右。此次筆者任教的就是初二年級其中的一個班，原本是應該班數學教師的要求上一節“平面直角坐標系”的概念課，結果所發生的事情有點超乎想象。

教學過程還原

環節一：

問題引入：請同學們回憶一下我們學過的數軸。可以用自己的語言描述。

因為引入的問題簡單，認為應該是信心滿滿的運籌帷幄，學生卻給了我一個下馬威！沒一個學生舉手回答問題，甚至于豎著耳朵想“捕風捉影”，結果連學生小聲議論的聲音都沒抓到。學生面面相覷，有欲言又止的，叫起來回答，卻說不出話。說不出來嚴謹概念沒關系，讓學生用自己的語言表達，也沒有，那讓學生畫圖，竟也沒人動手與附和。一點想法都沒有？確實尷尬！僵持了一陣，頭腦里一直在轉悠，怎么辦，如何處理？（說實話，挺尷尬的，后面老師在聽課，自己都懷疑該如何下臺了。）

不得已，改變策略，問：數軸，先是“數”，用“數”字組詞？你能夠組出哪些詞語？

于是學生開始陸陸續續回答：數字，整數，分數，正數，負數，小數，自然數，代數，有理數，無理數，……（好，一一肯定，正中下懷了，學生基本把數軸上的點能表示的數都說出來了！）

繼續問：那么“軸”呢，怎么理解？

學生：一條線，一條直線，一條水平的線……（不錯！）

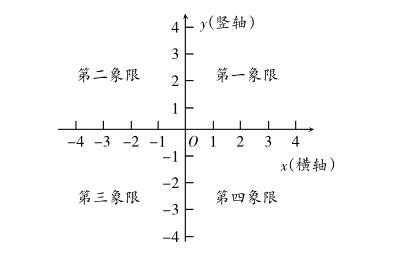
這時，終于有一個學生舉手了：想起來了，我可以畫。于是請他上講臺，其他的學生結合“數”“軸”二字的含義，畫出印象中的數軸。（一直在想，如何讓學生從文字中就能大致看懂數學概念，從文字中讀懂數學題目隱含的信息，于是在教學中偶爾也會有意識的教學生“咬文嚼字”，從字面上先去感悟，再回到嚴謹的數學表達。）

學生畫得不錯，圖形上面明確標出數軸的原點、正方向和表示單位長度的數字。

就著學生的圖，我講解數軸的三要素，數軸上的點的表示，以及數軸的特點，原點分界，從左到右逐漸增大。連帶相反數，絕對值（代數和幾何意義）都給學生講了一遍。想法也就是讓學生通過回憶能在后續的平面直角坐標系的學習中進行關聯：原點分界對應平面直角坐標系中的軸分界，相反數則對應于平面直角坐標系的對稱性，絕對值則對應平面直角坐標系中點到各坐標軸的距離。

終于可以從數軸上的點引入到平面上的點了！

環節二：

讓學生觀察生活中的實例，如座位的排列，圍棋的棋譜記錄，以及地理位置的經緯度表示等。

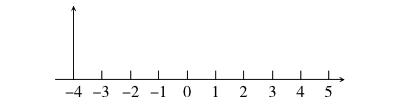
提問：如果點不在數軸上，而是在平面上，那該怎么表示？我特意在數軸上的數字1下方點了一個點（如下圖）。

生：還是1。

真是難不倒你們？！如果我繼續打點，學生難道會一直說1嗎？終于有學生說不行，可以再畫一條直線，那么怎么畫？

請學生在提供的方格紙上嘗試表達平面上的點的方法，也就是加一條垂直的軸進去。另請一主動舉手的學生上黑板在已有的數軸上畫圖。

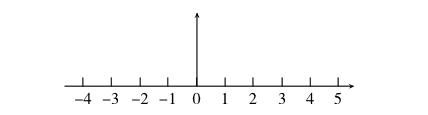
只是令自己沒想到的是，加一條縱軸，學生竟直接在數軸的最左邊畫上去（如下圖），在學案上畫圖的學生大部分只畫出了第一象限。又怎么辦？（黑板上的錯誤不能一擦了之啊！自己是一個頭兩個大了。）

讓學生先行觀察上圖。

接著問：兩條軸的交點怎么標數？

生：-4。

師：那往左邊走，怎么標，往上走呢，又怎么標數字？

學生停頓了，看著黑板，看表情應該是覺得有點不對勁的感覺，也就是說往上總不至于標“-5”吧，于是提出要進行調整。

師：那你覺得應該怎么調？

生：把豎的那條線移到原點的位置。

師：你們同意嗎？

學生都沒有再提出異議，于是此時移動豎直方向數軸到原點處。

師：這時豎直方向數軸上的點又如何標數呢？

故意從上往下標1，2，3，學生紛紛喊不行，要從下往上標，自然確定了縱軸的正方向。那么下方的點怎么辦呢？又自然將縱軸向下延伸，標上-1，-2，-3…。

平面直角坐標系完整建立，隨后的象限，象限內點的坐標符號特征都水到渠成了。