創(chuàng)新,在不知不覺中發(fā)生
黃城紅


人教版數(shù)學教材五年級下冊練習二十二中有一道題目(如圖1所示),學生解答第一小題時,出現(xiàn)了意外的驚喜。
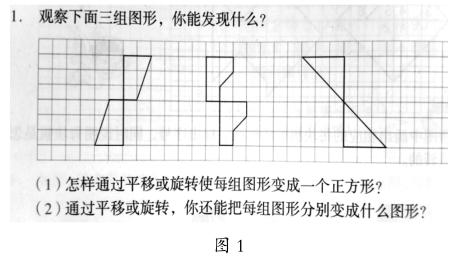
對第一個圖形,學生很容易想到利用平移就可以變成正方形。對第二個圖形,學生也能想到通過平移和旋轉把它變成正方形,得到下面的兩種方法。
方法一:(如圖2)以P點為中心,將上面這個圖形順(逆)時針旋轉180度,再向右平移2格,就能拼成正方形。
方法二:(如圖2)以M點為中心,將下面這個圖形順(逆)時針旋轉180度,再向左平移2格,也能拼成正方形。
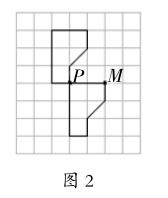

這兩種方法在旋轉時,都是利用圖形中已有的兩條邊線的交點作為旋轉中心,由于點比較醒目,學生容易發(fā)現(xiàn)。但在教學過程中,有一個學生想到了這樣的方法(如圖3):以N點為中心,只要把下面這個圖形順(逆)時針旋轉180度,一步就可以得到答案。
這種方法非常簡便,很有創(chuàng)意!能想出這個方法的學生思維確實很獨特!當該生講完自己的思路時,教室里響起了熱烈的掌聲。筆者聽到這個方法也覺得意外,因為把N點作為旋轉中心,學生是不容易發(fā)現(xiàn)的,可以說,這個旋轉中心是學生為了旋轉變換的需要特意想出來的。筆者在課后反思中發(fā)現(xiàn),這個創(chuàng)新性想法的出現(xiàn)與上一節(jié)課教學的這道開放題有著密不可分的聯(lián)系。
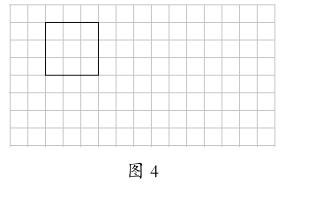
題目:(如圖4)請先把正方形向右平移6格,再順時針旋轉90度。
學生動手獨立完成。我在巡視時發(fā)現(xiàn)學生有多種方法,與我設計這道題的目的相吻合。在講評時,我讓學生展示了各自不同的方法。
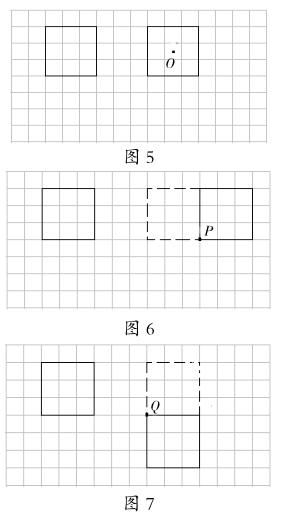
生1:我是先把正方形向右平移6格,再以O點為中心順時針旋轉90度。由于O點是正方形的中心,所以繞著O點順時針旋轉90度后的正方形與旋轉前是一樣的(如圖5)。
生2:我是先把正方形向右平移6格,再以P點為中心順時針旋轉90度的(如圖6)。
生3:我是先把正方形向右平移6格,再以Q點為中心順時針旋轉90度的(如圖7)。
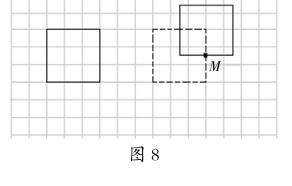
生4:我是先把正方形向右平移6格,再以M點為中心順時針旋轉90度的(如圖8)。
生5:老師,我對生4的“以M點為中心旋轉”有疑問。
生4:就是以M點所在的豎邊為標準,原來是豎著的方向,現(xiàn)在順時針旋轉90度后,這條邊變成橫向的了,同時整個正方形也沿順時針方向旋轉90度。
他說完,以一本封面接近正方形的本子為教具,示范了旋轉的方法。
師:通過生4的演示,大家就能更好地理解了。咦,這些同學得到的答案都不一樣,他們說的都有道理嗎?
生:他們說的都對。
師:為什么會有這么多不同的答案呢?
生6:因為題目中沒有規(guī)定旋轉的中心。
師:通過這道題的解答,你有什么體會?
生7:以不同的點為旋轉中心,所得到的圖形也是不一樣的。所以我們在對圖形進行旋轉變換時,一定要抓住旋轉變換的三要素:旋轉中心、旋轉方向、旋轉角度。
因為這道題目沒有說明以哪個點為旋轉中心,答案就會各不相同。學生在平移、旋轉的過程中,自然而然地體會旋轉中心是圖形在旋轉變換時不可或缺的一個要素,對旋轉中心不同會引起不同的結果有了切身的體會。
教學感悟:
我們在課堂上,總希望學生有創(chuàng)新性思維,也覺得這種創(chuàng)新性想法是少數(shù)學生的專利。但筆者認為,創(chuàng)新確實需要靈感,但它并不是空中樓閣,而是需要有深厚的認知基礎。只有每個學生夯實了自身的認知基礎,創(chuàng)新才成為一種可能。
這次的教學經(jīng)歷讓我收獲了很多。我很慶幸自己設計了一道沒有規(guī)定旋轉中心的開放題。在設計之初,我只是想讓學生對旋轉的三要素有更深入的理解,培養(yǎng)學生的開放性思維能力。但學生通過開放性的練習,思路被打開,發(fā)現(xiàn)不按常規(guī)來思考,可以找到多個旋轉中心,需要考慮各種不同的結果,這就為創(chuàng)新提供了可能。而解決教材中的這道題時,學生自覺將解決開放題的思維方式和方法遷移過來,創(chuàng)新性想法就自然產生了。可以說,這個創(chuàng)新性想法建立在學生深厚的認知基礎之上。這樣看來,教師在教學中,要幫助學生積累知識和經(jīng)驗,引導學生將知識進行聯(lián)系、整合,為學生的創(chuàng)新性思維提供基礎。
這也告訴我們,教育就是播種,它讓學生的思維自然生長,也許當時并不能看到結果,但學生經(jīng)過學習,有了一定的積淀,到了合適的時機就會自然地顯現(xiàn)出來。教育是一個慢過程,需要無痕的積淀。我們老師要做的,就是把學生的認知基礎打好,鼓勵學生的創(chuàng)新性想法,也許不經(jīng)意間,創(chuàng)新就會出現(xiàn)。
(作者單位:江西省南昌市鐵路第一小學)

