剛度矩陣和質量矩陣在民用飛機振動分析中的應用和驗證

任永鋒，嚴 玲，于江成

（上海飛機設計研究院，上海 201210）

0 引言

民用飛機機載設備數以萬計，接口界面多。如何準確定義邊界條件，對機載設備或者子結構進行準確的強度分析，尤其是振動分析，至關重要。

采用主結構模型進行連接分析最為準確，但由于飛機模型大，單元數量多，將飛機模型作為子結構強度計算模型導致計算模型龐大，且對分析設備要求高，耗時長[1]。另外，由于民機設計的界面分工問題，無法將主結構模型提供給機載設備供應商。雖然可以使用靜剛度和動剛度的分析方法提供界面剛度，但對于界面點多，邊界點自由度多的情況，提取過程繁瑣，且對于使用者而言，需要重新恢復剛度進行建模，導致易出錯，并且喪失了界面質量信息。因此，對于民用飛機多界面連接結構而言，如何準確提供界面的剛度矩陣和質量矩陣意義重大。

為解決復雜結構求解問題，20世紀60年代，Hurty提出了模態綜合的思想[2]，后經過Craig和Bampton的完善[3]，模態綜合法被逐步應用到工程計算中，形成了具有工程意義的子結構模態綜合法。90年代初，陳國平等將超單元法引入工程應用中，介紹了超單元內部的自由度縮減過程，并通過算例驗證了超單元法的精度[4]。超單元法可以縮減系統自由度，節省了計算時間，提高了計算能力[5]。

本文闡述了模態綜合超單元法基本原理，通過該方法計算得到了質量矩陣和剛度矩陣，并對子結構進行了模態分析，并和機體結構的分析結果、試驗結果進行了比較，驗證了該方法的正確性和可靠性。

1 模態綜合超單元法基本原理[6]

固定界面模態綜合法（CMS），即Craig-Bampton方法原理如下[3]：選擇適當的界面，將整個系統或結構分割成若干個子結構或部件。固定界面是假設子結構的界面全部被約束固定，通過界面坐標協調子結構之間的位移信息。模態綜合超單元法引入了基于精確動力縮聚的變換矩陣，能夠得到精度很好的系統動力學方程[6]。

將超單元的節點自由度分為邊界節點自由度B集和O集，從而超單元的質量矩陣和剛度矩陣可以表示為：

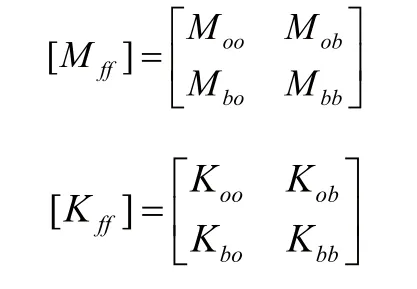
式中，[Mff]和[Kff]分別為超單元的質量矩陣和剛度矩陣。

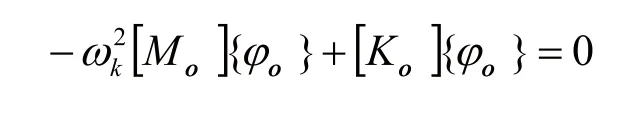
式中，[Koo]和[Moo]分別為超單元的剛度矩陣和質量和{φoo}分別為超單元邊界固定時的特征值和特征向量。

計算超單元的約束模態，即在單位邊界位移作用下的變形：

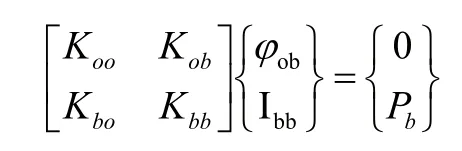
得到：

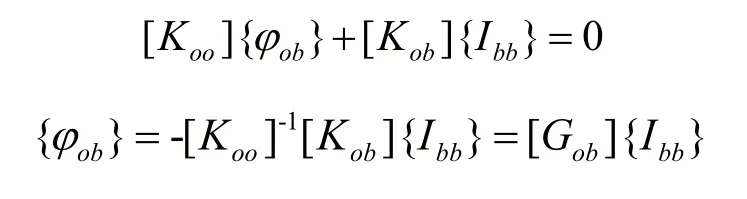
超單元在邊界約束下的模態可表示為：

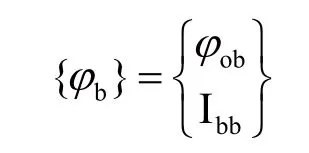
超單元假設模態由主模態和約束模態組成：

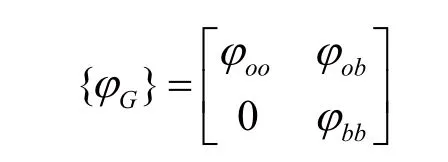
縮減后的超單元質量和剛度矩陣可為：

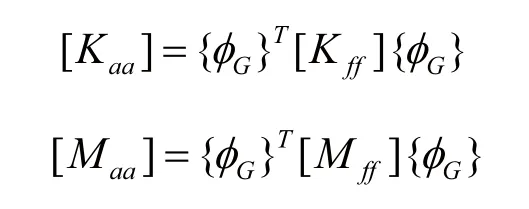
式中，[Maa]和[Kaa]分別為超單元的廣義質量矩陣和廣義剛度矩陣。

把超單元矩陣組裝到剩余結構上，得到整個結構的縮減矩陣方程，進而得到其動力學平衡方程，對總體結構進行求解[8]。

由于固定界面模態綜合法保留了所有的邊界自由度，所以收斂性好，計算精度高。在工程應用中可以通過減少子結構數目、減少對連接界面的復雜程度或采用分層多重動態子結構的方法來減少連接界面的對接自由度[9]，以實現準確而高效的縮減計算[6]。

2 模態綜合超單元法提取質量剛度陣

2.1 民用飛機某型連接結構介紹

民用飛行某型連接結構裝配如圖1所示，設備與主結構有3個連接點，分別是Point 1、Point 2和Point 3，連接結構如圖2所示。Point 3為單雙耳連接，Point 1和Point 2通過一中心銷軸連接。

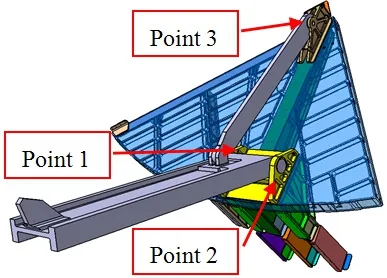
圖1 連接裝配圖

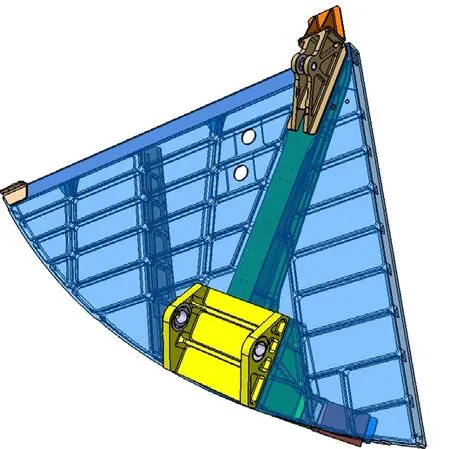
圖2 連接結構

2.2 有限元提取質量矩陣和剛度矩陣

圖1所示的結構分解為圖2所示的子結構以及剩余結構，對子結構的主要幾何模型，采用hypermesh軟件建立有限元模型，3個連接點建立rb2單元，分別建立相應的局部坐標系，具體的有限元分析模型如圖3所示。

在使用模態綜合超單元法提取剛度矩陣和質量矩陣動剛度時，在整體bdf有限元模型文件的Bulk Data Cards中加入一張參數卡：

PARAM, EXTOUT, DMIGPCH

另外，在整體bdf有限元模型文件的Bulk Data Cards中定義aset1 卡，以給出邊界點號及自由度。

ASET1，dof-num，node-num

其中，dof-num為自由度，node-num為節點編號。例如，

ASET1 123456 316805 356803 356806

通過Nastran軟件進行計算，生成的*.pch文件，即為剛度矩陣、質量矩陣和廣義坐標矩陣。

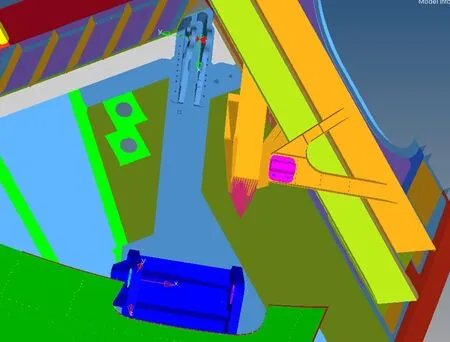
圖3 結構有限元模型

3 質量和剛度矩陣的使用及分析驗證

3.1 質量矩陣和剛度矩陣在分析中的使用

對于剩余的結構進行有限元建模分析，有限元模型如圖4所示。由于只對剩余結構進行分析，因此模型相對于整體模型而言，不論是分析的規模還是分析效率都將明顯提升。

圖4 剩余結構模型

在剩余結構模型的bdf文件SUBCASE中加入如下語句，來引用剛度和質量矩陣：

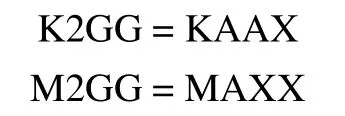
在bulk data卡中引用通過計算生成的包含邊界剛度矩陣和質量矩陣的pch文件：

BEGIN BULK

include '*.pch '

在模型中引用剛度矩陣和質量矩陣時注意以下幾點：

1）子模型中計算生成剛度和質量矩陣的邊界節點和剩余結構模型中邊界節點的節點編號必須一致；

2）子模型邊界節點和剩余結構模型邊界節點的坐標系必須一致；

3）引用的剛度和質量矩陣文件名稱必須和同文件夾內的真實文件名保持一致。

3.2 質量矩陣和剛度矩陣驗證

對剩余結構模型和整體結構模型使用Nastran的103求解器進行模態分析，前四階模態對比結果如表1所示。

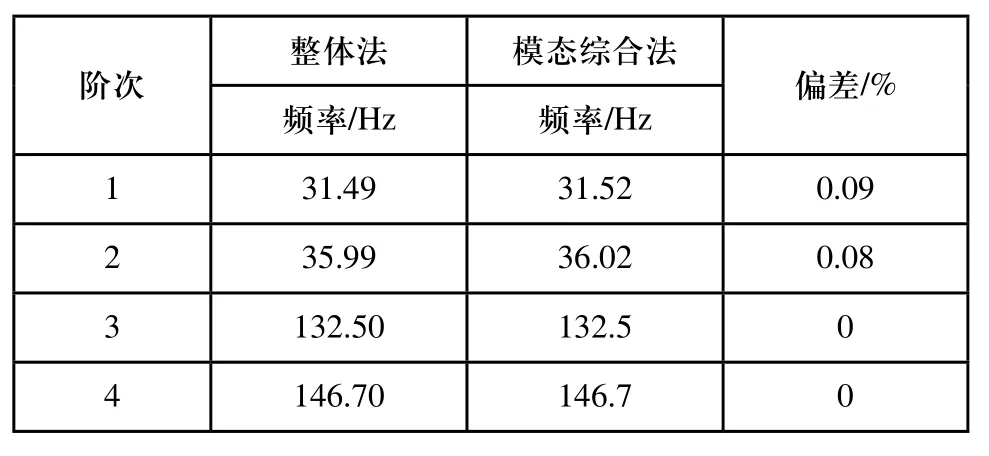
表1 模態分析結果對比

一階模態結果如圖5、圖6所示。

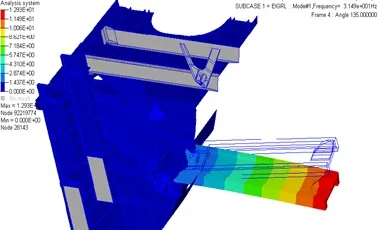
圖5 整體結構一階頻率

圖6 剩余結構一階頻率

通過以上對比看出，采用模態綜合超單元法提取的剛度矩陣和質量矩陣可以較準確的代替子結構，并用于代替子結構進行剩余結構分析，模態分析結果誤差在1%以內。

4 質量和剛度矩陣的使用及試驗驗證

上述子結構作為民用飛機某安裝結構，安裝某民用飛機設備（類似圖5，但非圖5），然后對機上該設備采用錘擊法進行模態試驗。在該設備上安裝三向加速度傳感器，并運用模態參數識別方法識別該結構的頻率、阻尼和陣型，1階陣型如圖7所示。

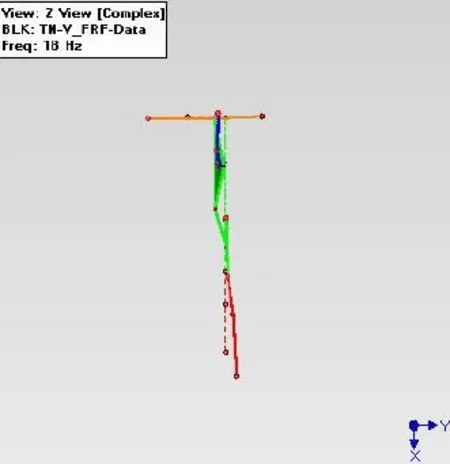
圖7 一階模態陣型和頻率

然后對使用子結構剛度和質量矩陣的設備模型進行模態分析，最終分析和試驗的模態對比結果如表2所示。

表2 模態試驗結果對比

通過以上對比可以看出，

1）低階頻率雖然偏差16.7%，但是實際上僅相差3Hz，考慮到模態試驗本身存在的誤差因素，分析結果已經較為準確。

2）對于其他頻率而言，采用模態綜合超單元法提取的剛度矩陣和質量矩陣可以較準確的代替子結構，并可用于代替子結構進行剩余結構的分析，和模態試驗結果誤差在5%以內，吻合度極高。

另外，對于偏差，原因可能來自：理論和實際本身有差異，連接條件理想化[10]，試驗中存在不確定因素等。

5 結論

本文詳細介紹了模態綜合超單元法和有限元分析提取和使用剛度和質量矩陣的方法，并對民用飛機某安裝結構進行了分析驗證，且通過錘擊法進行了模態試驗，進行了試驗驗證。得到結論如下：

1）采用模態綜合超單元法提取的剛度矩陣和質量矩陣可以較準確的代替子結構，并可用于代替子結構進行剩余結構的分析，模態分析結果誤差在1%以內。

2）使用模態綜合超單元分析方法提取得到的剛度和質量矩陣的模態分析結果和模態試驗結果誤差在5%以內，分析結果準確而有效。

3）使用模態分析超單元法可以減小分析模型大小，快速高效的進行強度分析和計算。

4）該方法可以用于其他多結構的連接分析中，對于民用飛機多界面問題而言是一個極其簡便且有效的方式。