基于相對(duì)熵方法的長(zhǎng)壽債券定價(jià)研究

宋平凡，譚常春，祁 毓

(1.合肥工業(yè)大學(xué)經(jīng)濟(jì)學(xué)院,安徽 合肥 230601;2.中南財(cái)經(jīng)政法大學(xué)財(cái)稅學(xué)院，湖北 武漢 430073)

1 引言

隨著生活水平的改善和醫(yī)療技術(shù)的進(jìn)步，我國(guó)居民的人均壽命正在大幅提高。根據(jù)世界銀行的數(shù)據(jù)顯示，我國(guó)居民的人均出生預(yù)期壽命由1990年的69.3歲上升到了2016年的76.2歲。人均壽命大幅改善是社會(huì)進(jìn)步的重要體現(xiàn)，但也給居民養(yǎng)老問題帶來了一定挑戰(zhàn)。尤其是計(jì)劃生育國(guó)策使我國(guó)的人口生育率降低，更加劇了人口老齡化問題。根據(jù)國(guó)家統(tǒng)計(jì)局發(fā)布的《2017年國(guó)民經(jīng)濟(jì)和社會(huì)發(fā)展統(tǒng)計(jì)公報(bào)》顯示，截至2017年末，我國(guó)60周歲以上的老齡人口占比為17.3%；65周歲以上的老齡人口占比為11.4%。如何應(yīng)對(duì)人口老齡化，如何解決養(yǎng)老問題，正成為當(dāng)前社會(huì)不得不正視的嚴(yán)峻現(xiàn)實(shí)。由于人口老齡化和居民壽命改善將使得養(yǎng)老金支出大幅增加，我國(guó)養(yǎng)老保障的“三支柱體系”均將面臨著隨之而來的財(cái)務(wù)沖擊。這種由于居民整體壽命改善而給養(yǎng)老基金或保險(xiǎn)公司帶來的財(cái)務(wù)風(fēng)險(xiǎn)被稱為長(zhǎng)壽風(fēng)險(xiǎn)。要想妥善處理居民養(yǎng)老所承受的資金壓力，就必須積極主動(dòng)地尋找科學(xué)管理長(zhǎng)壽風(fēng)險(xiǎn)的方法，這也與十九大報(bào)告提出的“實(shí)施健康中國(guó)戰(zhàn)略，積極應(yīng)對(duì)人口老齡化”的觀點(diǎn)相契合。

然而長(zhǎng)壽風(fēng)險(xiǎn)管理并非易事，由于保險(xiǎn)經(jīng)營(yíng)基本原理是運(yùn)用大數(shù)定律分散風(fēng)險(xiǎn)，但保險(xiǎn)公司和養(yǎng)老金機(jī)構(gòu)面臨的長(zhǎng)壽風(fēng)險(xiǎn)是不可分散的系統(tǒng)性風(fēng)險(xiǎn)，因而長(zhǎng)壽風(fēng)險(xiǎn)管理需借助其他渠道。目前被學(xué)界關(guān)注到的長(zhǎng)壽風(fēng)險(xiǎn)管理方法主要有兩種，一種被稱為自然對(duì)沖[1-3]，該方法是利用壽險(xiǎn)業(yè)務(wù)和年金業(yè)務(wù)現(xiàn)金流變化完全相反的特性，當(dāng)人均壽命增加時(shí)，通過壽險(xiǎn)業(yè)務(wù)的增值去對(duì)沖年金業(yè)務(wù)的長(zhǎng)壽風(fēng)險(xiǎn)。另一種引起學(xué)者關(guān)注的方案則是通過在資本市場(chǎng)發(fā)行金融衍生品(后文對(duì)該類衍生品簡(jiǎn)稱為長(zhǎng)壽衍生品)來對(duì)長(zhǎng)壽風(fēng)險(xiǎn)進(jìn)行對(duì)沖。在實(shí)踐中長(zhǎng)壽衍生品也有過先例，比較典型的是歐洲投資銀行(European Investment Bank)和法國(guó)巴黎銀行(BNP Paribas)聯(lián)合發(fā)行的長(zhǎng)壽債券(后文簡(jiǎn)稱EIB/BNP型長(zhǎng)壽債券)。該債券的發(fā)行雖然最終并未獲得成功，但作為典型長(zhǎng)壽債券實(shí)例，仍吸引了學(xué)者以之為對(duì)象展開研究。一些學(xué)者把EIB/BNP作為長(zhǎng)壽衍生品的典型案例進(jìn)行了分析[4-5]，但系統(tǒng)全面地介紹各類長(zhǎng)壽衍生品以及長(zhǎng)壽債券發(fā)行原理和特點(diǎn)的文獻(xiàn)至少可以追溯到Blake等[6-7]的研究。與一般金融衍生品的發(fā)行相似，長(zhǎng)壽衍生品發(fā)行的核心問題是定價(jià)。在該問題的研究過程中，學(xué)者們進(jìn)行了大量嘗試和探索，但各種定價(jià)方法也不可避免存在局限性。如Friedberg 和Webb[8]運(yùn)用資本資產(chǎn)定價(jià)模型(CAPM)和基于消費(fèi)的資本資產(chǎn)定價(jià)模型(CCAPM)來對(duì)長(zhǎng)壽衍生品進(jìn)行定價(jià)，但他們本人也承認(rèn)實(shí)際的風(fēng)險(xiǎn)市場(chǎng)價(jià)值要比使用該模型計(jì)算得到的結(jié)果高出許多；一些文獻(xiàn)提出了Sharpe比率法[9-10]，但該方法又被認(rèn)為本質(zhì)上趨同于市場(chǎng)風(fēng)險(xiǎn)價(jià)格為常數(shù)情形下的風(fēng)險(xiǎn)中性測(cè)度定價(jià)方法[11]； Wang[12-13]提出的“Wang轉(zhuǎn)換”方法雖然在長(zhǎng)壽衍生品定價(jià)領(lǐng)域得到一定應(yīng)用，但也被質(zhì)疑“并不能提供統(tǒng)一的理論框架”[14-15]。對(duì)于各種定價(jià)方法的原理和局限，已有部分文獻(xiàn)進(jìn)行了總結(jié)和比較[16-17]。一些研究也將經(jīng)典的風(fēng)險(xiǎn)中性測(cè)度理論引入到長(zhǎng)壽衍生品定價(jià)領(lǐng)域[18-21]，但在非完全市場(chǎng)中，風(fēng)險(xiǎn)中性測(cè)度Q并不唯一。為了解決這個(gè)問題，Li[22]使用了Kullback-Leibler相對(duì)熵方法(Kullback-Leibler relative entropy, 后文簡(jiǎn)稱KL相對(duì)熵, 有些場(chǎng)合也將相對(duì)熵稱作交叉熵，即cross entropy)。相對(duì)熵方法的引入從理論上解決了Q測(cè)度的選擇問題。這種方法在后續(xù)有關(guān)定價(jià)問題的研究中，也有了更多地應(yīng)用[21,23]。因此總體來看，在風(fēng)險(xiǎn)中性測(cè)度框架下使用相對(duì)熵方法是優(yōu)越性相對(duì)較高的一種選擇。

對(duì)長(zhǎng)壽風(fēng)險(xiǎn)衍生品定價(jià)而言，除了定價(jià)方法和定價(jià)理論的選擇，人群的死亡率進(jìn)行建模和預(yù)測(cè)也比較重要。早期的死亡率模型以靜態(tài)的模型為主，例如Gompertz模型[24]，Heligman和Pollard[25]提出的HP模型，還有Carriere[26]提出的CR模型等,該類模型的缺點(diǎn)是只考慮年齡因素而不考慮時(shí)間因素，適用于配合生命表進(jìn)行不同年齡死亡率的推算，但無法反映死亡率隨著不同年份的變化趨勢(shì)。Lee和Carter[27]提出了既考慮年齡因素也考慮時(shí)間因素的動(dòng)態(tài)死亡率預(yù)測(cè)模型，即Lee-Carter模型，在此之后，死亡率建模時(shí)主要采用的都是動(dòng)態(tài)化的模型，如Cairns等[28]提出的Cairns-Blake-Dowd兩因子模型(簡(jiǎn)稱CBD兩因子模型)。Lee-Carter模型主要用于不同年份的不同年齡群組整體死亡率的建模(如10-14歲群組)，CBD模型則可用于模擬不同年份具體年齡的人群死亡率，且對(duì)高齡人口的預(yù)測(cè)效果要更好一些。近期的相關(guān)死亡率建模開始關(guān)注到不同人群死亡率的相依性，例如Yang和Wang[29]使用向量誤差修正模型研究了不同國(guó)家人群死亡率的長(zhǎng)期均衡關(guān)系，還有一些研究使用了Copula方法去刻畫了不同人群死亡率相依性的研究[30-31]，但該類研究依賴于較長(zhǎng)期的歷史死亡率數(shù)據(jù)建模，目前還不具備使用我國(guó)數(shù)據(jù)進(jìn)行類似建模的條件。

總之，無論是定價(jià)方法還是死亡率預(yù)測(cè)模型的發(fā)展，都推動(dòng)了長(zhǎng)壽衍生品的研究，尤其是關(guān)于長(zhǎng)壽債券的研究。作為關(guān)注度較高的長(zhǎng)壽衍生品，長(zhǎng)壽債券有可能成為實(shí)踐中有力的長(zhǎng)壽風(fēng)險(xiǎn)管理工具。目前國(guó)內(nèi)的學(xué)者也開始重視我國(guó)的長(zhǎng)壽債券定價(jià)問題[32-37]。與EIB/BNP這種連續(xù)型的長(zhǎng)壽債券不同，國(guó)內(nèi)的研究大多構(gòu)造了類似期權(quán)原理的觸發(fā)式長(zhǎng)壽債券，這種債券的作用原理與Swiss Re在2003年底發(fā)行的死亡率巨災(zāi)債券原理相似， 但這種死亡率巨災(zāi)債券的初衷并非用來對(duì)沖長(zhǎng)壽風(fēng)險(xiǎn)，相反地，其用途主要是對(duì)沖極端災(zāi)害事件(如地震、海嘯和大范圍疾病)帶來壽險(xiǎn)業(yè)務(wù)的償付風(fēng)險(xiǎn)，但通過制定不同的標(biāo)的指數(shù)和觸發(fā)閾值，亦可構(gòu)造出形式相似但用于管理長(zhǎng)壽風(fēng)險(xiǎn)的債券。本文期望推動(dòng)長(zhǎng)壽衍生品定價(jià)研究的發(fā)展，并為我國(guó)長(zhǎng)壽風(fēng)險(xiǎn)的有效管理做出貢獻(xiàn)。本文所做的工作主要有：首先以歷年分年齡的死亡率數(shù)據(jù)為基礎(chǔ)，使用更適合高齡人口死亡率建模的CBD兩因子模型對(duì)未來不同性別人群的死亡率進(jìn)行模擬和預(yù)測(cè)；同時(shí)采用相對(duì)熵方法，并融合我國(guó)金融市場(chǎng)上所擁有的市場(chǎng)風(fēng)險(xiǎn)價(jià)值信息，對(duì)EIB/BNP型長(zhǎng)壽債券進(jìn)行定價(jià)。和之前的研究相比，本文可能的創(chuàng)新點(diǎn)有如下幾條：在研究?jī)?nèi)容上，本文以風(fēng)險(xiǎn)中性測(cè)度理論為框架，基于我國(guó)死亡率數(shù)據(jù)對(duì)EIB/BNP型長(zhǎng)壽債券進(jìn)行定價(jià)，同時(shí)，定價(jià)過程中也考慮了我國(guó)金融市場(chǎng)的風(fēng)險(xiǎn)價(jià)值信息，使長(zhǎng)壽債券定價(jià)的結(jié)果與我國(guó)人口死亡率情況和金融市場(chǎng)狀況更契合；在研究方法上，本文拓展了相對(duì)熵方法在長(zhǎng)壽衍生品定價(jià)領(lǐng)域的應(yīng)用，在求解最優(yōu)風(fēng)險(xiǎn)中性測(cè)度時(shí)不僅使用了KL相對(duì)熵，還使用了Tsallis相對(duì)熵以及Rényi相對(duì)熵方法，保證了計(jì)算結(jié)果的穩(wěn)健性；在對(duì)實(shí)證工作的總結(jié)上，與以往文獻(xiàn)不同，本文并非僅僅列出定價(jià)結(jié)果，而是更注重從實(shí)證結(jié)果中挖掘出我國(guó)長(zhǎng)壽風(fēng)險(xiǎn)所面臨的實(shí)際特點(diǎn)，以及在長(zhǎng)壽風(fēng)險(xiǎn)管理工作中需要注意的問題，可為長(zhǎng)壽風(fēng)險(xiǎn)管理提供有價(jià)值的參考建議。

2 EIB/BNP長(zhǎng)壽債券簡(jiǎn)介

限于篇幅，本文僅對(duì)EIB/BNP的債券定價(jià)發(fā)行和償付機(jī)制進(jìn)行簡(jiǎn)單介紹，該債券詳細(xì)的發(fā)行流程可見參考文獻(xiàn)[5]。歐洲投資銀行(EIB)和法國(guó)巴黎銀行(BNP)于2004年聯(lián)合發(fā)行了面值為5.4億英鎊，期限為25年的長(zhǎng)壽債券，該債券主要面向養(yǎng)老基金以及年金機(jī)構(gòu)，具有浮動(dòng)的息票支付，每年向投資者的息票支付為50,000,000×I(t) (單位：英鎊)，其中I(t)表示第t年的生存指數(shù)，該指數(shù)與特定人群的歷年死亡率掛鉤：

(1)

其中mx,t表示在第t年x歲的人群的死亡概率，t=0表示初始計(jì)息的前一年份。若在我國(guó)發(fā)行該類型債券，為方便討論，假定1×I(t)(單位：元)為息票支付，則該債券在0時(shí)刻的定價(jià)為

(2)

其中δ表示長(zhǎng)壽風(fēng)險(xiǎn)的溢價(jià)，代表長(zhǎng)壽風(fēng)險(xiǎn)的“市場(chǎng)價(jià)格”。需要指出的是，本文對(duì)長(zhǎng)壽債券進(jìn)行定價(jià)，實(shí)質(zhì)上就是計(jì)算不同期限長(zhǎng)壽債券對(duì)應(yīng)的風(fēng)險(xiǎn)溢價(jià)δ。Ft代表到時(shí)刻t為止的信息集，B(0,t)代表t時(shí)刻償付1元的零息債券以無風(fēng)險(xiǎn)利率(本文設(shè)定無風(fēng)險(xiǎn)利率為4%)貼現(xiàn)到0時(shí)刻的價(jià)格,表示在真實(shí)概率測(cè)度P下的數(shù)學(xué)期望。由于長(zhǎng)壽債券與特定人群的死亡率掛鉤，因此我們首先要獲得目標(biāo)人群未來死亡率的信息，本文以2017年64歲的男性和女性人群為目標(biāo)人群，為了構(gòu)造債券定價(jià)所需的生存指數(shù)，需要對(duì)目標(biāo)人群的死亡率進(jìn)行預(yù)測(cè)。

3 CBD兩因子模型

由于相比Lee-Carter模型而言，CBD兩因子模型對(duì)高齡人口的預(yù)測(cè)效果更好，而EIB/BNP型長(zhǎng)壽債券正是以高齡人群死亡率構(gòu)造生存指數(shù)的，因此本文采用了CBD兩因子模型建模，并對(duì)目標(biāo)人群的未來死亡率進(jìn)行模擬。

CBD兩因子模型的基本設(shè)定如下：在第t年時(shí)年齡為x的群體死亡率mt,x有如下性質(zhì)：

(3)

其中，二維列向量A(t)=(A1(t),A2(t))T服從二維的隨機(jī)游走過程

A(t+1)=A(t)+μ+C·Z(t+1)

(4)

其中，μ和C分別是漂移參數(shù)和擴(kuò)散參數(shù)，μ=(μ1,μ2)T為一個(gè)二維的列向量，C為2×2的下三角矩陣，Z(t)=(Z1(t),Z2(t))T是一個(gè)兩維的標(biāo)準(zhǔn)正態(tài)分布隨機(jī)變量,V-1和μ分別服從Wishart分布和多元正態(tài)分布：

(5)

在這里，V=CCT,即C是V的Cholesky分解,同時(shí)還有

D(t)～A(t)-A(t-1)

(6)

通過(4)-(6)式得到模型相關(guān)參數(shù)信息并模擬生成未來的死亡率因子A(t)，再通過(3)式進(jìn)行轉(zhuǎn)換即可得到目標(biāo)人群未來死亡率路徑。

4 最小相對(duì)熵方法

相對(duì)熵是衡量從一個(gè)測(cè)度轉(zhuǎn)換到另一個(gè)測(cè)度所獲得的信息增量。從貝葉斯統(tǒng)計(jì)學(xué)的角度來看，如果新加入的信息使原來的概率發(fā)生變化，那么新的概率測(cè)度的選擇應(yīng)當(dāng)盡可能產(chǎn)生最小信息增量，這也被稱作最小差別信息準(zhǔn)則(Minimum Discrimination Information)[38]。因而通過最小化相對(duì)熵我們能夠選擇與真實(shí)概率測(cè)度P信息量差距最小的風(fēng)險(xiǎn)中性測(cè)度Q。相對(duì)熵也有不同種類，如經(jīng)典的KL相對(duì)熵[39]，此外還有Tsallis相對(duì)熵[40]以及Rényi相對(duì)熵[41]。Li[22]使用KL相對(duì)熵研究長(zhǎng)壽債券的定價(jià)問題，而 Tsallis相對(duì)熵和Rényi相對(duì)熵也被用于金融定價(jià)領(lǐng)域，例如柳向東和王星蕊[42]以及Dolan等[43]的研究。實(shí)際上， Tsallis相對(duì)熵和Rényi相對(duì)熵包含了更多的參數(shù)，使得模型具有一定的靈活性，同時(shí)Tsallis相對(duì)熵和Rényi相對(duì)熵是KL相對(duì)熵的推廣，因而我們將其用于對(duì)KL相對(duì)熵方法計(jì)算得到的結(jié)果進(jìn)行穩(wěn)健性檢驗(yàn)。接下來我們分別介紹如何使用三種相對(duì)熵來確定最優(yōu)的風(fēng)險(xiǎn)中性測(cè)度。

模型1：最小KL相對(duì)熵方法

KL相對(duì)熵的定義為

(7)

其度量了風(fēng)險(xiǎn)中性測(cè)度Q關(guān)于真實(shí)測(cè)度P的差異程度，EP(·)表示在測(cè)度P下的期望算子。假設(shè)市場(chǎng)中有m種資產(chǎn)，存在N個(gè)概率路徑。當(dāng)概率路徑數(shù)等于市場(chǎng)中的資產(chǎn)數(shù)量，即N=m時(shí)，市場(chǎng)即被稱為完全市場(chǎng)， 此時(shí)存在唯一的風(fēng)險(xiǎn)中性測(cè)度；當(dāng)概率路徑數(shù)大于市場(chǎng)中的資產(chǎn)數(shù)量，即N>m時(shí)，市場(chǎng)即被稱為非完全市場(chǎng)，此時(shí)風(fēng)險(xiǎn)中性測(cè)度不唯一。通過最小化KL相對(duì)熵方法來求最優(yōu)風(fēng)險(xiǎn)中性測(cè)度即解決如下優(yōu)化問題：

(8)

Vi表示資產(chǎn)i的市場(chǎng)價(jià)格，fi(wj)表示在第j個(gè)概率路徑下第i種資產(chǎn)的價(jià)值。

設(shè)定拉格朗日函數(shù)形式為：

(9)

則一階條件為：

(10)

模型2：最小Tsallis相對(duì)熵方法

Tsallis相對(duì)熵的定義為

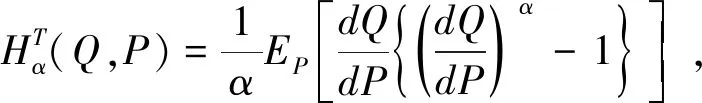
(11)

使用最小化Tsallis相對(duì)熵方法來求最優(yōu)風(fēng)險(xiǎn)中性測(cè)度即解決如下優(yōu)化問題

(12)

約束條件和模型1相同。拉格朗日函數(shù)為

(13)

一階條件為

(14)

模型3：最小Rényi 相對(duì)熵方法

Rényi 相對(duì)熵的定義為

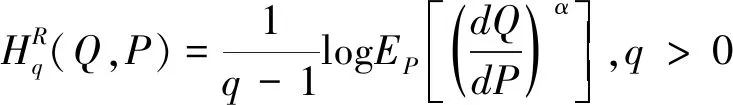
(15)

使用最小Rényi相對(duì)熵方法求最優(yōu)風(fēng)險(xiǎn)中性測(cè)度即解決如下優(yōu)化問題

(16)

在約束條件不變的情況下，拉格朗日函數(shù)變?yōu)?/p>

(17)

問題求解一階條件為

(18)

通過Matlab軟件進(jìn)行編程，使用數(shù)值解法在模型1-3中分別求得了最優(yōu)的風(fēng)險(xiǎn)中性測(cè)度Q后，依據(jù)公式

(19)

可以計(jì)算不同期限T下長(zhǎng)壽債券的風(fēng)險(xiǎn)市場(chǎng)價(jià)格，即可完成不同期限長(zhǎng)壽債券的市場(chǎng)定價(jià)。

5 實(shí)證模擬

(1)死亡率建模結(jié)果

本文采用了1986年-2016年的男女不同性別人口分年齡死亡率數(shù)據(jù)，1986年—2005年的死亡率數(shù)據(jù)來源為《中國(guó)人口統(tǒng)計(jì)年鑒》，2006-2016年的死亡率數(shù)據(jù)來源為《中國(guó)人口和就業(yè)統(tǒng)計(jì)年鑒》，其中1991-1993年對(duì)應(yīng)的年鑒中并未統(tǒng)計(jì)分年齡死亡率統(tǒng)計(jì)數(shù)據(jù)，故按年份采取平均插值法補(bǔ)齊這三年數(shù)據(jù)。由于早期死亡率數(shù)據(jù)統(tǒng)計(jì)僅統(tǒng)計(jì)到84歲，故我們選擇60-84歲的人群死亡率數(shù)據(jù)作為來估計(jì)CBD兩因子模型的參數(shù)，這一方面是由于長(zhǎng)壽債券主要針對(duì)高齡人群管理長(zhǎng)壽風(fēng)險(xiǎn)，選擇高齡人口建模得到的結(jié)果更準(zhǔn)確，對(duì)未來死亡率的模擬也更可信,另一方面Cairns等[28]還指出CBD模型對(duì)高齡人口死亡率的擬合效果更好，在該論文中他們也選擇60歲以上人群的死亡率數(shù)據(jù)來估計(jì)模型的參數(shù)。

圖1 1986年-2016年死亡率因子A1(t)的趨勢(shì)

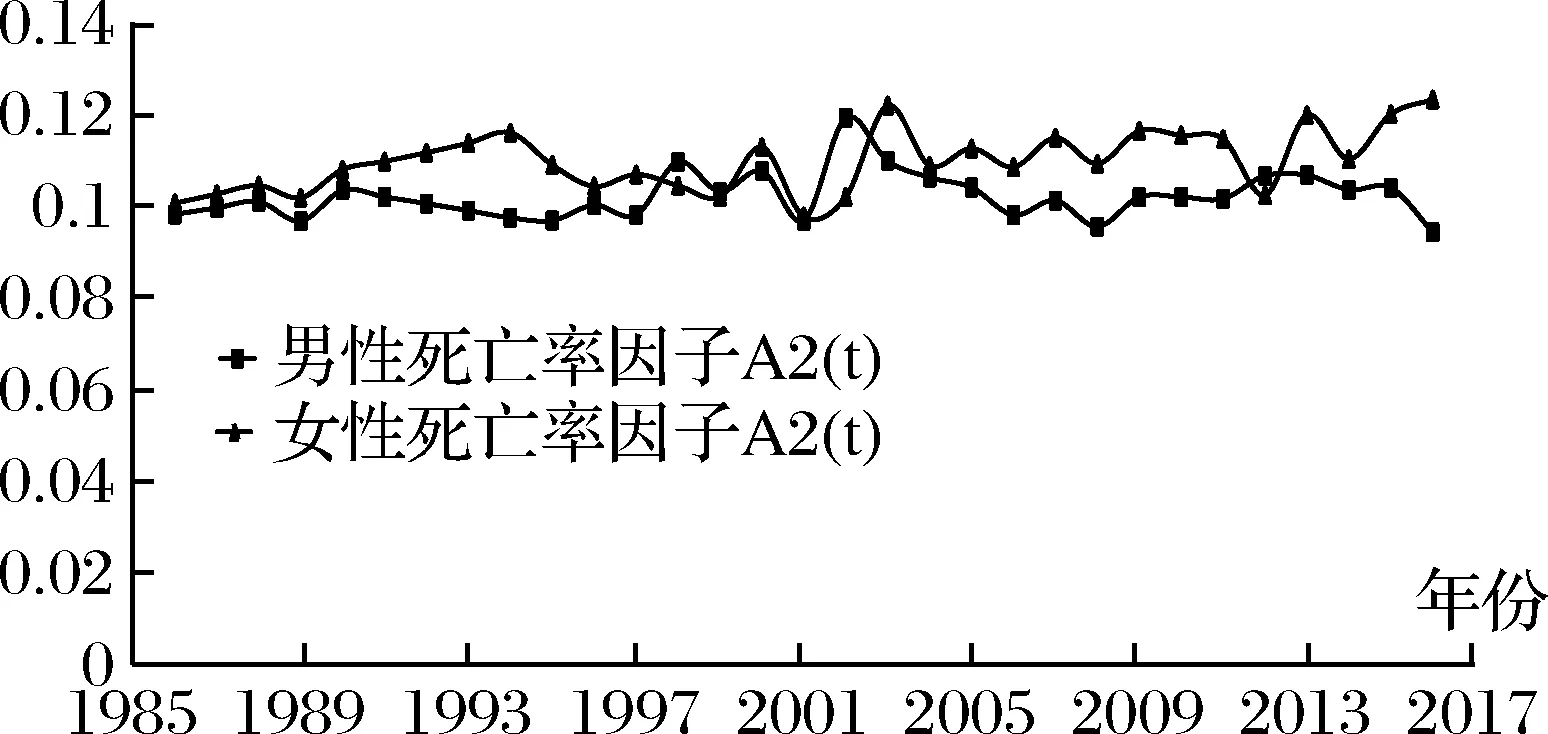
圖2 1986年-2016年死亡率因子A2(t)的趨勢(shì)

我們根據(jù)第3部分所列公式計(jì)算不同性別高齡人群的死亡率因子A1(t)和A2(t)以及CBD模型的相關(guān)參數(shù)。我們分別將A1(t)和A2(t)展示在圖1和圖2中。從圖中可以看出，對(duì)于男性人口的死亡率因子，無論因子A1(t)還是A2(t)均呈現(xiàn)緩慢下降趨勢(shì)，對(duì)于女性人口的死亡率因子，雖然A1(t)呈現(xiàn)更明顯的下降趨勢(shì)，但A2(t)反而呈現(xiàn)略微上升的趨勢(shì)。男性死亡率模型的相關(guān)參數(shù)估計(jì)結(jié)果為：

而女性死亡率模型的相關(guān)參數(shù)估計(jì)結(jié)果為

(2)風(fēng)險(xiǎn)價(jià)格信息

風(fēng)險(xiǎn)中性測(cè)度方法依賴于現(xiàn)有市場(chǎng)的完全性，現(xiàn)有市場(chǎng)的交易資產(chǎn)越多，能夠提供的關(guān)于風(fēng)險(xiǎn)的市場(chǎng)價(jià)格的信息越豐富，長(zhǎng)壽債券的定價(jià)也會(huì)越合理。為此我們需要搜集我國(guó)市場(chǎng)上相關(guān)金融資產(chǎn)的信息。從發(fā)行主體來看，長(zhǎng)壽債券和金融債類型最為接近。金融債是金融機(jī)構(gòu)所發(fā)行的債券，資信水平往往較高，該類債券的收益率相比無風(fēng)險(xiǎn)利率略高。我們從Resset金融數(shù)據(jù)庫中搜集了1998年-2018年發(fā)行的1650只金融債的期限和利率的數(shù)據(jù)，同時(shí)Resset數(shù)據(jù)庫還提供了1998-2018年的參考無風(fēng)險(xiǎn)利率。Resset數(shù)據(jù)庫的參考無風(fēng)險(xiǎn)利率數(shù)據(jù)在2002年8月6日之前是三個(gè)月銀行定存利率；2002年8月7日-2006年10月7日是三個(gè)月期央行票據(jù)利率，2006年10月8日之后的無風(fēng)險(xiǎn)利率是上海銀行間3個(gè)月同業(yè)拆借利率，此處使用參考無風(fēng)險(xiǎn)利率僅用于推算金融債的風(fēng)險(xiǎn)溢價(jià)，而在進(jìn)行長(zhǎng)壽債券定價(jià)所涉及到的無風(fēng)險(xiǎn)利率均如前文設(shè)定按常數(shù)4%計(jì)。根據(jù)債券的收益率以及無風(fēng)險(xiǎn)利率信息分別推算出了不同期限下的平均風(fēng)險(xiǎn)溢價(jià)，同時(shí)刪去少數(shù)異常的樣本(如債券期限非整數(shù)年以及風(fēng)險(xiǎn)溢價(jià)為負(fù)數(shù)等)；由于EIB/BNP債券的期限是25年，我們也剔除了期限超過25年的超長(zhǎng)期限債券，防止期限過長(zhǎng)影響計(jì)算結(jié)果的準(zhǔn)確性。我們將最終獲得的6種不同期限金融債的平均風(fēng)險(xiǎn)溢價(jià)信息展示在表1中，并將這6種“期限-溢價(jià)”的組合分別以A-F表示。A-F這幾種“期限-溢價(jià)”組合即代表了當(dāng)前市場(chǎng)所能提供的6種風(fēng)險(xiǎn)的市場(chǎng)價(jià)格信息。

(3)只考慮單個(gè)風(fēng)險(xiǎn)價(jià)格

假設(shè)僅包含單個(gè)風(fēng)險(xiǎn)市場(chǎng)價(jià)格信息，即僅有一種資產(chǎn)(m=1)，且以組合E的形式出現(xiàn),根據(jù)該組合的期限(10年)和風(fēng)險(xiǎn)溢價(jià)(δ=0.0069)代入到式(2)中計(jì)算出該資產(chǎn)的價(jià)格，并代入模型1- 3的約束條件中，即可分別計(jì)算出最優(yōu)風(fēng)險(xiǎn)中性測(cè)度Q，然后根據(jù)式(19)計(jì)算反推出不同期限的長(zhǎng)壽債券的溢價(jià)信息。我們將結(jié)果展示在圖3-圖5。

表1 金融市場(chǎng)不同“期限-溢價(jià)”組合

圖3 KL相對(duì)熵計(jì)算的風(fēng)險(xiǎn)溢價(jià)(m=1)

首先可以看出，在僅由一種資產(chǎn)提供市場(chǎng)信息時(shí)，男女人群長(zhǎng)壽風(fēng)險(xiǎn)溢價(jià)的整體趨勢(shì)差異不大，當(dāng)債券期限逐漸大于資產(chǎn)E的期限時(shí)，男女人群長(zhǎng)壽風(fēng)險(xiǎn)的市場(chǎng)價(jià)格基本趨同。這種趨勢(shì)在使用三種相對(duì)熵方法時(shí)表現(xiàn)一致；此外在使用Tsallis相對(duì)熵和Rényi相對(duì)熵時(shí)，我們還分別設(shè)置了不同模型參數(shù)α和q，但對(duì)最終結(jié)果影響很小。這表明了僅包含單個(gè)資產(chǎn)信息時(shí)，使用相對(duì)熵方法以及對(duì)不同性別人群的長(zhǎng)壽風(fēng)險(xiǎn)進(jìn)行定價(jià)，較難得到的有差異的風(fēng)險(xiǎn)市場(chǎng)價(jià)格信息。

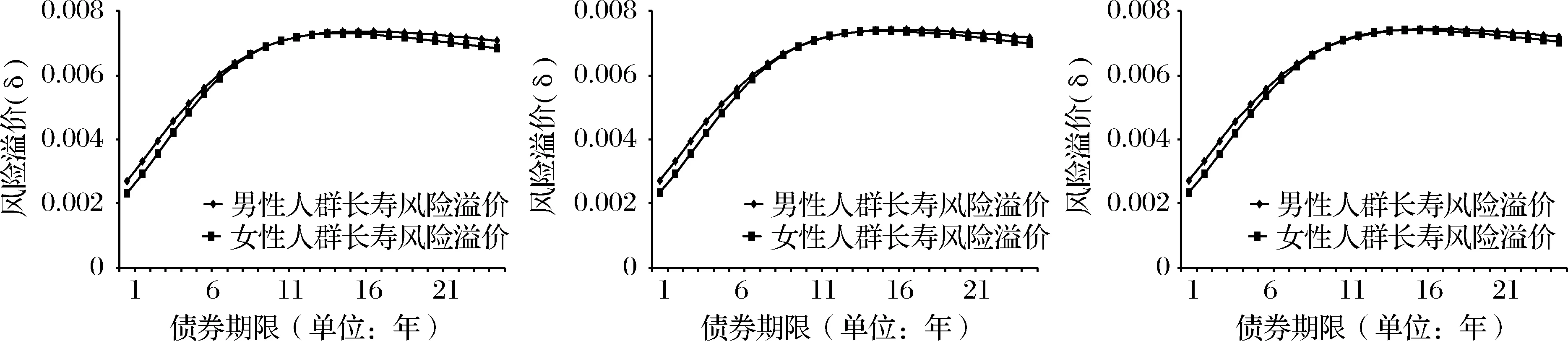
圖4 Tsallis相對(duì)熵得到的風(fēng)險(xiǎn)溢價(jià) (m=1)

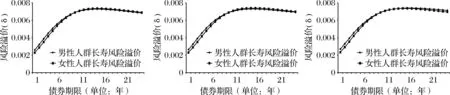
圖5 Rényi相對(duì)熵得到的風(fēng)險(xiǎn)溢價(jià) (m=1)

(4)考慮多個(gè)風(fēng)險(xiǎn)價(jià)格

接下來假設(shè)市場(chǎng)包含多個(gè)風(fēng)險(xiǎn)市場(chǎng)價(jià)格的信息，不妨假設(shè)要運(yùn)用A-F這6種“期限-溢價(jià)”組合來為債券正確定價(jià)提供信息，即在模型1-3中，m=6。分別根據(jù)式(2)求出這6種資產(chǎn)的價(jià)值，并代入模型1-3的約束條件來求解模型，然后將所得到的結(jié)果呈現(xiàn)在圖6-圖8中。

圖6 KL相對(duì)熵計(jì)算的風(fēng)險(xiǎn)溢價(jià)(m=6)

從圖6中可以看出，融合多個(gè)風(fēng)險(xiǎn)溢價(jià)信息的情況下，無論從不同性別角度，還是從不同期限角度去分析，長(zhǎng)壽債券所顯示的風(fēng)險(xiǎn)溢價(jià)都已有了顯著變化。無論是以男性人群還是以女性人群的生存指數(shù)為定價(jià)標(biāo)的，風(fēng)險(xiǎn)溢價(jià)與債券期限的關(guān)系均呈N型，即風(fēng)險(xiǎn)溢價(jià)在較短期限范圍內(nèi)會(huì)呈現(xiàn)極大值和極小值，與僅包含單一資產(chǎn)信息情形差別較大。這也是由于新加入的資產(chǎn)信息的約束造成的。從不同性別來看，男性和女性長(zhǎng)壽風(fēng)險(xiǎn)的市場(chǎng)價(jià)格信息是有差別的，女性長(zhǎng)壽風(fēng)險(xiǎn)的市場(chǎng)價(jià)格要略高于男性，這種表現(xiàn)尤其在期限較長(zhǎng)的債券中更為明顯。這表明，女性長(zhǎng)壽風(fēng)險(xiǎn)面臨的不確定性更明顯，因而市場(chǎng)會(huì)要求更多的風(fēng)險(xiǎn)溢價(jià)，特別是當(dāng)債券的發(fā)行期限逐漸增長(zhǎng)時(shí)，女性長(zhǎng)壽風(fēng)險(xiǎn)溢價(jià)與男性長(zhǎng)壽風(fēng)險(xiǎn)溢價(jià)的差距更明顯。

在圖7和圖8所展示的分別使用Tsallis相對(duì)熵和Rényi相對(duì)熵定價(jià)的結(jié)果來看，基本上也體現(xiàn)了相似的性質(zhì)。所不同之處表現(xiàn)在，使用Tsallis相對(duì)熵和Rényi相對(duì)熵進(jìn)行定價(jià)，不同性別的風(fēng)險(xiǎn)溢價(jià)體現(xiàn)的差異更加明顯，而當(dāng)α和q的大小趨近于1的時(shí)候，Tsallis相對(duì)熵和Rényi相對(duì)熵的定價(jià)表現(xiàn)又接近于KL相對(duì)熵，證明了定價(jià)結(jié)論的穩(wěn)定性。

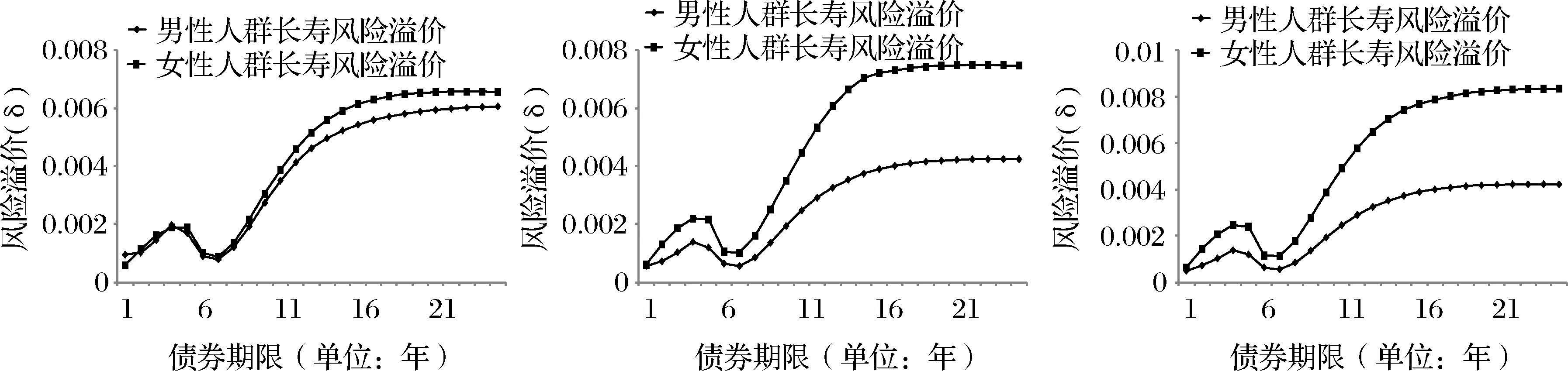
圖7 Tsallis相對(duì)熵得到的風(fēng)險(xiǎn)溢價(jià)(m=6)

圖8 Rényi相對(duì)熵得到的風(fēng)險(xiǎn)溢價(jià)(m=6)

同時(shí)，通過比較只考慮單個(gè)風(fēng)險(xiǎn)市場(chǎng)價(jià)格信息和考慮多個(gè)風(fēng)險(xiǎn)市場(chǎng)價(jià)格信息的情形，我們也發(fā)現(xiàn)，使用相對(duì)熵方法進(jìn)行定價(jià)，其結(jié)果對(duì)于市場(chǎng)中所能提供的證券數(shù)目較為敏感，體現(xiàn)在m=1和m=6兩種情形下，債券風(fēng)險(xiǎn)溢價(jià)隨期限變化而差別巨大。這主要是由于隨著資產(chǎn)數(shù)目的增加，也為整個(gè)市場(chǎng)提供了更為豐富的信息，而新信息的加入又必然會(huì)影響到風(fēng)險(xiǎn)中性測(cè)度的選擇，從而最終影響到債券風(fēng)險(xiǎn)溢價(jià)的表現(xiàn)。這也體現(xiàn)了相對(duì)熵方法的可塑性，即隨著市場(chǎng)完全度的提高，市場(chǎng)能夠提供的風(fēng)險(xiǎn)價(jià)格信息越豐富，債券的定價(jià)也將越來越合理。由此可見，增強(qiáng)長(zhǎng)壽風(fēng)險(xiǎn)管理能力，并不等價(jià)于一味地改進(jìn)定價(jià)技術(shù)和模型，一個(gè)健全穩(wěn)定的金融市場(chǎng)反而更能從根本上為長(zhǎng)壽風(fēng)險(xiǎn)管理提供巨大的支持。

6 結(jié)語

本文在使用CBD模型對(duì)我國(guó)男女人群死亡率進(jìn)行模擬的基礎(chǔ)上，結(jié)合相對(duì)熵方法，對(duì)我國(guó)EIB/BNP型長(zhǎng)壽債券進(jìn)行了定價(jià)。定價(jià)的過程中，本文盡可能地搜集了金融市場(chǎng)的風(fēng)險(xiǎn)市場(chǎng)價(jià)格信息，使定價(jià)結(jié)果能夠更貼近我國(guó)的實(shí)際情況；在定價(jià)方法上，選擇不同的相對(duì)熵進(jìn)行比較研究也保證了結(jié)論的穩(wěn)健性。同時(shí)本文以性別人群為研究對(duì)象進(jìn)行了定價(jià)，結(jié)果發(fā)現(xiàn)女性的長(zhǎng)壽風(fēng)險(xiǎn)不確定性更高。本文的研究也證明了應(yīng)該如何使用長(zhǎng)壽債券進(jìn)行長(zhǎng)壽風(fēng)險(xiǎn)管理。在擁有了高齡人口人年齡的歷史死亡率數(shù)據(jù)的觀測(cè)值之后，運(yùn)用本文所展示的方法，可以解決長(zhǎng)壽衍生品的定價(jià)難題。但本文的研究模型也依賴于對(duì)現(xiàn)有金融市場(chǎng)信息的獲取，準(zhǔn)確而豐富的市場(chǎng)信息獲取將使得定價(jià)更為合理。因此，對(duì)于長(zhǎng)壽風(fēng)險(xiǎn)的管理，除了要在技術(shù)和產(chǎn)品上進(jìn)行創(chuàng)新之外，還需要促進(jìn)金融市場(chǎng)健康持續(xù)的發(fā)展，發(fā)達(dá)的金融市場(chǎng)將提供更豐富的產(chǎn)品信息，為長(zhǎng)壽風(fēng)險(xiǎn)的管理提供有力的支撐。