帶預算約束的廣告主均衡報價研究
——基于納什均衡角度
韓 帥,劉樹林
(1.山西財經大學國際貿易學院,山西 太原 030006;2.對外經濟貿易大學國際經濟貿易學院,北京 100029)
1 引言
隨著全球信息產業的高速成長,截至2017年6月,我國互聯網用戶規模已達到7.51億,穩居世界第一,2017年上半年新增用戶數量1992萬,互聯網普及率達到54.3%,比2016年底提升1.1%,預計2017年底我國互聯網用戶數量將達到7.72億,互聯網普及率將到達55.9%。在這個信息爆炸的時代,廣大網民對于所獲信息的準確度需求也在逐步提高。黨的十九大報告指出,我國社會的主要矛盾已經轉化為人民日益增長的美好生活需求和不平衡不充分的發展之間的矛盾。傳統的信息獲取方式已很難滿足人們的需求,網絡搜索的重要性也愈發顯著。關鍵詞廣告作為搜索引擎向網民投放廣告的一種途徑,已成為互聯網企業重要的盈利模式之一。大量的廣告主把部分廣告費用投資到搜索引擎,以便在更大范圍內宣傳和銷售自己的產品及服務。在美國當地時間2017年10月27日,國際知名搜索引擎Google的母公司Alphabet發布了截至2017年9月30日的第三季度財報。內容顯示,Alphabet今年第三季度總營收為277.72億美元,同比增長24%,凈利潤為67.32億美元,較去年同期的50.61億美元,同比增長28%。而該公司的主要收入來源為在線廣告營銷服務,實際情況也表明互聯網廣告對于互聯網企業獲取利潤的重要影響不言而喻。關鍵詞廣告是在線廣告的重要組成部分,而關鍵詞拍賣作為關鍵詞廣告的出售模式,有必要對其進行理論研究。
關鍵詞拍賣的早期研究多集中在拍賣機制設計及改進方面,并沒有考慮廣告主有預算約束的情況。Varian[1]最先將博弈論引入關鍵詞拍賣領域,給出關鍵詞拍賣模型的納什均衡(Nash Equil-ibrium, NE)和對稱納什均衡(Symmetric Nash E-quilibrium, SNE)的定義及相關性質,還指出搜索引擎在廣義第二價格(Generalized Second Price, GSP)拍賣機制下的收益不低于在Vickrey-Clarke-Groves(VCG)機制下的收益。而Edelman等[2]進一步研究了GSP機制,證明說真話(報價等于估價)不是GSP機制的占優策略,并給出局部無嫉妒均衡(Locally Envy-Free Nash Equilibrium, LEFNE)的概念,證明局部無嫉妒均衡與SNE是等價的。這兩篇論文是最早研究關鍵詞拍賣的文獻,屬于本領域的奠基性工作。在此基礎上,Bu Tianming等[3]認為廣告主可以同時提交多個報價,分析了該情形下滿足純策略納什均衡的條件。Fukuda等[4]借鑒Edelman的方法,使用LEFNE研究VCG機制,并給出該機制下廣告主均衡報價的區間。為了獲取最大社會福利,Yuan Yong等[5]研究了廣告主的合作式穩定型報價策略,應用進化博弈理論與合作進化模擬于重復關鍵詞廣告拍賣,發現“友好”報復策略可以促使競爭廣告主間形成穩定的合作機制。Thompson和Leyton-Brown[6]針對主流搜索引擎大多采用加權GSP機制銷售關鍵詞廣告位的現象,提出一種“計算機理分析”的方法,計算該模型的納什均衡,并與其他三種位置拍賣模型及七種已有估計模型進行對比,發現wGSP在社會福利和預期點擊數兩方面的表現都是最好的。原全和汪定偉[7]基于廣義第一價格拍賣,建立關鍵詞拍賣的最優投標價格決策模型,并由此給出廣告主獲取最大期望收益時的報價。針對關鍵詞拍賣中虛假廣告泛濫問題,殷紅[8]在GSP機制中引入廣告主信譽度,建立可信競價排名機制。當廣告主信譽度差別很大時,改進機制在搜索引擎收益和拍賣效率方面的優勢顯著。用戶興趣度對點擊率也有較大影響,董紅斌等[9]在GSP機制中引入興趣度因子,建立基于興趣度的拍賣模型,對于點擊數、搜索引擎收益的范圍以及拍賣配置效率均有小幅提高,但損失了部分運行效率,等價于用時間換取收益。
隨著該領域研究不斷深入,部分學者開始關注廣告主預算對關鍵詞拍賣的影響。Abrams等[10]使用線性規劃的方式,研究了考慮預算的廣告主最優收益問題。Chen Ligang和Li Yijun[11]對于廣告主選擇不同搜索引擎及如何進行預算分配的問題進行分析,指出應依照不同目標對預算進行合理分配。Hafalir等[12]提出一種Sort-Cut拍賣機制,研究了特征相同關鍵詞的多輪拍賣問題,廣告主不能通過低報預算或保守估價獲益,但是高估預算和估價可以提高收益。Muthukrishnan等[13]從概率角度建立預算優化模型,并通過該模型預測網民檢索行為數據的概率分布狀況。Gummadi等[14]應用馬爾科夫決策法分析帶預算廣告主的競價問題。Cholette等[15]采用概率方法,找到廣告主支付不超過預算的最優報價。Koh[16]基于SNE,建立考慮廣告主預算約束的關鍵詞拍賣模型,給出并證明了廣告主提高報價后無利可圖的充要條件,通過實例說明降低報價后收益變化是不確定的,由此得出報價向量是帶預算約束的SNE條件,最后分析了在一個理想環境下,搜索引擎的收益情況以及兩位廣告主組成的報價向量是非占優策略均衡的條件。Zhang Jie等[17]研究了廣告主報價和每日預算的動態調整,避免預算浪費在早期無效點擊上,以獲取更好的廣告投放機會。Arnon和Mansour[18]將重復性付費搜索廣告拍賣看作單次博弈行為,并稱為預算拍賣,其中每位廣告主需要提交一個報價和預算,使用序貫第二價格拍賣機制出售廣告位,發現當廣告主報價不高于估價,該博弈存在純策略納什均衡。楊彥武等[19]從跨搜索引擎與時間序列的角度,研究關鍵詞拍賣中的預算分配與調整問題,構建出能夠提高分配效率的策略模型。于洪雷等[20]將廣告主按估價和預算分布進行分類,分別從長期與短期角度建立模型,研究預算約束下GSP機制的均衡投標策略問題,得到靜態與動態環境下關鍵詞拍賣的均衡點。楊雪等[21]基于預算約束限制,首次構建形式化的視頻廣告拍賣模型,與關鍵詞拍賣類似,該模型不限制參與競拍者的邊際效用形式。通過對比三種線性收益函數和一種非線性收益函數,證明改進機制收益和社會效用的有效性,并分析不同預算約束對機制的影響。與國外發展情況相比,國內研究帶預算約束的關鍵詞拍賣文獻較少,還處于起步階段。
綜上所述,已有的關鍵詞拍賣研究存在以下不足:首先,許多研究未考慮廣告主的預算約束,但在實際情況中,即使是市值很高的大企業,它的廣告預算也是有限的,廣告主需要事先制定關鍵詞廣告的投標策略。因此有必要從理論上對該問題進行深入分析。其次,由于SNE條件的一致性,現有研究帶預算約束問題的文獻,主要采用該均衡條件。當今主流搜索引擎均使用GSP機制,但是GSP的缺陷在于任意廣告主維持在原位不向上偏離的不等式不符合GSP機制,相較下NE條件符合該機制[22]。最后,2017年底召開的中央經濟工作會議中已提出,我國經濟發展進入新時代,基本特征是我國經濟已由高速增長階段轉向高質量發展階段。而高質量的發展就需要企業提高經營效率,合理使用預算資金,從而達到效用最優。因此,利用NE概念研究如何合理地利用預算更具有應用價值。
鑒于此,本文受Koh[16]的啟發,使用NE概念研究預算約束下廣告主的均衡報價問題,分別從報價向上偏離和向下偏離兩方面進行分析,給出了廣告主報價達到均衡時所應滿足的充要條件。這將有助于廣告主進行預算的合理分配,給出最優報價,從而獲得最大收益。本文與之前研究的主要區別在于:第一,本研究基于NE分析帶預算約束的廣告主達到均衡報價的條件,相比SNE更符合實際情況。第二,本研究根據NE條件推導出滿足NE的廣告主報價的上下界,并與SNE的上下界進行了對比。第三,本研究給出了報價向量達到帶預算約束的納什均衡時應滿足的條件。相比不考慮預算約束的情況,帶預算約束的情況要復雜的多,需要從報價偏離的角度得出結論,并闡述了此均衡條件的實際意義。
2 模型建立
2.1 基本模型
假設模型中有n位廣告主競爭獲得s個廣告位,其中n≥s,由廣告主構成的集合為N={1,2,…,n},而廣告位組成的集合為S={1,2,…,s}。該模型的保留價為0。廣告主j的估價、報價、支付與收益分別為vj,bj,pj與πj,其中j∈N。cj表示在單位時間內廣告位j獲得的點擊數,其中j∈S。由網民瀏覽習慣可知,不同廣告位對網民的吸引力由上到下嚴格遞減[22],有c1>c2>…>cs,而且僅有s個廣告位,故cs+1=cs+2=…=cn=0。
下面對每位廣告主重新進行編號,以便于后續表述。獲得廣告位j的廣告主的報價記為bj,估價為vj。本研究中廣告主支付使用GSP機制,且該模型是完全信息的,即所有cj,bj,vj都是已知的。因此,廣告主j的支付滿足pj=bj+1,收益為πj=cj(vj-bj+1)。
下面回顧Varian構建關鍵詞拍賣的兩種不同均衡[1]。
定義1 若所有參與競拍的廣告主的報價構成的向量b=(b1,b2,...,bn)滿足以下條件:
cj(vj-bj+1)≥cl(vj-bl+1),?l>j
(1)
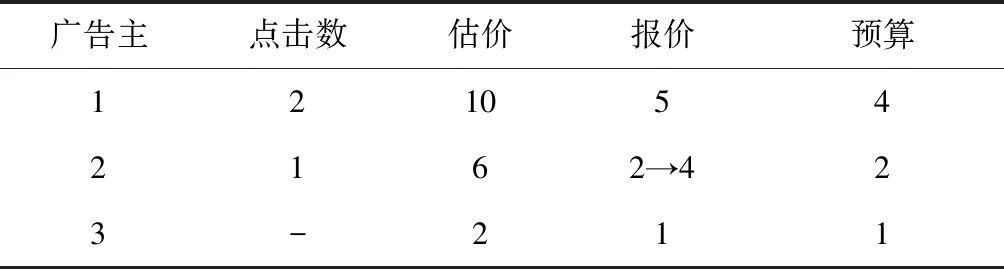
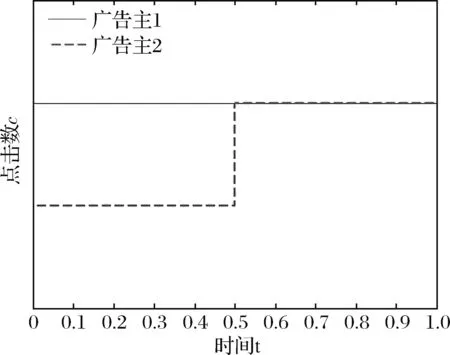
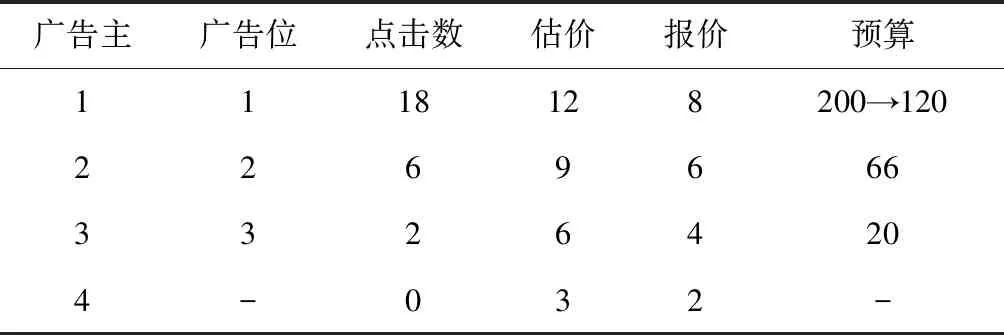
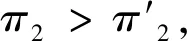
cj(vj-bj+1)≥cl(vj-bl),?l (2) 則稱報價向量b是NE。 定義2 若所有參與競拍的廣告主的報價構成的向量b=(b1,b2,…,bn)滿足以下條件: cj(vj-bj+1)≥cl(vj-bl+1),?l,j (3) 則稱報價向量b是SNE。 通常滿足NE的報價向量很多,故采用BNE表示報價向量是NE的集合。同理,采用BSNE表示報價向量是SNE的集合。兩個集合均未考慮廣告主的預算。從定義可以看出,NE與SNE的主要區別是任意廣告主j報價不向上偏離的條件。 為了簡便,令競拍全程時間為1,例如實際中的1天。假設廣告主j為理性人,顯然他的報價不會超過估價,從而有vj>pj=bj+1。 定義3 假設廣告主j的報價為bj,獲得廣告位θ(j),支付為pj,其預算給定為Bj,參與競拍的時間為tj,其中j∈N。若報價向量b=(b1,b2,…,bn)滿足: (1)b∈BNE; (2)如果廣告主j的支付pj≤Bj,則其參與競拍的時間tj=1,即全程占據廣告位θ(j),其中j∈N; (3)如果廣告主j的支付pj>Bj,則其參與競拍的時間tj=Bj/pj<1,將提前退出競拍,其中j∈N; (4)對任意廣告主k(k≠j),bk都不改變。廣告主j的報價向上偏離占據靠前廣告位后收益沒有增加,向下偏離占據靠后廣告位后收益也沒有增加,其中k,j∈N。即模型中任意廣告主報價bj向上偏離后無利可圖,并且bj向下偏離后同樣無利可圖,則稱該向量b是帶預算約束的納什均衡(Nash Equilibrium with Budget Constraint, NE-B)。 下面用數例解釋引入預算后對拍賣模型的影響。 例1 考慮3位廣告主競拍2個廣告位的情況。詳細信息如下表。 表1 信息列表 圖1 帶預算廣告主所在廣告位點擊數受報價變化的影響 從圖1可以看出,廣告主2提高報價后,在時期[0,0.5],廣告主1占據首位,廣告主2位居次席;在時期[0.5,1],廣告主1提前退出,廣告主2占有廣告位1,廣告主3占據廣告位2。由于廣告主2的全程支付價格p2=0.5c2b3+0.5c1b3=1.5 該結果表明考慮預算約束會使廣告主產生改變自身報價的動機(收益增加)。 本文研究的是基于納什均衡的帶預算廣告主的均衡報價問題,而得到在此均衡下廣告主報價的取值邊界有助于分析報價向量達到NEB應滿足的條件。 首先將定義1中的兩個不等式分別進行化簡,則報價bj應滿足: (4) (5) (6) 根據式(4)可以得到滿足NE條件的報價向量中bj的上下界。 (7) 證明:由于報價向量b∈BNE,所以式(1)成立。令l=j+1,可得: cj(vj-bj+1)≥cj+1(vj-bj+2) 化簡得: bj+1≤(cj-cj+1)vj/cj+cj+1bj+2/cj 由此推導可以得到: bj≤(cj-1-cj)vj-1/cj-1+cjbj+1/cj-1≤(cj-1-cj)vj-1/cj-1+cj[(cj-cj+1)vj/cj+cj+1bj+2/cj]/cj-1 繼續遞推可得: bj≤(cj-1-cj)vj-1/cj-1+(cj-cj+1)vj/cj-1+…+(cs-1-cs)vs-1/cj-1+csbs+1/cj-1 (8) 令式(4)中j=s+1,并且cs+1=0,則廣告主s+1的報價滿足: (9) 將式(9)代入式(8)整理: 綜上,定理1得證。 (10) 證明:由于報價向量b∈BNE,故式(2)成立。令l=j-1,可得: cj(vj-bj+1)≥cj-1(vj-bj-1) 化簡得: bj-1≥(cj-1-cj)vj/cj-1+cjbj+1/cj-1 由此推導可以得到: bj≥(cj-cj+1)vj+1/cj+cj+1bj+2/cj≥(cj-cj+1)vj+1/cj+cj+1[(cj+2-cj+3)vj+3/cj+2+cj+3bj+4/cj+2]/cj>(cj-cj+1)vj+1/cj+cj+2[(cj+2-cj+3)vj+3/cj+2+cj+3bj+4/cj+2]/cj, (cj+1>cj+2>0) 繼續遞推下去。當s與j奇偶性相同時,報價bj滿足: bj≥(cj-cj+1)vj+1/cj+(cj+2-cj+3)vj+3/cj+…+(cs-2-cs-1)vs-1/cj+cs-1bs/cj (11) 令式(4)中的j=s,并且cs+1=0,則廣告主s的報價滿足: (12) 將式(12)代入式(11)整理得: bj≥(cj-cj+1)vj+1/cj+…+(cs-2-cs-1)vs-1/cj+cs-1vs+1/cj>(cj-cj+1)vj+1/cj+…+(cs-2-cs-1)vs-1/cj+csvs+1/cj, (cs-1>cs>0) 同理,當s與j奇偶性相異時,bj滿足: 綜上所述,定理2得證。 定理1與2給出了NE條件下報價的理論取值范圍,該結論為研究帶預算廣告主的均衡報價策略提供了理論基礎。 本節分析報價向量b∈BNE達到NEB時廣告主應具備的條件。研究將分別從不同方向的報價偏離著手,首先考察報價向上偏離的情形。 定理3任意報價向量b∈BNE,預算Bj對所有廣告主j∈N都滿足cjbj+1≤Bj,則任意報價bj(1 (1)當Bj≥cj-k+1bj-k+1,廣告主j將始終占據第j-k+1位,其收益為πj=cj-k+1(vj-bj-k+1)。 假設式(2)中l=j-k+1,得到cj(vj-bj+1)≥cj-k+1(vj-bj-k+1),所以此時廣告主j的報價向上偏離后無利可圖。 (2)當Bj 同理,令式(2)中l=j-k+1,有cj(vj-bj+1)≥cj-k+1(vj-bj-k+1)≥cj-k+1t(vj-bj-k+1)。這說明預算不足時,廣告主j的報價向上偏離也無利可圖。故定理3充分性證畢。 (必要性)假設報價向量b∈BNE,對所有j∈N有cjbj+1≤Bj。下面使用反證法。假設廣告主j的預算Bj 廣告主j+1在第j+1位的時間為t,而上升一位后占據第j位的時間為t′-t,其中t′滿足[cj+1t+cj(t′-t)]bj+2=Bj+1,可能大于1。由于采用GSP機制,廣告主j+1的支付需要分析廣告主j+2所處的位置。 (1)廣告主j+2占據第j+2位的時間為t,故廣告主j+1占據第j+1位的支付為cj+1bj+2; Δπj+1=[cj+1t+cj(min{t′,1}-t)](vj+1-bj+2)-cj+1(vj+1-bj+2) 所以廣告主j+1的報價向上偏離后收益增加,必要性得證。定理3證畢。 定理3揭示了當報價向量滿足NE條件時,任意一位廣告主提高報價無利可圖應滿足的充要條件。由定理3可以看出,廣告主j的預算至少需要達到cjbj,否則其向上偏離后將獲得的更大收益。由該定理將逐步分析出廣告主報價達到NEB時需要滿足的條件。 該推論運用定理3的結論,當廣告主預算較低時,后一位廣告主提高報價是有利可圖的,所以此時報價向量不滿足NEB條件。該結論說明當某位廣告主制定的廣告預算較少時,排名靠后的廣告主將有動機提高報價競爭該廣告位,以獲取更高收益。因此,廣告主們的預算分配過少將導致無法達到NEB。 下面從實例角度,驗證定理3的結論。 例2 構建一個拍賣模型,其中4位廣告主競爭3個廣告位。模型信息如表2所示,其中預算Bj≥cjbj,(j=1,2,3)。 表2 報價向量信息列表 (1)驗證該報價向量b∈BNE。 廣告主1在不同位置: c1(v1-b2)=108>c2(v1-b3)=48>c3(v1-b4)=20>c4(v1-b5)=0。 可知b1滿足NE條件。 同理,可以驗證b2,b3,b4均滿足NE條件,但不滿足SNE條件。因此,該報價向量b=(b1,b2,b3,b4)∈BNE。 (2)驗證定理3的充分條件。以廣告主2為例,由于預算滿足Bj≥cjbj,(j=1,2,3),則廣告主2報價向上偏離無利可圖。 廣告主2在第2位的收益: π2=c2(v2-b3)=6×(9-4)=30。 當b2向上偏離到第1位時,由于預算B2=66 即b2向上偏離后收益增加,定理3的必要條件成立。 對于廣告主報價向下偏離的收益變化情況,首先利用實例結果進行說明。 例3 同樣采用例2的相關數據。先計算NE下所有報價的邊界。 表3 報價向量信息列表(邊界) 先驗證該報價向量b∈BNE。廣告主1在不同位置: c1(v1-b2)=144>c2(v1-b3)=54>c3(v1-b4)=24>c4(v1-b5)=0。 可知b1滿足NE條件; 而廣告主2在不同位置: c2(v2-b3)=36>c1(v2-b1)=18=c3(v2-b4)=18>c4(v2-b5)=0, 而c1(v2-b2)=90>c2(v2-b3)=36。 可知b2滿足NE條件,但不滿足SNE條件。 同理可驗證b3,b4均滿足NE條件,但不滿足SNE條件。故該報價向量b=(b1,b2,b3,b4)∈BNE。 c1(v1-b2)=24≥c2(v1-b3)=24>c3(v1-b4)=12>c4(v1-b5)=0。 可知b1滿足NE條件。 同理可知b2,b3,b4均滿足NE條件,并且b4也滿足SNE條件。因此,該報價向量b=(b1,b2,b3,b4)∈BNE。 (4)情形(2)和(3)中b取值不同,將對b1向下偏離產生不同影響。 對于情形(2),初始時廣告主1的收益為π1= 因此,情形(2)中b1向下偏離無利可圖; 因此,情形(3)中b1向下偏離有利可圖。 以上兩種情形中,廣告主1的收益變化產生差異的原因有兩點:第一,b1降低至第2位,從而導致所占位置的點擊數減少(c2t+c1(1-t) 例如情形(2),由于廣告主2參與競拍時間(t=11/12)較長,盡管廣告主1在第2位時單次點擊收益增加,但點擊數的損失更大,故其收益下降;對于情形(3),廣告主1在第2位的時間(t=11/32)較短,在廣告主2退出后,他所在廣告位的點擊數恢復至第1位的水平,并且剩余競拍時間較長,致使其收益增加。 定理4若廣告主j(j∈N)的報價bj向下偏離,其收益將由所在廣告位點擊數與單次點擊收益共同決定。廣告主j的收益變化取決于兩者中占優因素的變化趨勢。 由例3的分析可以看出,廣告主報價bj向下偏離的情況比較復雜,在此情形下準確描述廣告主的收益變化較為困難。下面將從側面角度研究報價向量b達到NEB應滿足的條件。 由于cjt+(1-t)cj-1>cj,故上式中不等式成立。 該引理的結論與4.1節中推論類似,如果報價向量b中某位廣告主設置的廣告預算較低,則b將不滿足NEB。 ∈BSNE,即: (13) 廣告主j的初始收益可轉化為: 同理,由式(7)可得,廣告主j報價向上偏離一位(第j-1位)后的支付: 因此,式(13)對l=j-1,j+1均成立。引理2得證。 因此,報價向量b∈BNE是NEB。充分性成立。 綜上,定理5得證。 納什均衡是博弈論中最重要的理論之一,為現代經濟理論的發展奠定了堅實的基礎。早期關于關鍵詞拍賣的研究,為了便于分析,幾乎不考慮有預算約束的情況,而且多數沒有從納什均衡角度研究。但在實際情況中,廣告主在搜索引擎網站投放關鍵詞廣告必須考慮預算約束。因此,本文重點研究了帶預算約束的關鍵詞拍賣問題。主要結論可歸納為以下三個方面: (1)推導出基于NE的廣告主報價邊界,并與SNE條件下的報價的邊界進行對比,發現兩種均衡下的報價上界相同,而下界大小取決于排序j的大小。這是由于NE中不向下偏離條件與SNE相同,而不向上偏離條件不同所導致的。 (2)預算對于報價向量達到NEB具有顯著影響。廣告主只有具備充足的預算才能夠持續參與競拍,否則就要提前退出。此外,由于GSP機制的特點,若某位廣告主預算分配較少,排位較低的廣告主出于提高自身收益的目的,也會產生向上偏離的動機。通過研究發現,帶預算的廣告主向上偏離無利可圖除了需要滿足NE條件外,預算Bj也不能低于cjbj。而向下偏離的情況較為復雜,廣告主的收益變化取決于所在廣告位點擊數與單次點擊收益兩者占優因素的變化趨勢。 本文的主要創新在于:第一,基于NE條件,在關鍵詞拍賣中引入廣告主預算這一影響因素建立模型。通過對比Koh[16]研究SNE中帶預算約束的關鍵詞拍賣模型,發現其中不向上偏離的不等式右側廣告主的支付價符合第三價格拍賣機制(pj=bl+1,?l 鑒于帶預算約束的關鍵詞拍賣涉及的問題較多,本研究還存在著三個方面的不足。第一,實際中關鍵詞拍賣的情況更為復雜,很多參數和假設條件都不固定,例如廣告主的數量、廣告位數等,本文的假設與實際情況還存在一定差距,今后可以調整假設條件,使研究結果更符合實際。第二,本文結論的前提條件是完全信息博弈,而任意一位廣告主進行決策時,往往無法獲得其他外界的信息,未來可以通過概率分布的方式將研究拓展到不完全信息模型中。第三,受選題限制,本文僅從廣告主角度對帶預算約束的均衡報價問題進行研究,后續研究可以從搜索引擎的角度分析在帶預算約束的納什均衡下,預算約束對搜索引擎收益的影響,以及搜索引擎如何改進機制設計可以使社會效率提高等問題。2.2 改進模型
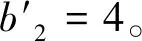
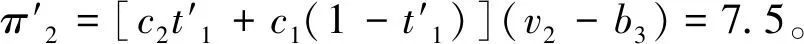
3 基于納什均衡的廣告主報價邊界


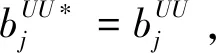
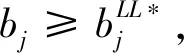
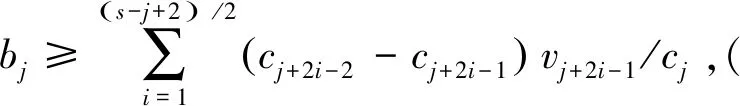
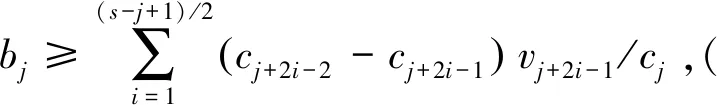
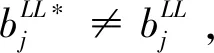
4 帶預算約束的納什均衡
4.1 報價向上偏離
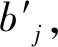
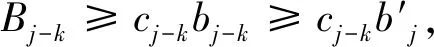
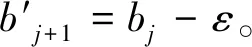

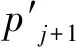
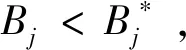
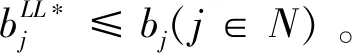
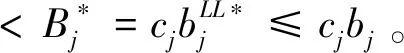

4.2 報價向下偏離
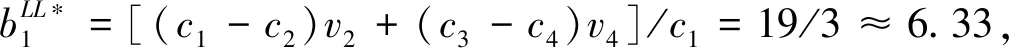
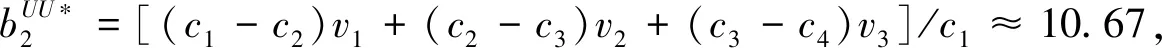
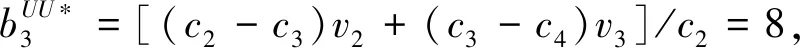
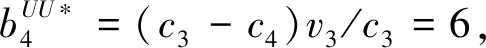
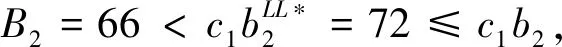

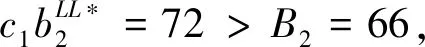

4.3 均衡條件
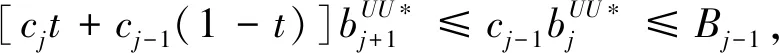
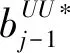
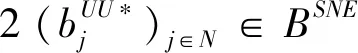
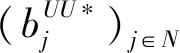
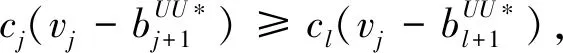
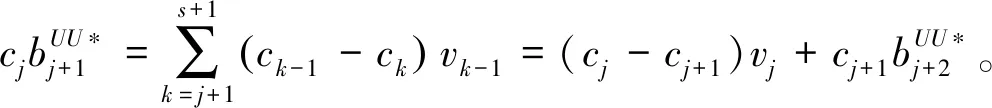
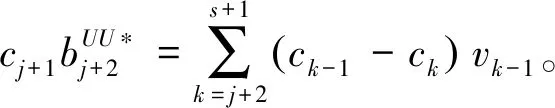
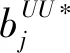
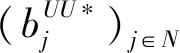
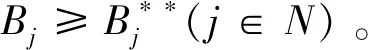
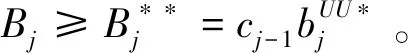
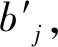
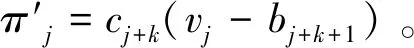
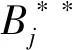
5 結語