“退”“推”之間“玩”出智慧*
——六年級《玩數學棋》一課的教學與思考

【設計理念】

1.“玩”中碰壁，問題讓智慧生根。

在現實教學中，數學教師雖然都致力于兒童思維能力的培養，可有時收效甚微。究其原因，兒童常常因為面對的問題是“偽問題”而興致不高，內驅力大打折扣，致使其缺乏主動思考的意識與能力。那么，怎樣尋找“真問題”？怎樣讓兒童的內心長出“真問題”呢？只有讓兒童有真實的在場感，他們才能真正把面臨的問題視作自己的問題，才能有積極的心向，主動尋找解決問題的策略。康德說：“教育即自由。”自由既是兒童的天性，也是需要我們為他們創造的條件。“愛玩”是兒童的天性。那么，怎樣讓兒童以“玩”的精神參與數學學習，讓兒童自由地“玩”，創造性地“玩”，玩出智慧呢？在教學中，為兒童創造值得“玩”的場域很重要，因為兒童在能玩而又不能駕馭的矛盾中，各種問題就自然產生了，智慧就有了“抓地力”。

2.“玩”中探索，困難驅智慧生長。

問題越明晰，解決時的方向就越明確。面對各種問題，怎樣通過比對、抽象讓兒童直面本質問題，并梳理出主線問題呢？于是，“接下來怎么思考呢？”就成了直接驅動兒童思考的主線索。教學中，教師往往更在意怎么幫學生解決眼下的問題，而深陷于尋找具體的步驟、方法或策略。事實上，“你是怎么想到的？”才是最重要、最值得思考的問題。所以，教學中更需要讓學生始終抱有客觀審慎的態度，學會反向思考——“我之所以不能前進，困難在哪里？”，退到自己能確定、能解決的問題處，然后不斷擴大思考范圍，挖掘思考深度，從而解決問題。

3.“玩”后自省，方法助智慧生成。

獲得問題解決的喜悅是教學追求的目標之一，但不是終極目標，沉淀下經驗、方法才可能生成智慧。所以，在教學中，要讓學生有靜下來再思考和慢下來再玩味的機會。如此，才能促進他們完善認知結構，提升應對未來的能力。

【教學目標】

1.通過玩數學棋積累數學活動經驗，體驗研究問題的策略，并在此過程中著力培養推理能力。

2.在交流分享中學會辯證地傾聽，并有理有據地表達自己的推理過程。

3.在活動中進一步感受數學的親切感與趣味性。

【課堂實錄】

一、談話：引出玩棋游戲

師：同學們，今天我們一起來玩（板書：玩）。說一說，你會玩些什么？

生：會玩游戲、圍棋、撲克、籃球、圍棋……

師：同學們會玩的東西真多！如果你就只是玩玩，很容易就沒興趣了；如果邊玩邊思考，你就會玩出水平，甚至還能玩出智慧。今天，我們就一起來玩數學棋（板書：數學棋），看看能否玩出新的體會。

二、比賽：思考玩棋中的問題

1.比賽，好奇中引發問題。

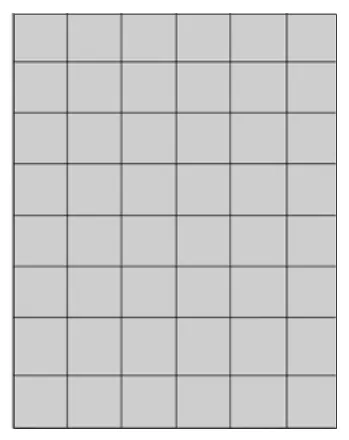
（圖1）

（1）教師講解游戲規則：瞧！這就是棋盤（如圖1），左下角有一個紅旗（放上紅旗磁塊），表示終點。在棋盤右上角有一枚棋子（放好黑色磁塊），兩人輪流移動這枚棋子，每人每次只能向左、下或左下移動一格（板書：），誰先移入紅旗格誰就獲勝。

（2）指名一男一女兩個學生玩

師：你倆誰先走？

男生：女生優先。

師：真有風度！其余同學注意觀察，看他們是否符合規則。好，開始！

很快，比賽結束，男生輸了。

師：我宣布，這一輪，女生獲勝。（舉起女生的手，然后采訪男生）剛才你輸了，想不想再玩一次？（男生歡喜地點頭）

師：大家猜猜他這時在思考什么問題？

生1：先走，還是后走？

生2：朝哪個方向走呢？

師：同學們說的其實是同一個問題——怎樣才能贏呢？那么，有沒有必勝的策略呢？

2.嘗試，初步探明研究方向。

（1）同桌嘗試玩2次，思考初步的方案

師：同桌的桌上有這樣的材料袋，先將笑臉磁塊放到終點格，再找到起點格。同桌共玩2次。邊玩邊思考：怎樣才能必勝呢？

同桌玩，教師巡視，收集學生的想法。

（2）談話，讓學生明確研究方向

師：剛才，同學們玩得很高興，你們找到必勝的對策了嗎？（少數人舉手）

生1：我覺得后走的肯定贏，我兩次都后走的，兩次都贏了。

生2：反對，我也后走的，沒有贏。

生3：我先走的時候也贏過。

師：呀，看來這個問題挺復雜。想一想，它究竟復雜在哪里？

生1：方向很多，情況很多，很復雜。

生2：而且你不能控制對方，指定他怎么走，所以有很多不確定因素，太復雜了。

生3：棋盤這么大，步數又多，很復雜。

師：面對這么復雜的問題，應該從哪里開始研究呢？（學生思考，但無所得）

師：你們真是下到最后一步才知道輸贏的嗎？

生1：我們到“田字格”里就知道了。

生2：我們到“九宮格”就知道了。

師：那我們就從最簡單的、能確定的那一步開始研究，好嗎？

師（出示2×2情況）：剛剛有人說到這種情況就可以確定了，誰能解釋解釋？

生：誰先到這三個虛線圈格中的任意一格（如圖2），對方都可以直接進入紅旗格，所以這三格是必輸格。

（圖2）

師：我們給這三個必輸格做個記號“×”（如圖 3）。哎，我們要找必勝的方法，卻找到了必輸點，這對我們找必勝的方法有用嗎？

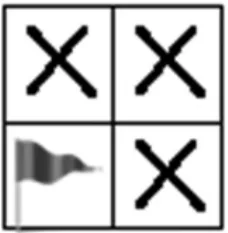
（圖3）

生：有用。可以借助它往外推。

師：那么，接下來，我們該怎么研究？

生：我們可以把棋盤擴大，研究3×3情況。

同桌研究，相互交流；教師巡視，然后請一對同桌發言。

生1：誰先到圖中2個圓圈格（如圖4），誰必勝。因為到了圓圈格對方只能向下（向左）走，這樣對方只能進必輸格，對方必輸，我必贏。

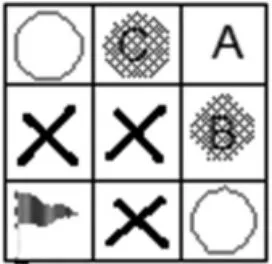
（圖4）

生 2（補充）：B、C 有兩種可能，不能保證自己必勝。但A不管怎么走都可以搶到必勝格。所以A點也是必勝格。總之，誰先搶到這三個格，誰必勝。

師：我有個疑問，我先到A，萬一對方向左下方走呢？這種情況你們沒說哦。

生：哈哈，那對方就自投羅網了。進了必輸格，必輸了呀。

（圖5）

師：好的，我們用記號“√”表示必勝格（如圖5）。誰先到必勝格，誰就有了必勝的方法。看來，只要我搶到必勝格，我肯定就贏了。

師：這么大的棋盤，我們目前只研究出這一小塊，接下來怎樣研究？有沒有更好的方法找到必勝的策略呢？

3.深究，推理標記中明確對策。

（1）自主研究：先同桌研究，接著4人小組討論，推選代表準備發言。

（2）匯報，交流

第一組匯報（邊說邊借助教師的棋盤演示）：我們接著研究了4×4情況，發現誰先到4×4外圍中任意一格，對方都能搶先到3×3外圍中的必勝格，所以4×4這一圈都是必輸格。那么5×5一圈中必有必勝格，因為每人只能走一步，所以必勝格是間隔開的，再根據方向就能確定必勝格了。以此類推，就能找到所有的必勝格了。

第二組匯報（邊說邊借助教師的棋盤演示）：我們發現1個必勝格周圍總有3個必輸格，再根據如果只從一個方向考慮必輸格后就是必勝格，能推得整個棋盤上所有的必勝格。

第三組匯報：我們是用九宮格來思考的，紅旗格其實就是一個必勝格，我們假定這個必勝格在這里，就相當于把整個九宮格一起復制，移動到這里（如圖6），這樣就能用之前的方法確定這個九宮格里的必勝格，再用這樣的方法就能找到所有的必勝格。

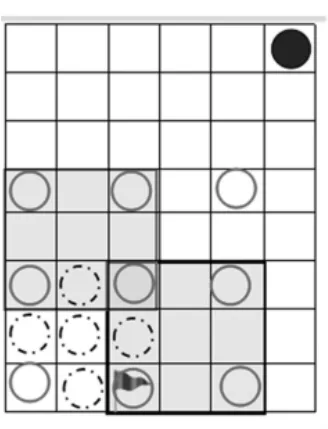
（圖6）

師：誰聽懂了他們的研究成果，他們的研究方法與第一、二組有什么不同？

生：第一、二組都是借助必輸格來推想必勝格的，第三組是借助必勝格直接推的，也就是在3×3情況的基礎上直接用模塊覆蓋的方式推理出來的。

師：變換研究基點，可以直接推理得到結果，真的非常巧妙！數學研究就是這樣，要善于借用已經研究出的成果來研究新的問題。

（3）觀察，發現

師：現在誰愿意和我玩數學棋？

生：我來下，但必須得讓我先走。

師：好的，看你小，就讓你先走。

師：為什么還沒下完棋，你們就判定他贏了？誰來解釋？

生：先走的人每一步都能搶到必勝格，所以他必勝。

師：請同桌再玩，體會體會贏的對策。

三、回顧：提煉玩棋中的收獲

師：此刻，讓我們靜下心來，回顧剛才尋找必勝對策的整個過程，你有什么特別想和別人分享的？誰能簡單地說一說？

生1：面對復雜的問題，一時不知道從哪里入手，可以從簡單的、能確定的地方開始研究。

生2：也可以在初步研究的基礎上，把這一步研究的成果打包、復制、粘貼來進行研究，這樣更快捷。

師：是的，面對復雜的問題，最好的對策就是“退”，退到最簡單又能保持原問題本質的地方開始研究，再以“退”為“進”，不斷推測、推想、推理，把簡單問題的研究成果“推”廣到更復雜的情況，從而解決問題。

【教后反思】

從教22年，筆者由最初關注教學技藝的增長慢慢轉變為關注兒童的成長，關注教兒童帶得走的數學，努力構建邏輯與直覺、理性與感性、文化傳遞與創造兼備的課堂生態，以期促進兒童成為敏于反思質疑、自省自糾、善于“悟”的人。上述教學中，筆者努力構建一個充滿自省意味的課堂，讓兒童在“退”“推”之間玩出智慧。

1.一“省”主要問題。

課始，男女生代表在擂臺賽中比拼，“純玩”中似乎全憑運氣，學霸在這里也不管用了。輸了的學生自然想再玩一次，教師并沒有立刻讓他們玩，而是利用一句“猜猜他在思考什么”引發學生思考。在“先走”還是“后走”的辯論中，在不同方案的預設中，引導學生第一次反省：有沒有必勝的策略呢？并帶領學生抓住這個主線問題開啟了探究之旅。

2.二“省”研究路徑。

真正的探究充滿未知——方向未知、路線未知、成功與否未知。怎樣讓兒童有興趣并有信心探索，即使束手無策也要努力思考，堅信也許答案就在下一個轉角呢？（1）“想一想，它究竟復雜在哪里？”學生有時會囿于困難中受傷的情緒，而并未理性思考究竟難在哪里。教師此時的點撥就顯得尤為重要。在明確困難的過程中，學生悟的方向太多，就可以分類思考；棋盤太大，就可以縮小思考范圍；步數太多，不能控制對方怎樣走棋，就從能確定的地方入手。這樣的自省活動有助于學生理清思考的方向與路徑。（2）“你們真是下到最后一步才知道輸贏的嗎？”解決問題難，并不是難在怎樣解決這個問題，而是難在“你是怎么想到的”。教師一語驚醒夢中人，讓學生明白：復雜的問題可以從簡單的、能確定的部分做起。

3.三“省”優化策略。

在思考問題的過程中，學生有時會陷入細小環節而忽略主線問題。當學生為研究清楚了2×2情況而歡呼時，教師引導他們內省：我們要找必勝的方法，卻找到了必輸點，這對我們找必勝的方法有用嗎？事實上，在曲折的研究過程中，學生需要時時問自己“這對我的研究有價值嗎？”“接下去怎樣研究？”“怎樣逼近我要尋找的答案？”在學生研究完2×2、3×3情況后，教師沒有讓學生按慣性走下去，而是以“這么大的棋盤，我們目前只研究出這一小塊，接下來怎樣研究呢？有沒有更好的方法找到必勝的策略呢？”這個問題來引導學生不斷突破思考閾限。學生或借助必輸格來推必勝格，或借助必勝格環繞3個必輸格來平鋪推理，或通過簡化方向一類一類地思考來推理，或直接將九宮格復制粘貼研究。在“復制粘貼法”出現時，學生連連發出贊嘆聲、鼓掌聲，甚至有學生由衷地說：善于利用已有的成果真重要！

4.四“省”經驗方法。

就在學生終于探得解決問題的策略，沉浸在成功的喜悅中，感受到原來秘訣如此簡單時，教師引導學生從高漲的、熱鬧的氣息中抽離出來，靜思探索過程，用簡單的語言分享收獲。讓學生悟得：面對復雜的問題，可以退到最簡單而又不失其本質的地方，從能確定的簡單之處入手尋找方法，再以探得的成果為基礎，不斷推想、推測、推理，從而化復雜為簡單，最終成功地解決問題。

總之，在“玩”的過程中，學生一次次跌倒思考，又一次次起身前行，在“退”“推”之間，玩出了智慧。