基于比例系數-有效獨立法對圓柱殼聲輻射預報的測點優化布置研究

余 鵬，陳美霞，謝 坤

（華中科技大學 船舶與海洋工程學院，武漢430074）

0 引言

圓柱殼結構作為潛艇的主要組成部分，對其振動響應及輻射聲場的研究具有重要科學意義和實用價值。如何合理布置圓柱殼上的一系列傳感器來對殼體的振動響應進行監測和預報，進而進行針對性的控制就顯得非常重要。

目前針對圓柱殼結構的傳感器優化布置，主要有兩種方法：一是文獻[1]中提出的均勻布置方法，即沿圓柱殼周向和軸向等間距地布置一系列測點，通過分析不同間距時得到的預報結果確定合適的測點布置方案。隨后，大部分學者[2-4]均是采用的均勻測點布置方法，這種方法雖能得到準確的預報結果，但對測點數目要求較高，且在測點位置的選取上具有很大的盲目性和主觀性；二是文獻[5]中以模態矩陣的條件數為目標函數，采用逐步削減的方法確定測點布置方案。這種方法可有效地避免測點選取的不確定性，但對于頻段較高時的振動響應預報，因其模態密集，很難得到準確的模態信息，從而對振動響應結果產生很大的誤差。

Kammer[6]在對大型空間結構傳感器優化布置研究中提出的有效獨立法（effective independence，EI）是目前應用最廣泛的方法之一。其基本思想是按照各待選測點對目標模態矩陣線性獨立性貢獻大小進行排序，以優化Fisher 信息矩陣，用迭代的方法逐步刪除線性獨立貢獻量小的測點位置，直至達到指定的測點數。針對不同類型的結構，眾多學者在有效獨立法的基礎上進行了不同的改進，如Meo[7]提出了用單位剛度的模態應變能作為驅動點殘差系數的有效獨立-驅動點殘差法，楊雅勛[8]提出了以模態應變能反映目標矩陣最大線性無關性的能量系數-有效獨立法等等。

對于本文中的圓柱殼結構，由于其振動模態的對稱性及反對稱性，此時對稱和反對稱位置，或間距較小的節點可能對模態矩陣線性獨立性的貢獻都很大，但是這兩者往往提供的是重復的信息。若利用傳統有效獨立法，逐步刪除對模態振型貢獻小的候選測點，就不可避免地產生所選測點的信息冗余問題。基于此，本文用模態振型比例系數評價兩測點間的信息獨立程度，提出了一種能夠同時滿足所選測點模態可測性和避免信息冗余性的測點優化布置算法。

本文依據模態疊加原理，將水下結構的振速場在干模態空間中展開。利用比例系數-有效獨立法得到的測點布置方案，與均勻布置方法[1]、基于條件數法[5]及傳統有效獨立法[6]得到的測點布置方案進行對比。結果表明，對于圓柱殼結構，比例系數-有效獨立法更好地保留了結構的振動模態信息，且聲振響應預報的精度更高，是一種更優的測點布置方法。

1 基本理論

1.1 模態疊加理論

對于水下彈性結構的振動響應，其運動方程為：

式中：M、C 和K 分別為結構的質量矩陣、 阻尼矩陣和剛度矩陣，p（t）為流體與結構交界面上由于結構振動引起的流體載荷，f（t）為除了p（t）以外的外界激勵，x（t）為結構各節點位移向量。

經Laplace 變換后，得到結構頻域中的振動表達式為：

根據模態疊加的原理[9]，可將結構振速在干模態空間中進行展開：

式中：V 為結構各節點的速度矢量，φr為結構在空氣中的第r 階振型，qr為第r 階模態坐標。

結構節點的速度矢量與位移矢量的關系如下：

由模態正交性，結合（2）-（4）式可得：

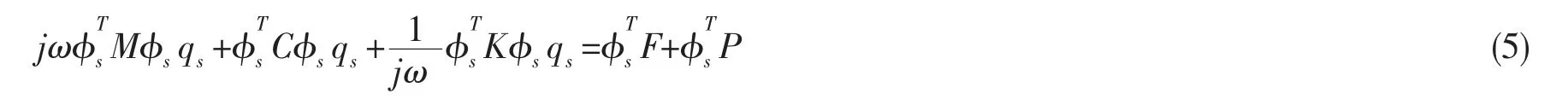
由此，可得第S 階模態坐標為：

（6）式表明，將水下結構的振速在干模態空間中展開是合理的，將流體載荷作為外部激勵力，流體載荷只對模態坐標有影響。

由（5）式可知，無阻尼結構在空氣中自由振動的動力學方程為：

式中：ωr是結構在空氣中的固有頻率。對（7）式進行質量歸一，即可得：

將上式代入（7）式，可得：

當結構在水中振動時，流體介質對結構振動的影響可以表示成附加質量的形式，則（7）式可變為：

式中：Δms是模態附連水質量，ωs是結構水中模態的固有頻率。

結合（8）-（10）式，可得結構在空氣和水中固有頻率的換算公式如下：

（11）式表明，根據邊界元離散得到的模態附連水質量，即可對結構在每階振型下的空氣和水中固有頻率進行換算。

在中、低頻段范圍內，由于高階模態對結構振動響應影響很小，所以可以采用模態截斷的方法，忽略高階模態的影響。根據振動響應分析的最高頻率及固有頻率的換算公式，可得結構在空氣介質中進行模態分析的最高頻率，從而得到模態截斷階數N。假設可選測點總數為n，則（3）式可寫成矩陣形式為：

利用有效獨立法從可選測點總數n 中選擇M 個節點作為測點，可得到結構表面M 個測點的法向速度：

根據上式，可以用M 個測點的法向振速通過逆向求解得到前N 階模態坐標[q]N×1，進而對結構的整個表面的振速場進行重構。

分析（13）式構成的線性方程組，當M＜N 時，（13）式為欠定方程組，[q]的解不唯一。故為了使[q]有唯一確定的解，要求測點數目至少與模態截斷數目保持相等。

1.2 有效獨立法基本理論

考慮白噪聲影響，（12）式可表示為：

式中：υ 是方差為σ2的高斯白噪聲。

有效獨立法的基本理論是保證傳感器能夠得到盡可能多的線性無關的模態信息，實際上即是對模態坐標q 的最佳估計[11]。對應于q 存在偏差，假設（q為q 的無偏有效估計，估計偏差的協方差矩陣P可表示為：

式中：Q 為Fisher 信息矩陣[6]。

假設每個傳感器的檢測噪音誤差都是相互獨立且每個傳感器的統計特性都是一致的，那么Fisher信息矩陣可以描述如下：

式中：A0=ΦTΦ。由上式可知，矩陣A0越大則協方差矩陣P 越小，即當A0最大時可獲得q 的最佳估計。

矩陣A0的特征方程為：

式中：Ψ 是Q 的標準化特征向量，λ 是相應的特征值。

構造矩陣ED=ΦΨλ-1（Φ Ψ）T，可得：

矩陣ED對角線上的第i 個元素表示第i 個測點對模態矩陣線性無關性的貢獻。有效獨立法通過ED矩陣對角元素的大小對各個候選測點的優先順序進行排序，用迭代算法每次排除ED對角元素最小的候選測點位置，再進行下一次的迭代，直至得到滿意的布置點數[13]。

1.3 比例系數-有效獨立法基本理論

盡管利用傳統有效獨立法可有效地估計結構的振動特性，但是它忽略了兩個待選測點有相似的Fisher 信息矩陣的情況[12]。此時，雖然每個待選測點對模態矩陣線性獨立性的貢獻都很大，但是如果他們的信息矩陣是基本相同的，那么選擇這兩個測點得到的結構模態信息量和選擇一個是基本相同的。

針對上述問題，本文定義模態振型比例系數為兩個節點模態向量間的余弦值，用來評價測點之間的信息獨立性，即：

式中：φi和φj分別為第i 和第j 個測點提供的模態振型，即模態矩陣的第i 行和第j 行，N 為模態截斷數目。對于布置方案中任意兩個測點，均滿足：

當lij為0 時，說明兩個測點提供的信息矩陣是相同的，則選擇這兩個測點得到的結構模態信息量和選擇一個是相同的；當lij為1 時，兩個測點提供的信息矩陣相互獨立。

本文采用逐步累加的方式求解比例系數-有效獨立法，以得到同時滿足所選測點模態可測性和避免信息冗余的測點優化布置方案。具體步驟如下：

（1）首先按照（18）式計算出每個待選測點對模態矩陣線性無關性的貢獻并排序，選擇貢獻量最大的待選測點作為第1 個測點位置。

（2）按照（19）式計算第1 個測點與剩余n-1 個待選測點之間的模態振型比例系數，選擇比例系數最小值對應的待選測點作為第2 個測點位置。

（3）分別計算已選2 個測點與剩余n-2 個待選測點之間的模態振型比例系數，得到兩個數組l1和l2。計算l1和l2中對應元素的均方差，選擇均方差最小值對應的待選測點作為第3 個測點。如此，第3個測點與已選2 個測點的模態振型均能保持較大的線性無關性。

（4）重復步驟（3），直到確定全部M 個測點的位置。得到基于比例系數-有效獨立法的圓柱殼測點優化布置方案。

1.4 測點布置方案評價準則

要判別一個測點布置方案的優劣，需要建立相應的評價標準，從而可以對測點布置方案進行評價[14]。下面分別從振動模態和響應的角度對評價準則進行介紹。

（1）基于振動模態的評價準則

由結構動力學原理可知，結構各固有振型在節點上的值形成一組正交向量，但由于量測的自由度遠小于結構模型的自由度，且受外界環境的影響，測得的模態向量不能保證其正交性，甚至會由于向量間的空間夾角過小而丟失重要的模態。因此，在選擇測點時有必要使測量的模態向量保持較大的空間夾角，從而盡可能地把原來模型的特性保留下來。

模態保證準則MAC（Modal Assurance Criterion）矩陣[15-16]是評價模態向量空間夾角的一個很好的工具，其公式表達如下：

式中：φi和φj分別為第i 階和第j 階模態向量。當MAC 矩陣中的某一元素等于1 時，表明這兩階模態向量空間夾角為零，其對應的模態振型不可分辨；當MAC 矩陣中的某一元素為0 時，表明這兩階模態向量相互正交，其對應振型可輕易識別。于是通過檢查各階振型在量測自由度上形成的MAC 矩陣的非對角元，即可判斷出相應兩個振型向量的夾角情況。

（2）基于振動響應的評價準則

測點優化布置的一個重要目的是為了能利用有限測點的響應來構造未測量點的響應。根據（3）式，可以用M 個測點的法向振速通過逆向求解得到前N 階模態坐標[q]N×1，進而對結構整個表面的振速場進行重構。由于振動結構的輻射聲場可由表面振速分布唯一地確定，通過聲輻射邊界元方法求得流體介質中的聲傳遞矢量ATV（Acoustic Transfer Vector），即可得到聲場中某一點輻射聲壓[10]。故本文以均方振速及場點輻射聲壓的結果對比來評價每種測點布置方案，均方振速及輻射聲壓的計算公式分別如下：

通過對比聲場中某一點輻射聲壓的計算結果與預報結果，也可驗證本文中的測點布置方法的可行性和有效性。

2 數值分析

本文以水下典型結構-單層加筋圓柱殼為研究對象。結構參數：總長L=1.02 m，半徑R=0.425 m，肋骨間距l=0.075 m，環肋截面尺寸4 mm×33 mm，殼體厚t=0.004 m。材料參數：密度ρ=7 800 kg/m3，彈性模量E=210 GPa，泊松比μ=0.3，阻尼比ξ=0.005。

建模的坐標原點均位于模型左端面的中心，x、y、z 分別為水平、垂向和軸向。邊界條件為結構兩端約束x、y 兩個方向上的平動，激勵力為垂向單位力，激勵力位置坐標為（0，-0.425，0.525），場點坐標（0，-100，0.525）。分析頻率為0-1 000 Hz，間隔5 Hz。結構的周向和軸向網格數分別取為144 和56，節點總數為8 208。

圖1 單層圓柱殼結構圖Fig.1 Single-layer cylindrical shell

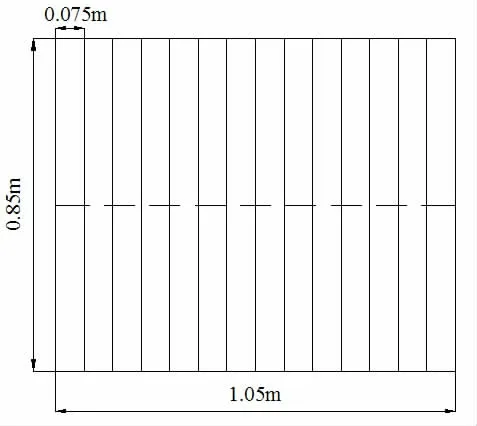
圖2 單層圓柱殼尺寸圖Fig.2 Dimension figure of cylindrical shell

2.1 模態分析

對上述圓柱殼結構進行模態分析及頻率換算可知，將結構在空氣中的振動模態從第64 階截斷即可滿足水中振動響應分析的最高頻率1 000 Hz，故模態截斷數目需至少取為64。由于篇幅有限，并考慮到結構振動對稱模態與反對稱模態，表1 僅列出了結構第62～70 階振動模態及對應的換算頻率（m為軸向半波數，n 為周向波數）。

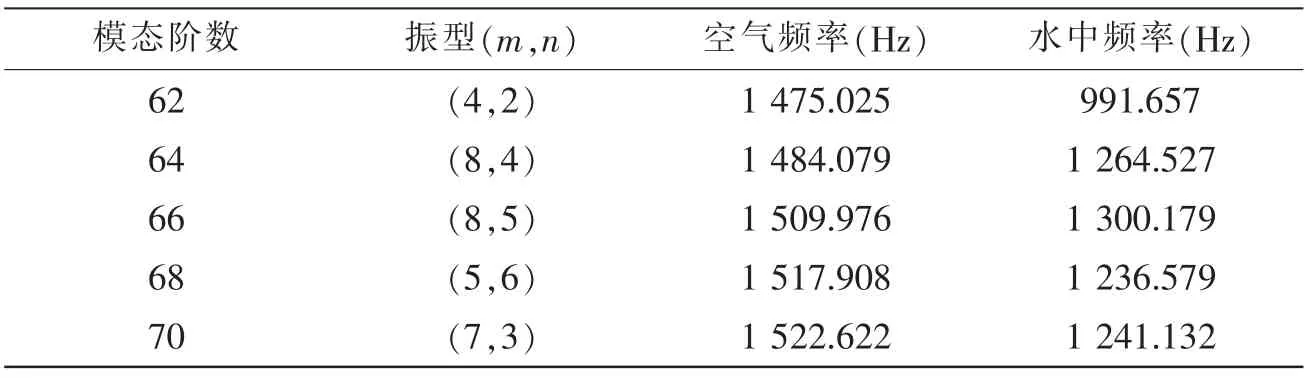
表1 固有頻率換算表Tab.1 The conversion table of natural frequency

2.2 測點布置方案

根據上述理論分析，為使（13）式得到唯一確定的解，本文選取的測點數目與結構模態截斷數目保持相等，即測點數目取為64。忽略結構邊界處的節點，以剩下所有節點作為待選測點，則待選測點總數為7 920，故需從7 920 個待選測點中選取64 個作為測點。均勻測點的一種布置見圖3所示（由于均勻測點布置方式的多樣性，本文選擇了多種布置方式中預報結果最好的一種作為對比），基于條件數的測點布置見圖4所示，傳統有效獨立法得到的測點布置見圖5所示，本文方法得到的測點布置見圖6所示。

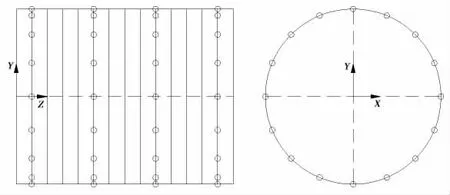
圖3 均勻布置方法Fig.3 The uniform sensor displacement

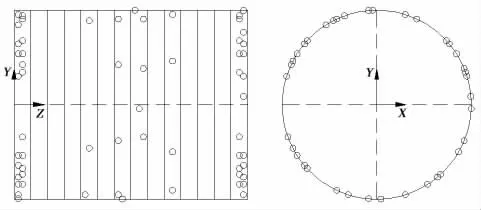
圖4 基于條件數法Fig.4 Sensor displacement based on conditional number

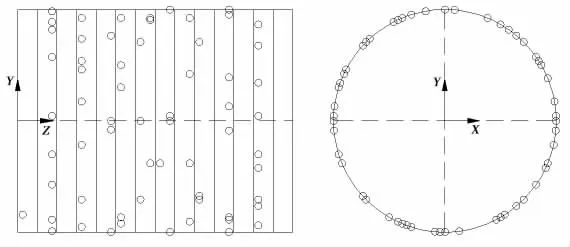
圖5 傳統有效獨立法Fig.5 Sensor displacement based on original EI

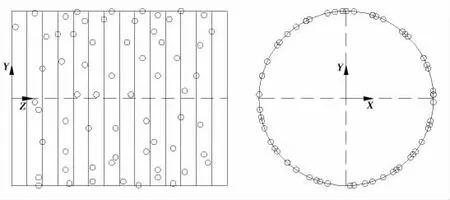
圖6 本文方法Fig.6 Sensor displacement based on this paper

2.3 方案評價

下面分別從振動模態和響應的角度對上述測點布置方案進行評價。

（1）基于振動模態的評價準則

根據上述理論分析，MAC 矩陣的非對角元越小，所選測點的模態向量的空間夾角就越大，各階模態向量就越容易被識別。上述四種測點布置方案對應的MAC 矩陣分別如圖7-10所示，其中兩水平軸代表模態階次，垂直軸代表MAC 矩陣非對角元值，對角元素全部置為0。從圖中可以看出，四種測點布置方案對應的MAC 矩陣非對角元的最大值分別為0.999 4、0.788 1、0.179 4 和0.165 6，其平均值分別為0.005 0、0.011 4、0.002 3 和0.001 8。并且，根據（21）式求得四種測點布置方案的模態振型比例系數的最大值分別為0.667 5、0.999 8、0.825 4 和0.4。可見，對于圓柱殼結構，采用本文中的比例系數-有效獨立法得到的測點模態向量在保留結構的振動特性方面具有明顯的優勢。

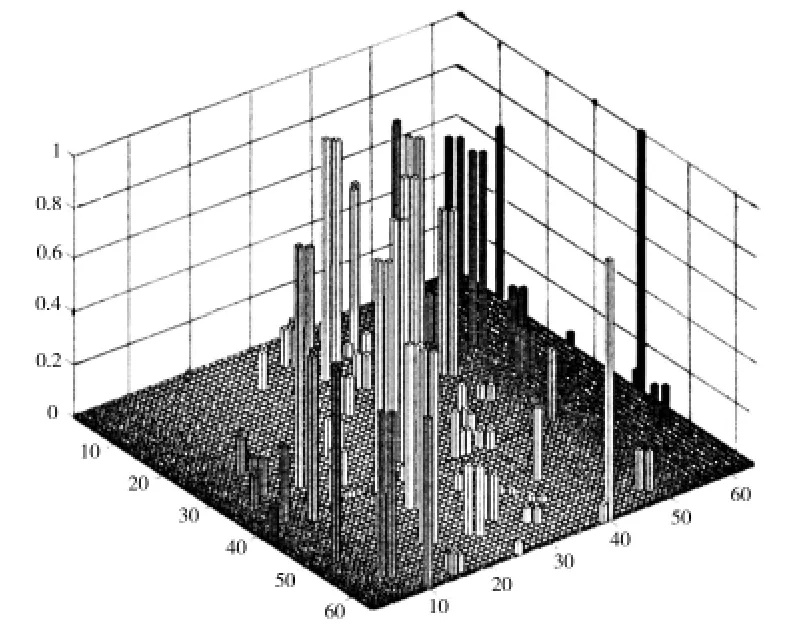
圖7 均勻布置方法Fig.7 The uniform method

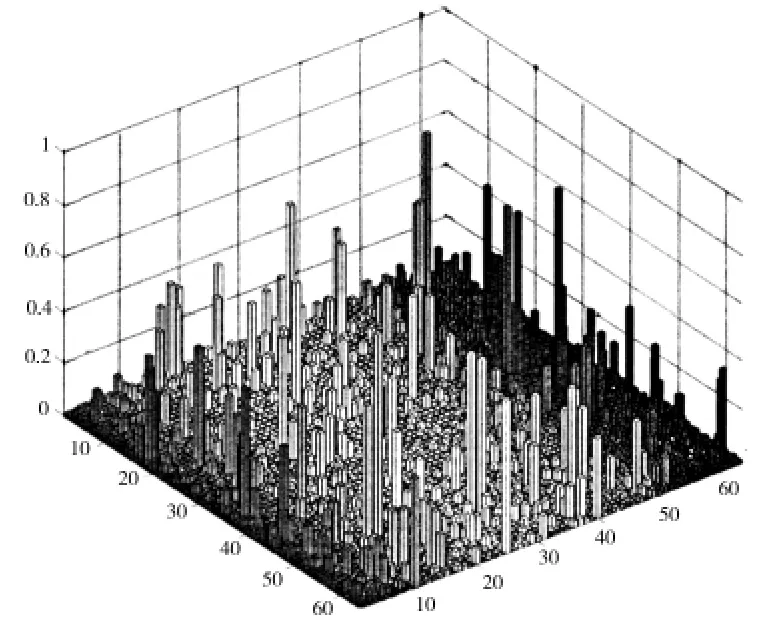
圖8 基于條件數法Fig.8 Method based on conditional number

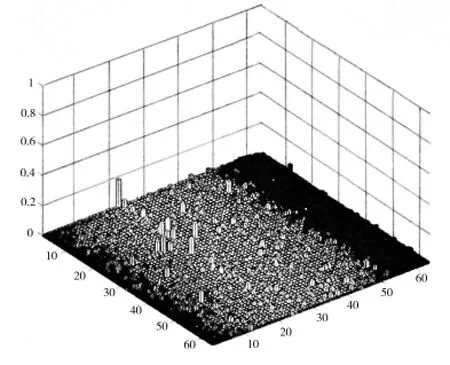
圖9 傳統有效獨立法Fig.9 The original EI method

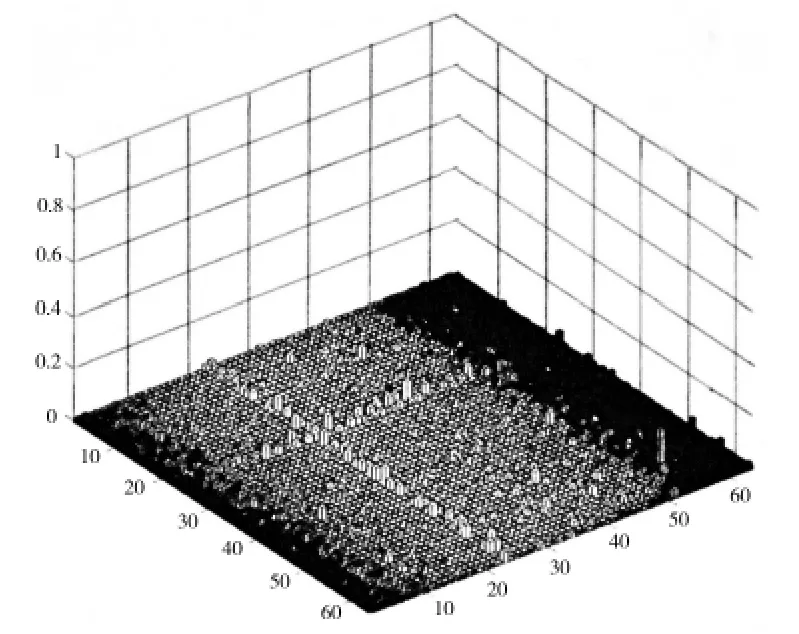
圖10 本文方法Fig.10 Method of this paper

（2）基于振動響應的評價準則

由上述四種測點布置方案，得到結構均方振速及場點輻射聲壓的計算結果與預報結果的對比曲線如圖11-12所示。從圖中可以看出，采用均勻布置方法雖能得到較好的預報結果，但在測點選取上具有一定的盲目性，需要大量的計算和分析對比；基于條件數法在較低的頻段內預報精度較高，但隨著頻率的增加，誤差會相應增大；傳統有效獨立法在較高頻率段內也會產生較大的誤差，而本文方法得到的預報結果精度最高。進一步說明了本文方法是一種有效的測點優化布置算法。

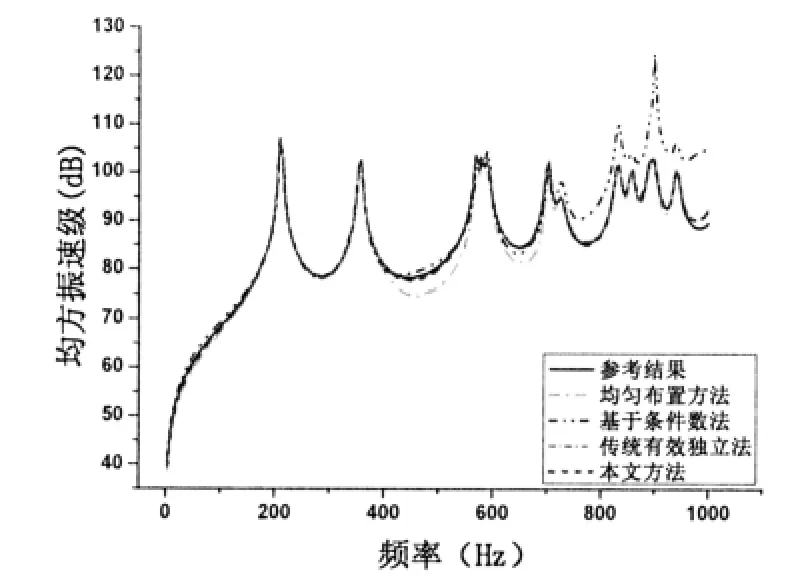
圖11 法向均方振速級Fig.11 Normal mean-square-velocity

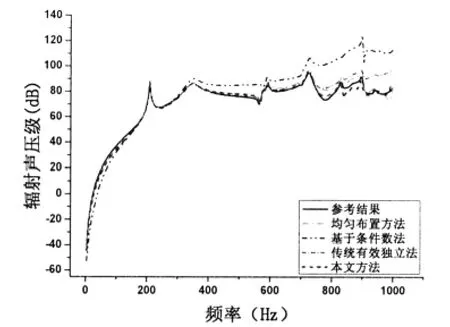
圖12 場點輻射聲壓級Fig.12 Radiated sound pressure of field point

3 結論

本文針對圓柱殼結構的測點優化布置進行研究，并得到以下結論：

（1）在對傳統有效獨立法研究的基礎上，提出了基于比例系數-有效獨立法的測點優化布置算法，其以反映測點之間模態振型比例系數進一步優化了測點的選取。

（2）對比均勻布置方法、基于條件數法以及傳統的有效獨立法，本文方法得到的測點布置方案用基于模態和響應的準則進行評價的結果都很好。既能保證測量振型向量的正交性，又能對聲振響應結果進行準確的預報。所以，本文提出的方法是一種有效的測點優化布置方法。