超音速來流中爆轟波衍射和二次起爆過程研究*

李紅賓，李建玲，熊 姹，范 瑋，趙 磊，韓文虎

（1.西北工業大學動力與能源學院，陜西 西安 710072；2.陜西省航空發動機內流動力學重點實驗室，陜西 西安 710072；3.北京理工大學爆炸科學與技術國家重點實驗室，北京 100081）

爆轟燃燒具有化學能釋放速率快、化學反應區短、自增壓等特點[1]，因此爆轟燃燒方式在高超聲速推進領域有很好的應用前景。為了將爆轟燃燒應用于高超聲速推進器中，Alexandrov等[2]提出超聲速脈沖爆轟沖壓發動機的構想，Wilson等[3]提出了脈沖正爆轟波發動機概念。其原理是當燃燒室進口氣流速度小于爆轟波傳播速度時，可利用在超聲速流中逆流前傳的非穩態正爆轟波來產生推力，而無需將高超聲速來流減速至亞聲速。Li等[4]從燃燒熵增的角度揭示了基于逆流傳播的正爆轟波發動機的理論優勢，并給出其優勢飛行馬赫數范圍約為3～7。

盡管超聲速爆轟發動機是極具前景的高超聲速飛行器動力備選方案，但上述概念的成功實現都必須建立在對管內超聲速流中爆轟機理的深入認識，尤其是掌握如何在超聲速來流中成功起始逆流傳播的正爆轟波。但是相比于靜止和亞聲速來流，在超聲速流中采用低能點火來起始爆轟波的難度更大。在工程應用領域，預爆管起爆技術被廣泛地應用于各型爆轟發動機的起始中，即利用在小尺寸預爆管中形成的爆轟波來起始大尺寸的主爆轟室中的爆轟波。而較之低能點火后爆燃向爆轟轉變的起爆方法，在超聲速流條件下使用預爆管技術來起始主爆轟室內的爆轟波顯然是一種更可靠的起爆方式，并且已被成功運用。例如在熱射式超聲速風洞中，Vasil'ev等[5]使用乙烯/氧氣預爆管作為點火裝置，在氫氣/空氣超聲速混氣流中成功起始了向上游逆流傳播的爆轟波以及向下游順流傳播的爆轟波。Ishii等[6]用激波管來驅動超聲速來流，利用預爆管向激波管內的超聲速混氣流中橫向噴注爆轟波，同樣成功起始了爆轟波。

在靜止氣流中，當爆轟波從預爆管內的受限空間傳播進入突擴空間時，爆轟波的衍射和隨后可能發生的二次起爆現象是起爆過程的核心問題，并且在工程應用領域和學術界已經有大量的文獻[7-9]報道過氣相爆轟中的衍射和二次起爆規律。一般來說，當爆轟波發生衍射時，前導激波和化學反應面會逐漸解耦。而其二次起爆過程一般會根據燃燒室的幾何構型分為兩種機制[10]：在半無限空間中的自發二次起爆和管道內反射波后的二次起爆現象。在自發二次起爆過程中，存在臨界起爆管徑dc[9]，即入射管道的直徑小于dc時，便不能發生二次起爆現象，否則二次起爆成功。對于不穩定爆轟（對應于不加稀釋氣體的可爆混合物，爆轟波胞格結構不規則）其臨界管徑dc≈13λ[9]（λ為爆轟波胞格大小）；而對于穩定的爆轟波（對應于用惰性氣體高度稀釋過的可爆混合物，爆轟波胞格結構非常規則）其臨界管徑dc可增大至30λ或者更大[9]。此外，在反射波后二次起爆的過程中，爆轟波可借助與另一側壁面的反射作用來觸發二次起爆現象。

然而，超音速來流中爆轟波的起爆和傳播問題目前還并未被深入地研究。基于此，本文中采用數值模擬方法，研究橫向的超音速來流對爆轟波衍射和二次起爆過程的影響。所模擬的爆轟波具有規則的胞格結構，對應于用惰性氣體高度稀釋的可爆混合物中形成的爆轟波。研究橫向超音速來流對半無限空間內爆轟波的衍射和自發二次起爆以及管道內的衍射和壁面反射二次起爆兩種現象的影響，并與靜止氣流中爆轟波的衍射和二次起爆現象進行對比。

1 數值方法和物理模型

1.1 數值方法

采用帶化學反應源項的二維無黏Euler方程組來描述爆轟過程。關于爆轟波的數值模擬，國防科大Cai等[11]使用無黏的Euler方程組和帶黏性的NS方程組數值模擬了爆轟波的傳播過程，指出盡管加入黏性能更準確地模擬爆轟波的結構，但是采用Euler方程組也可以得到定性上一致的結論。另外Gallier等[12]使用Euler方程組模擬得到了與實驗一致的爆轟波衍射過程。鑒于此，本文中也忽略黏性對爆轟波的影響。為了引入兩步支鏈化學反應機理，本研究中加入變量α和β來分別表示誘導步和反應步的進程參數，守恒形式的控制方程如下：

式中：U表示守恒向量，E和F分別表示對流通量，S為化學反應源項。

采用兩步支鏈化學反應模型[13]，其中誘導步為一個熱中性的化學反應，且化學反應速率對溫度敏感。在誘導區后是能量快速釋放的化學反應區，其具體的反應速率表達式為：

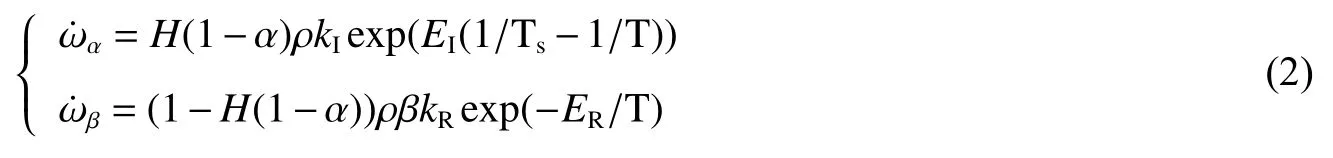
式中：Ts為激波后未反應氣體的溫度，EI和ER代表活化能，kI和kR代表反應速率常數。反應模型中的開關函數表達式為：

采用基于有限差分的五階精度的加權無振蕩[14](WENO)格式對控制方程進行數值離散，以便精確捕捉流場中各激波及它們之間的相互作用過程。空間分裂采用常用的Lax-Friedrichs(LF)[15]方法對各守恒變量進行分裂，并采用三階Runge-Kutta方法進行時間方向上的離散。由于研究中采用較細的均勻網格（誘導區內約8個網格點）和時間步長（CFL數為0.3）進行模擬，計算量較大。為了加速計算，采用基于消息傳遞接口的MPI(message passing interface)方法進行并行化處理，以獲得較快的計算速度。

1.2 物理模型

分別研究半自由空間和管道內爆轟波的衍射和二次起爆過程。圖1為采用的兩種物理模型，平面爆轟波從預爆管中衍射進入超聲速氣流中，而超聲速氣流從左側進入計算區域。在壁面反射的計算模型中，使用對稱壁面條件來模擬反射作用對爆轟波衍射和二次起爆過程的影響。

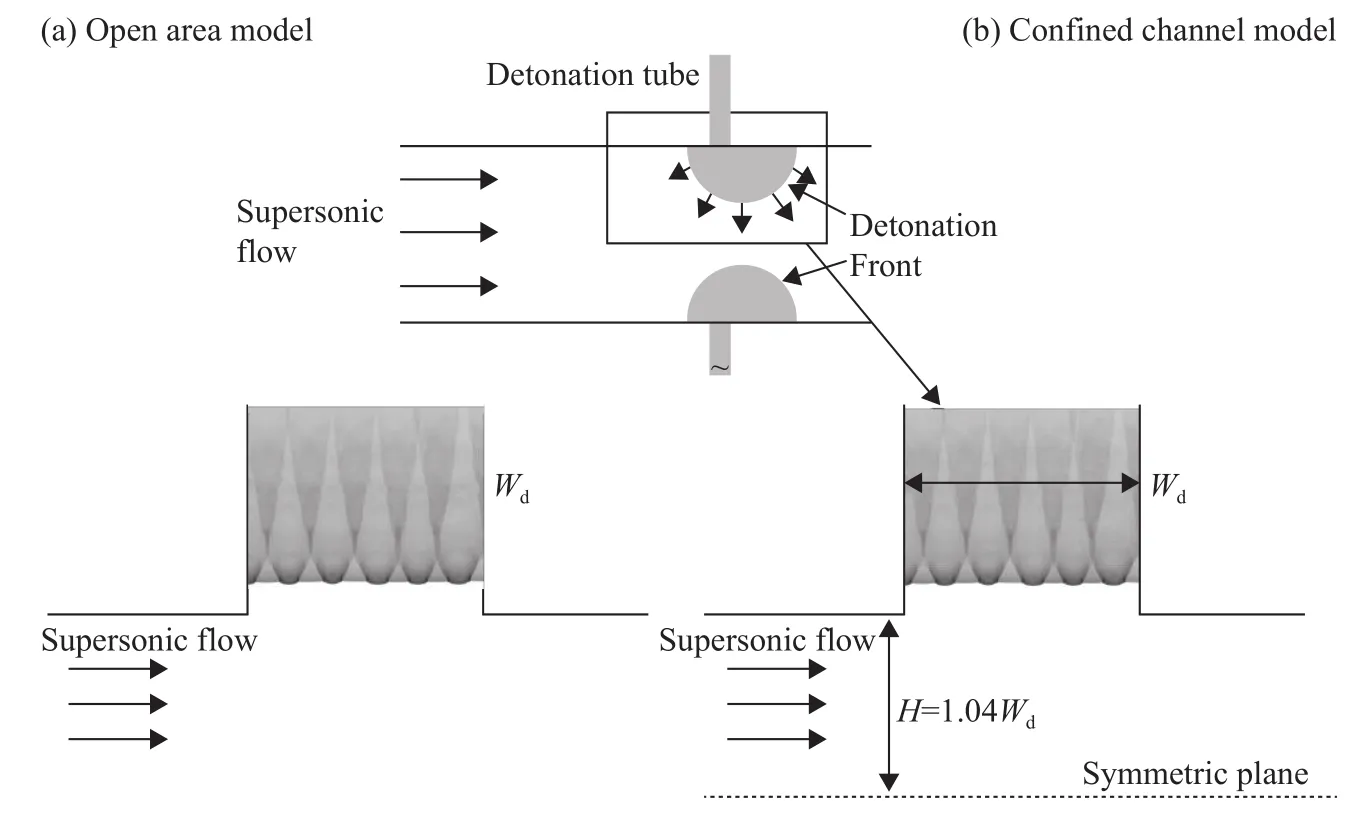
圖1 物理模型Fig.1 Physical model

本文中研究的爆轟波為穩定爆轟波[13]，對應于用惰性氣體高度稀釋過的可爆混合物，其特征是具有規則胞格結構。并且計算開始時，在預爆管內初始化了一道穩定的平面爆轟波，如圖1所示。文中爆轟波的穩定性是通過控制不穩定性參數χ[13]來獲得的：χ值越大，爆轟波的胞格結構越不規則，對應未加稀釋氣體的可爆混合物形成的爆轟波；反之越規則，對應用惰性氣體高度稀釋過的可爆混合物形成的爆轟波。需要特別說明的是，無論可爆氣體是否經過稀釋，所形成的爆轟波本質上都是高度不穩定的，如波面脈動的橫波結構等。而本文關于穩定與不穩定爆轟波的敘述只是相對的概念，并且相關的文獻[13,16]也有類似的敘述，所以本文中也沿用了這一定義。

本文中使用的化學反應模型的主要參數均采用無量綱化[13]處理，具體取值為：放熱量Q=21.7，活化能EI=4.8Ts，ER=1.0Ts，其中誘導步反應速率參數kI=uvn，uvn為激波后氣體的粒子速度，這樣設置可以令誘導區長度Lin=1.0。而反應模型中速率常數kR的選取直接關系到χ值的大小，本文中kR的取值為1.439kI，對應的不穩定性參數χ=0.698，其具體的計算方法可參考文獻[13]。本文數值模擬得到的爆轟波的規則胞格結構如圖2所示。

圖2 穩定爆轟波的規則胞格結構Fig.2 Cellular structures of regular detonation wave

1.3 數值模擬驗證

為了驗證數值模擬的可靠性，選擇爆轟波胞格大小進行驗證，主要是在靜止氣流中驗證胞格大小與管徑的關系。數值模擬的網格密度為誘導區Lin內8個網格點，并且在此網格密度下得到了比較可靠的爆轟波胞格結構。圖3給出了爆轟波在兩個不同管徑下得到的胞格結構，在這兩種管徑下均得到了穩定的胞格結構。兩種管徑下模擬得到的爆轟波胞格大小分別為53.57Lin和53.12Lin，比較接近。

圖3 不同管徑下的爆轟波胞格結構Fig.3 Detonation cellular structures in channels with different widths

此外，還計算了在其他管徑下爆轟波的胞格結構，其中所選擇的管徑大小與爆轟波胞格大小的比值約為4.7。管徑大小既非整數倍的胞格，又非整數倍加半個的胞格，因此兩者并不匹配。圖4給出了管徑與爆轟波胞格大小不匹配時的結果，在此種情況下無法得到規則的胞格結構。需要特別說明的是，圖4中的不規則胞格結構并不是爆轟波自身不穩定性（即不穩定性參數χ比較大時爆轟波所表現出來的不穩定性）的表現，而是胞格大小與管徑不匹配造成的，爆轟波依然是穩定的爆轟波。綜上所述，本文的數值模擬可以得到比較可信的胞格大小，同時也能說明本文的數值模擬能夠給出合理的結果。

圖4 管徑與爆轟波胞格大小不匹配時的胞格結構Fig.4 Cellular structures of detonation wave when the channel width is inappropriate

2 結果與討論

2.1 超聲速來流條件對半自由空間內爆轟波衍射過程的影響

在半自由空間中，爆轟波的二次起爆成功與否完全依靠衍射進入半自由空間內的爆轟波自身的能量，并無壁面反射的促進作用。圖5給出了爆轟波傳播進入半自由空間中的衍射過程。由圖可知平面爆轟波從二維管道中進入半自由空間后，首先形成了一個三角形的核心流區域，在此區域內傳播的爆轟波未受側向的膨脹波削弱，其胞格結構和未發生衍射時相似，如圖5中紅色虛線所示。而在核心的三角流動區域外，波面也會生成新的橫波結構，并產生橫波碰撞現象，如圖5中紅色箭頭所示。由于橫波碰撞的增強作用，爆轟波的自持傳播距離進一步得到拓展。但是在本文所研究的工況下，衍射爆轟波在靜止氣流中最終熄滅。

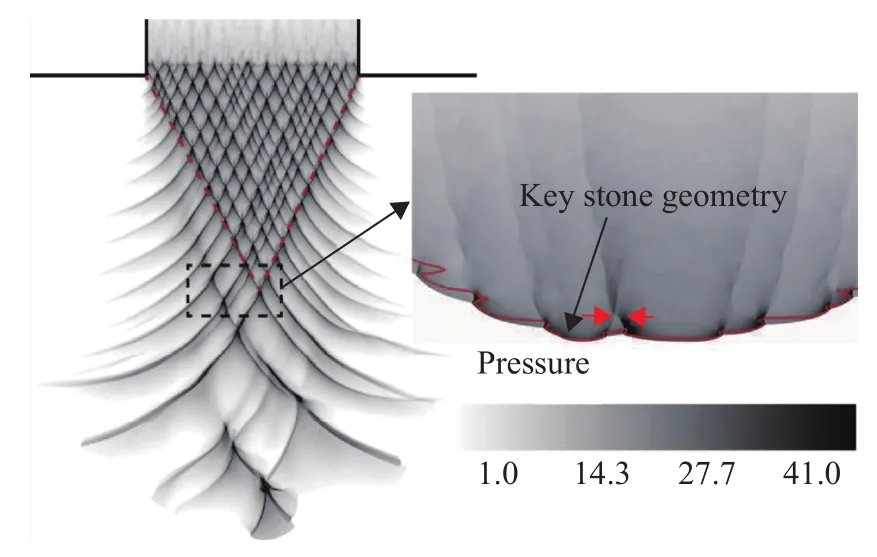
圖5 爆轟波在半自由空間內的靜止氣流中的衍射現象Fig.5 Diffraction of detonation wave in the static flow

相比于靜止氣流中爆轟波的衍射過程，當流場中加入超音速氣流后，爆轟波的衍射和二次起爆現象得到較大的改善。主要原因是在核心流的三角區域外，產生了更多的橫波碰撞現象，爆轟波的自持傳播距離也被大大拓展，如圖6(a)所示。超音速氣流從左側進入流場，與衍射出來的爆轟波相互作用，從圖6(b)中的流線圖可以看出，逆流側的氣流明顯受到壓縮作用，氣流的衰減過程在一定程度上被抑制，因此在逆流側持續誘導產生了橫波結構，爆轟波的自持傳播距離也更遠。

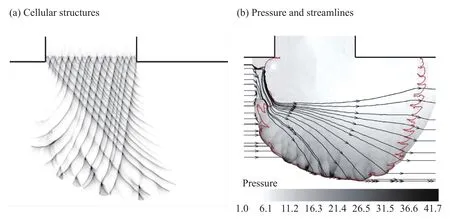
圖6 爆轟波在超音速氣流(Ma=2.0)中的衍射過程（紅線近似表示火焰面位置）Fig.6 Diffraction process of detonation wave in the supersonic (Ma=2.0) flow (the red line indicates the flame front)

圖7 爆轟波在超音速氣流(Ma=4.0)中的衍射過程（紅線近似表示火焰面位置）Fig.7 Diffraction process of detonation wave in the supersonic (Ma=4.0) flow (the red line indicates the flame front)

隨著來流馬赫數的進一步提高，爆轟波在逆流側受到的超音速氣流的壓縮作用增強。因此爆轟波進入超音速氣流后，核心流區域之外產生了更多、更強的橫波碰撞現象（即胞格結構），如圖7(a)所示。但是在半自由空間中，當爆轟波遠離入射管出口后，靠近上壁面處的爆轟波的強度依然會衰減，并出現了明顯的解耦現象，如圖7(b)中的爆轟波壓力云圖所示。相比于Ma=2.0的超音速氣流中的衍射過程，爆轟波自持傳播的距離進一步增加，但是也能明顯看出胞格大小λ是逐漸增加的，因此可以預見爆轟波最終還是會衰減并熄滅。而在穩定爆轟波（氣相）的衍射過程中[9]，當平面爆轟波的強度足夠強（入射管直徑大于臨界管徑dc）時，爆轟波基本不受兩側膨脹波的削弱，即核心流區域基本上保持等寬度向前傳播。然而在本文所模擬的尺度下，在超音速氣流中，盡管爆轟波的傳播距離得到有效地拓展，但是也并未能成功地在主流中發生二次起爆。在更大的幾何尺寸中，橫向超音速來流對爆轟波衍射過程的影響還需進一步研究。

2.2 超音速來流條件對管道內爆轟波衍射和二次起爆過程影響

為了探究受限空間內爆轟波在超音速來流中的二次起爆機理，詳細比較了管道內靜止氣流和超音速氣流中爆轟波的二次起爆過程。圖8給出了超音速流動條件下爆轟波衍射和二次起爆的結果，加入超音速氣流后，爆轟波的二次起爆過程被完全改變了。在靜止氣流中爆轟波不能成功二次起爆，而在超音速氣流中(Ma=2.0)爆轟波成功實現了二次起爆。本文中重點關注了逆超音速來流側的二次起爆過程，順流側二次起爆現象并未考慮。并且當爆轟發動機[3]工作在燃燒室進口來流速度小于爆轟波傳播速度的飛行條件時，爆轟發動機是利用逆流前傳的爆轟波來進行工作的。下面將進一步討論管道內超音速來流條件對爆轟波二次起爆過程的影響。

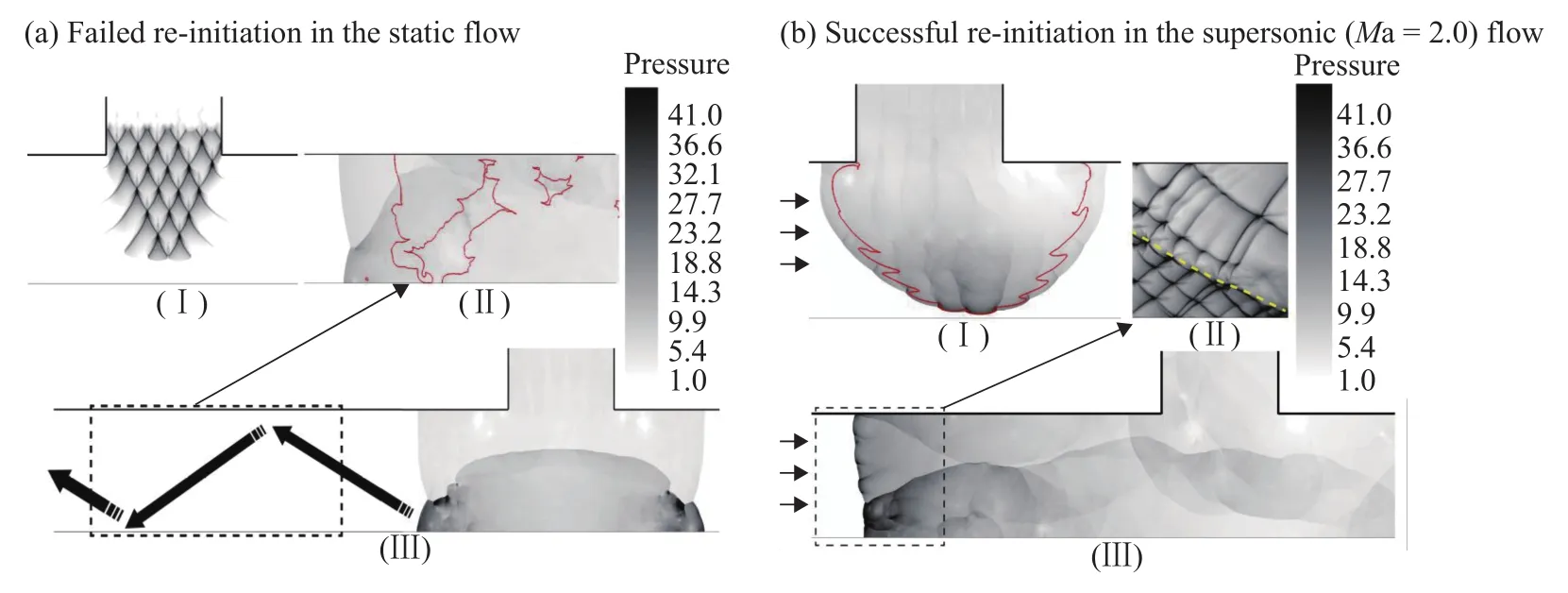
圖8 爆轟波在靜止氣流和超音速氣流中的衍射過程（紅色細實線近似表示火焰面位置）Fig.8 Diffraction and re-initiation processes of detonation wave in the static and supersonic flow(the red line indicates the flame front)

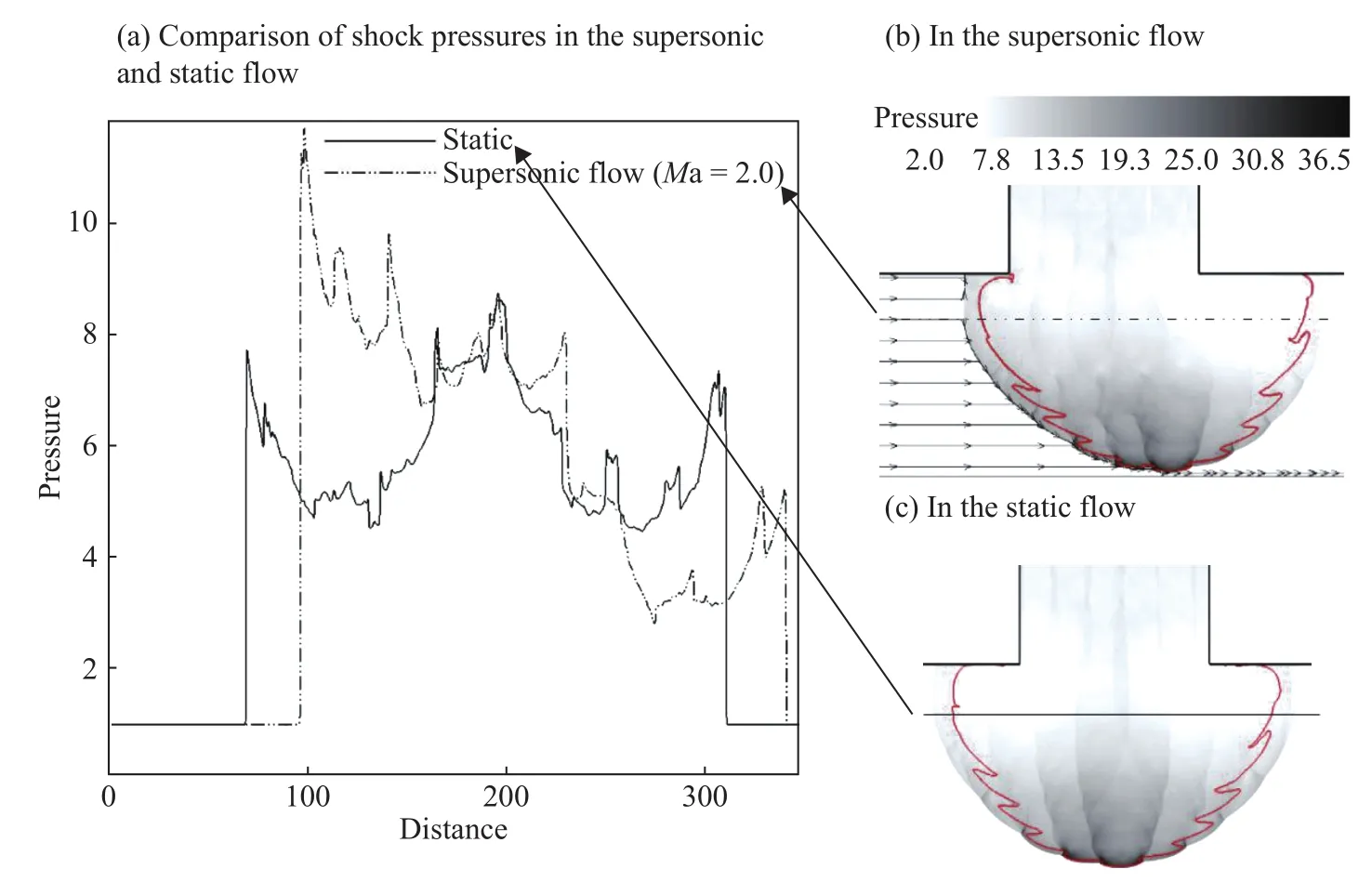
圖9 爆轟波衍射出口處壓力波形比較（紅色細實線近似表示火焰面位置）Fig.9 Comparison of shock pressures in the supersonic (Ma=2.0) and static flow (red line indicates the flame front)

圖9(b)～(c)分別給出了平面爆轟波在超音速和靜止氣流中衍射出口處的壓力波形。超音速氣流加入后，爆轟波在衍射時會向下游偏轉。圖9(a)比較了兩種工況下的壓力分布，可以看出超音速氣流會強烈影響波面的壓力分布，逆流側的激波壓力明顯高于靜止氣流中的激波壓力，相當于在逆流側受到了超音速氣流的壓縮。因此衍射爆轟波在對稱壁面上反射后，反射波的壓力也會維持在一個較高水平，這將極大地促進在反射波后爆轟波的二次起爆。

圖10給出了爆轟波在靜止氣流中的衍射和傳播過程的胞格軌跡。當平面爆轟波從二維管道傳播進入突擴空間時，膨脹波從兩側逐漸侵蝕爆轟波，造成激波與火焰面解耦。而且爆轟波面上的橫波結構由于在兩側失去了可以依靠碰撞而維持其強度的條件，因此其強度逐漸減弱，并且在此過程中留下了較長的軌跡線。而在爆轟波面的中心區域，橫波依然可以依靠其相互之間的碰撞而繼續自持傳播一段距離，直到最終被膨脹波完全削弱，因此胞格分布區域在突擴段出口呈三角形狀，如圖10所示。當爆轟波在對稱面上反射之后，反射波的前導激波強度會大大增強，但是其向前傳播過程中并未產生橫波結構，反而是激波和火焰面逐漸解耦并熄滅，如圖8(a)所示，并不能成功二次起爆。

圖10 爆轟波在靜止氣流中衍射過程的胞格軌跡Fig.10 Cellular structures of detonation diffraction in the static flow

圖11 爆轟波在超音速(Ma=2.0)氣流中衍射和二次起爆過程的胞格軌跡Fig.11 Cellular structures of detonation diffraction in the supersonic flow (Ma=2.0)

前面已經討論過，當來流條件轉變為超音速之后，在逆流側氣流會受到明顯的壓縮作用。相比于靜止氣流中的衍射過程，其激波強度會有所增強，因此與壁面碰撞后的反射波強度也較大，發生二次起爆的幾率也會提高。圖11給出了超音速氣流中爆轟波二次起爆的胞格軌跡。爆轟波衍射后激波和火焰解耦，強度逐漸衰弱，經過對稱壁面反射之后，在反射區域又會重新觸發局部爆轟。但是隨著反射爆轟波逐漸向前傳播，如圖11(b)紅色箭頭所示，在其未與上壁面碰撞之前，其強度是逐漸衰減的。在此過程中激波和火焰面的距離逐漸增大，并且由于不穩定性導致火焰面（即化學反應面）發生褶皺，如圖11(b)所示，之后逐漸發展為波面上的橫波結構，如圖11(a)中紅色圓圈所示。誘導產生的橫波結構不斷地在波面橫向掃略，并與壁面碰撞，在一定程度上增強了激波的強度并促進了爆轟波的二次起爆。關于爆轟波面橫波的產生機制，Jiang等[17]研究了圓柱爆轟波在傳播過程中橫波的產生機制，其中一個重要原因即是化學反應面褶皺，之后逐漸發展形成橫波結構。本文所模擬的工況下，反射波在向前膨脹傳播的過程中，在未與上壁面碰撞之前其傳播的軌跡也類似于圓柱爆轟波，波面在膨脹減弱的過程中由于化學反應面的褶皺，誘導產生新的橫波結構，如圖11(b)所示，這與相關文獻給出的結果吻合。橫波會在一定程度上抑制爆轟波的衰減，并最終誘導爆轟波二次起爆現象的發生。

當超音速來流的強度進一步增強(Ma=4.0)后，爆轟波的二次起爆問題也會得到較大的改善。超音速來流強度越大，在超音速氣流的逆流側激波受到的壓縮作用也越強烈，甚至爆轟波在與下壁面碰撞之前，幾乎不會發生解耦現象。因此在衍射爆轟波與下壁面第一次碰撞后，二次起爆現象便已經成功發生，如圖12所示。此外胞格沿爆轟波傳播方向的長度L（L并非胞格大小，一般胞格大小λ定義為垂直于爆轟波傳播方向的胞格長度）也隨著超音速來流的增強而減小，這是因為爆轟波傳播的絕對速度發生了改變。

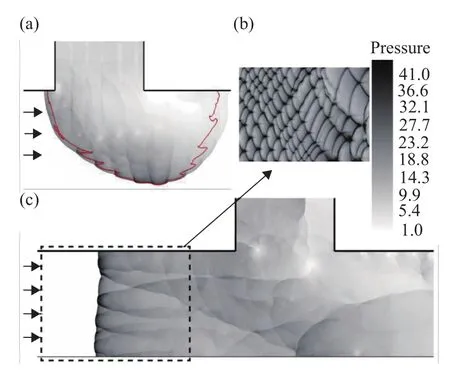
圖12 爆轟波在超音速氣流中(Ma=4.0)的衍射和二次起爆現象Fig.12 Diffraction and re-initiation processes in the supersonic inflow (Ma=4.0)

3 結 論

(1) 對于自發二次起爆過程，加入橫向超音速來流條件的影響后，在核心的三角形流動區域之外產生了更多的橫波結構，并且爆轟波自持傳播的距離隨著來流強度的增加而相應拓展。但是在所研究的幾何尺寸下，爆轟波并未成功二次起爆。在更大尺寸下，超音速來流對爆轟波二次起爆過程的影響還有待進一步研究。

(2) 對于壁面反射二次起爆過程，加入超音速來流條件的影響后，爆轟波的二次起爆過程可有效地被促進。而相同條件下的靜止氣流中，爆轟波將不能成功二次起爆。主要原因是在超音速來流的逆流側，出口氣流由于受到超音速來流的壓縮而壓力升高，所以經過壁面反射后的反射波壓力也較高。反射波在向前傳播的過程中，由于化學反應面的褶皺產生了橫波結構，橫波與壁面和其他橫波相互碰撞增強了前導激波的強度，并最終促進了爆轟波的二次起爆。

本文中初步研究了加入橫向超音速來流對穩定爆轟波衍射和二次起爆過程的影響，但是并未研究橫向超音速來流對非穩定爆轟波（對應不加任何稀釋氣體的可爆混合物中形成的爆轟波）的影響。根據Pintgen[18]的研究結果，非穩定爆轟波和穩定爆轟波在靜止氣流中的衍射過程是完全不一樣的，如其速度衰減過程差別較大。因此，探究橫向超音速來流對非穩定爆轟波衍射過程的影響，并和穩定爆轟波的衍射過程進行對比是必要的，同時其衍射和二次起爆規律也必將與穩定爆轟波不同。因此本文后續的研究工作將探究非穩定爆轟波在橫向超音速來流中的衍射和二次起爆規律。