具有恒定沖擊載荷的梯度泡沫金屬材料設計*

常白雪，鄭志軍，趙 凱，何思淵，虞吉林

（1.中國科學技術大學近代力學系中國科學院材料力學行為和設計重點實驗室，安徽 合肥 230026；2.西安交通大學航天學院機械結構強度與振動國家重點實驗室，陜西 西安 710049；3.東南大學生物科學與醫學工程學院生物電子學國家重點實驗室，江蘇 南京 210096）

多胞材料具有高孔隙率、可變形量大和輕量化特征以及超強的能量吸收能力，廣泛地應用于汽車、航空航天和鐵路等領域。在動態壓縮情形下，多胞材料具有明顯的變形局部化特征和應力增強現象[1-3]，可以很好地提高結構的耐撞性。如何優化設計多胞材料以滿足結構耐撞性要求，是近幾年結構沖擊領域的研究熱點。

多胞材料的準靜態名義應力應變關系呈現明顯的三段式特征：彈性段、長而穩定的平臺段和壓實段。基于此特征，Reid等[1]提出了剛性-塑性-鎖定（R-PP-L）模型，并發展了一維沖擊波模型以表征多胞材料的動態力學行為。Gibson等[4]定量化給出了R-PP-L模型中多胞材料的平臺應力和鎖定應變與相對密度和基體材料屈服應力的關系。該理論已被應用于研究不同相對密度和強度分布下梯度多胞材料的吸能能力和峰值應力[5-10]。然而，R-PP-L模型只滿足對多胞材料力學性能的一階近似，Zheng等[11]提出了更為精確的剛性-塑性硬化（R-PH）模型，其應力應變關系寫作

式中：σ0和C分別為初始壓潰應力和應變硬化參數，這兩個材料參數與多胞材料的相對密度相關[12-13]。Ding等[14]發現基于R-PH模型可以更好地指導爆炸犧牲層的設計。

隨著更為精確的多胞材料本構模型的提出，梯度多胞材料的動態變形機理的研究也趨于完善。但多數研究停留在討論不同梯度多胞材料的動態力學性能上，分析具有不同密度和強度分布的多胞模型的動態力學性能[15-21]。只通過觀察比較其力學響應，選擇滿足耐撞性的要求的梯度模型，無法直接達到最優化的目的。Yang等[13]首次提出了梯度多胞材料的耐撞性反向設計理論，直接設定物體沖擊力要求，反向設計多胞材料的密度分布，并利用三維細觀有限元模擬驗證其有效性。不過，該耐撞性反向設計理論無顯式解，Yang等[13]運用四階龍格庫塔法獲得了數值解。常白雪等[22]利用該理論對二維Voronoi模型進行耐撞性反向設計，并提出了該理論的簡單而方便的漸近解。由于二維隨機蜂窩與三維閉孔胞元的結構差異，針對于二維模型提出的漸近解，無法適用于三維多胞構型的耐撞性設計需求，而對于閉孔多胞構型的耐撞性設計理論的近似解尚未提出。

本文中進一步研究了質量塊以特定的初速度撞擊梯度閉孔泡沫金屬桿的理論模型和有限元模擬：通過討論物體沖擊過程中受載恒定的耐撞性要求，對梯度多胞材料耐撞性反向設計理論進行簡化。針對閉孔泡沫金屬，擬合R-PH模型中初始壓潰應力和應變硬化參數與相對密度的關系；運用級數法，求解耐撞性反向設計理論，獲得梯度多胞材料的密度分布；利用變胞元尺寸法和三維隨機Voronoi技術，生成特定密度分布的梯度閉孔多胞模型；利用有限元軟件ABAQUS/Explicit模塊計算，獲取沖擊力結果驗證設計的有效性，并與均勻密度分布的多胞材料結果進行對比，討論合理的密度分布設計的必要性。

1 理論與方法

1.1 R-PH模型的材料參數

式中：ρ為相對密度，σys為基體材料的屈服應力，k1和k2為擬合參數，分別為1.166和0.115。

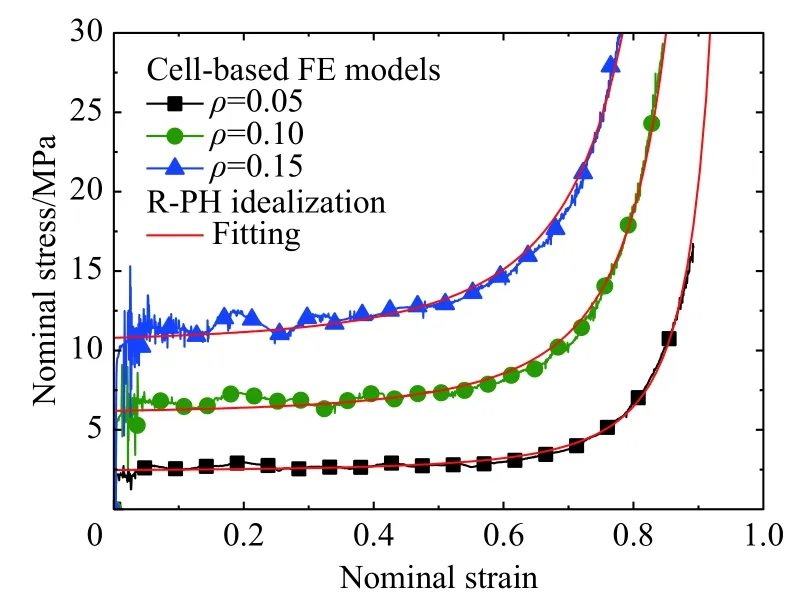
圖1(a) 不同相對密度下閉孔泡沫模型的準靜態應力應變關系Fig.1(a) Nominal stress-strain relations of closed-cell foam models with different relative densities

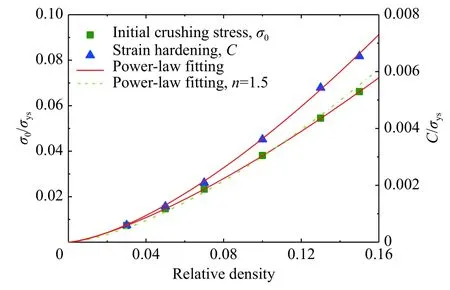
圖1(b) 無量綱初始壓潰應力和應變硬化參數與多胞模型相對密度的冪律關系[13]Fig.1(b) Power-law fitting of material parameters of the R-PH idealization with relative density[13]

1.2 耐撞性設計模型及其漸近解

在質量塊初速度沖擊梯度泡沫金屬材料的過程中，為保護物體安全，且平穩減速，須控制物體在沖擊過程中受沖擊載荷恒定且低于物體耐受載荷。因而，梯度泡沫金屬桿需根據耐撞性要求進行特定的相對密度分布設計。針對二維隨機蜂窩模型的耐撞性反向設計中，常白雪等[22]提出了控制質量塊沖擊梯度多胞金屬桿過程中受載恒定的相對密度分布漸近解，通過二維細觀有限元模擬驗證了設計的有效性，并指出特定的相對密度分布只適用于特定的沖擊情形。對于閉孔梯度泡沫材料，Yang等[13]提出了耐撞性反向設計理論，通過四階龍格庫塔法，針對于控制沖擊過程中質量塊受載恒定、線性遞增和線性遞減的耐撞性要求，獲得了相對密度分布的數值解，但未給出可方便實際工程應用的公式解。本文中針對物體受載恒定的耐撞性要求，對耐撞性反向設計理論進行簡化，運用級數法，求得相對密度分布的漸近解。

考慮一質量為M的物塊以沖擊速度ν0撞擊橫截面面積為A0的閉孔泡沫金屬桿，被保護質量塊在整個沖擊過程中受載恒定，額定受載力為F0。沖擊過程中質量塊的速度為ν=ν0-a0t，其中a0=F0/M為沖擊物體的加速度，t為沖擊時間。沖擊的總時間T0=Mν0/F0，特征長度L0=Mν02/F0。根據Yang等[13]的耐撞性反向設計理論，當沖擊載荷為恒定值時，該理論可以簡化為

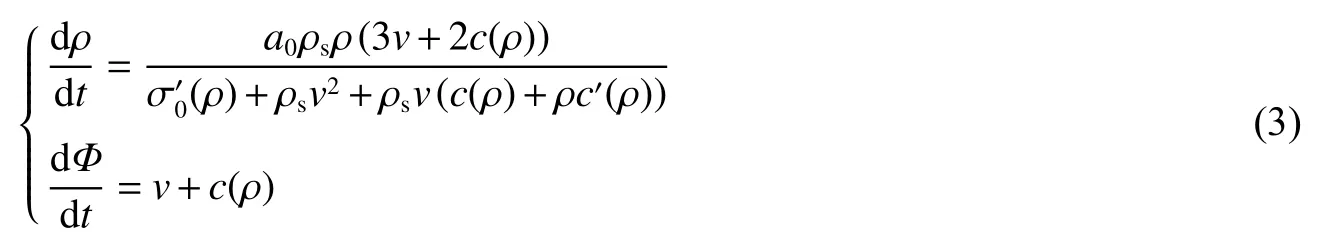
式中：ρ為泡沫金屬材料相對密度，ρs為基體材料密度，Φ為沖擊波陣面位置，撇號表示對ρ的導數，考慮到相對密度、長度、沖擊速度和時間的特征量，定義無量綱量：

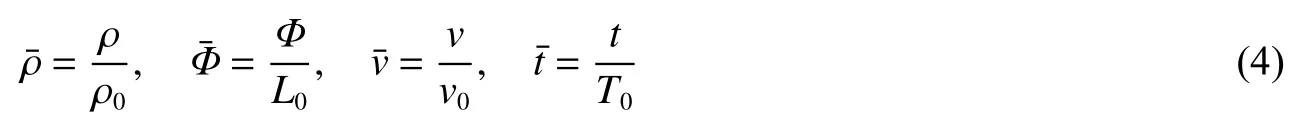
式中：ρ0為沖擊端的相對密度。此時，式(3)可以進一步寫作：

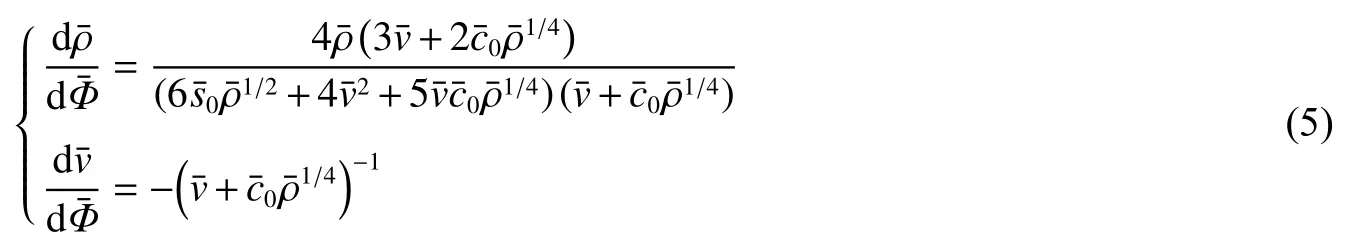
式中利用級數法，可以求得漸近解：

式中：一階系數和二階系數分別為：

和

我們不難得到，在點A和點B的共同作用下，動線段上的點C、D、E均作直線型運動，且可以根據相關的比例關系及A、B的狀態來確定它們的運動速度和方向.

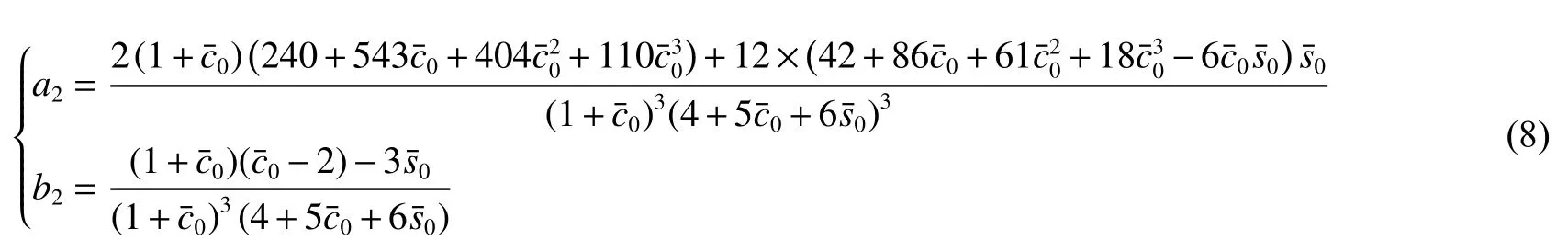
梯度泡沫金屬桿沖擊端的初始相對密度ρ0可以由一維塑性沖擊波模型給出：

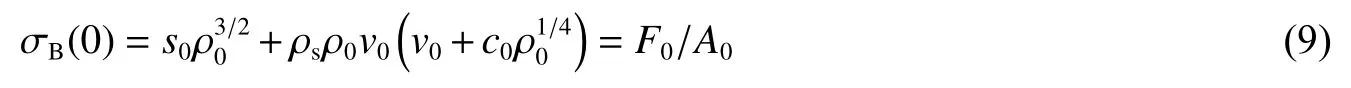
在質量塊沖擊過程中，相對密度單調遞增變化的梯度泡沫金屬桿中塑性壓潰波的傳播滿足一維沖擊波假設，且質量塊隨波后壓實區同步運動，即速度一致[13,22]，波后壓實區應力記為σB。根據應力波理論和牛頓運動定律，如文獻[22]，可以獲得：

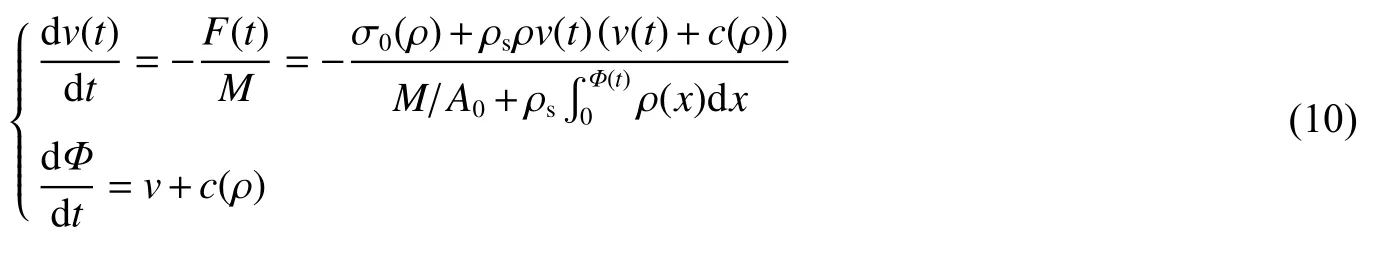
根據漸近求解的相對密度分布和對應的沖擊情形代入上式，可以獲得沖擊力等參量隨時間的變化。

1.3 梯度泡沫金屬材料的數值建模

變胞元尺寸法可用于生成壁厚均一且密度分布連續變化的二維或三維的隨機Voronoi細觀有限元模型[6-7,13]。與基于六角蜂窩構型的二維多胞模型的撒點規則不同，三維多胞結構的撒點規則是基于卡爾文十四面體提出的。Yang等[13]基于均勻三維Voronoi結構引入了新的撒點規則，在一定區域內隨機撒點，通過已知的相對密度分布和壁厚，控制任意兩個相鄰成核點i和j之間的間距不小于當前位置的最小許可間距，記為

式中：h為胞元胞壁厚度，k為胞元不規則度，ρ（xij，yij，zij）為i和j兩核點連線中點位置對應的相對密度。本文中只考慮x方向上的相對密度分布，xij=（xi+xj）/2，其他兩個方向相對密度均勻分布。

梯度泡沫金屬的基體材料模型和參數與文獻[13]一致。基體材料假設為彈性-理想塑性，其密度ρs=2 700 kg/m3，楊氏模量Es=69 GPa，泊松比ν=0.3，屈服應力σys=165 MPa。采用殼單元S3R劃分胞壁網格，通過網格收斂性分析[11]，其殼單元的特征尺寸大小為約0.3 mm。梯度泡沫材料細觀有限元模型的橫截面為正方形，其面積A0=30×30 mm2。模型中所有可能的接觸設置為摩擦因數為0.02的通用接觸，沖擊加載示例見圖2。

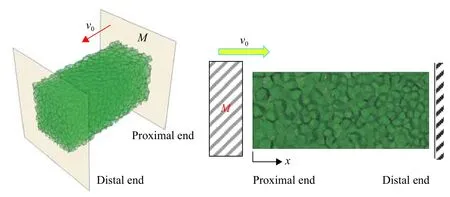
圖2 質量塊沖擊梯度多胞桿Fig.2 A diagram of 3D graded Voronoi models under mass impact

2 結果與討論

2.1 梯度泡沫金屬材料相對密度分布的設計

上文已經給出了恒定沖擊力耐撞性反向設計理論的一階和二階近似解，本文中采用與Yang等[13]沖擊情形一致：沖擊物體質量M=50 g，初始沖擊速度ν0=100 m/s，額定受力為F0=7.5 kN。由此可得，特征時間T0=66.7 ms，特征長度L0=66.7 mm。沖擊端相對密度為0.086 9。參數則有漸近解中的系數為a1=0.570和a2=0.191。

通過已獲得的上述參數表征相對密度分布，并與Yang等[13]的結果進行比較驗證。根據初始壓潰應力與相對密度的關系，獲得相對密度梯度分布的漸近解，將Yang等[13]的數值結果作為精確解進行對比，如圖3(a)所示。漸近解與精確解在沖擊端的相對密度有小量差距。漸近解的結果0.086 9與精確解的結果0.085 0相比，相對誤差約為2%，可以忽略。比較漸近解與精確解給出的相對密度分布表明，一階近似解只是線性近似，沖擊端附近差異較小，越靠近遠端與精確解差異越大；二階近似解的整體差異相比較小，沖擊端附近稍大于精確解，遠端附近稍小于精確解。

結合應力波理論和牛頓第二運動定律，理論預測特定密度分布的梯度泡沫金屬材料的力學行為。將相對密度分布和特定沖擊情形代入公式進行理論預測，運用四階龍格庫塔法求解，可以獲得沖擊力、速度和波陣面位置隨時間的演化過程。通過觀察沖擊力隨時間的演化過程，二階近似和精確解模型的結果與耐撞性額定沖擊力值非常吻合，而一階近似模型結果初期吻合較好，后期差別較大，如圖3(b)所示。通過沖擊速度降為0時確定波陣面傳播停止的位置，獲得梯度泡沫金屬桿的長度分別為：69.4 mm（一階近似模型）和65.9 mm（二階近似模型）。精確解給出的梯度泡沫金屬桿的長度為66.3 mm，如圖4(b)所示。通過理論預測，二階近似解具有足夠的精度，可用于設計具有恒定沖擊載荷的梯度泡沫金屬材料細觀有限元模型的相對密度分布。

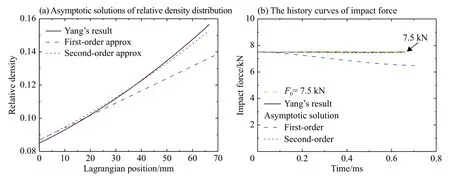
圖3 相對密度分布的漸近解和沖擊載荷歷程的理論預測值Fig.3 Theoretical predictions of asymptotic solutions of relative density distribution and the history curves of impact force

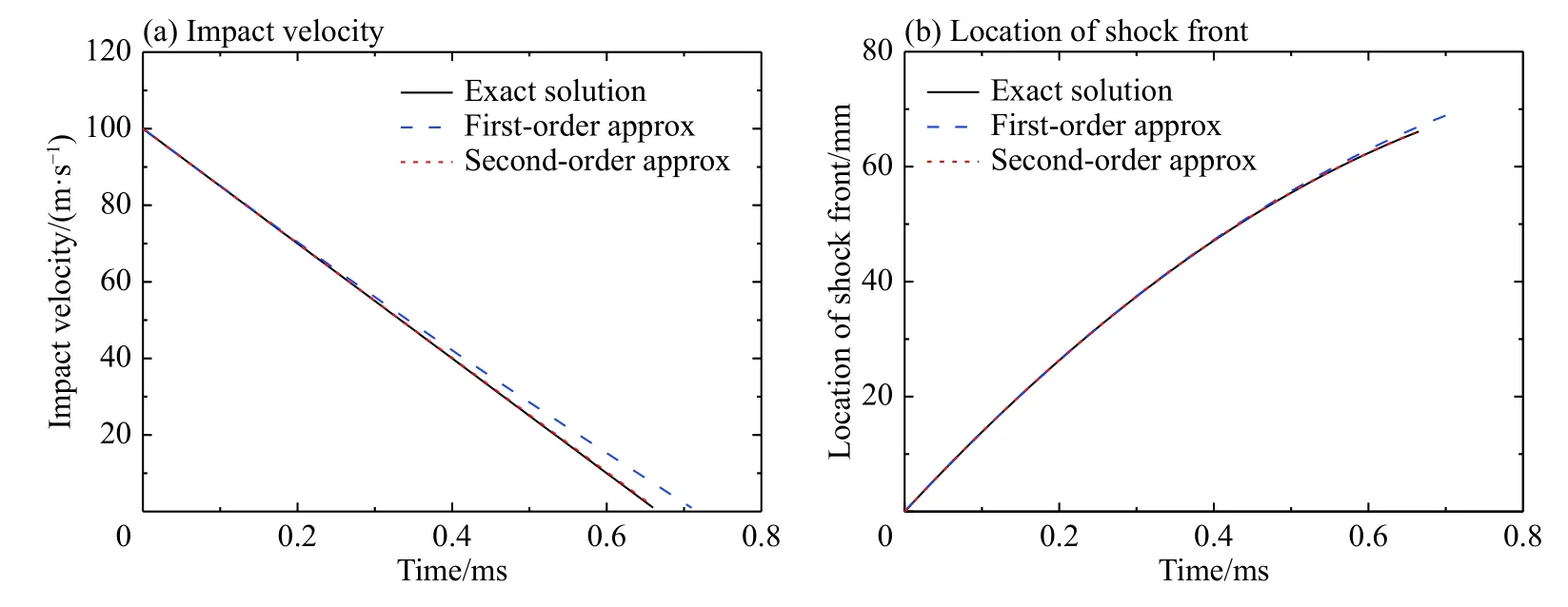
圖4 沖擊速度與沖擊波波陣面位置的歷史曲線Fig.4 Evolution history of impact velocity and location of shock front

2.2 有限元模擬結果

基于已獲得的相對密度梯度分布，利用變胞元尺寸法，生成梯度泡沫金屬桿的細觀有限元模型，并生成均勻密度分布的泡沫金屬細觀有限元模型作對比。均勻密度模型與二階近似密度梯度模型的整體尺寸一致，平均相對密度一致，相對密度為0.117，三維Voronoi模型如圖5所示。取中軸面x=15mm處剖面圖觀察其變形過程，可以發現一階近似和二階近似模型在剛性板的沖擊過程中，以逐層壓潰變形模式為主，在密度較小端胞元開始發生壓潰，并形成一道較為穩定的塑性沖擊波向遠端傳播，如圖6(a)～(b)。而對于均勻密度分布的細觀有限元模型，其撞擊初始變形以沖擊端胞元壓潰為主，形成一道向遠端傳播的沖擊波。隨著剛性板的繼續推進，由于端部效應，桿內應力波在固支端反射加強，其應力超過了支撐端部分胞元的初始壓潰應力，隨即發生壓潰變形。由于沖擊情形為質量塊初速度撞擊，沖擊能量有限，端部反射波只能使得少量胞元發生壓潰，并不能使得該壓潰波傳播很遠，最終壓潰帶寬度約為3～4個胞元直徑，如圖6(c)。比較密度均勻和梯度分布多胞模型變形圖，發現合理地設計相對密度分布，可以有效地控制壓潰波的形成和傳播。

圖5 密度梯度多胞桿細觀有限元模型Fig.5 Cell-based finite element models of density gradient cellular rods

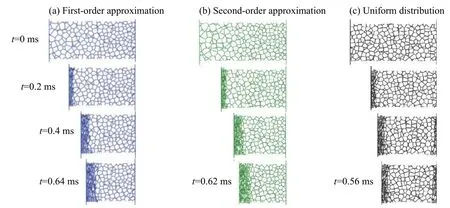
圖6 梯度多胞細觀有限元模型中軸剖面變形圖Fig.6 Deformation patterns of cell-based finite element models in the middle section of the density gradient cellular rods perpendicular to x-axis

梯度泡沫金屬桿沖擊端發生局部化壓潰，產生塑性沖擊波向遠端傳播。波前未壓實區應力和速度分別為為σ0和0，其中初始壓潰應力為σ0(ρ(Φ(t)))=s0ρ3/2，即當前t時刻波陣面位置處對應的初始壓潰應力，則支撐端力Fsup=A0σ0。有限元計算的支撐端和沖擊端力的結果與相對密度分布精確解模型的理論預測結果比較見圖7。有限元計算的結果出現震蕩，其原因為：剛性板初始接觸階段，試件和剛性板間的罰函數接觸算法會導致震蕩；后期頻率較高的震蕩為胞壁內部的彈性波來回傳播及交互作用導致的；后期低頻且幅值較大的震蕩是由于胞元的失穩壓潰產生的。一階近似下的有限元模型的計算結果與理論預測值比較：初始階段有限元計算的沖擊力結果偏高于額定沖擊力，后逐漸趨于額定值并重合；有限元計算的支撐端力結果與理論預測結果初期呈遞增趨勢，初始階段有限元計算的結果高于理論預測值，上升斜率較小，后逐漸低于理論預測值，整體相比差異明顯。二階近似下的有限元模型的計算結果與理論預測值比較表明，沖擊力結果整體維持較為穩定的狀態，在某一恒定值附近震蕩，其值稍大于額定設計值；支撐端力結果與理論預測值初期都呈現遞增趨勢，初始階段有限元計算結果稍高于理論預測值，后逐漸趨于理論預測值，整體偏高。二階近似模型相比于一階近似模型可以很好地控制沖擊力在某一恒定值附近震蕩，其值偏高于額定值，與Yang等[13]的結果基本一致，如圖8(a)所示。這表明二階近似解可以很好地表征精確解，而一階近似解的精度不夠。初始壓潰應力與相對密度3/2次冪的關系可以應用于指導梯度泡沫材料的耐撞性設計。

與二階近似模型結果對比，均勻密度分布的泡沫金屬模型的沖擊力結果具有明顯的峰值且高于額定載荷，后隨時間衰減。由于沖擊初期，質量塊沖擊速度最高，沖擊端相對密度（0.117）大于二階近似模型（0.086 9），其初始壓潰應力和應變硬化參數較高，使得初期沖擊力明顯高于二階近似模型，如圖8(a)所示。隨沖擊速度的降低，其對應的沖擊力也相應減小，出現明顯的沖擊力峰值后衰減，而二階近似模型相對密度單調遞增，補償了因速度衰減對沖擊力的影響，很好地控制了沖擊力的穩定演化。觀察物體沖擊速度隨時間的衰減過程發現，有限元模擬結果要比理論預測衰減偏快，用時稍短。以沖擊速度降為0時表征沖擊結束，一階和二階近似模型實際沖擊時間分別為0.64 ms和0.62 ms，而均勻密度分布模型速度衰減得最快且不穩定，沖擊時間為0.56 ms，耗時最短，如圖8(b)所示。合理地優化梯度泡沫金屬材料相對密度的分布，對于控制質量塊沖擊力是必要的。

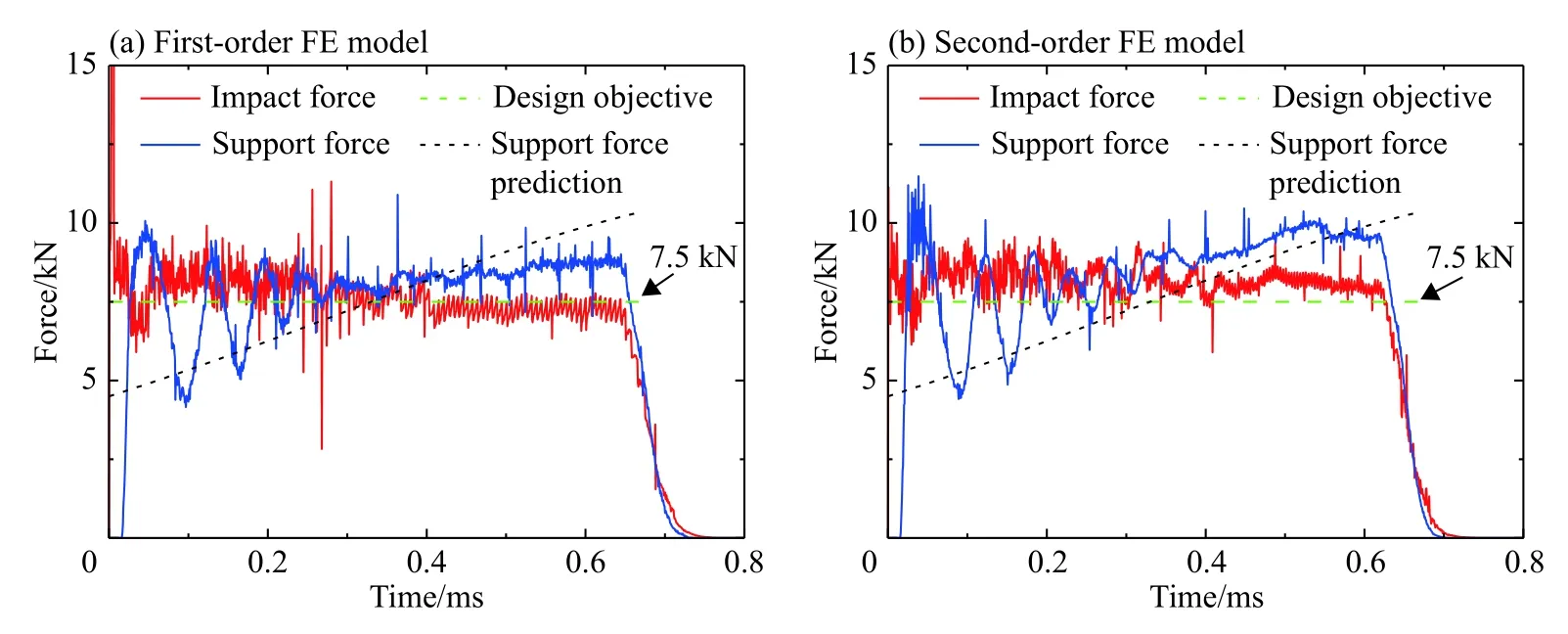
圖7 沖擊端和支撐端載荷理論預測與有限元計算結果的比較Fig.7 Comparisons of impact force and support force curves history between theoretical predictions and finite element (FE) results

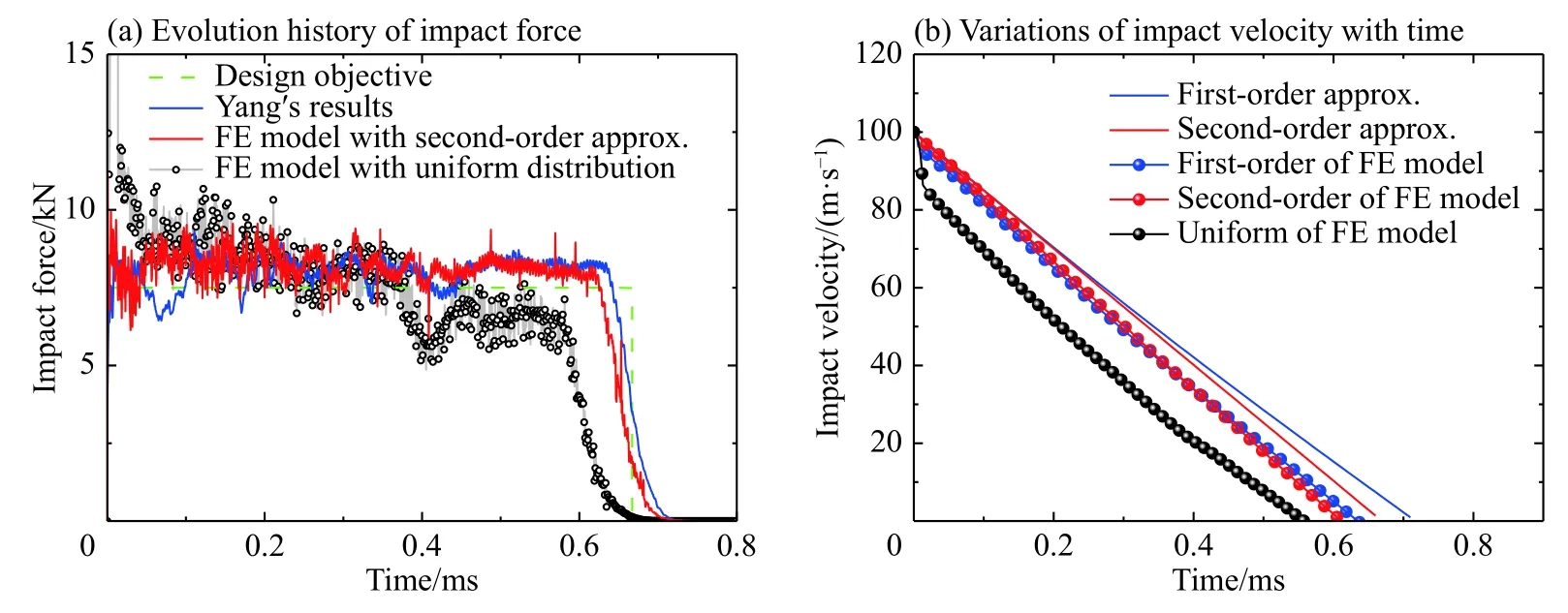
圖8 有限元計算結果對比Fig.8 Comparisons of finite element (FE) results

圖7和圖8中有限元模擬的結果偏高于理論預測值，可能原因是本文中采用的沖擊波模型未考慮多胞材料的率敏感性影響，初始壓潰應力和應變硬化參數均使用準靜態應力應變關系擬合得到，導致理論值低估有限元模擬的結果。已有研究表明，即使在未考慮基體材料應變率效應的影響下，多胞材料的動態應力應變關系與準靜態的應力應變關系有明顯的不同。Zheng等[11]發現了泡沫金屬一種特有的率敏感性——“沖擊速率敏感性”，即多胞材料動態壓實區的應力應變狀態對應于特定的沖擊速度，不同沖擊速度下的狀態點可以用一條曲線描述，該曲線可用于表征多胞材料動態下的應力應變關系。通過比較動態應力應變關系和準靜態的應力應變關系發現，動態初始壓潰應力高于準靜態初始壓潰應力，而動態應變硬化參數小于準靜態應變硬化參數。Ding等[23]和Wang等[24]進一步研究發現了泡沫金屬的初始壓潰應力具有應變率敏感性，在應變率高到一定程度后二者有冪率關系。因而，后期研究中可以考慮泡沫金屬材料率敏感性的影響，以提高設計的準確度。在實驗研究方面，He等[25]提出了通過控制水冷前發泡時間可以制備連續密度梯度變化的閉孔泡沫金屬，將有助于后期耐撞性反向設計理論的實驗驗證。

3 結 論

本文中基于一維率無關剛性-塑性硬化（R-PH）模型，獲得了泡沫金屬的初始壓潰應力和應變硬化參數與相對密度呈3/2次冪的關系。針對于恒定沖擊力的耐撞性要求，對梯度泡沫金屬的耐撞性反向設計理論進行簡化，運用級數法，獲得了閉孔梯度泡沫金屬材料相對密度分布的漸近解，與Yang等[13]的精確解進行了比較。通過理論結果的比較發現：兩者初始相對密度具有微小差異，但可以忽略；一階近似解是對精確解的線性近似，誤差較大；二階近似與精確解吻合較好。通過沖擊力理論預測判斷，二階近似密度分布可以達到恒定沖擊力要求，而一階近似結果在后期無法確保沖擊力維持恒值。根據相對密度分布的漸近解，設計三維梯度細觀有限元模型并進行計算驗證。通過與數值模擬結果的比較發現：二階近似模型沖擊力一直維持較為穩定的恒定沖擊力，很好地滿足了恒定沖擊載荷的耐撞性要求；一階近似模型沖擊力無法維持較為穩定的載荷；均勻密度分布的多胞模型沖擊力具有明顯的峰值，后隨時間衰減。相比均勻密度多胞材料，單調遞增的二階近似密度梯度設計，合理地分配密度的強弱，控制載荷穩定演化，使得速度平穩降低，提高了撞擊過程物體的穩定性。綜上所述，耐撞性反向設計理論簡化模型的漸近解對于梯度閉孔泡沫材料的耐撞性設計是有效的，所提出的耐撞性設計方法在控制沖擊吸能過程和沖擊物受載方面具有指導意義。