高等代數課程中抽象思維及方法論教學探討

夏春光

摘要：高等代數課程注重抽象思維的訓練，同時也注重數學方法的運用。本文以特定內容探討抽象思維與數學方法在高等代數課程中的教學。具體而言，一方面以一些代數基本概念的漸次演變來探討抽象思維的教學，另一方面，以化二次型為標準形的幾種典型與非典型方法來探討數學方法的教學。

關鍵詞：高等代數;抽象思維;方法論

doi：10.16083/j.cnki.1671-1580.2019.05.023

中圖分類號：G642 文獻標識碼：A 文章編號：1671-1580（2019）05-0095-04

一、前言

高等代數是高等院校本科數學專業最重要的基礎課程之一。該課程在國內大多數教材中通常包含以下主要教學單元：多項式理論，行列式理論，線性方程組理論，矩陣理論，二次型理論，線性空間理論，線性變換理論，歐式空間理論以及若當標準型理論及雙線性代數理論。大多數教材都是穿插安排數學方法與計算及代數概念的抽象及邏輯思維訓練。在席南華院士著的教材《基礎代數》中，講解的內容更加系統和深入，該教材第一卷側重數學方法與計算，第一卷的第五章及第二卷側重代數概念的抽象及邏輯思維訓練。

在高等代數主要教學單元中，有的側重抽象思維及邏輯思維訓練，比如：多項式理論中的基礎概念引入部分蘊含著域、環、群的漸次抽象，線性方程組理論中線性組合、線性表示、線性相關、線性無關等核心概念的敘述，線性空間理論中線性空間概念八條公理的結構性展示，歐式空間中歐式空間概念四條公理的幾何化引入。本文將以域、環、群的漸次抽象演變來探討高等代數課程中代數概念的抽象思維的教學。

高等代數課程教學還強調數學方法與計算。比如：多項式理論中帶余除法及輾轉相除法的計算，行列式計算中常用計算方法及特殊行列式的計算技巧，二次型理論中化二次型為標準形的三種典型方法，線性變換理論與矩陣理論中線性變換與矩陣的對應關系。大多數教材都包括化二次型為標準形的三種典型方法：配方法、合同變換法、正交相似對角化法。此外，還有一些非典型方法，比如雅克比法、偏導數法等。本文還將以高等代數課程中化二次型為標準形的典型與非典型方法來探討數學方法的教學。

二、抽象思維的教學探討

本節將以域、環、群的漸次抽象演變來探討高等代數課程中代數概念的抽象思維的教學。在多項式理論引入基礎概念時蘊含著域、環、群的漸次抽象。在席南華院士所著的教材《基礎代數》第一卷中，專門有第五章進行了講解。

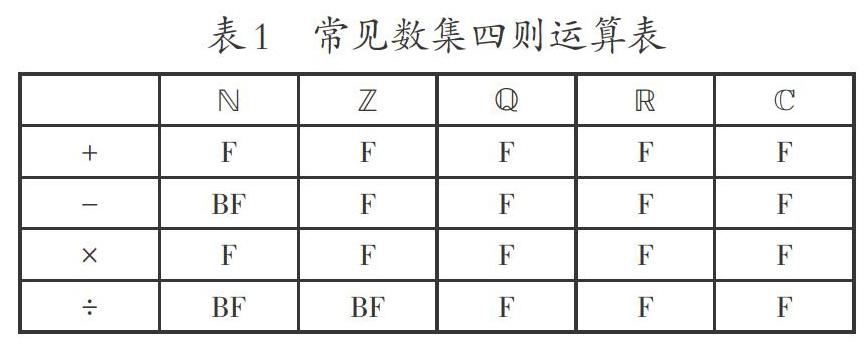
（一）常見數集四則運算表

以下我們用字母N、Z、Q、R、C分別表示中學階段學過的自然數集（含數字O）、整數集、有理數集、實數集、復數集。考慮這些集合對四則運算的封閉性，用符號F及BF分別表示四則運算的封閉與否，很容易得出表1。

（二）第一次抽象

觀察上述表格，關注數集對四則運算的封閉性。可以看出，有理數集、實數集、復數集對于加、減、乘、除均是封閉的，并且在這三個數集中都含有數字0和1。由此，給大一新生講解數域概念時，可以自然地稱滿足這樣特點的數集就為“數域”。同樣地，可以看出整數集除了除法運算都是封閉的，并且也含有數字0和1，可以自然地稱滿足這樣特點的數集就為“數環”。這樣就容易讓學生從中學熟悉的知識過渡到大學知識。這也讓學生們更容易理解，為什么在高中時就經常聽老師說有理數域、實數域、復數域了，原因是它們確實是數域。當然，進行概念的抽象時，我們還應關注新的概念是否包含非平凡的例子。事實上，我們可以構造如下的集合。

從數域的定義，我們知道復數域是最大的數域，且容易證明有理數域是最小的數域，而實數域是介于有理數域與復數域之間的常見數域。上述例1就是一個介于有理數域與復數域之間的且不同于實數域的非平凡的例子，常稱為高斯數域。同樣道理，上述例2是一個不同于整數環的例子，常稱為高斯整環。

（三）第二次抽象

在第一次抽象的基礎上，關注運算律及特殊元的存在性。我們注意到，數域有兩種運算，一種是加法“+”，另一種是乘法“×”，加法滿足結合律，交換律、含有數字0，每個數相對于加法存在負數，乘法滿足結合律、交換律，含有數字1，每個非零數相對于乘法存在倒數，此外，乘法對加法滿足分配律。將上述特點抽象出來就可以給出下述一般域的定義，去掉了“數”這個定語。

上述例3是最簡單而又最重要的有限Galois域，其在密碼編碼學中具有重要的應用。日常生活中也常見其身影，比如計算機處理數據使用的二進制，還比如全世界都在使用的星期計時用的七進制。上述例4是高等代數教學中需要重點講解的，在整個高等代數理論中起著重要作用的數學工具。

（四）第三次抽象

在第二次抽象的基礎上，關注運算名稱，我們注意到域的兩種運算均滿足相同的運算律，均含有平行的特殊元（如加法零元與乘法幺元，加法負元與乘法逆元）。將這些共性抽象出來就可以得到群的概念：群含有一種運算，常稱為乘法“·”，此運算封閉，且滿足結合律，含有單位元，每個元都有逆元。進一步，如果要求群運算滿足交換律就稱為交換群，即Abel群。另外，如果不要求逆元的存在性，就抽象出了半群的定義。在這一層次，我們可觀察下面的例子。

上述例5稱為4階二面體群，其可看成保持正方形不變的2個旋轉（順時針旋轉90度，逆時針旋轉90度）和2個反射（上下反射，左右反射）所組成的非交換群。上述例6是最簡單的半群，也就是說，從幼兒園時期，老師家長就在口口相傳的1加1等于2這些口訣，實際上是最基本的代數單元：半群。

（五）抽象思維的教學注意點

從上述三次具體的抽象過程可以看出，教師在實際教學過程中，對于抽象概念的講解引入應當注重：1.由淺入深，由學生熟悉的知識逐漸過渡到新的概念;2.抽象過程應當引導學生在一定程度上抓住原始概念某些方面的本質，并賦予“新的”具有代表性的名稱;3.抽象過程應當是真正意義上的抽象，而不能僅僅是換個名稱，應當舉出實例讓學生明白，這一過程確實進行了抽象，確實包含了原始概念不能覆蓋的情形，從而將多個概念放到一個更大的框架下進行認識，提升學生的認識問題的深度。