一類具有B-D發生率的隨機SIQS模型的動力學行為研究*

胡晶晶韋煜明彭華勤

(廣西師范大學 數學與統計學院，廣西 桂林 541004)

0 引言

傳染病作為一種常見病和多發病，是世界上造成死亡的第二大原因，所以傳染病的預防和控制就尤為重要，為了減少易感人群被感染的風險，隔離感染者是一種有效控制疾病傳播的方法.自Kermack和Mc Kendrick[1]提出SIR倉室模型以來，大量的數學模型被建立并用來描述傳染病動力學，[2-6]幫助制定有效的措施來控制傳染病的傳播，所以數學模型在流行病學研究中發揮著重要作用.近些年來各種流行病模型的提出和廣泛探索，使得疾病防治研究取得了很大進展.魏等人[7]提出了一個具有校正隔離率的SIQS模型：

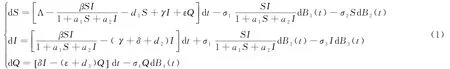
其中，S(t)為易感者在t時刻的人口數量，I(t)為t時刻染病者的人口數量，Q(t)為在t時刻已接受隔離的人口數量，參數Λ，d1，d2，d3，為正常數，δ，ε，γ，a1，a2為非負常數，Λ為人口輸入率，β為易感者與染病者的接觸率，d1為易感者的自然死亡率，d2為感染者由疾病引起的死亡率，d3是隔離者由疾病引起的死亡率，δ為感染者的隔離率，γ，ε分別是感染者與隔離者重新回到易感者的比率，表示的是不含隔離者，且依賴易感者和感染者的校正隔離率，B i(i=1，2，3，4)是獨立的布朗運動，代表白噪音的強度.魏等人討論了解沿無病平衡點滅絕的充分條件以及正解的平穩分布.Cao等人[8]研究了帶有quarantine-adjusted發病率的SIQR傳染病模型，此時接觸率為，并對接觸率和種群白噪音擾動，得到了疾病滅絕與遍歷分布的充分條件.基于以上學者的研究，本文討論了帶有Beddington-DeAngelis發生率的SIQS傳染病模型，對接觸率β白噪音擾動，即，并假設隨機擾動對每個種群是線性擾動，因此得到如下模型：

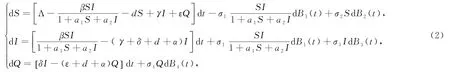
d是自然死亡率，α是因病死亡率，且，其他參數含義與模型(1)相同.

本文通過構造合適的Lyapunov函數，利用It?公式，鞅的強大數定理等相關的隨機微分方程的知識，討論在一定條件下隨機SIQS系統(2)的消亡與存在遍歷性平穩分布問題.

1 全局正解的存在唯一性

1.1 預備知識

令(Ω，F，{F}t≥0，P)是完備概率空間，函數B i(t)(i=1，2，3，4)是定義在完備概率空間上的標準布朗運動，令X(t)是d-維的Ito過程，則

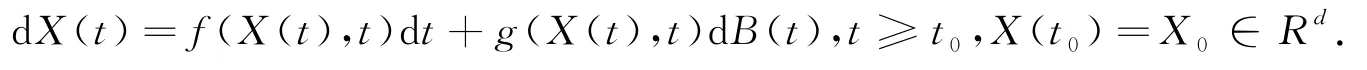
令V∈C2，1(R d×[t，∞];R+)，則V(X，t)也是It?過程且定義如下：

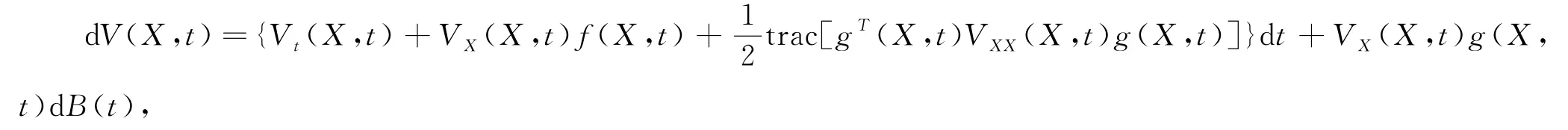
對于系統(2)這樣一個隨機微分方程，我們首先考慮其解的存在唯一性.

1.2 全局正解的存在唯一性

定理1對任意初值，系統(2)存在唯一的全局正解(S(t)，I(t)，Q(t))，并且該解依概率1位于中，即.

證明：因為系統(2)的系數滿足局部Lipschitz條件，不滿足線性增長條件，則對任意初值，系統(2)在[0，τe)上存在唯一的局部解，τe為爆破時刻.為了證明解是全局的，我們只需證τe=∞.a.s.設η0＞0且滿足S(0)＞η0，I(0)＞η0，Q(0)＞η0，對任意η≤η0，定義停時列：

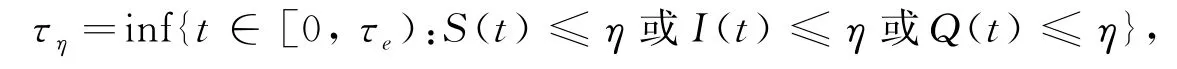
記infΦ=∞(Φ表示空集).由停時的定義知，當η→0時，τη單調遞增.令，顯然τ0≤τe，若能證得τ0=∞.a.s.則τe=∞.a.s.故只需證明τ0=∞.a.s.現用反證法證明，如果τ0＜∞，則存在T＞0和ζ∈(0，1)，使得P(τ0≤T)＞ζ，因此存在一個正整數η1∈(0，η0)使得當η∈(0，η1)時，

定義一個C2函數：

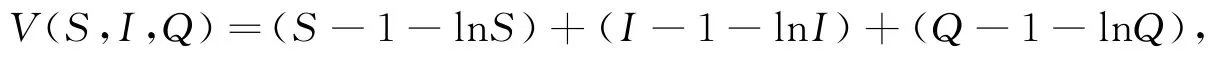
根據It?公式可得

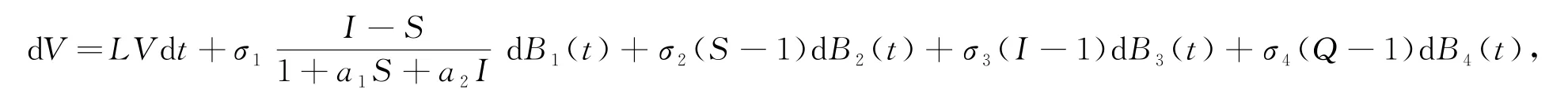
其中

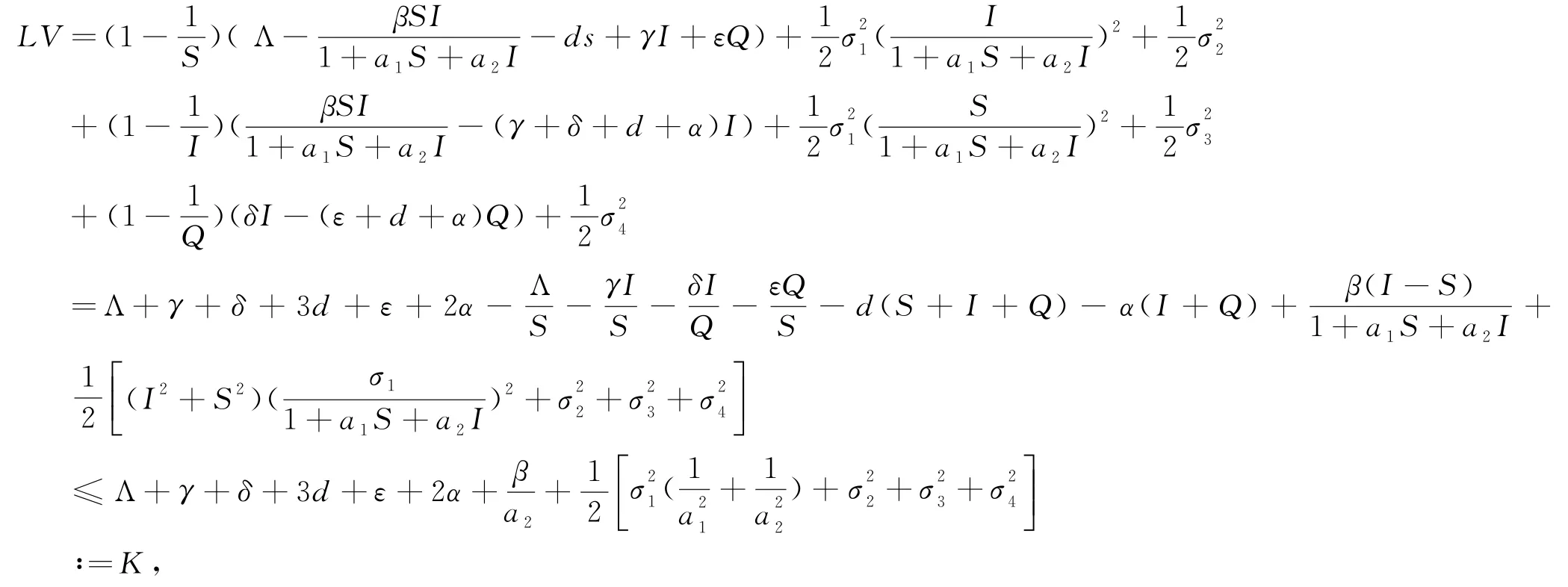
因此，

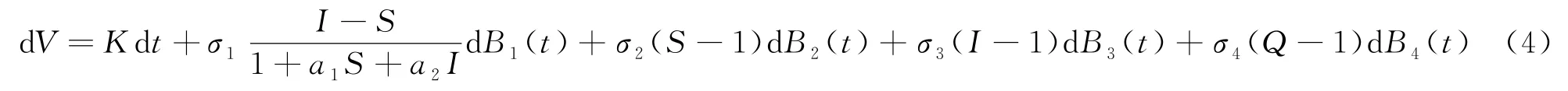
對(4)式兩邊同時從0到τη∧T積分，有

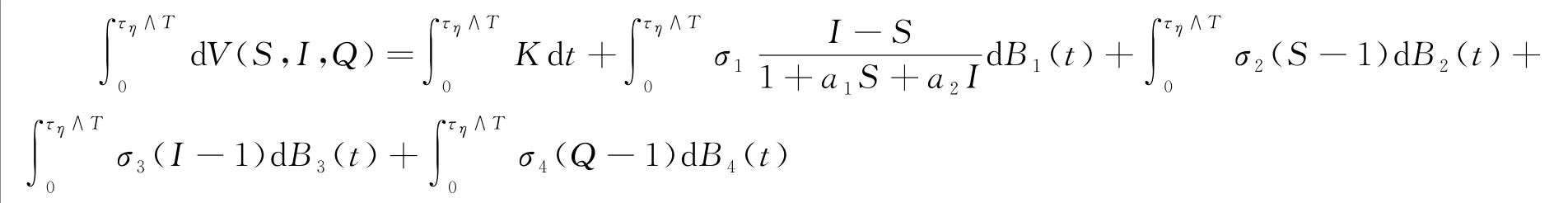
對上式取期望，則有

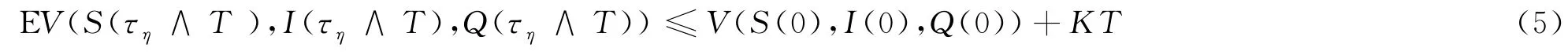
設Ωη={τη≤T}，則P(Ωη)≥ζ，對每個ω∈Ωη，由停時的定義可知，在S(τη，ω)，I(τη，ω)，Q(τη，ω)中至少有一個等于η，所以

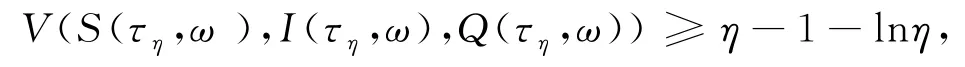
由(5)可知，

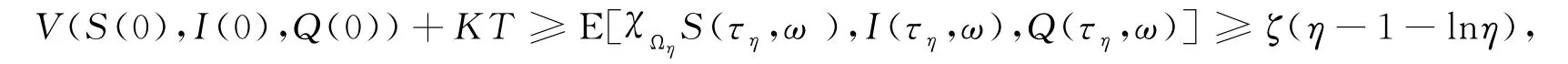
所以τ0=∞.a.s.即系統(2)存在全局唯一正解.

2 遍歷平穩分布

定義閾值為：

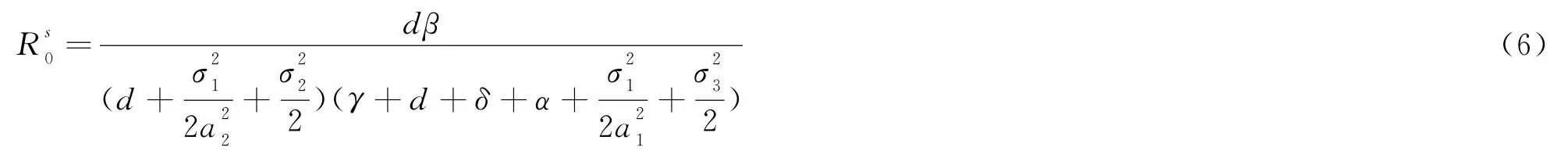
定理2令(S(t)，I(t)，Q(t))是系統(2)關于初值的解，如果

疾病存在遍歷性平穩分布，即疾病持久.

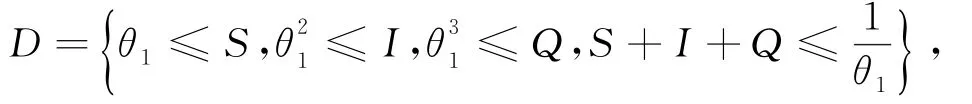
這里θ1是足夠小的正常數.在集合選擇足夠小的θ1滿足下面的條件：

這里M＞0，F是正常數，且滿足

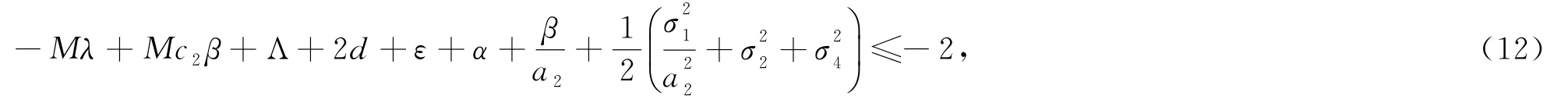
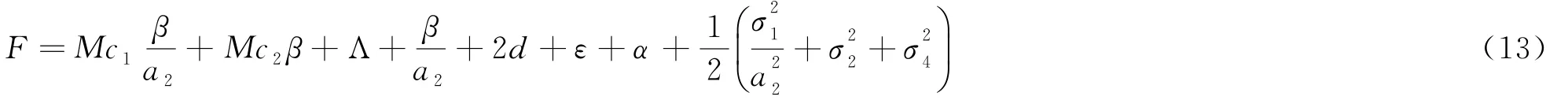
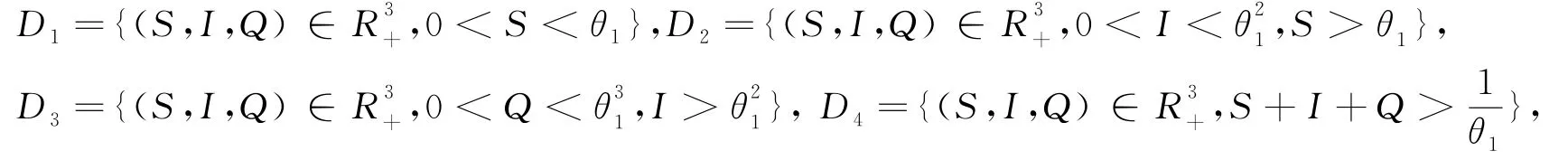
首先給出系統(2)的擴散矩陣：

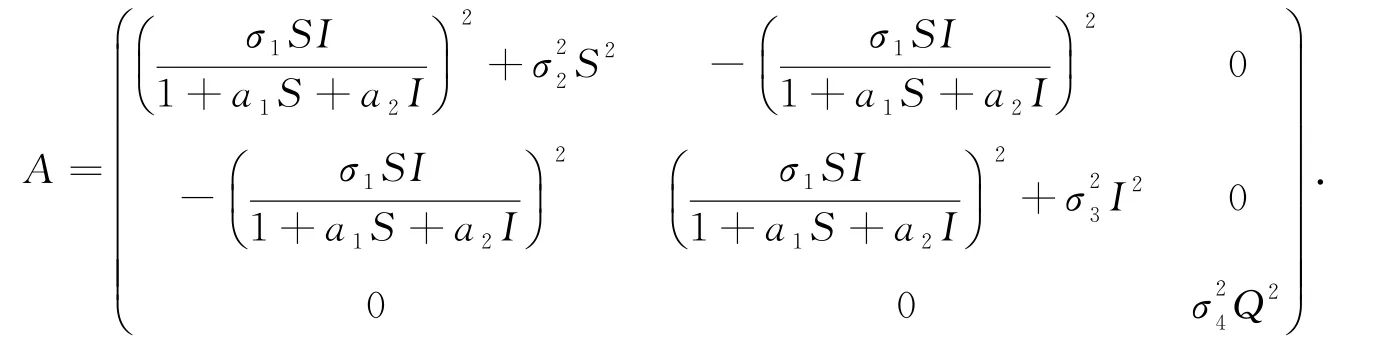
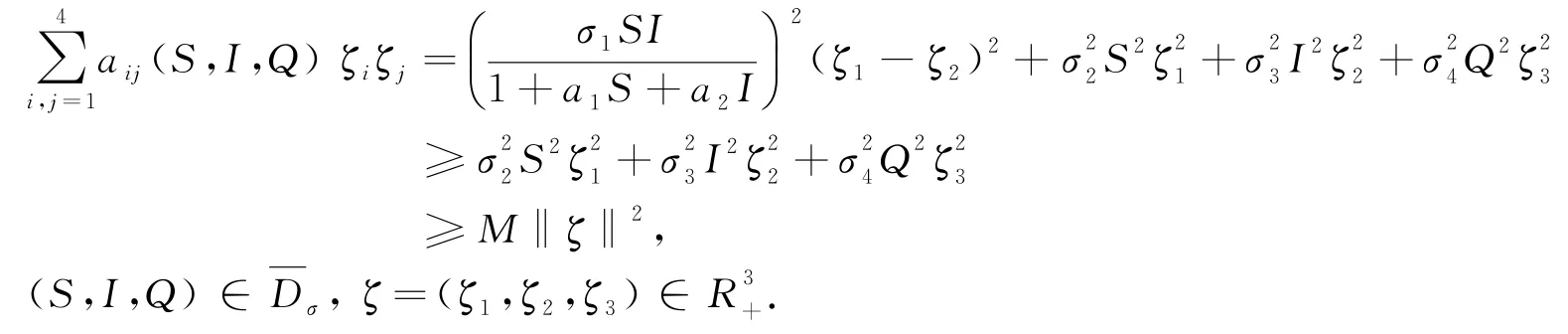
由系統(2)和It?公式可知，

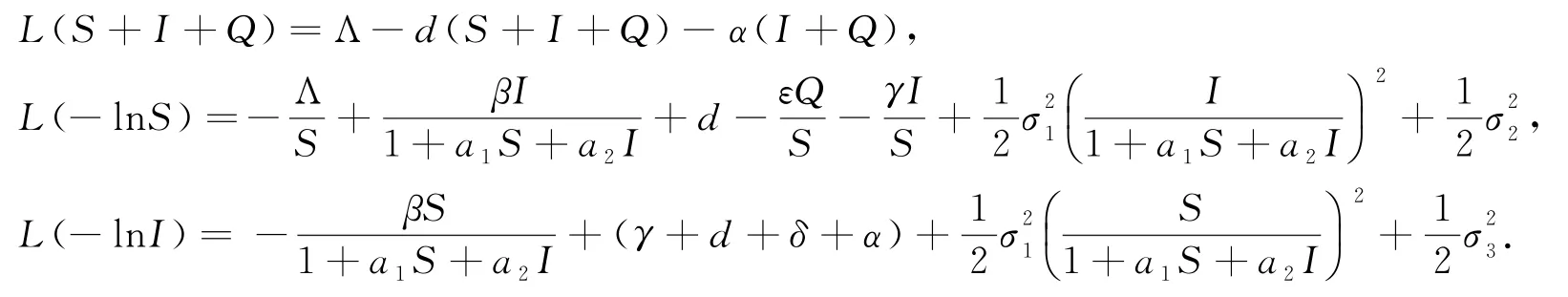
定義C2函數，

這里c1，c2是正常數，根據公式It?可知

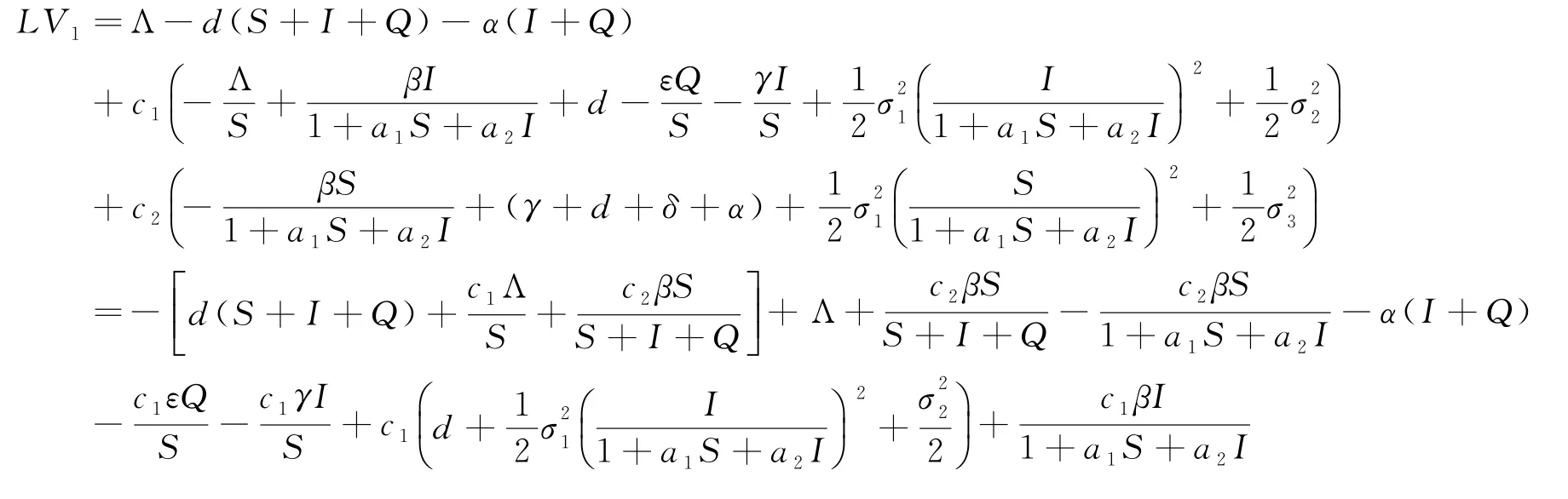
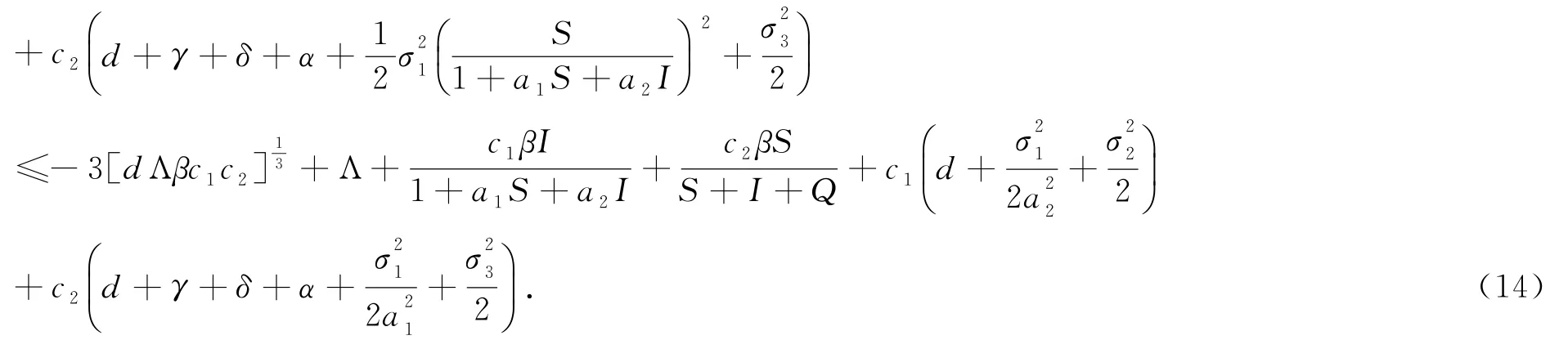
即(14)式可寫成

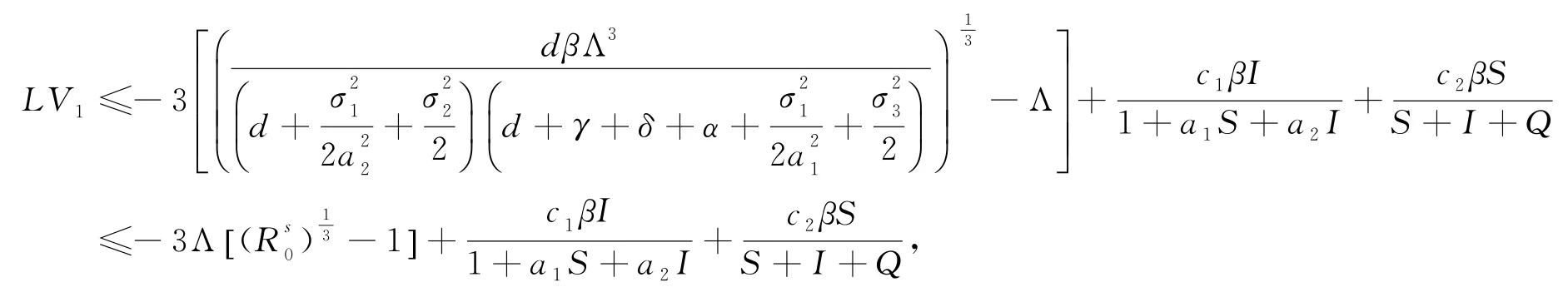
且M滿足(12)式，則有，

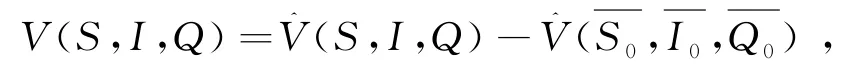
因此，

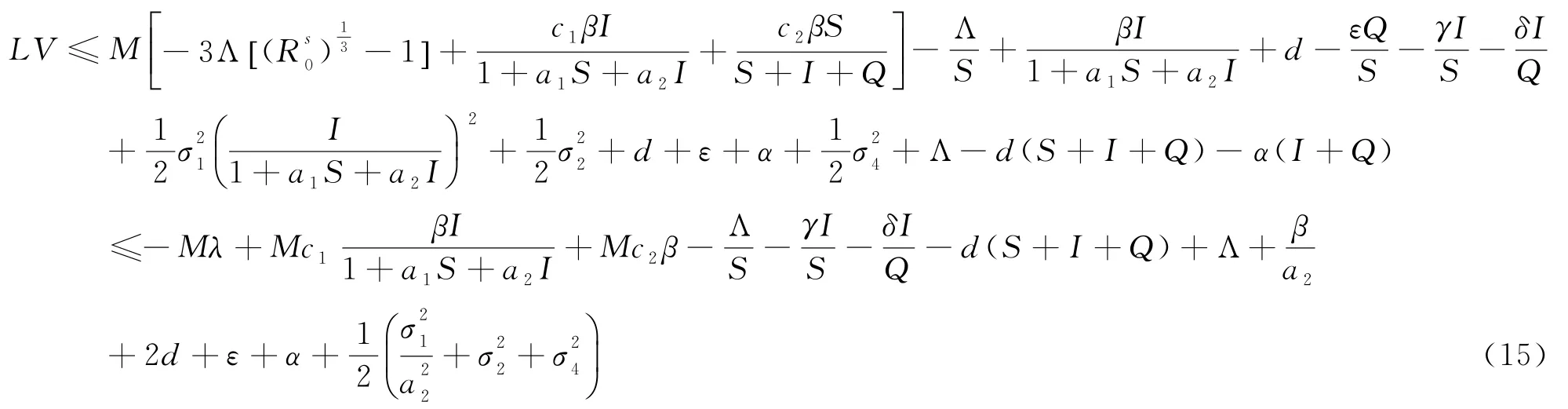
接下來考慮下面4種情況.

情況1：如果(S，I，Q)∈D1，有

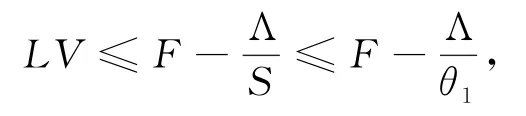
綜合(9)可得

情況2：如果(S，I，Q)∈D2，有

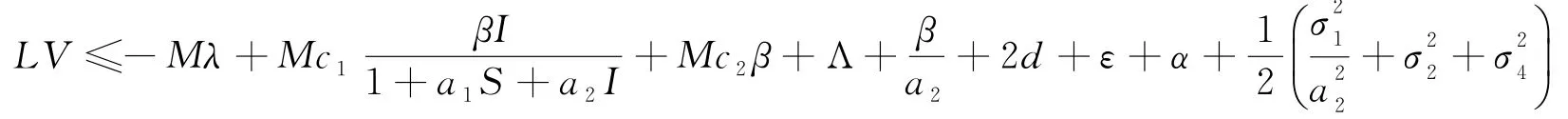
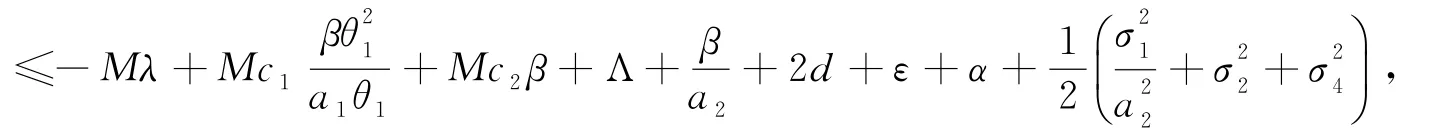
因此

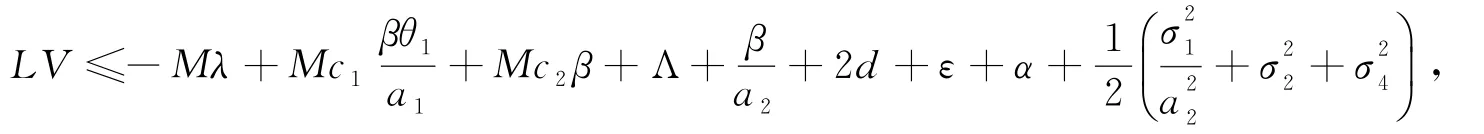
情況3：如果(S，I，Q)∈D3，有

情況4：如果(S，I，Q)∈D4，有

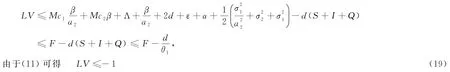
結合(16)(17)(18)(19)可知，系統(2)存在遍歷性平穩分布，即疾病持久.

3 疾病的消亡

流行病爆發時，不只需要研究疾病的持久性，更重要的是討論疾病在什么條件下消亡，本節主要討論系統(2)的消亡.

定理3如果對于任意給定的初值是系統(2)的解，若

證明：應用It?公式可得

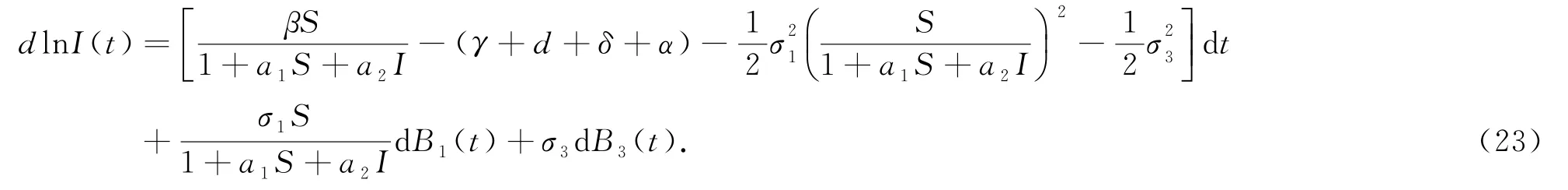
對(23)式從0到t積分得

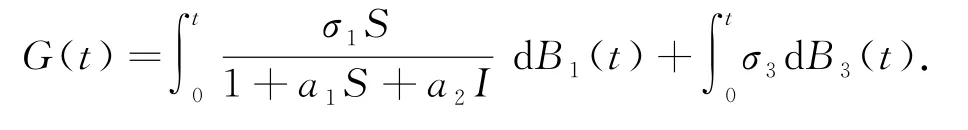
考慮在條件(21)下，

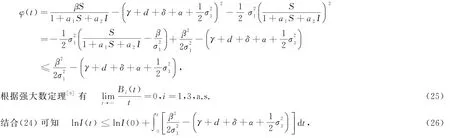
對(26)式兩邊同除以t并令t→∞，又由(25)有

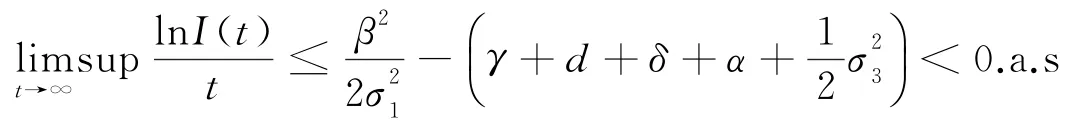
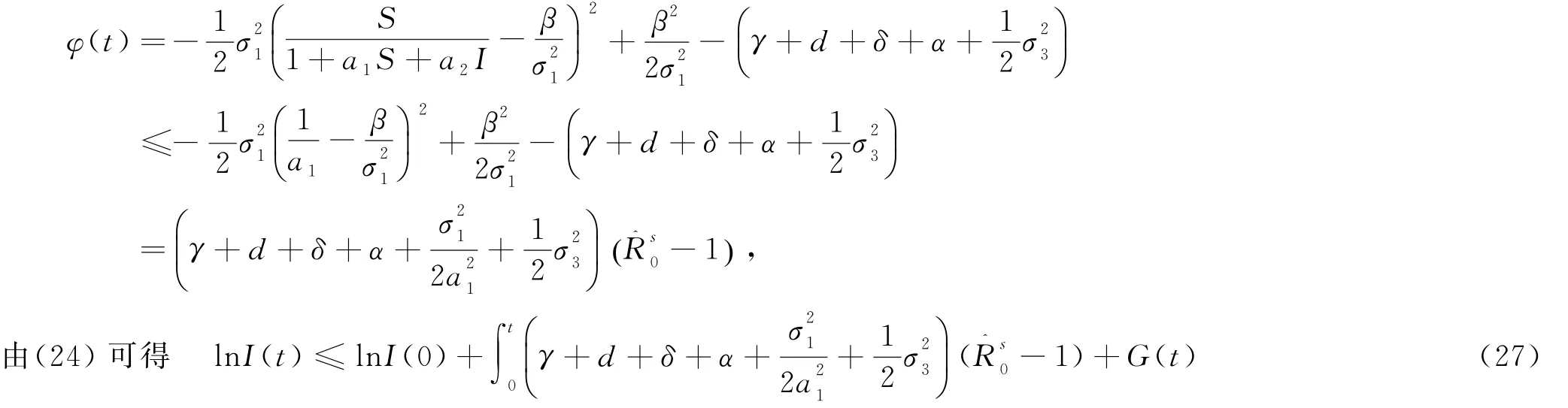
對(27)式兩邊同時取極限并除以t，由(22)(25)，則

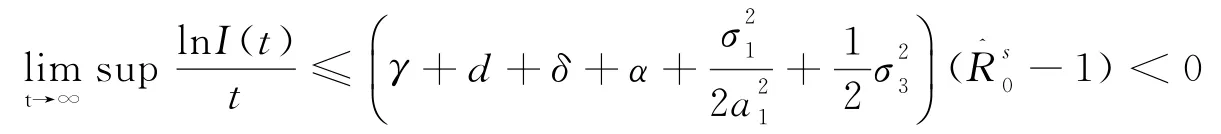
4 數值模擬與結論

利用Euler Maruyama(EM)方法[10]和Matlab軟件數值模擬在不同白噪聲下疾病遍歷平穩分布和消亡問題，首先給出系統(2)的離散化形式：

其中ζk(k=1，2，3，…)是服從N(0，1)分布的高斯隨機變量.

考慮疾病的遍歷平穩分布，參數取值如下：Λ=1，d=0.2，β=0.66，a1=1，a2=1，σ1=0.01，σ2=0.002，σ3=0.2，σ4=0.3，δ=0.1，α=0.01，γ=0.1，ε=0.004，

由圖1可知疾病持久，驗證了定理2.

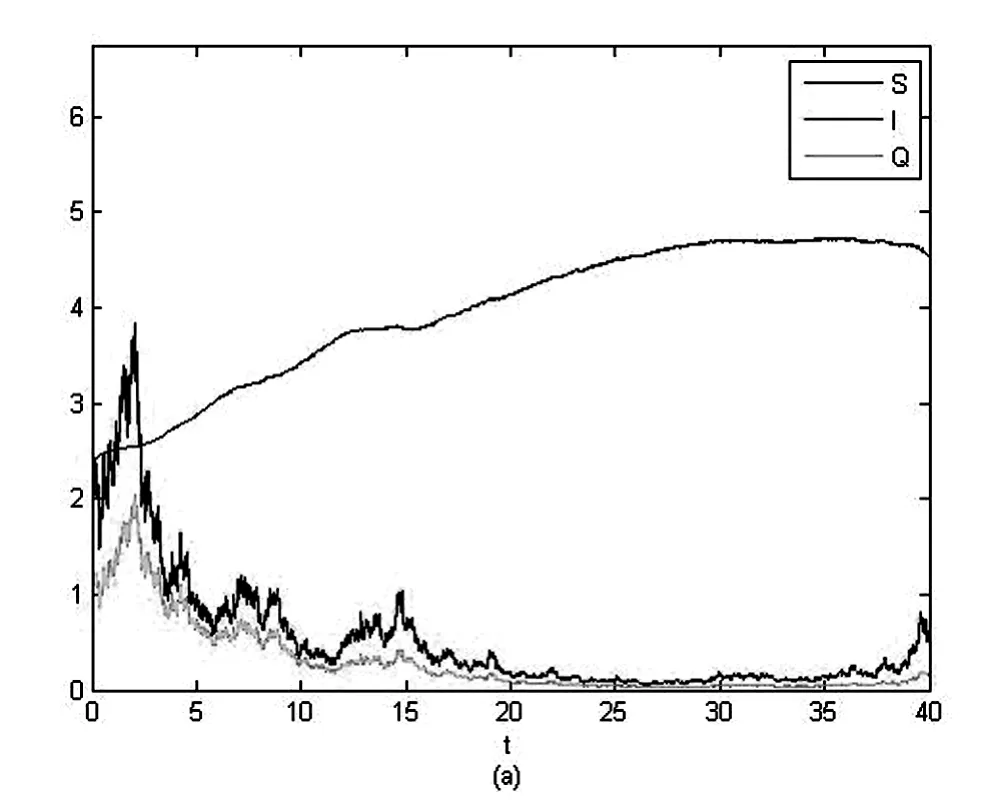
圖1 系統(2)在初值為(2.4，2.4，1.2)時S(t)，I(t)，Q(t)的軌跡圖Fig.1 The path of S(t)，I(t)，Q(t)for system(2)with initial values

考慮疾病的消亡情況，取參數如下：Λ=0.1，d=0.15，β=0.15，a1=1，a2=2，δ=0.004，α=0.25，γ=0.1，ε=0.004，σ2=0.002，σ3=0.2，σ4=0.3.

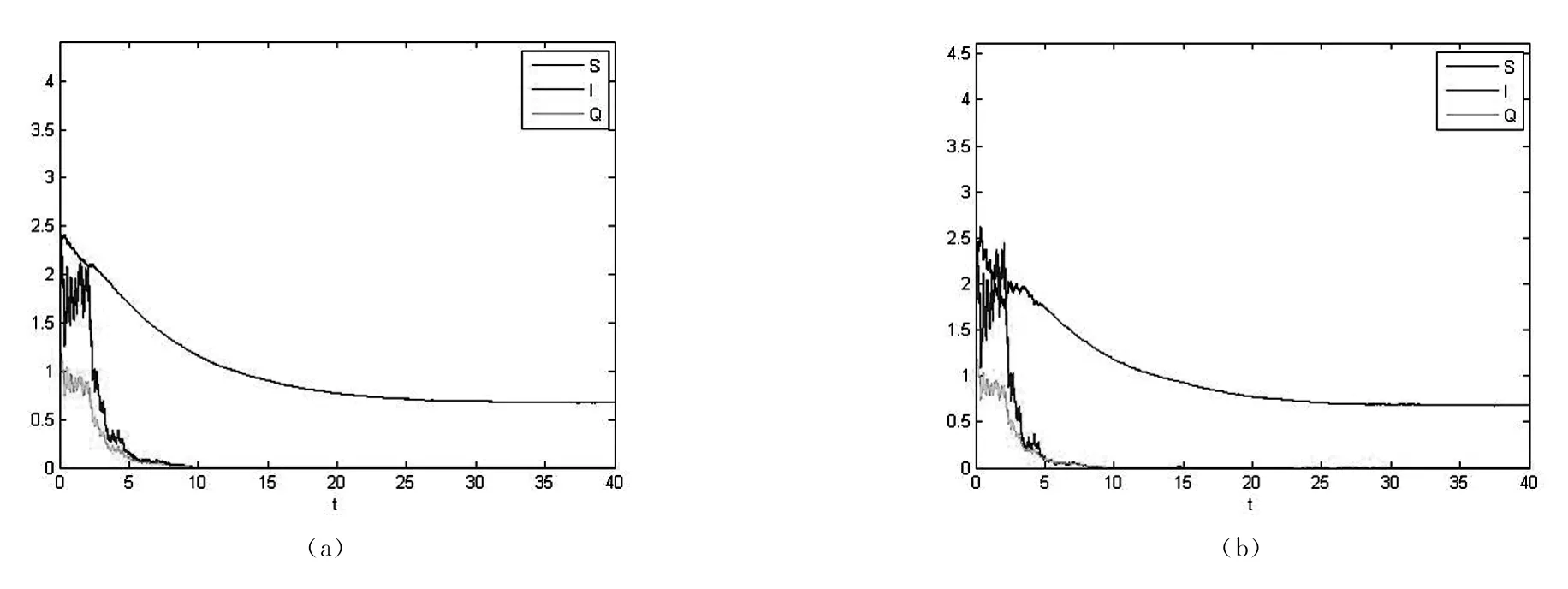
圖2 系統(2)在初值為(2.4，2.4，1.2)和σ1 分別為0.1(a)，0.45(b)時S(t)，I(t)，Q(t)的軌跡圖Fig.2 The path of S(t)，I(t)，Q(t)for system(2)with initial values with(2.4，2.4，1.2)

本文主要討論了Beddington-De Angelis發生率的SIQS傳染病模型的動力學行為，證明了隨機系統(2)存在唯一的全局解，得到了基本再生數在一定條件下可控制疾病遍歷性平穩分布和消亡，并且發現大的隨機白噪聲會抑制疾病的爆發，這在生物學意義上為我們提供了控制疾病的有效方法.