一種變結構電動汽車電子差速控制方法研究*

劉 恒宋偉奇韋彬貴

(1.柳州職業技術學院，廣西 柳州545006;2.柳州城市職業學院，廣西 柳州545036)

隨著人們對環境改善的需求增加，近年來，電動汽車市場逐漸走俏，受到消費者的普遍歡迎.由于電動汽車采用電機替代傳統的變速器、減速器等機械設備，不僅提高了傳統效率，而且降低了環境污染.[1]由于電動汽車是通過電機對車輪的單獨控制，其動力學特性獨特，為了保證行駛的穩定性，需要精確的內外輪差速控制策略.[2]因此，電動汽車的電子差速控制技術成為該領域的熱點研究內容.[3-5]

電子差速的基本原理是利用經典的控制方法對電動汽車驅動輪的精確控制，從而滿足汽車運行的穩定性需求，提升車輛運行的穩定性和舒適性.[6]近十年來，國內外研究人員對電子差速的控制方法進行了深入的研究.例如，文獻[7]基于傳統的PID控制器，構建了四輪的差速約束方程，并實現了電子差速的精確控制，但是該控制方法要求時速低于10 km/h，且輪滑率小于預先設定的閾值;文獻[8]將轉速作為優化目標，采用門限閾值的方法對行駛車輛的滑移率和轉向角進行控制，但是控制范圍需要在設定的閾值范圍內;文獻[9]針對前輪驅動情況的差速系統展開研究，采用流量控制法實現了汽車轉矩的自適應直接控制，并構建了用于實驗驗證的半實物平臺.

縱觀國內外研究現狀，目前，電子差速控制主要集中在驅動輪的轉速控制、滑移率的求解和轉矩的解析表示三個方面，忽略了車輛整體狀態的穩定性.因此，本文立足車輛穩態需求，針對車輛在快速轉彎情況下的差速控制問題展開研究，在建立整車仿真模型的基礎上，提出了基于橫擺參量的滑模變結構控制方法.最后，基于構建的整車系統模型進行了詳細的仿真分析，證明本文方法具有較優秀的控制性能.

1 模塊化建模原理

1.1 輪轂電機模型

輪轂驅動電機模型是整車仿真的重要模塊，模擬當前研究中通用的系統模型，采用永磁無刷直流電機構建驅動電機模型.假設輸入電壓為三相a、b、c，在a、b導通c斷開的情況下，滿足

可以將輪轂模型的平衡電壓方程表示為

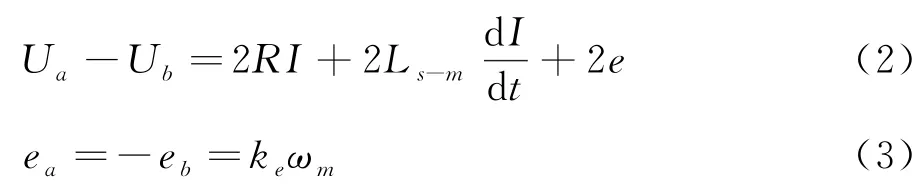
電磁轉矩為

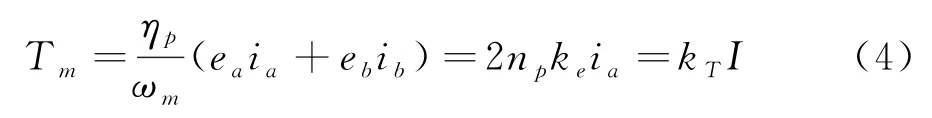
輪轂電機的動力學模型為

其中，U a、U b、U c為系統模型輸入的三相電壓值，e a、e b、e c為反電動勢值，其系數為k e，i a、i b、i c為三相定子電流值，R為各相等值的電阻，各相繞組的自感與互感之差為L s-m，ωm、n p和k T分別表示電機的轉速、極對數和轉矩系數，J m為轉動慣量，T L表示電機的負載轉矩.

假設U=U a-U b，根據式(2)-(5)可以將轉動電機的狀態空間模型表示為

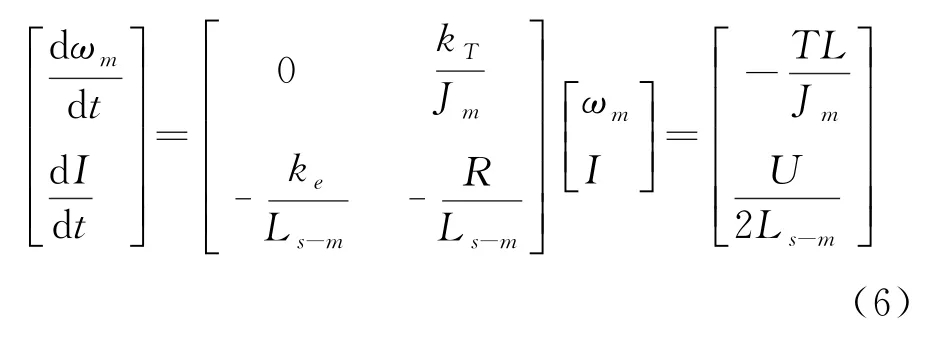
1.2 駕駛員運動模型

為構建整車仿真系統，構建駕駛員運動仿真模塊是十分必要的，參考文獻[10]的研究，構建如圖1所示的運動系統模型.其系統的輸入兩為目標車速和實際車速的差值，輸出參量為驅動輪轂的控制參量.為便于系統的穩定，在模型中引入了約束條件.

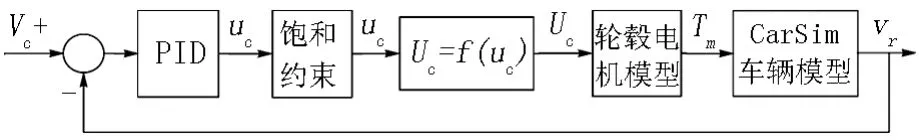
圖1 駕駛員運動模型Fig.1 Driver Motion Model

2 提出的滑模變結構控制方法原理

2.1 車輛穩態橫擺角速度參量

為便于推導橫擺控制參量，采用如式(7)描述的線性而自由度模型

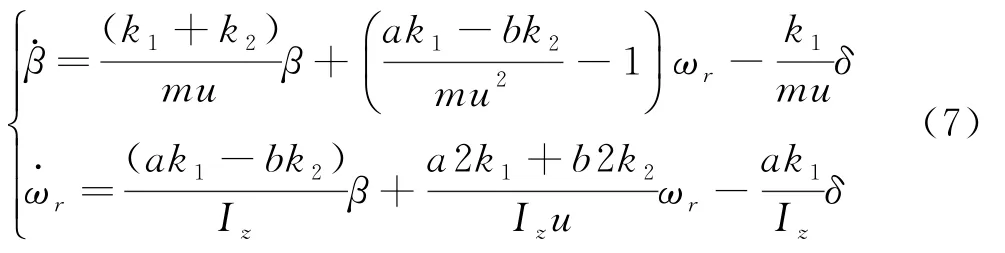
則橫擺角速度參量對驅動輪轉角輸入的響應為

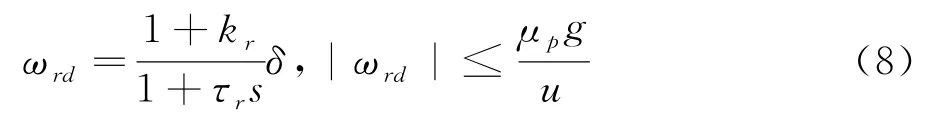
為了計算測量穩態參量，要求在穩態區域內，車輛側向加速度滿足a y＜μp g，進而可以將車輛穩態情況下的速度增益可以計算為

其中，K為穩定因子，式(7)～(9)中各參量的具體含義見表1.

表1 參量說明Tab.1 Description of parameters

2.2 電子差速的變結構控制設計

滑模變結構控制屬于非線性控制問題，由于控制參量不是連續變化，可以對連續變化的非線性系統狀態進行有節奏的優化和調整，進行保證目標軌跡控制在閾值范圍內.同時，由于滑模變結構的狀態參量與初始狀態及外界擾動無關，因此具有非常高的穩定性.為便于分析變結構特性，可以將(7)式改寫為

其中

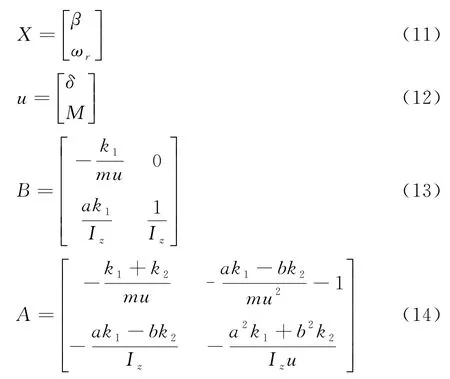
一旦汽車進入滑動轉臺，其控制力矩可以計算為

計算誤差

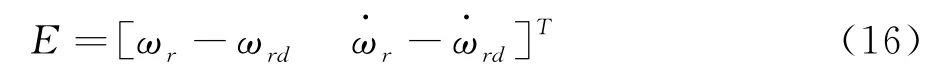
變化函數

變化函數的系數矩陣C=[c1]，為保證系統快速進入滑模狀態，可以采用指數趨近的方式對軌跡進行限制，即

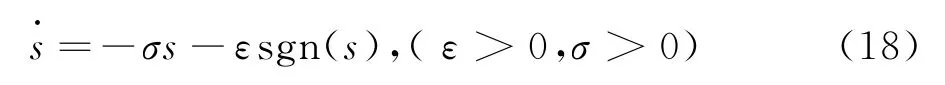
式中，ε為系統臨近s=0時候的速度，σ為趨近速度的變化范圍參量，為了防止切換過程中產生較大的抖動，采用傳統的飽和函數sat替代目前研究中常用的切換函數sgn，進而可以將本文提出的滑模控制反饋參量表示為

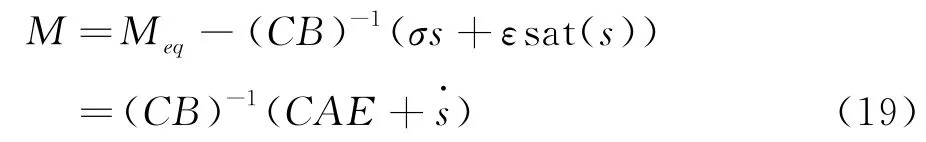
其中

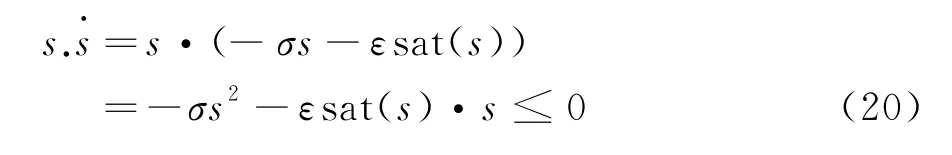
3 計算機仿真分析

3.1 仿真模型說明

為驗證本文方法正確性和優越性，建立了如圖2所示的整車仿真模型，仿真中具體參量的設置如表2所示.

3.2 仿真分析

針對構建的模型系統分析了車速60 km/h情況下的參量輸入及變化控制情況，主要針對理想情況，不引入差速控制和本文方法控制的結果進行了對比.如圖3、圖4和圖5所示.其中，圖3為車輛行駛的仿真軌跡，主要是模擬在快速行駛狀態下轉彎情況的穩定性和差速的控制精度.從圖3中曲線可以明顯看出，在不引入電子差速控制情況下，其轉彎半徑要明顯大于引入差速控制情況下的轉彎半徑，因此，引入本文差速控制方法以后，轉彎性能得到了較大的改善和提升.其主要原因是，是因為引入差速控制以后，在轉彎的情況下驅動力矩不再是平等分配，而是根據實際的附著要求自適應的調整.圖4為驅動力矩的示意圖曲線，從圖4中可以看出，在左轉的情況下，右側(外側)輪轂的轉動力矩要明顯大于左側(內側)的轉動力矩，此時，測量的控制系統引入了橫擺參量的控制，保持車輛的穩定性能.圖5為橫擺角速度的變化曲線，從圖5中可以看出，橫擺角速度的很好地擬合了理想狀態，從整個曲線中可以明顯看出本文方法的優點，不僅是相應的速度上，還是最后穩定的橫擺參量值方面都維持在了最優的狀態.當然，從圖5中曲線也可以看出，穩定狀態之前有一定的振蕩和偏差，這主要是由于觀測器本身的噪聲引起，在后續的工程應用中可以通過增加濾波器的方式對穩態失調進行校正.

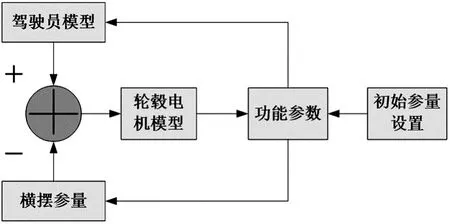
圖2 仿真原理框圖Fig.2 Simulating schematic block diagram

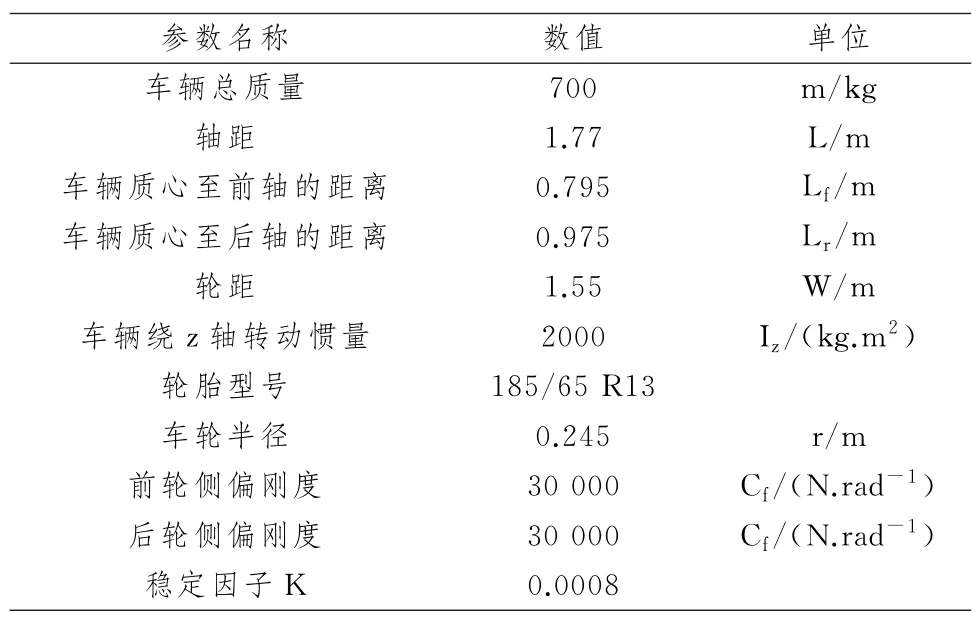
表2 仿真參數設置Tab.2 Settings of simulation parameters

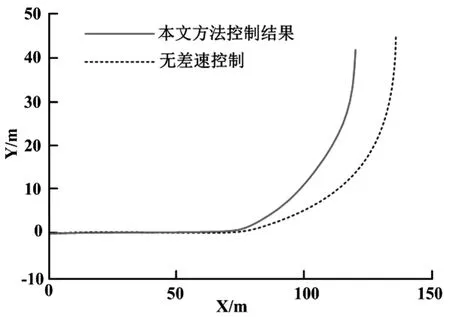
圖3 仿真軌跡Fig.3 Simulation trajectory

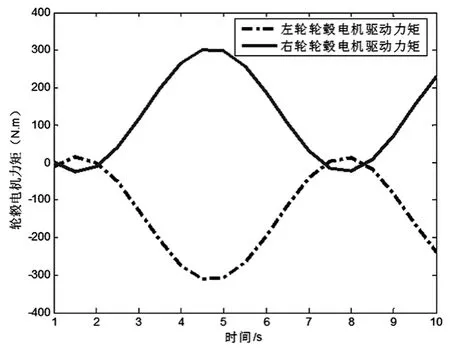
圖4 驅動力矩曲線Fig.4 Driving Torque Curve

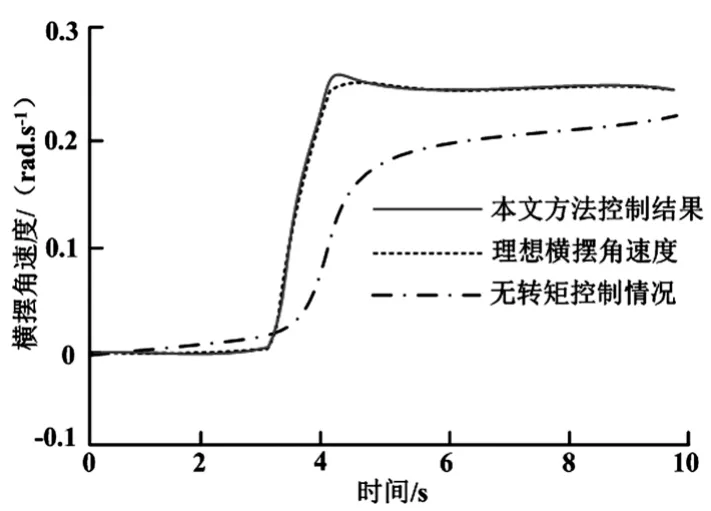
圖5 橫擺角速度變化曲線Fig.5 Yaw Angular Velocity Change Curve

4 結語

電動汽車已經成為當前綠色出行的首選代步工具，但是如何改善其運行的舒適性一直是業界研究的熱點.本文主要基于轉向情況下的車輛穩定性能需求，提出了一種模塊化設計的變結構電子差速控制方法.構建了相應的輪轂電機模型和駕駛員運動模型，并分析了電子差速控制的參量方程，搭建了整車仿真系統.結果顯示了本文方法在差速穩定控制方面的優勢，保證了轉彎狀態的效果和穩定性.但是，也顯示了該方法在狀態變換時刻的穩態振蕩問題，這一點需要在后續的研究中加以改善和研究.