基于極限學習機的電力短期負荷預測
文/汪威為 陳超洋 陳祖國 盧明
1 引言
負荷預測是電力系統經濟調度中的一項重要內容,是能量管理系統(EMS)的一個重要模塊。電力系統短期負荷預測是目前電網調度、制定發電計劃及電廠報價的主要依據,對電力系統的運行、控制等有著重要的影響。準確的負荷預測對保持電網的安全穩定運行、降低發電成本、提高電力系統的經濟效益和社會效益至關重要。本文針對電力系統短期負荷預測問題,通過結合極限學習機和粒子群算法,設計了一種簡單、高效的新型短期負荷預測算法。
2 PSO-ELM介紹及設計
2.1 極限學習機簡介及設計
極限學習機(ELM)是由Huang.G.B等提出的,具有收斂速度快、泛化能力強等優點,在高度非線性建模中得到了廣泛的應用。ELM是一種新型的快速學習算法,對于單隱含層神經網絡,ELM可以隨機初始化輸入權值和偏置并得到相應的輸出權值。對于一個單隱層神經網絡,假設有N個任意的樣本(xj,tj),其中:

對于一個有L個隱層節點的單隱層神經網絡可以表示為:

為輸入權重,βi為輸出權重,bi是第i個隱層單元的偏置。(xj,tj)表示訓練樣本。極限學習機能無限逼近學習樣本,即神經網絡學習的目標是使得輸出的誤差最小,可以表示為:
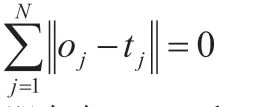
即存在W,β和b使得:
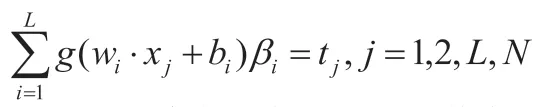
可以用矩陣表示為:Hβ=T。其中,H是隱層節點的輸出,β為輸出權重,T為期望輸出。
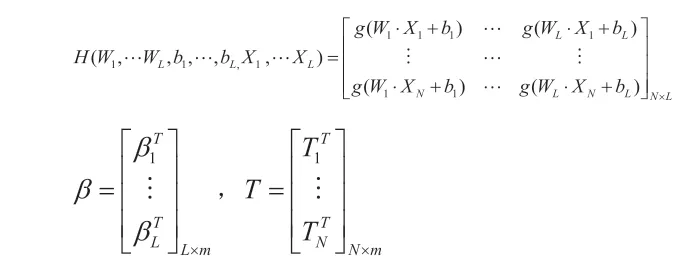
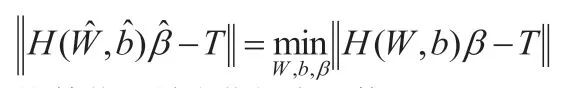
這等價于最小化損失函數:
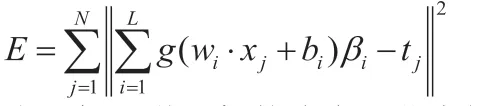
由于極限學習機的隱含層節點輸入權值和閾值為隨機取值,為了克服取值隨機性帶來的誤差,提高模型的泛化能力,利用改進的粒子群算法(PSO)對隱含層節點輸入權值和閾值進行全局尋優。
2.2 粒子群算法優化極限學習機介紹及設計
粒子群算法近年來受到了極大的關注和研究,并取得了豐碩的成果。不同于以往的研究,本文基于粒子群算法對極限學習機參數進行優化,結合兩者優點,并設計相應的優化算法,具體如下。
極限學習機的隱含層節點輸入權值和閾值為隨機取值,隨機取值可能使部分輸入值為0或近似為0,從而使部分隱含層節點失效,因此需使用參數設定其范圍,同時為了保證粒子的活性和跳出局部最優,對粒子群算法進行改進。首先確定粒子群算法參數,包括種群大小、最大迭代次數、學習因子等;其次確定適應度函數,一般取訓練樣本與模型擬合值的均方差為適應度函數;初始化種群,種群中的每一個粒子代表一個解,每個粒子包含輸入權值矩陣和閾值向量信息;然后更新種群,根據改進后的粒子群算法對粒子位置和速度進行更新,若粒子處于停滯狀態,則對粒子位置和速度進行初始化;然后再更新粒子歷史最優值和全局最優值;最后滿足迭代結束條件時停止迭代,輸出預測結果。模型總步驟如下:

表1:試驗模型預測誤差對比
Step1: 初始化。初始化粒子群參數,設定極限學習機學習參數。
Step2: 計算。根據粒子信息值,以及樣本數據進行計算,經極限學習機得預測值。依據得到的預測值,計算出適應度值,同時記憶群體和個體各自所適應的最佳位置和。
Step3: 算法優化。將 Step2 中得到的適應度值與全局最優解比較,更新適應度函數及其對應的權值和閾值。
Step4: 迭代更新。將粒子群算法優化的參數返回給極限學習機。
Step5: 判斷。判斷終止條件是否滿足,若滿足則直接終止循環,否則返回 Step2。
3 實例驗證
3.1 優化前后的ELM模型的比較
選用2003年3月1日至2003年9月25日,共5000組數據進行測試。PSO-ELM算法參數,最大迭代次數為250,種群大小為120,輸入層節點數為2,隱含層節點數為5,輸出層節點數為1,權值范圍為0.3~0.9,慣性因子、學習因子分別為2.8和1.3。算法獨立運行250次后的結果如圖1所示。
通過圖1及表1試驗模型預測誤差對比,可知PSO-ELM優化模型測試樣本的仿真誤差為:43933.2795,ELM模型測試樣本的仿真誤差為:128327.3217;PSO-ELM優化模型的決定系數R2為0.8125,ELM模型的決定系數R2為0.27455 PSO-ELM優化模型的預測效果要明顯優于ELM原始模型的預測效果。
將極限學習機用戶電力負荷預測中,為客服極限學習機因隱含層輸入權值與閾值隨機取值帶來的誤差,利用改進的粒子群算法對其進行最優尋值。最后的實例結果表明,PSOELM模型與算法不僅可行、有效,而且具有較強的學習能力。在驗證優化后的預測模型性能后,進一步將其與常用的BP神經網絡性能做分析比較。
3.2 與BP神經網絡模型的比較
Bp程序設計如下:
圖1:PSO-ELM模型誤差曲線
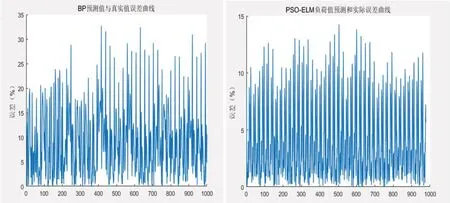
圖2:誤差比較
本例數據是每小時一組數據,將每天24小時所測數據看做整體進行數據的輸入,由于輸入包括時間、負荷以及溫度三個變量,所以輸入層節點數為:24*3=72個。想要的輸出是下一天的電力負荷,,所以輸出層節點數是1個,隱藏層設計為二層,第一層3個節點,第二層4個節點.其余參數設計如下:最大訓練次數為100,訓練精度要求為0.0005。與BP神經網絡的預測效果比較圖如圖2所示。
圖2為預測值與真實值的誤差曲線曲,可以體現真實值與預測值之間的誤差情況,通過對比可以看出,PSO-ELM預測值的誤差要明顯低于BP神經網絡所預測的值,且PSOELM預測值誤差的波動范圍較小,進一步驗證了PSO-ELM模型對電力負荷的預測性能。

