基于遺傳算法的永磁同步電機自抗擾控制

2019-06-11 08:50:08

浙江工業大學學報 2019年4期

(浙江工業大學機械工程學院，浙江杭州 310014)

永磁同步電機(Permanent magnet synchronous-motor, PMSM)具有結構簡單、工作效率高等特點，在工業、交通、軍事和航空等重要領域得到廣泛應用[1]。但永磁同步電機存在強耦合、參數易變和非線性等特點[2]，要考慮參數及負載變化對控制性能的影響。目前常用的控制策略如PID控制[3]，它是以系統的偏差進行控制，控制簡單，易于實現，但是PID是采用線性方法，對于非線性系統來說，在抗擾動方面難以實現高精度的控制[4-5]。

電機運行過程中的負載、參數變化等因素[6]限制了經典PID控制方法的應用范圍。如果是固定擾動，可以通過前饋環節對擾動進行補償，但在實際應用中，擾動往往是變化的，不可測量的，對系統造成不可估計的影響，所以要對系統內外擾動進行觀測，以便系統根據得到的數據及時作出調整。自抗擾控制(ADRC)不依賴于被控對象準確的數學模型[7-9]，系統內部及外部擾動由觀測器觀測出來并加以補償，所以對系統參數變化和外部擾動不敏感；同時，ADRC控制器還設置了跟蹤微分器和非線性狀態誤差反饋控制[10-14]，實現無超調快速跟蹤。筆者在矢量控制與PID控制[9]的基礎上采用ADRC技術對永磁同步電機進行控制。該系統可實現位置、速度和擾動的觀測，用ADRC控制器代替矢量控制中的位置和速度控制器，電流環采用PI控制器。

1 問題描述

PMSM在兩相同步旋轉d—q坐標系下，采用id=0矢量控制策略[10-14]，電機運動方程為

(1)

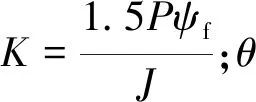
ADRC的二階控制對象為

(2)

式中：u為系統控制量；b為u的系數；f(x)為系統總擾動。

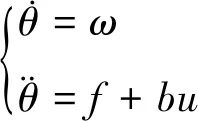
(3)

將PMSM數學模型轉化為

(4)

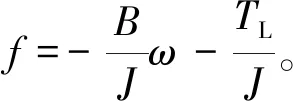
2 PMSM的ADRC位置控制器設計

ADRC由3 部分組成：安排過渡過程、擴張狀態觀測器和非線性組合[7]，結構框圖如圖1所示。

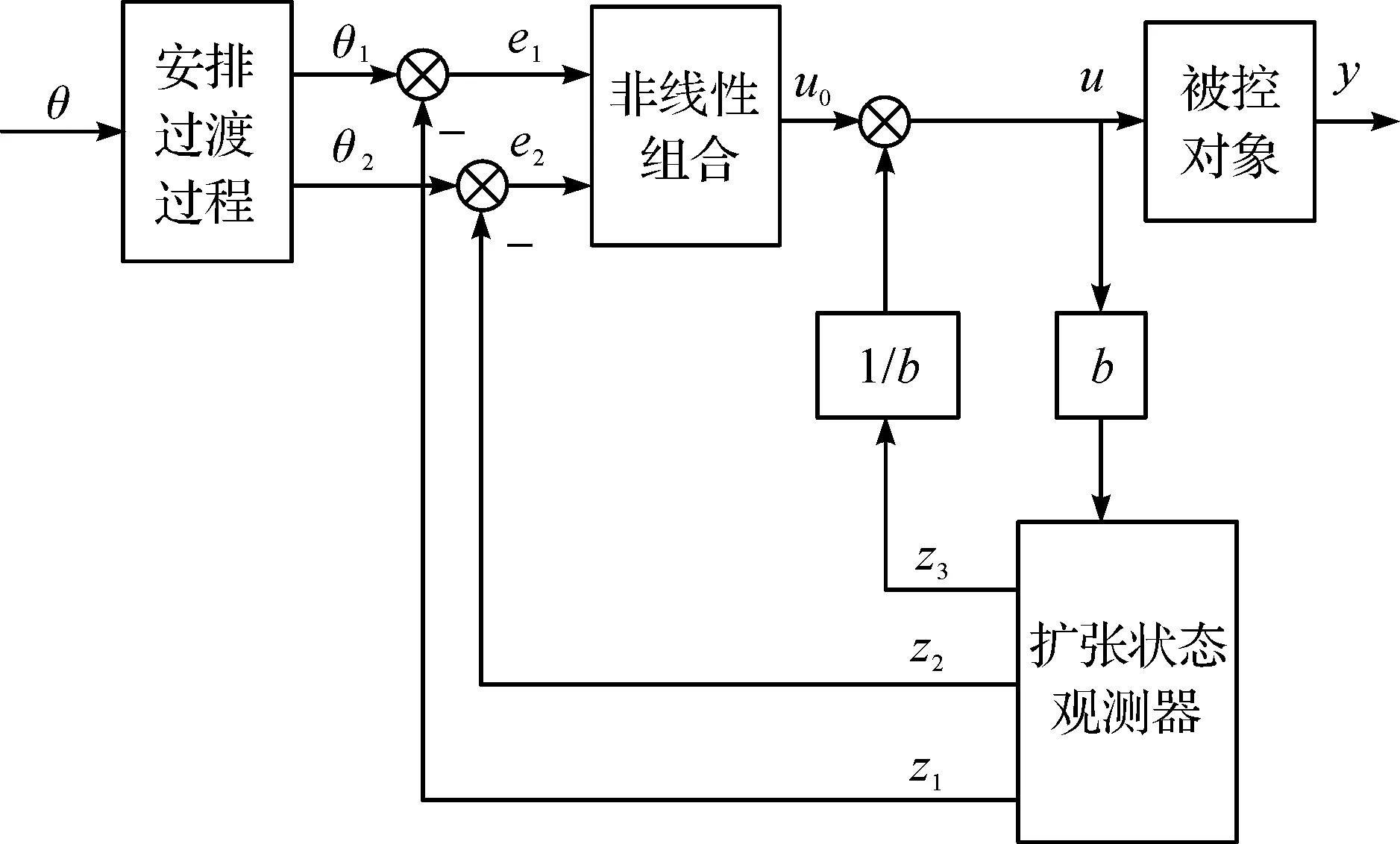
圖1 二階自抗擾控制器結構框圖Fig.1 Structure block diagram of two order auto disturbance rejection controller

在對系統狀態進行觀測之前，需要設計一個微分器來實現過渡，使系統可以無超調跟蹤，微分器采取近似微分的方法來實現。

跟蹤微分器(TD)形式為

(5)

式中：h為采樣周期；e0為位置跟蹤誤差；r為可調系數，r越大上升越快。fst函數為

(6)

其中

(7)

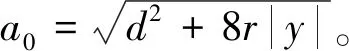
擴張狀態觀測器(ESO)[6]是整個自抗擾控制系統的關鍵部分，它能觀測系統狀態和擾動，實時反饋給系統進行補償，其表達式為

(8)

其中

式中：z1，z2，z3分別為位置θ，速度ω還有總擾動f的估計值。

補償后系統控制量為

(9)

為了克服系統擾動，提高系統魯棒性，自抗擾控制器的非線性組合采用基于模型的PI魯棒控制[15]。

由前面所述，永磁同步電機伺服系統描述為

(10)

位置跟蹤誤差為e1=θ-z1，速度跟蹤誤差為e2=ω-z2，定義誤差函數為e=e2+5e1，定義x=e+z2，則有

(11)

控制率設計為

(12)

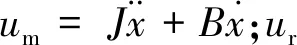
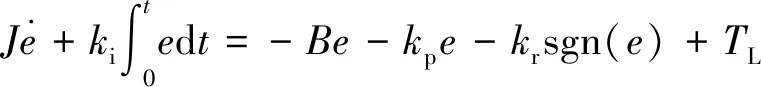
(13)

其中

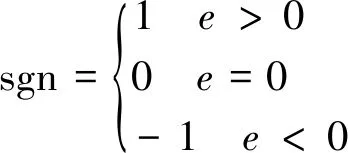
下面進行穩定性分析，取Lyapunov函數為

(14)

對V進行求導，并將式(13)代入，可得

(15)

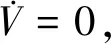
基于矢量控制[8]的PMSM自抗擾位置控制器系統框圖如圖2所示。

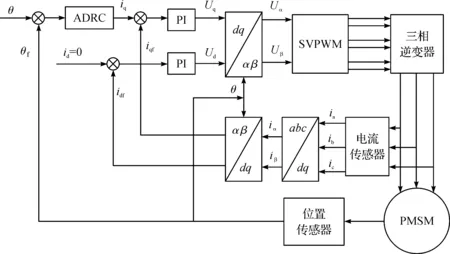
圖2 ADRC位置控制器系統框圖Fig.2 Block diagram of ADRC position controller system

3 基于遺傳算法的ADRC參數優化

上述ADRC控制器待優化的參數有ESO的β1，β2，β3，考慮系統整體穩定性的要求，觀測器的觀測值應該盡可能接近系統的實際狀態，所以，遺傳算法的目的是使觀測的位置和總體擾動誤差盡可能低。將遺傳算法適應度函數選擇為位置誤差及總和擾動誤差的平方根值，設計適應度函數為

(16)

式中：N為種群個體數，這里N=50；w1，w2為權重，w1=0.7，w2=0.3。

1) 參數編碼：將待優化的參數β1，β2，β3作為個體的3 個基因進行編碼[16]。隨機產生個體數為50的初始種群Ai(i=1，2，…，50)，初始種群是參數假設解的集合，最優參數從這些初始種群出發，經過一系列遺傳算法優化求出。種群的搜索范圍為β1∈[0,200]，β2∈[0,800]，β3∈[0,1 800]。

2) 選擇：選擇的目的是將有用的遺傳信息保留下來，提高收斂速度。個體選擇采用最佳保留選擇，即將輪盤賭方法選擇的當前群體中使適應度函數小的群體[17]，遺傳到下一代群體中。

3) 交叉和變異：交叉即按照概率Pc選擇2 個基因進行同位置的染色體互換；變異即按照概率pm對基因某些位進行取反[18-19]，即0變1，1變0。交叉概率Pc和變異概率Pm的選擇按照自適應調整的方法進行，這樣可以避免固定的交叉變異概率值對環境的不適應，2 個值分別進行適應度調節，即

(17)

(18)

式中：fmax為適應度最大值；favg為每代適應度均值；f為兩個交叉個體中適應度最大值；f*為變異個體的適應度值。

4) 全局最優收斂：當遺傳代數達到設定值或者適應度值不再劇烈變化時，則算法結束，全局收斂，否則返回2)循環執行。最終得到優化后的參數值為β1=103.95，β2=398.57，β3=1 132.26。

遺傳算法流程圖及優化框圖分別如圖3，4所示。

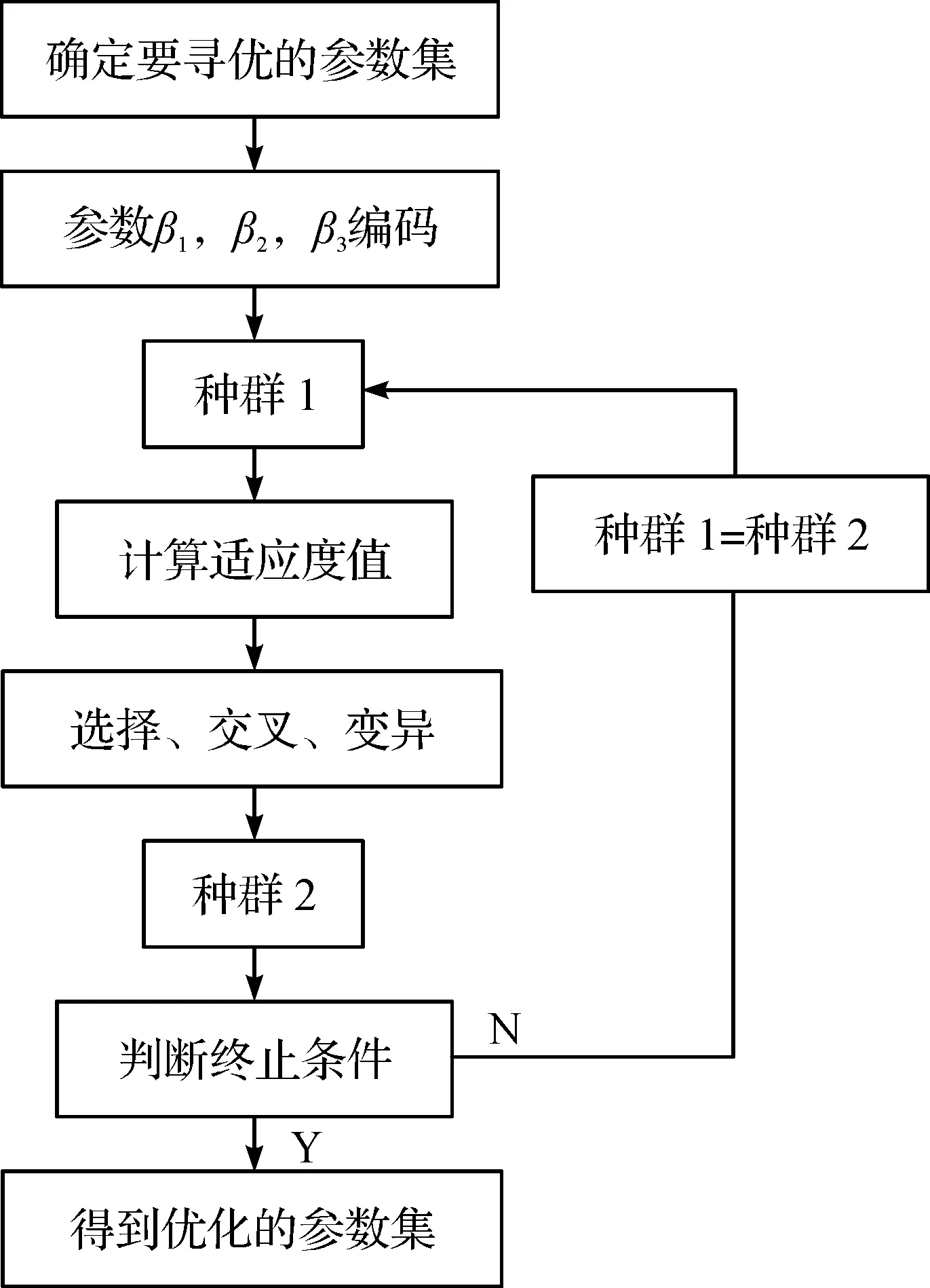
圖3 遺傳算法流程圖Fig.3 Flowchart of genetic algorithm

圖4 遺傳算法優化ADRC參數框圖Fig.4 Block diagram of optimizing parameter of ADRC by genetic algorithm

4 仿真及實驗分析

永磁同步電機的負載和參數隨環境不同而改變，因此仿真中要研究加負載和參數變化時系統的定位精度。在Matlab/Simulink中搭建仿真模型，采用位置環自抗擾控制器，仿真步長h=0.001 s。仿真中所用的PMSM參數如表1所示。

表1 電機參數表Table 1 Motor parameter

ADRC的部分參數采用遺傳算法進行優化，為了驗證優化后控制器的性能，仿真中其他條件相同，給定位置為5 °，10 °時，比較遺傳算法優化后的ADRC控制器與經驗整定參數的ADRC控制器的控制性能。對比圖如圖5所示。

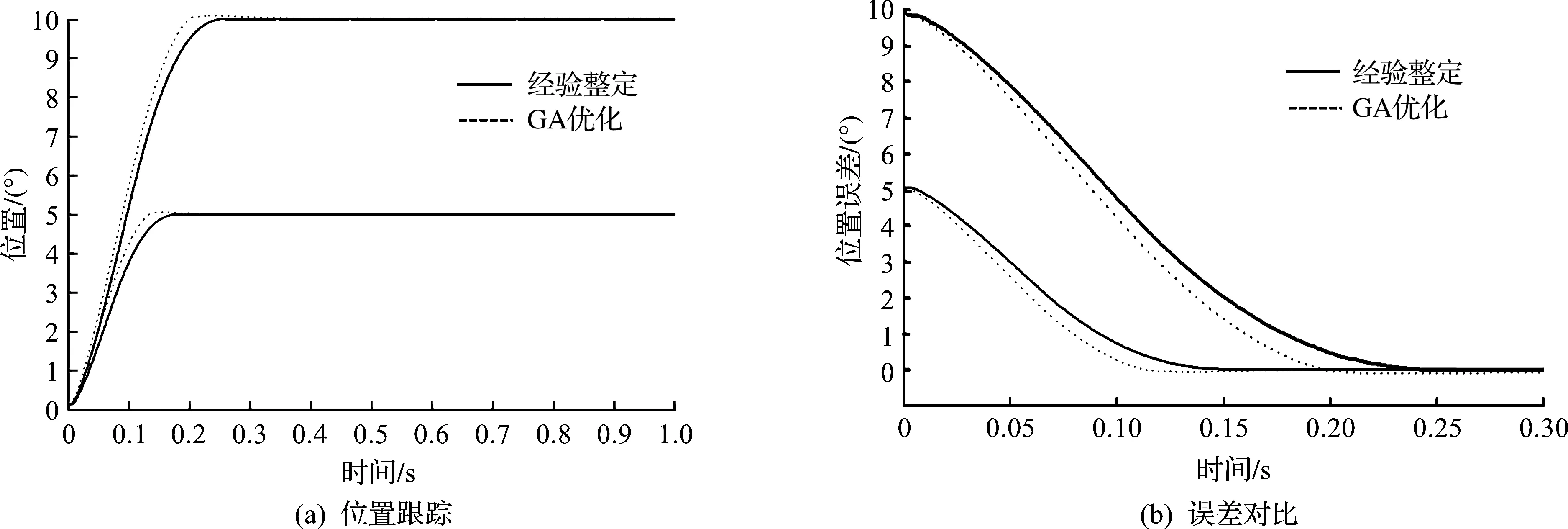
圖5 GA優化前后系統位置跟蹤Fig.5 System location tracking before and after GA optimization

由圖5可得：經過遺傳算法優化后的系統跟蹤速度明顯高于未優化的系統，跟蹤誤差低于后者，位置為10°，5°時調節時間比經驗整定參數的系統分別快0.04，0.03 s。下述關于ADRC位置控制器系統仿真均是優化后ADRC位置控制器。

系統參數轉動慣量的變化可能會對控制穩定性造成影響，為了驗證ADRC控制系統在參數變化環境下的跟蹤精度，給定信號相同時，比較轉動慣量為J，2J時系統的位置跟蹤情況，如圖6所示。

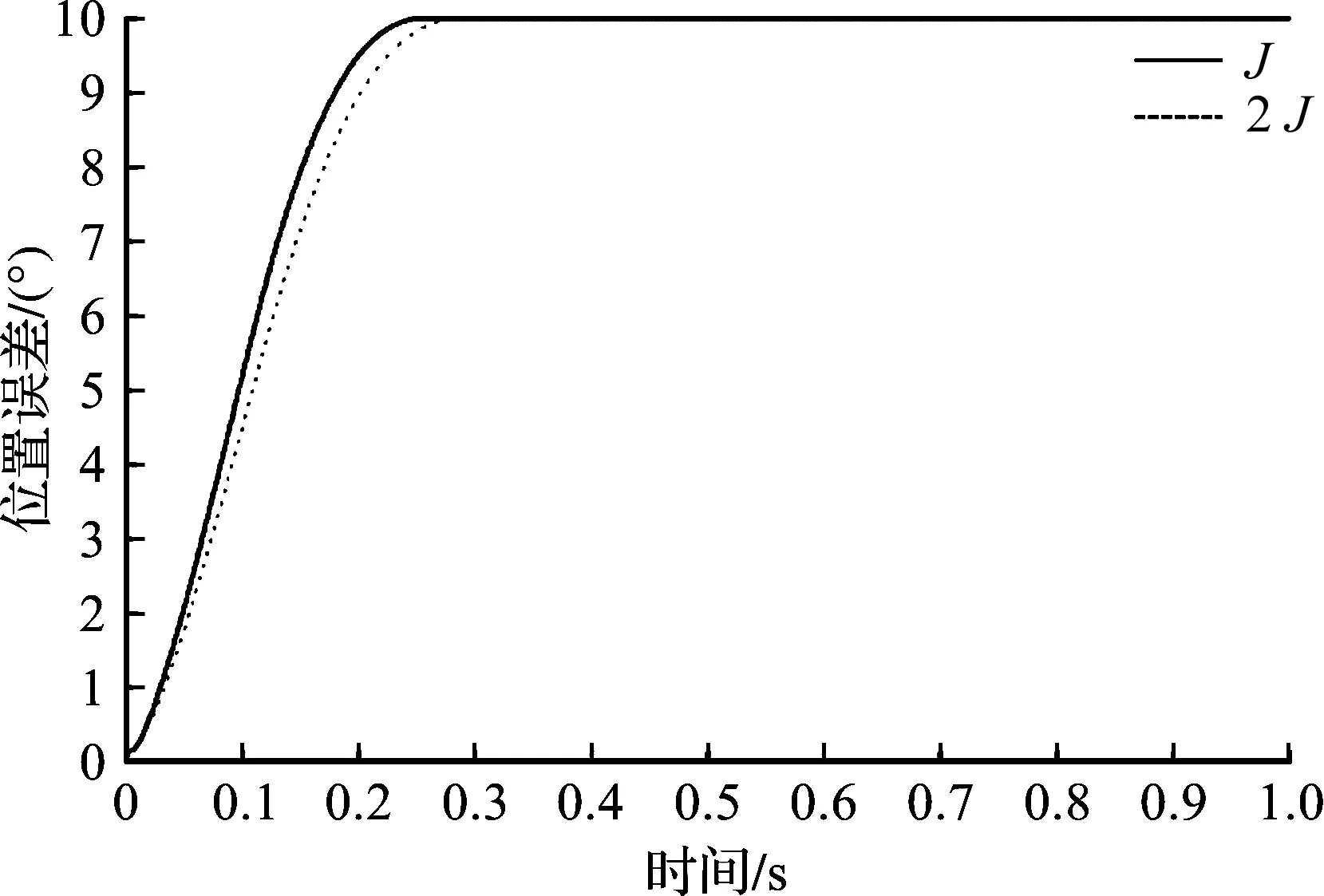
圖6 轉動慣量分別為J和2J系統位置跟蹤Fig.6 Position tracking when the moment of inertia are J and 2J

從圖6可得：當系統參數轉動慣量變為2J時，調節時間僅下降0.014 s，系統的位置跟蹤依然快速穩定，說明系統慣量變化不影響該控制器的性能。

為了驗證優化后的ADRC系統在加載后的抗干擾性，其他條件完全相同的情況下，仿真對比了階躍信號下PID和ADRC控制器在t=0.3 s加載0.2 N·m，t=0.5 s卸載，結果如圖7所示。

圖7 PID與ADRC控制系統抗干擾性能對比Fig.7 Comparison of anti-jamming performance between PID and ADRC

由圖7可得：PID控制與ADRC控制相比，到達穩定值的時間快了0.03 s，加載后的調節時間也稍快于ADRC控制，但是不論起動、加載還是卸載后的跟蹤曲線都有很大的超調，不能滿足跟蹤精度要求高的系統。而ADRC控制系統不僅跟蹤快速，且沒有超調。

上述仿真驗證的是輸入信號為常值時控制系統跟隨性，圖8反映輸入為正弦變化的信號時系統的連續跟隨情況，在t=3 s時加入一個0.2 sint的擾動，觀察ADRC和PID控制系統的性能，圖9是實際擾動與觀測擾動曲線。

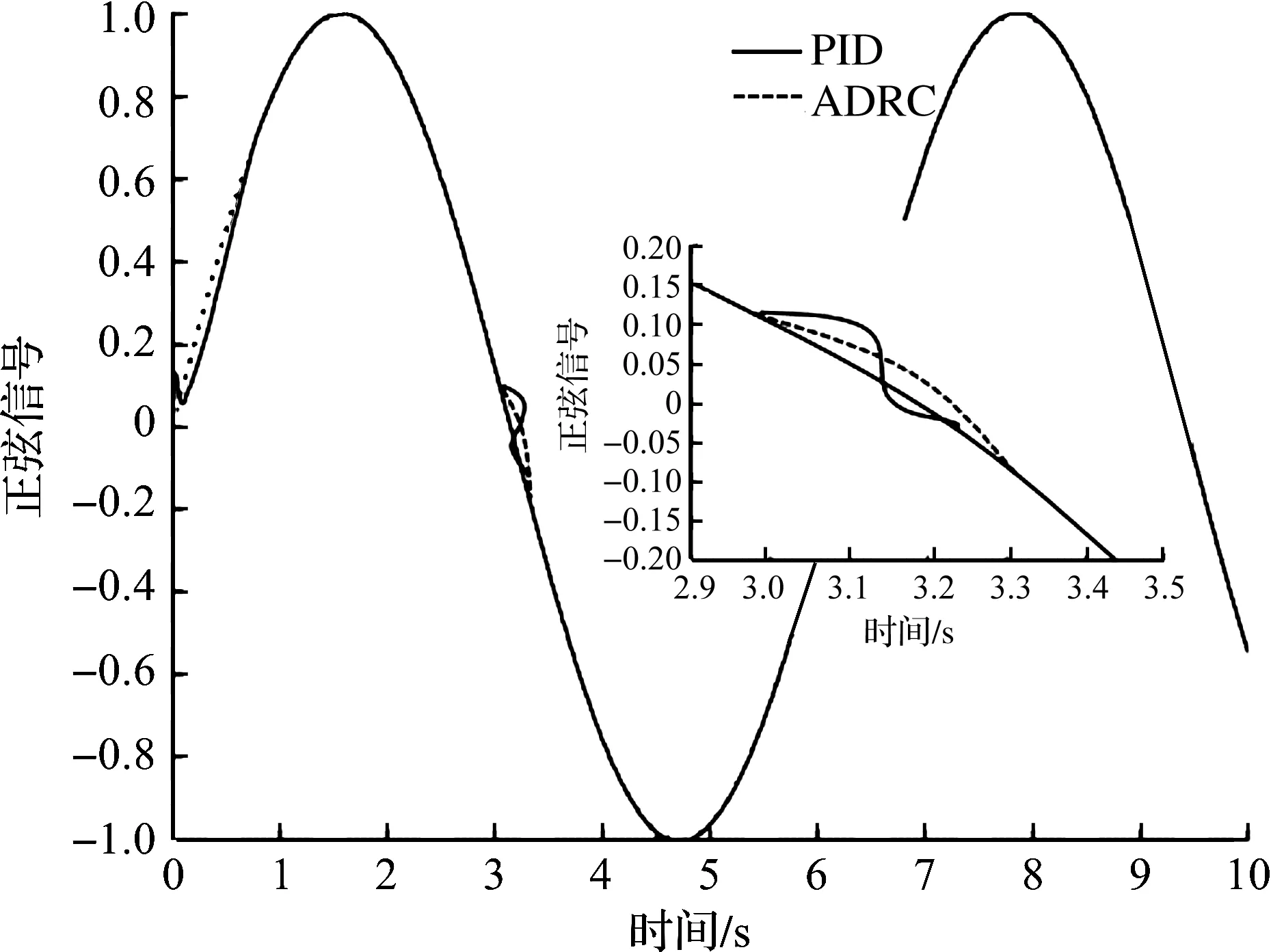
圖8 正弦信號下PID與ADRC控制系統抗干擾性能對比Fig.8 Comparison of anti-interference performance between PID and ADRC control system under sinusoidal signal

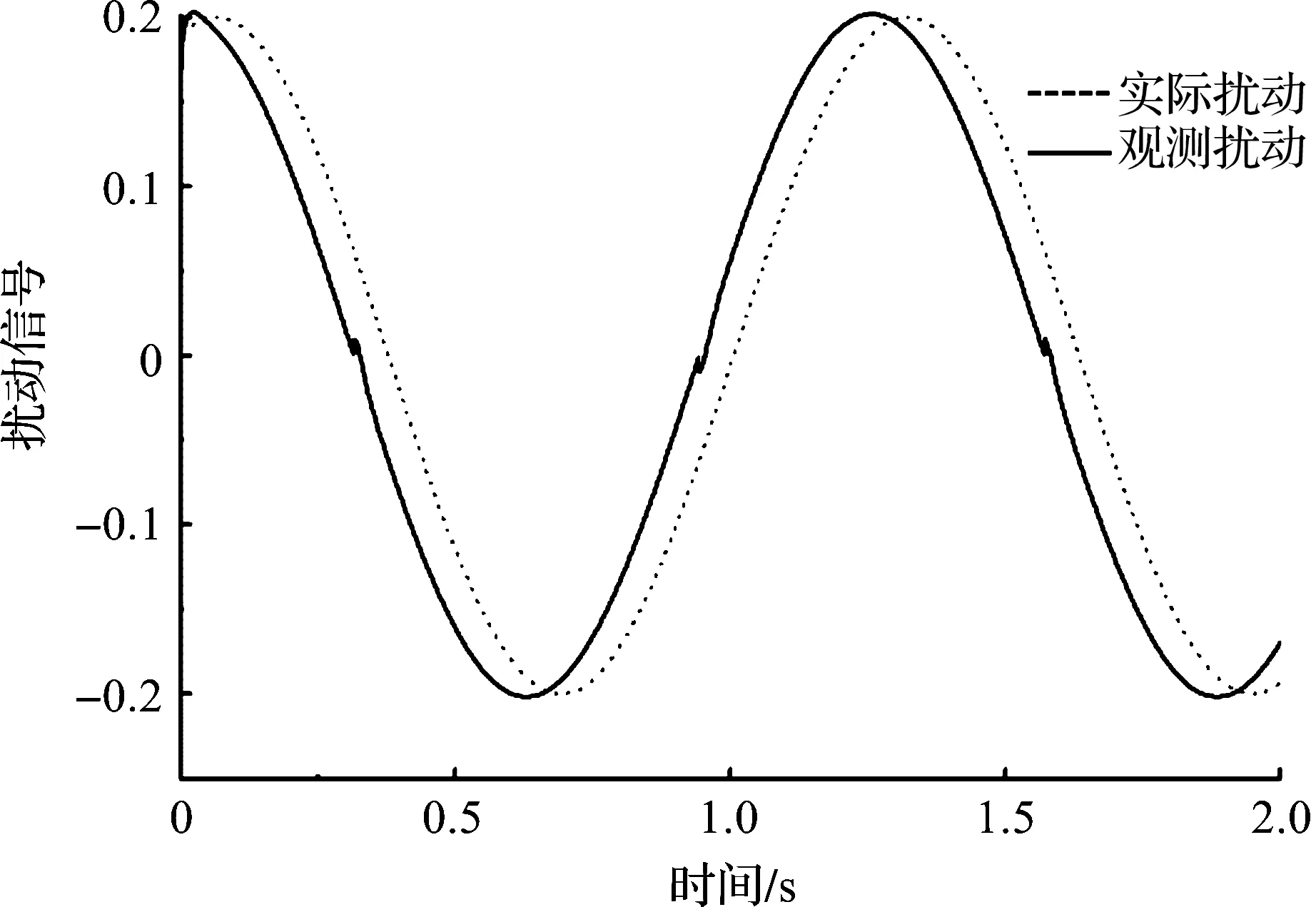
圖9 實際擾動與觀測擾動Fig.9 Actual disturbance and observation disturbance

從圖8可得：正弦信號下，起動時PID控制的穩定性低于ADRC控制，加入干擾信號后，兩者均能迅速恢復穩定跟蹤，但ADRC的跟蹤曲線比較平滑，抗干擾能力強，而PID控制的跟蹤曲線波動較大。

伺服電機控制的目標是實現電機無超調和快速響應，為了更有力驗證ADRC控制系統在負載擾動下的轉速和位置響應性能，搭建測試平臺結構如圖10所示，PMSM參數與仿真所用電機參數一致，以意法半導體公司的微控制器STM32F407ZGT6作為系統的主芯片，三相逆變器產生六路PWM波形驅動電機轉動，采用分辨率為2 048 ppr的增量式光電編碼器實現轉子位置檢測，使用測功機加載需要的負載擾動，并測出實驗所需的相關數據。系統采用id=0矢量控制，位置環和速度環采用ADRC控制器一體化控制，電流環采用PI控制器。

實驗分別作了2 個驗證：給定轉子位置為60°，360°，在t=1.5 s施加0.2 N·m的負載，分別得出PID和ADRC控制系統位置響應曲線；給定轉速為500，1 000 r/min，在t=1.5 s施加0.2 N·m的負載，得出PID和ADRC控制系統速度響應曲線。對于實驗中的數據取關鍵點進行曲線分析，如圖11，12所示。

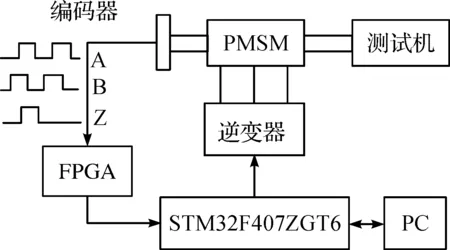
圖10 測試平臺結構圖Fig.10 Structure diagram of Test platform

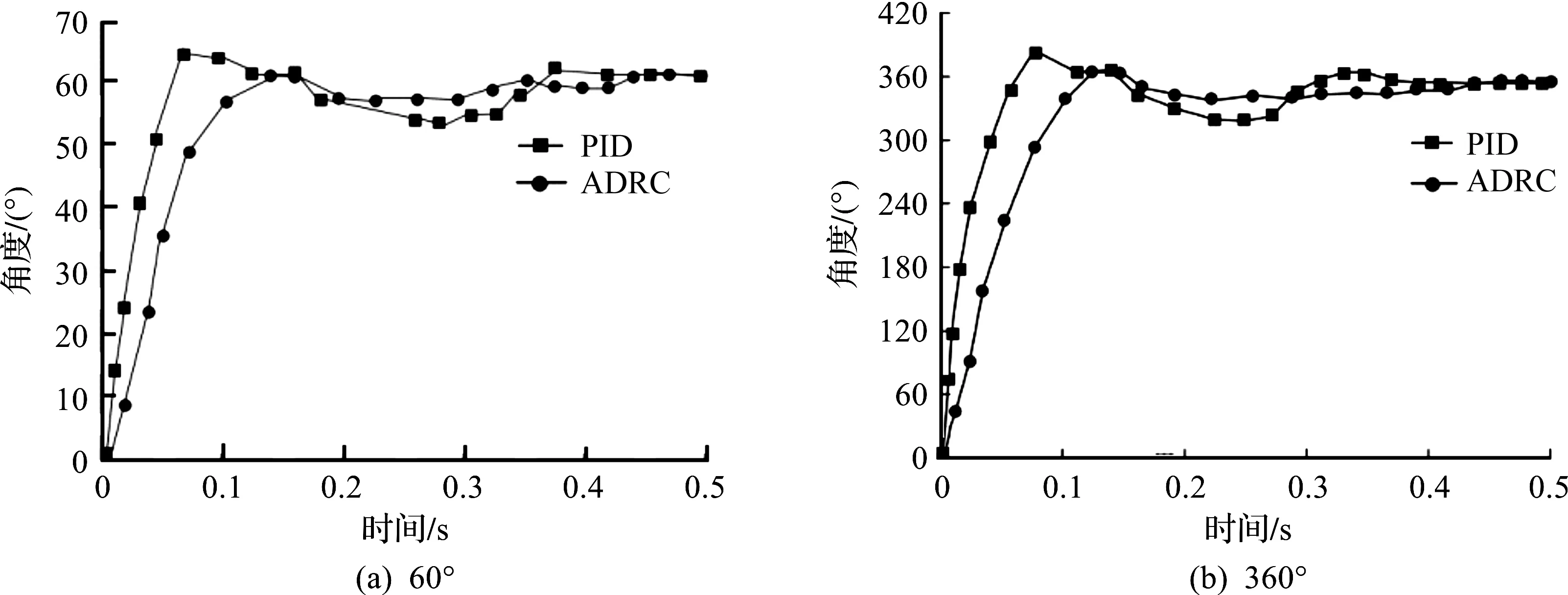
圖11 位置響應曲線Fig.11 Response curve of position

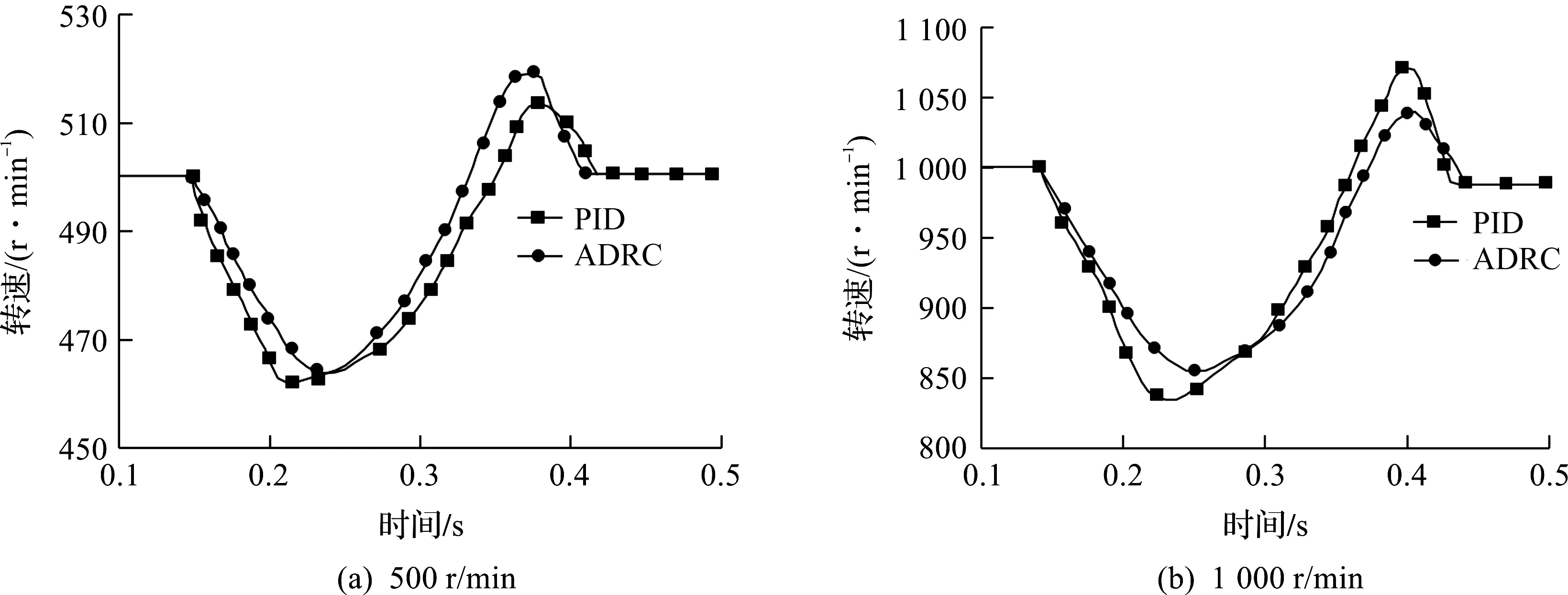
圖12 速度響應曲線Fig.12 Response curve of speed

由圖11可得：PID與ADRC均能實現快速響應，給定位置為60°時，PID控制和ADRC控制系統分別在0.419，0.426 s恢復穩定值；位置為360°時，PID和ADRC控制系統分別在0.423，0.431 s恢復穩定，但是PID控制存在很大的超調，曲線上下浮動大，ADRC控制系統比較穩定。

系統速度響應曲線如圖12所示，在加入負載擾動后，PID與ADRC均能快速穩定，給定速度為500 r/min時，PID和ADRC控制系統分別在0.396，0.401 s恢復穩定；給定速度為1 000 r/min時分別在0.417，0.421 s到達給定值。而PID控制曲線波動比ADRC控制曲線波動大，證明ADRC控制系統控制精度更高，這和仿真結果是一致的。

5 結論