基于故障率的艦艇維修備品備件優化配置*

張懷強，盧遠超，王 孟

（海軍工程大學，武漢 430033）

0 引言

現代海戰往往具有持續高強度的特點，對艦艇裝備保障率提出了較高的要求[1]。通過戰時備品備件資源的科學配置，提升艦艇裝備保障率，增強裝備可靠性，對保障艦艇執行高強度作戰任務具有重要意義。傳統的基于經驗的備品備件資源配置方案，雖然一定程度上保障了艦艇裝備的基本可用，但配置方式較為粗放，難以適應高強度作戰任務對于保障裝備可靠性的需求，迫切需要探索一種面向裝備保障率提升的艦艇維修備品備件資源優化配置方法。

本文針對上述問題，分析了不同備品備件故障率分布特點，建立艦艇裝備保障率計算模型和備品備件保障費用約束模型，并根據作戰任務特點進行多目標決策，對提升艦艇裝備保障率，增強裝備可靠性，保障艦艇作戰任務的執行具有重要意義。

1 多目標模糊決策的基本理論

多目標模糊決策是由哈佛大學Zadeh教授提出的“模糊優化”理論的發展和延伸[2]。其基本理論為，在多目標優化決策模型中，多個優化目標之間經常存在強烈的沖突，造成某些目標的優化結果不能盡如人意。通常情況下，為了緩和這種沖突、兼顧所有目標的利益，決策者可以根據實際決策環境，提前給每個目標函數設定一個期望值，每個目標期望值都要等于或劣于其目標函數在系統約束下的最優值，進而根據目標取值的上限和下限分別建立決策滿意度函數，并根據目標特點對滿意度函數賦以權重，求得總滿意度最高的決策方案[3]。

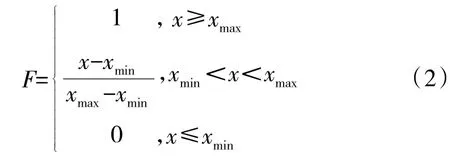
一般來說，優化目標分為最大化期望和最小化期望兩種，決策者對優化目標的滿意程度根據目標取值的上限和下限確定，最小化期望目標的滿意度計算公式為：

式中，F為決策者對優化目標的滿意度；x為優化目標值；xmax為目標優化上限；xmin為目標優化下限。

同理，最大化期望目標的滿意度計算公式為：

2 基于故障率分布的艦艇維修備品備件多目標模糊配置模型

2.1 艦艇裝備保障率計算模型

考慮到艦艇作戰的特殊環境，艦艇裝備維修通常實施換件維修，即當裝備出現故障時，不用對零件做處理，直接用備品備件代替故障件，以保障裝備的可靠性。裝備保障率是指在戰時，通過對艦艇裝備所需的備品備件進行更換，使裝備始終保持有效運行狀態的概率[4]。由此可見，艦艇裝備保障率的高低與其所攜帶的備品備件的壽命特點有關。通常情況下，備品備件可以分為指數分布壽命件、正態分布壽命件和威布爾分布壽命件。

2.1.1 指數分布壽命件平均失效概率計算

艦艇裝備中的指數分布壽命件通常是指具有恒定故障率的電子元器件，在損耗前正常使用的復雜部件或由于隨機高應力導致故障的部件，以及一些弱損耗部件也可以視為指數分布壽命件。

指數分布壽命件的失效概率密度函數f（t）可以表示為：

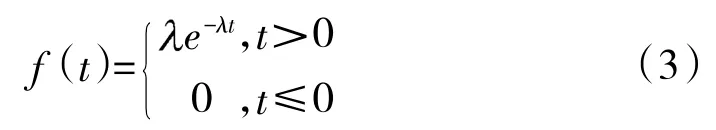
式中，t為指數分布壽命件工作時間；f（t）為指數分布壽命件失效概率密度；為分布參數，＞0。

指數分布壽命件的分布函數F（t）可以表示為：

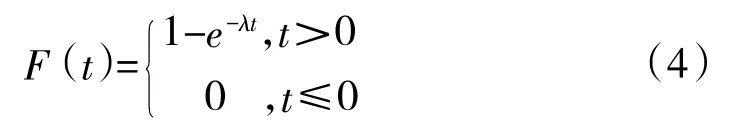
根據分布函數可知，指數分布壽命件隨著工作時間的增加，其失效概率遞增。對含有該類備品備件的艦艇裝備的維修保障過程中，通過增加指數分布壽命件的配置數量，在艦艇執行作戰任務時間一定的條件下，可以有效縮短單個指數分布壽命件的工作時間，進而降低裝備中該型備品備件的平均失效概率，提升裝備可靠性。

指數分布壽命件的平均失效概率與配置數量的關系可以表示為；

式中，x為指數分布壽命件的配置數量；T為艦艇任務執行時間；P（x）為指數分布壽命件平均失效概率。

2.1.2 正態分布壽命件平均失效概率計算

正態分布壽命件主要包括在平均壽命期集中損壞的一類備品備件，如輪胎、變壓器、燈泡、直升機旋翼葉片等。

正態分布壽命件的失效概率密度函數f（t）可以表示為：

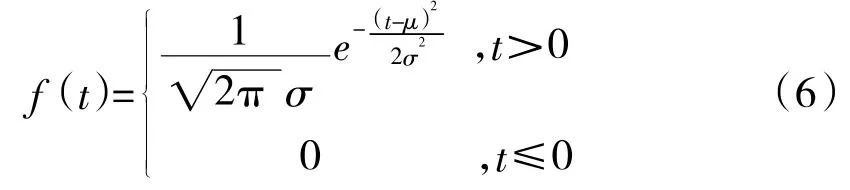
式中，t為正態分布壽命件工作時間；f（t）為正態分布壽命件失效概率密度；μ、σ為分布參數，σ＞0。

正態分布壽命件的分布函數F（t）可以表示為：

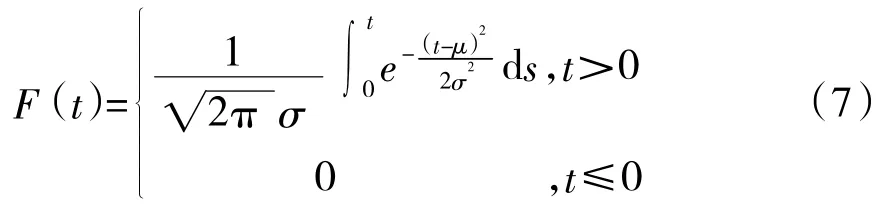
與指數分布壽命件類似，通過增加正態分布壽命件的配置數量，可以有效縮短單個正態分布壽命件的工作時間，進而降低裝備中該型備品備件的平均失效概率，提升裝備可靠性。

正態分布壽命件的平均失效概率與配置數量的關系可以表示為；

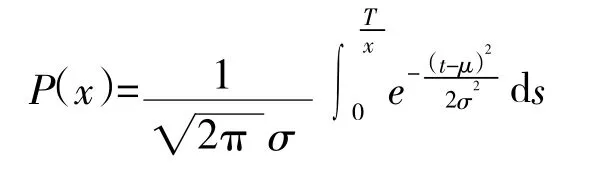
式中，x為正態分布壽命件的配置數量；T為艦艇任務執行時間；P（x）為正態分布壽命件平均失效概率。

2.1.3 威布爾分布壽命件平均失效概率計算

威布爾分布壽命件主要是指機電類產品的磨損累計失效形式，典型的威布爾分布備品備件包括滾動軸承、繼電器、陀螺、電動機、發動機、蓄電池、液壓泵、材料疲勞等[5]。

威布爾分布壽命件的失效概率密度函數f（t）可以表示為：

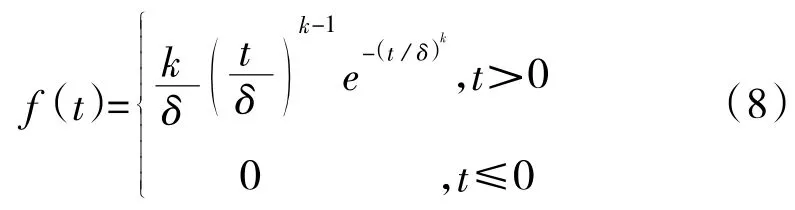
式中，t為威布爾分布壽命件工作時間；f（t）為威布爾分布壽命件失效概率密度；k、δ為分布參數，k，δ＞0。

威布爾分布壽命件的分布函數F（t）可以表示為：

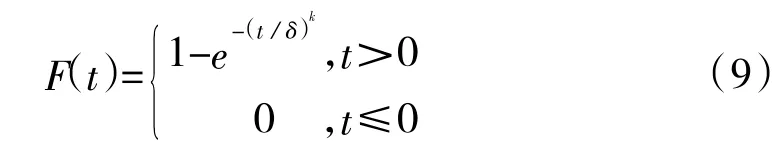
與指數分布壽命件類似，通過增加威布爾分布壽命件的配置數量，可以有效縮短單個威布爾分布壽命件的工作時間，進而降低裝備中該型備品備件的平均失效概率，提升裝備可靠性。

威布爾分布壽命件的平均失效概率與配置數量的關系可以表示為；

式中，x為威布爾分布壽命件的配置數量；T為艦艇任務執行時間；P（x）為威布爾分布壽命件平均失效概率。

2.1.4 含有多種備品備件的艦艇裝備保障率計算

通常情況下，一型艦艇裝備由多種不同壽命分布類型的備品備件組成，當其中任何一個備品備件失效時，則該艦艇裝備失效[6]。假設某一個艦艇裝備由m個相同類型的指數分布壽命件，n個相同類型的正態分布壽命件和q個相同類型的威布爾分布壽命件組成，則該艦艇裝備保障率與3種備品備件的配置數量x，y，z的關系可以表示為：

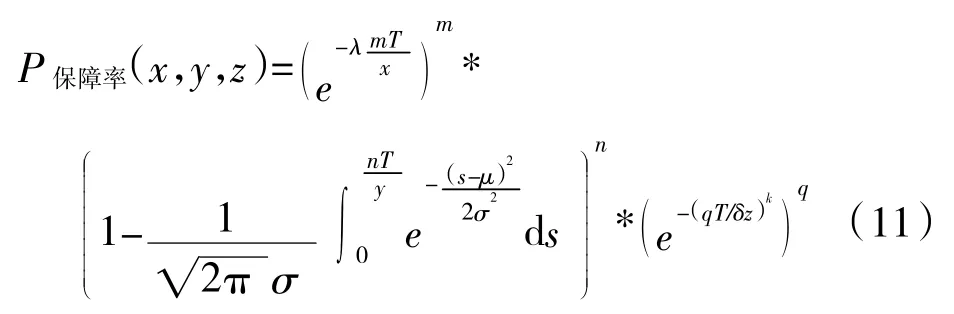
式中，x為指數分布壽命件的配置數量；y為正態分布壽命件的配置數量；z為威布爾分布壽命件的配置數量；T為艦艇任務執行時間；m為該艦艇裝備所含有的指數分布壽命件個數；n為該艦艇裝備所含有的正態分布壽命件個數；q為該艦艇裝備所含有的威布爾分布壽命件個數；λ，σ，μ，δ，k 為備品備件的分布參數，λ，σ，μ，δ，k＞0。

通過公式可以看出，艦艇裝備的保障率與保障該裝備的備品備件配置數量有關，隨著各型備品備件的配置數量增加，裝備中各備品備件組成單元的平均失效概率降低，艦艇裝備保障率隨之提升。

2.2 艦艇維修備品備件保障費用計算

戰場條件下，為了保障裝備的可靠性，艦艇編隊都會攜帶一定的備品備件，然而其數量并不是越多越好，備品備件攜行過多不僅會造成損失和浪費，大大增加戰時艦艇維修保障費用，而且還會占用大量的艦艇空間，限制艦艇綜合保障能力的提升[7]。因此，有必要根據備品備件配置數量與保障費用之間的關系，對備品備件資源配置進行約束。

艦艇維修備品備件保障費用主要由兩部分組成。一是為保障艦艇裝備維修所需配置的備品備件的訂購費用，不同類型的備件往往具有不同的訂購單價，隨著備件配置數量的增多，訂購費用呈現線性增長；二是由于備品備件配置數量不足造成的艦艇裝備停機而產生的損失費用，主要包括停機損失、維修或保障延遲所占用的費用等[8]。

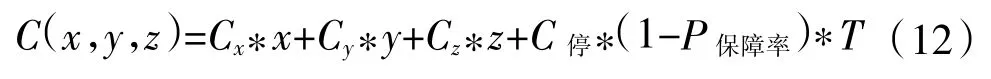
假設保障某一艦艇裝備的3種類型備品備件的配置數量分別為x，y，z，則備品備件保障費用的計算公式為：式中，x為保障該裝備的指數分布壽命件的配置數量；y為保障該裝備的正態分布壽命件的配置數量；z為保障該裝備的威布爾分布壽命件的配置數量；Cx為指數分布壽命件的單位訂購費用；Cy為正態分布壽命件的單位訂購費用；Cz為威布爾分布壽命件的單位訂購費用；C停為艦艇裝備停機損失費用；T為艦艇任務執行時間；P保障率為3種備件配置數量分別為x，y，z條件下的艦艇裝備保障率。

2.3 艦艇維修備品備件多目標模糊配置決策

戰場條件要求備品備件資源配置更多的面向艦艇裝備保障率的提升，同時備品備件配置數量也要滿足戰時保障費用約束[9]。這兩個因素通常是相互制約的：當要求更高裝備的保障率就意味著投入更大的保障費用，而減少保障費用時會使裝備的保障率無法達到要求[10]。一般情況下艦艇執行的作戰任務不同，目標權重往往不同，高強度、短時間的作戰任務要求更高的艦艇裝備保障率；相反，低強度、長時間作戰任務則對節約保障費用提出更高的要求。

根據艦艇執行作戰任務的特點不同，分別對艦艇裝備保障率和備品備件保障費用設立目標期望值，進而根據目標取值的上限和下限分別建立決策滿意度函數，對滿意度函數賦以權重，求得總滿意度最高的備品備件資源配置方案。

假設保障某一艦艇裝備的3種類型備品備件的配置數量分別為x，y，z，則戰時艦艇裝備保障率的滿意度函數表達式為：

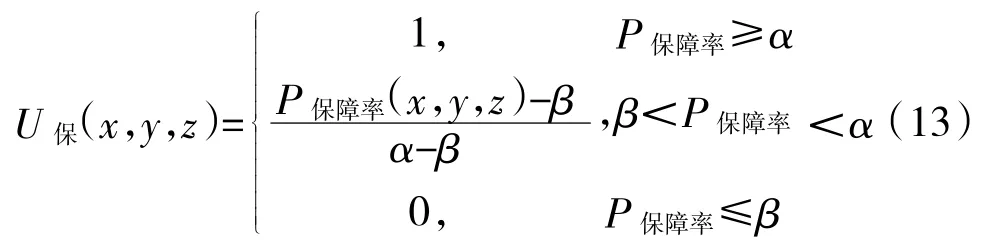
式中，U保為決策者對艦艇裝備保障率的滿意度；α為決策者對艦艇裝備保障率的滿意上限；β為決策者對艦艇裝備保障率的滿意下限；

假設保障某一艦艇裝備的3種類型備品備件的配置數量分別為x，y，z，則戰時備品備件保障費用的滿意度函數表達式為：

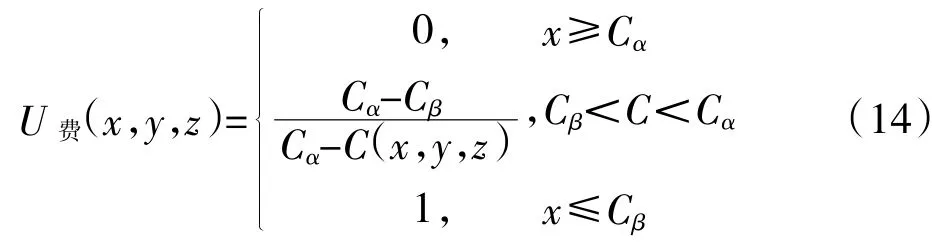
式中，U費為決策者對備品備件保障費用的滿意度；Cα為決策者對備品備件保障費用的滿意上限；Cβ為決策者對備品備件保障費用的滿意下限；

根據艦艇執行作戰任務的特點不同，分別對艦艇裝備保障率的滿意度函數和備品備件保障費用的滿意度函數賦予權重，進行加權求和，即為決策者總滿意度函數。

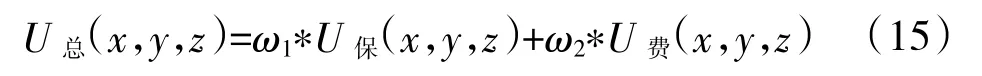
計算總滿意度最大時該艦艇裝備對應的3種類型備品備件的配置數量x，y，z，即為戰時備品備件資源的最優配置。運用本模型分別計算艦艇各裝備各型備品備件的配置數量并累加，得到該艘艦艇戰時的備品備件資源配置方案。

3 案例分析

執行某作戰任務艦艇的某一型艦艇裝備由4個可更換備品備件組成，其中包括2個相同類型的指數分布壽命件、1個正態分布壽命件和1個威布爾分布壽命件。根據同類型備品備件的歷史統計數據分析，指數分布壽命件的故障率參數λ=1/80 000 h，正態分布壽命件的平均壽命參數μ=2 400 h、標準差σ=200 h，威布爾分布壽命件的尺度參數δ=12 000 h、形狀參數k=2，3種備品備件的單價分別為Cx=20 000元、Cy=8 000元、Cz=40 000元，單位時間停機損失C停=1 000元/h，艦艇執行任務時間T=4 000 h。

根據上述分析，分別建立艦艇裝備保障率函數和備品備件保障費用函數。

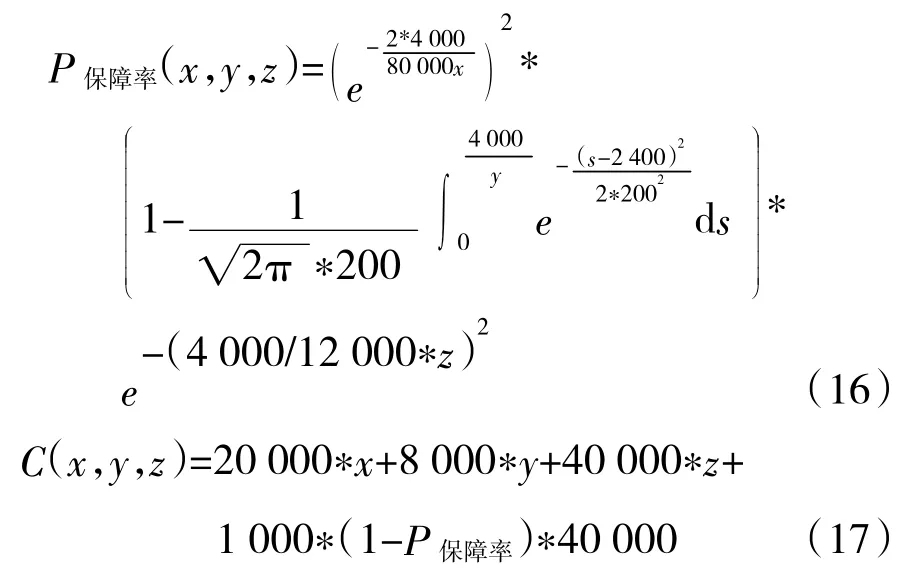
由于艦艇裝備保障率P保障率的取值范圍為0-1，以艦艇裝備保障率函數直接作為決策者的滿意度函數，即：

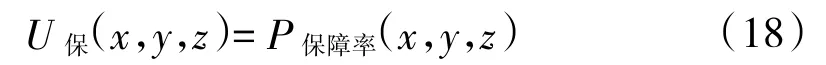
取備品備件保障費用滿意上限Cα=200萬元，滿意下限Cβ=20萬元，建立決策者對保障費用的滿意度函數。

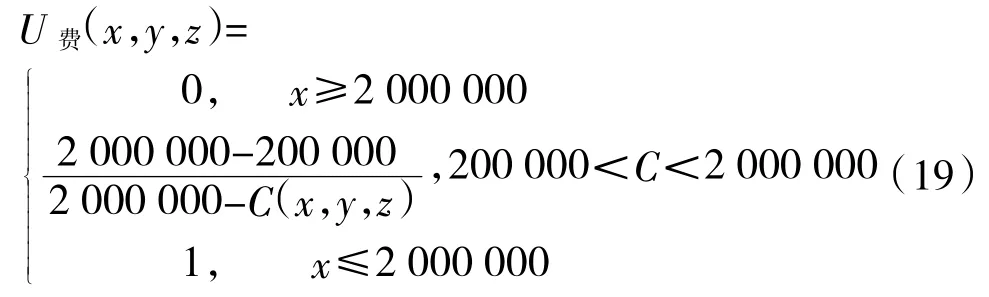
高強度、短時間任務要求提升艦艇裝備保障率的滿意度函數權重；相反的，低強度、長時間任務則要求備品備件保障費用的滿意度函數具有較大的權重。根據艦艇作戰任務特點，分別取ω保=0.9，ω費=0.1，得到艦艇維修備品備件資源配置的總滿意度函數。

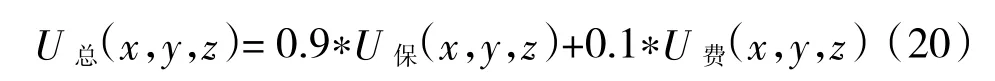
分別對x，y，z求偏導數，令偏導數等于零，求解總滿意度函數最大值。

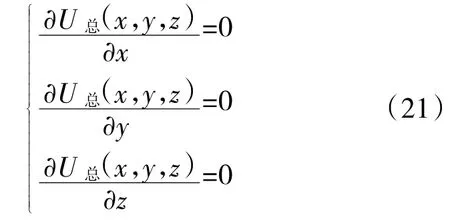
解方程可得，x=14.24，y=2.99，z=5.03，因此，保障該艦艇裝備的備品備件資源配置方案為：指數分布壽命件的配置數量為14個、正態分布壽命件的配置數量為3個、威布爾分布壽命件的配置數量為5個。根據模型的意義，當前配置方案滿足了戰時的維修保障費用約束，同時提升了裝備保障率，有效保障了該艦艇裝備作戰任務能力的發揮。

當前配置方案下的該艦艇裝備保障率和備品備件保障費用如表1所示。

表1 當前配置方案下的該艦艇裝備維修備品備件配置

4 結論

戰場條件對艦艇裝備維修保障提出了較高的要求，本文通過建立戰時艦艇維修備品備件資源配置多目標模糊配置模型，在維修保障費用約束下最大化提升裝備保障率，增強裝備可靠性，對于保障艦艇執行高強度作戰任務具有重要意義。