弱送端電網直流群同時換相失敗對電網功角穩定特性的影響研究

于燦平

（國電南京自動化股份有限公司， 南京 210032）

0 引言

近年來， 大容量特高壓直流輸電工程得到了快速發展， 國家電網公司相繼投產多條特高壓直流工程， 促進了我國西部和北部地區水電等清潔能源的快速消納。 同時， 我國電網也形成多直流送出、 多直流饋入格局， 且“強直弱交”的特征凸顯， 交直流系統故障影響范圍增大， 通過直流異步互聯的送、 受端電網均受到直流功率擾動的沖擊[1-4]， 給電網的安全穩定運行帶來嚴峻考驗。

含直流饋入的受端電網短路故障發生后， 易引起直流發生換相失敗， 造成直流功率瞬時中斷，給電網又帶來一次功率沖擊的影響。 特別是多回直流同時發生換相失敗后， 給電網帶來極大的能量沖擊， 可能引起交流薄弱斷面穩定破壞。目前，相關研究大多集中在交直流系統常規故障下的電網穩定特性分析[5-10]以及單回直流換相失敗對電網的影響分析方面[11-19]。 隨著受端電網直流饋入回數和容量的不斷增加， 多饋入直流同時換相失敗對電網的影響也引起了一些專家的關注[20-21]， 但關注點均集中在多回直流因三相永久性故障（以下簡稱“三永故障”）的一次換相失敗沖擊的影響， 對受端電網發生單相永久性故障（以下簡稱“單永故障”）引起的相繼兩回換相失敗的影響研究較少。

本文結合等值系統模型， 分析單永故障造成的多直流同時相繼換相失敗對送端電網穩定運行的影響， 結合送端電網實際區域振蕩模式著重研究受端電網不同重合閘整定時間對功率波動的作用機制， 探討適用于送端電網實際情況的重合閘優化措施， 并通過實際電網算例進行仿真驗證。

1 同送同受跨區直流格局概況

為促進清潔能源的合理消納， 我國水資源豐富的西南地區已相繼建成落點華東地區的復龍—奉賢（復奉）、 錦屏—同里（錦蘇）以及宜賓—金華（賓金）特高壓直流工程， 直流總容量達到21.6 GW， 且送、 受端直流落點電氣聯系緊密， 落點之間不存在電網的重要薄弱斷面， 形成典型的同送同受大容量跨區直流格局， 如圖1 所示。

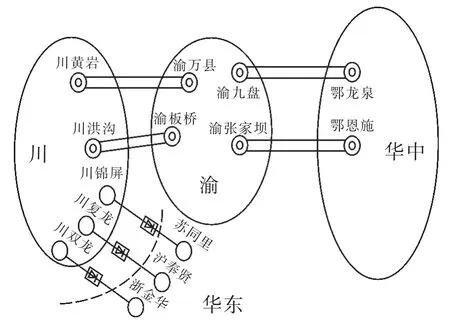
圖1 西南—華東地區同送同受跨區特高壓直流格局

四川電網位于送端電網末端， 承接賓金、 復奉以及錦蘇直流送端換流站所需電力， 通過黃巖—萬縣雙回500 kV 線路以及洪溝—板橋雙回500 kV 線路與重慶電網相聯， 重慶電網通過九盤—龍泉雙回500 kV 線路以及張家壩—恩施雙回500 kV 線路與湖北電網相聯， 華北—華中電網通過特高壓長南線相聯， 三回特高壓直流同時發生換相失敗故障后， 電網盈余功率先后沖擊渝鄂斷面以及特高壓長南線， 給電網的安全穩定運行帶來極大挑戰。

2 多回直流換相失敗對送端電網的影響

受端華東電網網架結構較強， 直流落點之間電氣距離較短， 華東電網發生短路故障易導致跨區特高壓直流發生同時換相失敗， 電網短路故障形態不同， 直流發生換相失敗次數也不同。 受端電網發生三永故障時， 由于系統僅存在一次短路沖擊， 往往造成直流同時一次換相失敗， 如圖2 所示； 受端電網發生單永故障時， 由于存在重合閘環節， 當故障線路重合于故障時又會為系統帶來二次短路沖擊， 進而再次引起直流發生換相失敗，造成直流發生相繼2 次換相失敗， 如圖3 所示。

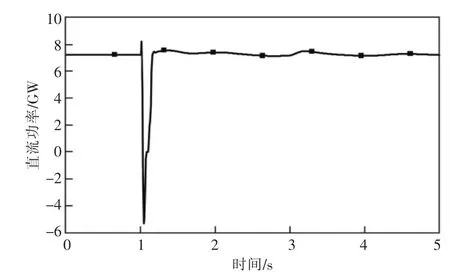
圖2 三大直流同時一次換相失敗后的直流功率曲線（錦蘇直流）

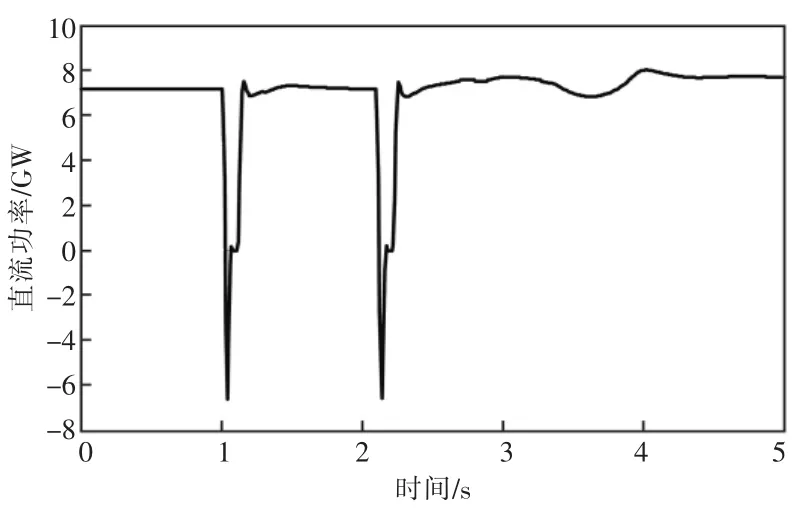
圖3 三大直流相繼兩次換相失敗后的直流功率曲線（錦蘇直流）

受端電網發生單永故障時， 三大特高壓直流相繼換相失敗后的渝鄂斷面功率波動幅值相較于三永故障下三大直流一次換相失敗后的渝鄂斷面功率波動幅值更大， 嚴重工況下更易引起渝鄂斷面失穩， 如圖4 所示。

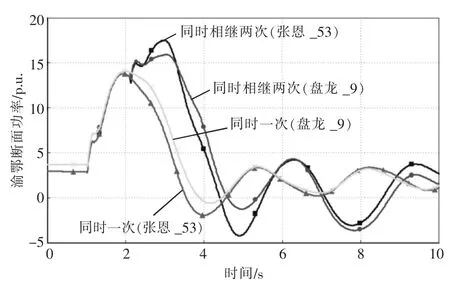
圖4 渝鄂斷面功率波動曲線

2.1 直流同時一次換相失敗對系統的影響

圖5 為交直流互聯系統等值模型。

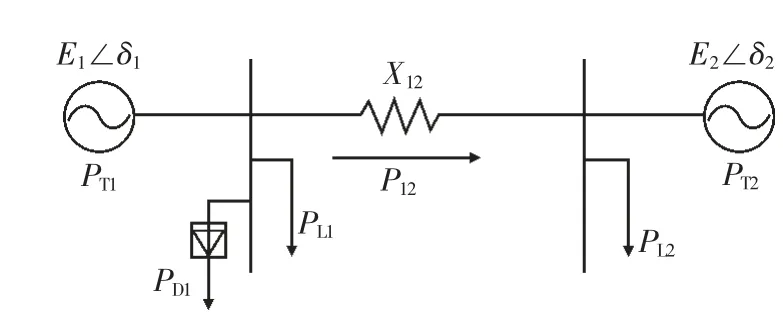
圖5 交直流互聯系統等值模型

忽略發電機內阻抗， 同步互聯等值系統發電機轉子運動方程可表示為：

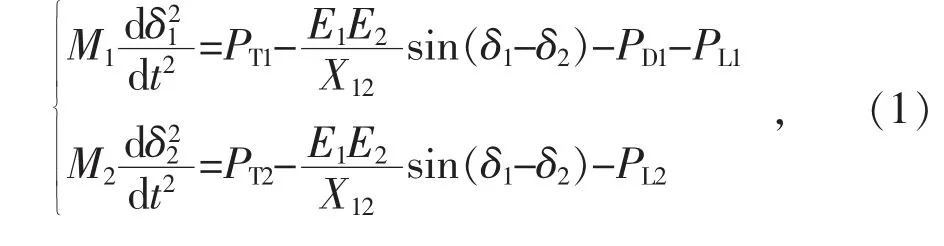
式中： M1， M2為等值系統慣量。

令等效功角δ=δ1-δ2， 可得：

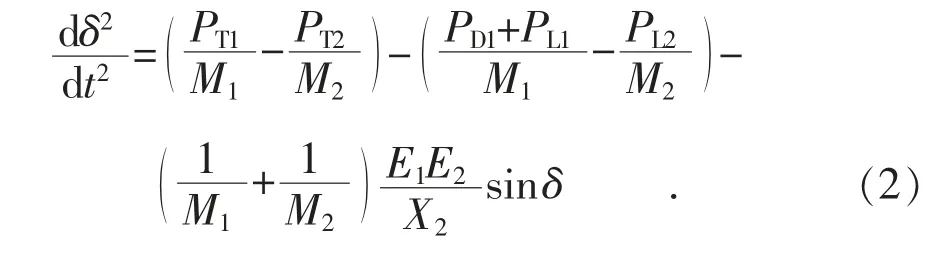
由式（2）可得到等效機械功率PT和等效電磁功率PE分別為：

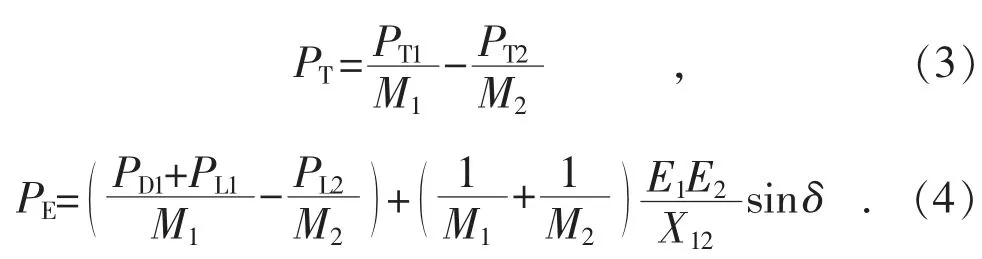
為簡化分析， 忽略發電機機械功率和內電勢的變化， 假定等效機械功率動態過程中保持不變， 由式（4）可知等效電磁功率將受到直流傳輸有功功率的影響， 式（2）變為：

由此可將兩機系統等效為單機系統， 相關特性可基于單機等面積定則進行探討分析。 直流發生一次換相失敗下的功率特性曲線如圖6 所示。正常運行時功率特性曲線為PI， δ0時刻直流發生換相失敗， 等效電磁功率瞬時下降， 功率特性曲線向下平移為PII。 由于機械功率大于電磁功率，機組加速， δC時刻故障清除， 直流功率恢復， 系統加速面積為Sabcd； 故障清除后， 等效發電機電磁功率大于機械功率， 系統開始減速， 減速面積為Sdefg。 評估直流一次換相失敗后系統的穩定性，需對系統加、 減速面積進行評估， 且受系統初始運行功率水平、 發生換相失敗的直流功率水平以及直流換相失敗持續時間影響。

從倫理學來看，中正、中行、中允（公正、公平）之道是人們所崇尚的高尚道德，也是社會主義價值觀的一個重要方面，即以公正、公平的立場和態度來處理人與人之間的關系，建設一個公平、正義的和諧社會。

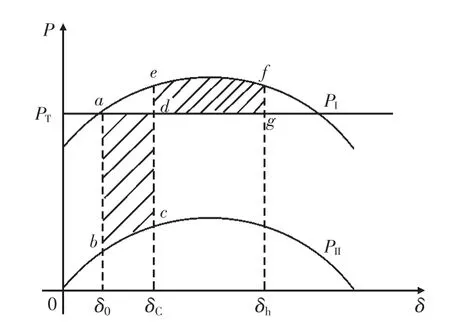
圖6 單次換相失敗下的功率特性曲線

2.2 直流相繼兩次換相失敗對系統的影響

基于單機等面積定則， 直流發生相繼兩次換相失敗下的功率特性曲線如圖7 所示。 正常運行時功率特性曲線為PI， 電網運行穩態工作點為a，δ0時刻直流發生換相失敗， 等效電磁功率瞬時下降， 功率特性曲線向下平移為PII。 由于機械功率大于電磁功率， 機組加速， 加速面積為Sabcd； δC時刻受端電網單相故障清除， 換相失敗結束， 直流功率恢復到正常水平， 功率特性曲線恢復至PI，機組減速， 減速面積為Sdefg； δr時刻， 受端電網單相重合閘啟動， 線路重合于故障， 導致直流再次發生換相失敗， 功率特性曲線再次降到PII， 機組再次加速， 加速面積為Sghij； δrc時刻受 端電網故障線路三相斷開， 故障清除， 功率特性曲線恢復至PI， 機組減速， 減速面積為Sjklm。 直流相繼換相失敗故障下， 系統總加速面積為Sabcd+Sghij， 總減速面積為Sdefg+Sjklm。 為分析系統相繼換相失敗故障對系統暫態穩定的影響， 需對上述加、 減速面積進行評估。

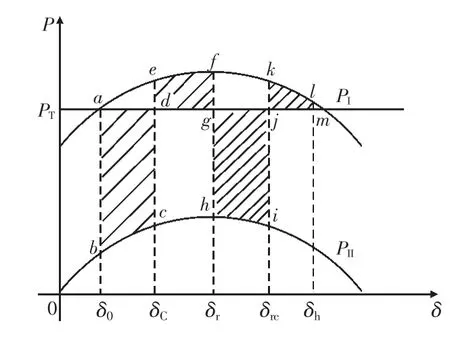
圖7 兩次換相失敗下的功率特性曲線

2.3 重合閘時間對交流斷面功率波動的影響

不同重合閘時間下， 特高壓直流同時相繼兩次換相失敗后， 斷面功率波動不同。 為分析重合閘時間對斷面功率波動大小的影響， 可將相繼兩次換相失敗看成是由兩個一次換相失敗線性疊加而成。 假設直流同時發生一次換相失敗的斷面功率波動曲線記為A：

式中： a 為功率振蕩幅值； ξ 為阻尼比； ω 為振蕩角頻率。

直流發生相繼兩次換相失敗后斷面的功率波動曲線記為B：

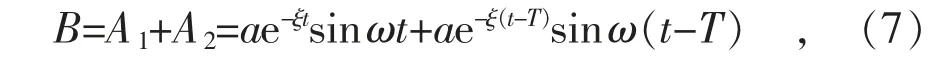
式中： A1， A2分別為2 次換相失敗的功率波動；T 為重合閘時間。

根據斷面兩邊電網震蕩模式的阻尼比和振蕩頻率套取ξ 和ω 值， 分析不同重合閘時間下線性耦合的功率振蕩疊加曲線， 如圖8 所示。

通過線性疊加后的功率振蕩曲線可以看出，相繼兩次換相失敗所引起的功率波動幅值較單次換相失敗故障大， 但隨著重合閘時間的不斷延長， 功率波動幅值不斷減小。

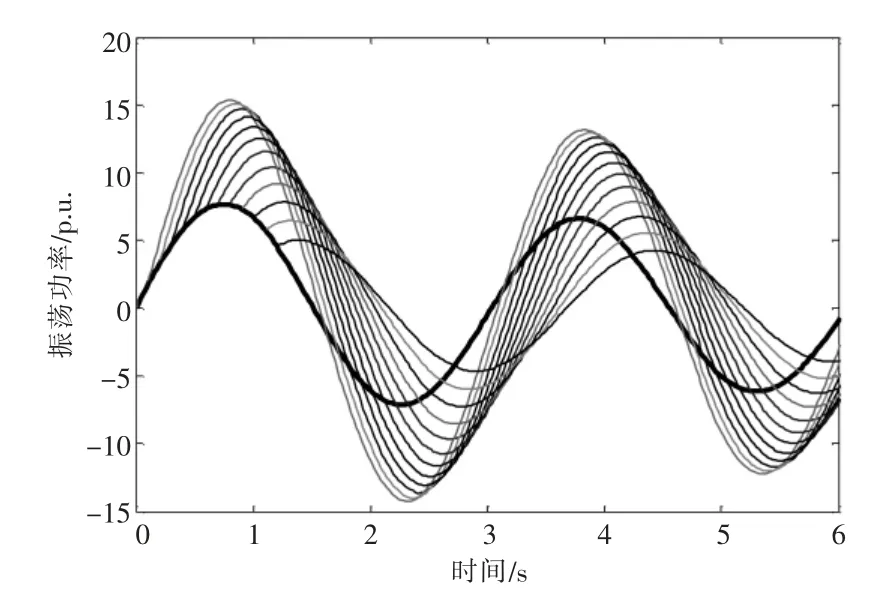
圖8 不同重合閘時間下的功率振蕩疊加曲線

3 受端電網單相重合閘整定時間優化

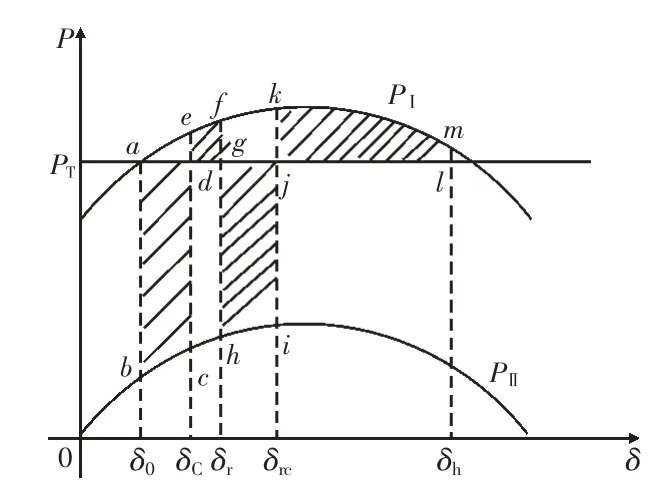
圖9 兩次換相失敗下的功率特性曲線（短重合閘時間）

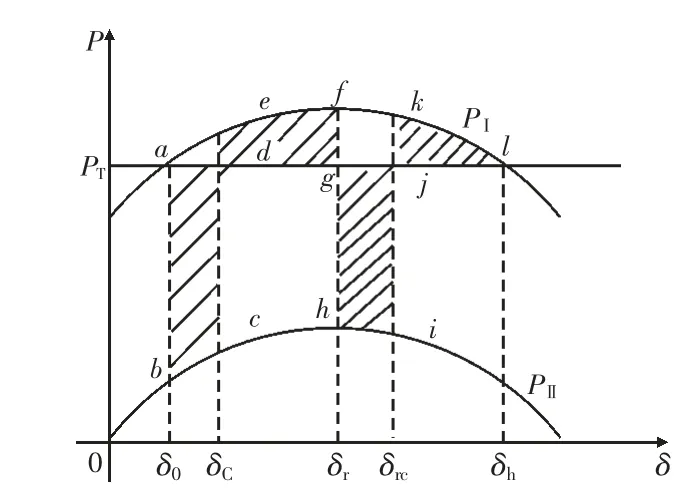
圖10 兩次換相失敗下的功率特性曲線（臨界穩定）

當三大直流發生第二次換相失敗時刻δr位于第一次換相失敗發生后機組功角回擺加速面積過程中， 如圖11 所示， 則直流第二次換相失敗對 系 統 所 造成 的加速 面積Sd′c′b′a′需 先 削 弱 回 擺 過程中的加速面積Sg′f′e′d′， 再驅動電網機組加速， 因此第二次換相失敗由于受到回擺加速面積的影響較第一次換相失敗對系統沖擊減弱； 反之若第二次換相失敗時刻δr位于回擺后再次加速過程中，第二次換相失敗較第一次換相失敗對系統的沖擊增強。 若繼續延長重合閘時間， 極端情況下等第一次換相失敗沖擊平息后， 再次發生換相失敗，對系統來說相當于承受兩個直流一次換相失敗的影響， 系統能夠維持穩定運行。

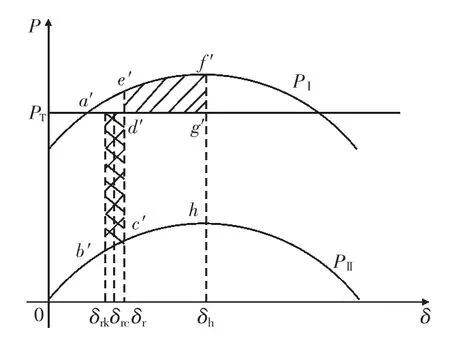
圖11 功角回擺過程中換相失敗下的功率特性曲線

由上述分析可知， 重合閘整定時間主要決定第二次換相失敗與第一次換相失敗沖擊后系統的暫態變化過程的耦合作用的大小。 兩次換相失敗對系統加、 減速面積變化過程的影響主要包括兩個方面： 一是電網主要振蕩模式決定系統功角搖擺周期， 重合閘時間對耦合作用的影響主要體現在第二次換相失敗發生在何種系統功角擺動的狀態下； 二是影響加、 減速面積大小的因素主要為電網初始運行方式、 運行點a 的位置、 兩區域的穩定裕度等， 系統暫態穩定裕度越高， 重合閘時間整定裕度也就越大。

4 算例驗證

選用某交直流混聯電網作為仿真算例， 其結構如圖12 所示， 其中A 電網和B 電網通過1 000 kV 特高壓線路互聯， 3 回特高壓直流均起始于C電網， 并饋入同一受端電網， 電網C 通過多回500 kV 線路與電網B 相連。方式安排特高壓線北送1 000 MW， C 電網外送B 電網1 450 MW， 仿真工具采用PSD-BPA 潮流、 暫態仿真程序， 即發電機采用考慮阻尼繞組的次暫態電勢變化的詳細模型， 并計及勵磁、 PSS（電力系統靜態穩定器）和調速系統， 且絕大部分機組的勵磁和PSS 為實測模型參數； 直流模型采用準穩態模型； 電網負荷采用恒阻抗加電動機的模型。

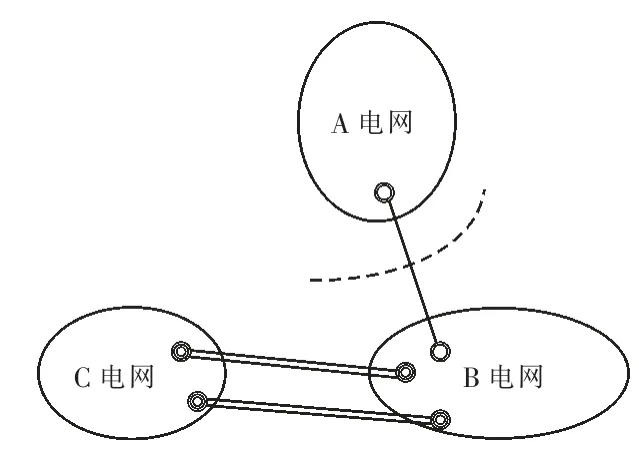
圖12 互聯電網結構

對A-B-C 互聯電網進行小干擾分析， C 電網對B 電網振蕩模式頻率約為0.33 Hz， 振蕩周期約為3 s。 調整直流饋入的受端電網單永故障重合閘整定時間， 不同重合閘時間下A-B-C 互聯電網的穩定情況如表1 所示。

由表1 可以看出， 直流饋入受端電網重合閘時間越短， A-B-C 互聯電網穩定性越差， 且隨著重合閘時間的不斷增加， A-B-C 互聯電網的穩定性逐漸提高。 其中， 當重合閘時間0.3 s 時， 三回特高壓直流同時相繼兩次換相失敗故障下， 造成BC 斷面和特高壓線失穩， 如圖13—15 所示。延長重合閘時間至0.5 s 或0.7 s 時， BC 斷面能夠保持穩定運行， 但仍造成特高壓線失穩。 當重合閘時間延長至0.9 s 后， A-B-C 互聯電網能夠保持穩定運行。 仿真結果與理論分析結論一致。

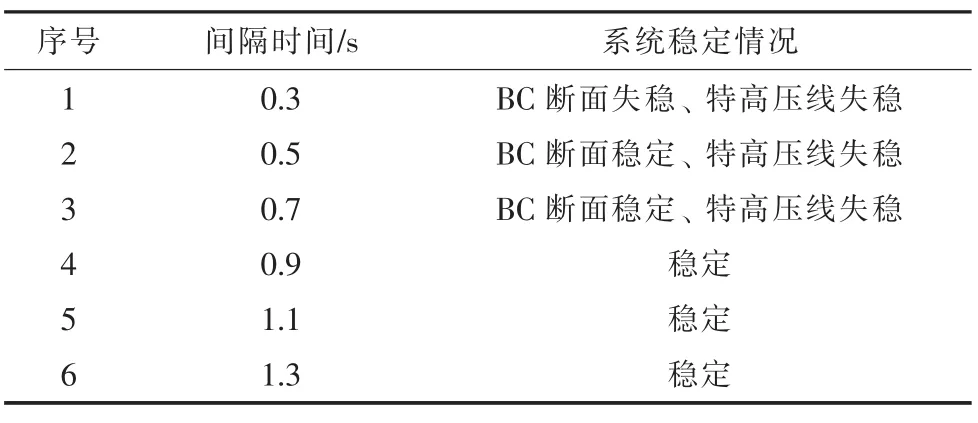
表1 不同重合閘時間下A-B-C 互聯電網的穩定情況

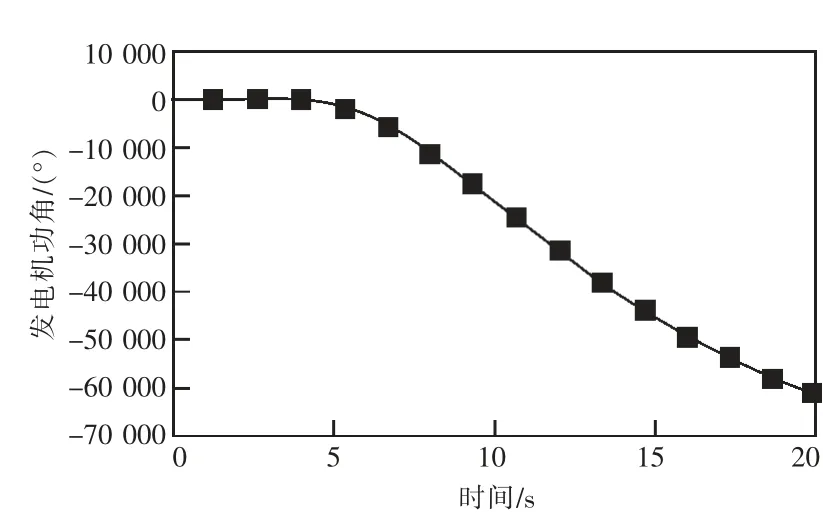
圖13 B-C 互聯電網的發電機功角曲線

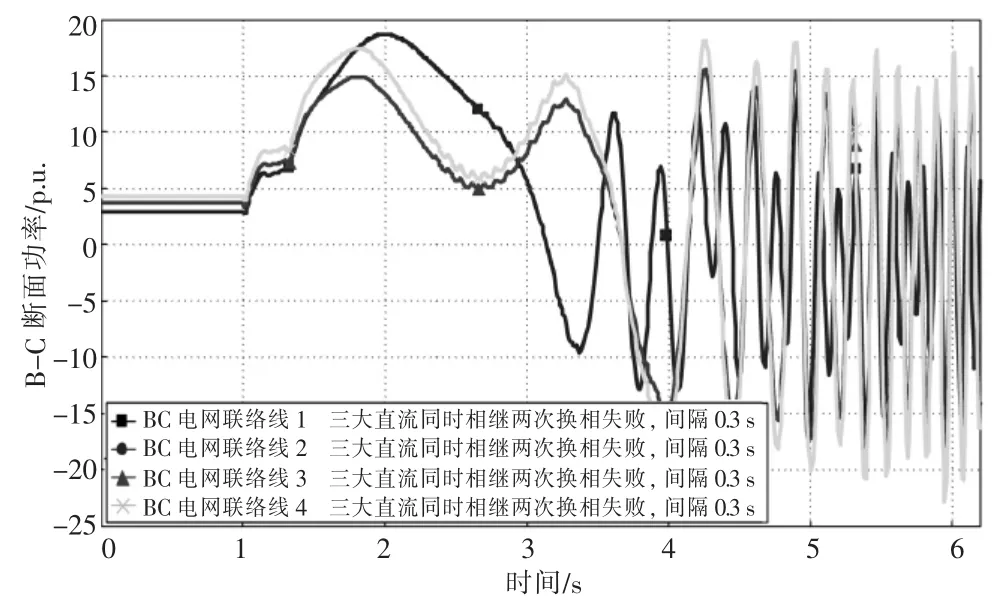
圖14 BC 斷面功率曲線

當重合閘時間延長超過0.5 s， 不同重合閘時間下B-C 互聯電網功角曲線如圖16 所示， 隨著重合閘時間的延長， 發電機功角擺開幅度逐漸減小， 當重合閘時間超過0.9 s 后， 第二次換相失敗發生時刻位于發電機功角回擺過程中， 此時互聯電網穩定性得到顯著提高， BC 斷面以及特高壓線能夠維持穩定運行。 仿真結果與理論分析結論一致。

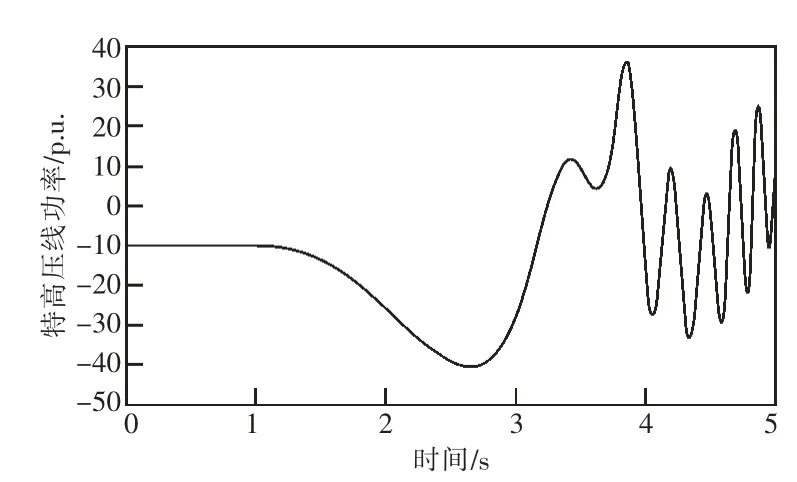
圖15 特高壓線功率曲線

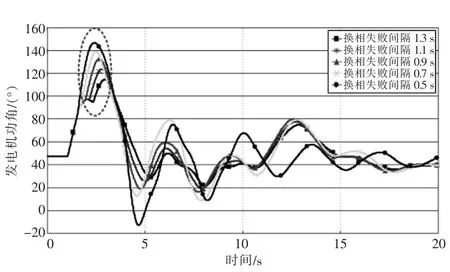
圖16 不同重合閘時間下B-C 互聯電網的發電機功角曲線

為充分反映三回特高壓直流同時相繼兩次換相失敗故障后聯絡斷面的功率波動情況， 考慮到BC 斷面為換相失敗后盈余功率沖擊的第一個主要薄弱斷面， 以BC 斷面為研究對象， 不同重合閘時間下BC 斷面功率波動曲線如圖17 所示， 功率波動幅值如表2 所示。

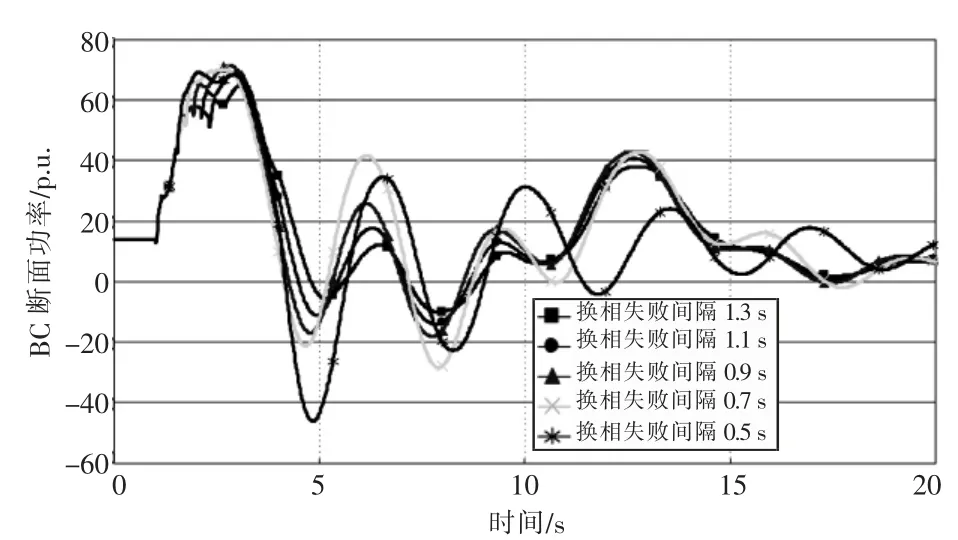
圖17 不同重合閘時間下BC 斷面功率波動曲線

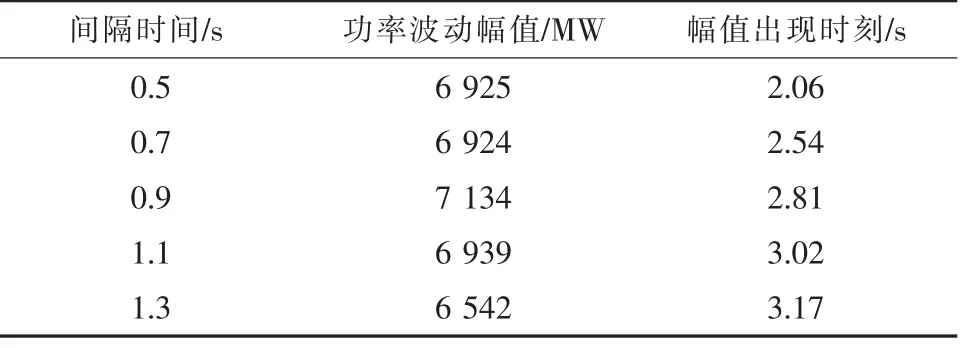
表2 不同重合閘時間下BC 斷面功率波動幅值

通過分析BC 斷面功率波動情況， 由于重合閘時間0.5 s 以及0.7 s 時， 特高壓線失穩， 電網發生較大變化， BC 斷面功率波動幅值受影響較大， 因此僅對比重合閘時間大于0.9 s 的BC 斷面功率波動幅值。 由表2 可知隨著重合閘時間的延長， BC 斷面功率波動幅值不斷減小， 與理論分析結論一致。

5 結語

受端電網單永故障易引起多回直流同時相繼兩次換相失敗， 對送端電網相關薄弱斷面造成較大沖擊， 引起斷面功率大幅振蕩， 影響送端電網的穩定運行。 本文通過機理分析和實際電網算例仿真， 驗證了延長單永故障重合閘時間可顯著減小系統的加速面積， 提高電網的穩定性， 同時也可降低相關斷面功率波動幅值。

優化重合閘整定時間的效果主要與送端電網振蕩頻率強相關， 而延長重合閘整定時間將造成受端電網長時間處于非全相運行狀態， 容易引起其他繼電保護裝置誤動作， 不利于受端電網的穩定運行。 實際運行中需綜合考慮送、 受端電網不同因素之間的相互影響， 以提高重合閘整定時間的優化效果。

本文基于單機等面積定則， 將系統運行條件進行了適當簡化和等效， 僅適用于分析受端電網故障造成的區域遠方送端電網功率沖擊影響。 上述范圍在一定程度上可不考慮系統網架結構變化以及復雜振蕩模式的影響。 因此， 本文分析方法不適用于送端電網故障或是難以引起主要典型振蕩模式的其他故障所造成的系統穩定問題。