基于PLSR建模的地鐵車站客流與周邊用地關系分析

馬超群，潘 杰，2，王 云

(1.長安大學 公路學院， 西安 710064; 2.南京市城市與交通規劃設計研究院股份有限公司， 南京 210000)

交通與土地利用之間有著不可分割的關系。通常，交通設施的建設使得兩地間或區域的可達性提高，人們愿意在交通設施附近或沿線購買房屋、建立公司或廠房，從而拉動土地利用的發展。同時，不同土地的利用形態又會要求和促進交通吸引產生量。長期以來，城市軌道交通規劃的目標制定、方案設計和評價都體現了滿足客運交通需求的理念，解決城市交通問題是城市軌道交通規劃的核心所在。對于軌道交通沿線的用地形態和軌道交通客運量之間的內部聯系，定性分析的研究較多，定量探討的研究較少。因此，對城市軌道交通站點周邊的土地利用形態與軌道交通客運量之間的關系建立模型，探討其內部聯系，具有重要的理論與現實意義。

美國亞利桑那州大學的Carol.M[1]采用TOD模式下的站點范圍400～600 m，以鳳凰城為例，研究輕軌對站點范圍內都市交通、用地等的影響。Robert[2]認為軌道交通站點的土地利用密度、開發情況、多樣程度，對軌道交通發展有著重要影響。Sumeeta[3]利用GIS研究了土地利用變化及其與城市軌道交通的關系，并分別從區域范圍和局部范圍建立了反映二者關系的模型。肖為周等[4]就軌道交通沿線土地利用變化對其客運需求的影響進行分析研究，對軌道交通沿線土地利用優化前后進行對比，分析優化用地對客運需求的影響，但僅從定性的角度對比分析，缺乏定量的計算分析。彭沙沙等[5]就軌道交通及土地利用協調發展方面，通過研究協調評價系統，有助于軌道交通線網合理規劃和沿線土地合理開發。王淑偉等[6]就站點周邊用地特性對軌道客流影響機理研究進行了線性分析，但是站點周邊的用地內部存在相關性，而單純的線性回歸難以準確描述其內部聯系。楊明等[7]就城市土地利用與交通需求之間的相互作用關系，研究了建立兩步式土地利用與交通需求相關關系模型的方法。楊敏等[8]針對新建城區的特點引入區位因子，考慮人口和土地利用與交通生成的關系建立預測模型。

針對上述問題，本文利用PLSR方法建立土地利用形態和客流量間的關系模型，解決各種土地利用形態間的多重共線性問題，得到精度較高的回歸模型，用于車站客流的測算估計。

1 PLSR建模基本原理

1.1 基本原理

偏最小二乘回歸法(partial least squares regression,PLSR)是一種多因變量對多自變量的回歸建模方法[9]。在普通的最小二乘回歸的應用中，當自變量和因變量之間存在多重相關性時，將會嚴重危害參數估計，擴大模型誤差，并破壞模型的魯棒性。這是因為在最小二乘法下，回歸系數的估計值是：A=(X′X)-1X′Y，當X中的變量完全相關時，(X′X)是不可逆矩陣，回歸系數將無法求得；而當X中的變量存在高度相關關系時，行列式|X′X|的值接近于零，回歸系數容易受較大舍入誤差的影響，甚至出現與實際情況相悖的結果。PLSR方法則不直接考慮因變量總體與自變量總體的回歸建模，而是在自變量的系統中提取了若干的對系統具有最佳解釋能力的新的綜合變量，然后在此基礎上，利用它們進行回歸建模。PLSR集多元線性回歸分析、典型相關分析和主成分分析的特點，較好地解決了變量之間存在多重相關性或樣本點數過少的回歸難題。

1.2 多因變量偏最小二乘回歸模型

多因變量最小二乘回歸是多個因變量對多個自變量建立的回歸模型[10]。設有q個因變量Y=(Y1,Y2,…,Yq)和p個自變量X=(X1,X2,…,Xp)。多變量PLSR的目的是尋找一個成分集合，用它對所有的因變量Y建立一個好的線性模型。模型如下：

k=1,…,q

(1)

式中：Ti被稱為潛在變量或成分，每個成分T1,…,Th都是自變量X的線性組合。對模型中的每個因變量Yk都有相同的成分T1,…,Th，只是它們的回歸系數不同。

假設對因變量Y=(Y1,Y2,…,Yq)和自變量X=(X1,X2,…,Xp)觀測了n組數據，記為：

它們的均值分別為：

對Y和X做中心化處理。經中心化處理后的數據矩陣分別記為：

F0=(F01,F02,…,F0q)

E0=(E01,E02,…,E0p)

其中l為n維單位向量。

此處，成分Ti按如下步驟確定：

2) 通過迭代確定其余成分。假設已經確定了Ti，E(i-1)j，F(i-1)k，以及相應的樣本值ti，e(i-1)j，f(i-1)k，現確定成分Ti+1。首先確定Eij，Fik。Eij為當E(i-1)j對Ti做回歸時的殘差，Fik是當F(i-1)k對Ti做回歸時的殘差，即：

(2)

ui+1=Fici+1

(3)

再使用單因變量PLSR方法，由ui+1，e01，…，e0p來構造成分Ti+1。

在成分Ti，…，Th都被確定后，利用式(1)對每個變量Yk建立回歸模型，參數β可使用普通最小二乘法估計。

1.3 模型的檢驗

用變量投影重要性指標來度量，自變量X對因變量Y的解釋能力，也就是各土地利用形態指標Xj對地鐵客流產生量Y的貢獻大小。

(4)

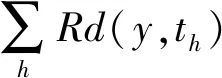
2 基于PLSR軌道交通車站客流模型

2.1 變量選取

2.1.1因變量選取

2.1.2自變量選取

自變量是能夠對軌道交通車站進出站客流量產生影響的因素。相關研究已經表明，混合用地能在很大程度上影響軌道站點的乘降客流量。考慮軌道交通車站周圍用地的復雜性，現有研究中應用較為廣泛的混合用地指標，其最重要的影響因素即熵指數(社區內用地類型的多樣性)，因此選取居住用地(X1，m2)、行政辦公用地(X2，m2)、商業金融用地(X3，m2)、文化娛樂用地(X4，m2)、醫療衛生用地(X5，m2)、教育科研用地(X6，m2)、公共綠地(X7，m2)、市政用地(X8，m2)、停車場(X9，m2)、文物古跡(X10，m2)10個表征用地性質的指標和建筑容積率(X11)、建筑密度(X12)2個表征用地開發強度的指標，共12個自變量[11]。

2.2 模型標定

2.2.1數據獲取

本文以西安市已運營的部分地鐵車站為樣本，選用了玉祥門、五路口、安遠門、會展中心、開遠門、鐘樓、大雁塔、青龍寺、太白南路、北大街、小寨、通化門等12個車站。利用各車站的AFC數據進行統計分析，得到每個車站任何時段內的進站客流與出站客流。通過ArcGIS對西安市用地現狀圖進行處理，得到車站800 m半徑范圍內的用地指標。

2.2.2相關關系系數

通過數據相關性分析，得到地鐵車站客流和12個影響因素之間的相關系數，見表1。可以看出，各變量間存在嚴重的多重相關性，如商業金融用地與建筑容積率，商業金融用地與建筑面積，相關性分別達到0.75，0.79。用方差膨脹因子法進行診斷，也可獲得同樣的結果[12]。

表1 變量間相關關系

2.2.3偏最小二乘回歸方程的確定

利用Matlab軟件，對自變量和因變量進行多因變量偏最小二乘回歸分析，得到車站客流與12個自變量的標準化偏最小二乘回歸模型。

按照標準化的逆過程，將偏最小二乘回歸方程進行還原，得到全日集散量：

[18]Wenzhou,which is to say almost everyone in Wenzhou,has a horror story about the financial crisis that struck in mid-2011.（2016-06-11）

Y1=-77 607+0.050X1+0.004X2+0.052X3+

0.001X4-0.021X5+0.010X6+0.016X7+

0.139X8-0.279X9-0.003X10+

38 477X11+61 796X12

早高峰進站客流量：

Y2=647.63+0.001X1+0.017 7X2-0.007X3-

0.001X4-0.001X5-0.000 5X6-

0.000 5X7+0.001X8+0.028X9+

0.002X10+322.86X11+ 858.08X12

早高峰出站客流量：

Y3=-6 360.3+0.003X1+0.002X2+

0.005X3+0.0003X4-0.000 5X5+

0.000 2X6+0.000 2X7+

0.012X8-0.019X9-0.000 1X10+

2 974.8X11+4 823.1X12

晚高峰進站客流量：

Y4=-3 930.8+0.002X1+0.001X2+

0.003X3-0.000 09X4-0.000 3X5+

0.000 02X6+0.000 3X7+

0.012X8-0.012X9-0.000 2X10+

2 022.6X11+3 328.5X12

晚高峰出站客流量：

Y5=-2 630.5+0.002X1-0.003X2+

0.000 7X3-0.000 2X4-0.002X5+

0.001X6+0.002X7+0.001X8-

0.016X9-0.000 3X10+

1 735.1X11+2 699.7X12

表2 模型的標準化系數

自變量全日集散量早高峰進站客流量早高峰出站客流量晚高峰進站客流量晚高峰出站客流量X10.1810.2430.1440.1550.256X 20.011-0.6790.0760.044-0.203X 30.207-0.2260.2330.2240.070X 40.007-0.2170.01980.008-0.033X 5-0.067-0.067-0.020-0.018-0.212X 60.067-0.1320.0160.0020.229X 70.0890.3590.0180.0300.306X 80.0580.4690.0620.0900.019X 9-0.0510.019-0.040-0.037-0.076X 10-0.017-0.202-0.008-0.019-0.037X 110.3860.1250.3440.3480.433X 120.3630.1960.3270.3350.395

3 模型分析與應用

3.1 車站全日集散量模型分析

根據式(4)計算變量投影重要性指標，計算結果如表3所示，數值的大小反映了變量對全日集散量的影響程度。投影變量重要性指標正負反映的是正相關影響和負相關影響。建筑容積率、建筑密度、商業金融、居住用地的變量投影重要性指標絕對值均超過1，其他變量投影重要性指標絕對值皆小于1，說明在本模型中，這4個指標是構成車站客流集散量的最重要影響因素。其中停車場、文物古跡與全日客流集散量成負相關。

表3 全日集散量VIP值

將樣本點的實測全日集散量與模型擬合集散量的結果進行對比，結果如圖1所示。除個別車站外，模型擬合結果與實際值基本吻合。應用擬合模型計算西安地鐵二號線的所有車站的全日客流集散量，并與實際值進行對比，如圖2所示。模型擬合的精度整體良好。由于西安北客站屬于地鐵和高鐵銜接的換乘站，乘降量受對外交通用地和鐵路用地影響較大，本次模型選取車站，不存在此兩類用地，故北客站的模型擬合較差。

圖1 全日集散量擬合結果

圖2 全日集散量預測模型校驗

3.2 早高峰進、出站客流量

早高峰進、出站客流量模型VIP值如表4所示。

表4 早高峰進、出站客流量VIP值

對于早高峰進站客流量，居住用地、行政辦公、商業金融、文化娛樂、公共綠地、市政用地、文物古跡和建筑密度的變量投影重要性指標絕對值均超過1，說明它們是構成早高峰進站客流量的最重要影響因素。早高峰進站客流多以上班、上學、通勤交通為主，行政辦公、文物古跡、文化娛樂、商業金融這些類型用地多為早高峰出行的終點，屬于吸引性質的用地，與進站客流量成負相關。

對于早高峰出站客流量，建筑容積率、建筑密度、商業金融、居住用地的變量投影重要性指標絕對值均超過1，說明這4個指標是構成早高峰出站客流量的最重要影響因素。

將樣本點的實測早高峰進、出站客流量與模型擬合結果進行對比，如圖3、4所示。除個別車站外，模型擬合結果與實測值基本吻合。

圖3 早高峰進站客流量擬合結果

圖4 早高峰出站客流量擬合結果

應用擬合模型計算西安地鐵二號線的所有車站的早高峰進、出站客流量，并與實際值進行對比，如圖5、6所示。模型計算結果的精度整體良好。西安北客站屬于地鐵和高鐵銜接的樞紐站，進、出站客流量受高鐵客流影響，模型計算結果誤差較大。

圖5 早高峰進站客流量預測模型校驗

圖6 早高峰出站客流量預測模型校驗

3.3 晚高峰進、出站客流量

晚高峰進、出站客流量模型VIP值如表5所示。

表5 晚高峰進、出站客流量VIP值

對于晚高峰進站客流量，建筑容積率、建筑密度、商業金融、居住用地的變量投影重要性指標值均超過1，說明這4個指標是構成晚高峰進站客流量的最重要影響因素。

對于晚高峰出站客流量，建筑容積率、建筑密度、公共綠地、居住用地、教育科研、醫療衛生、行政辦公的變量投影重要性指標絕對值均超過1，說明這7個指標是構成晚高峰出站客流量的最重要影響因素。晚高峰出站客流量的影響因素較多，影響力較為分散。晚高峰出站客流多以下班通勤客流為主，公共綠地、居住用地多屬于客流吸引源，與車站晚高峰出站客流量呈正相關；而醫療衛生、行政辦公、文物古跡在晚高峰期間屬于客流發生源，故與晚高峰出站客流量呈負相關。

將樣本點的實測晚高峰進、出站客流量與模型擬合結果進行對比，如圖7、8所示。除個別車站外，模型擬合結果與實測值基本吻合。

圖7 晚高峰進站客流量擬合結果

圖8 晚高峰出站客流量擬合結果

應用擬合模型計算西安地鐵二號線的所有車站的晚高峰進、出站客流量，并與實際值進行對比，如圖9、10所示。模型擬合結果的精度整體良好。

圖9 晚高峰進站客流量預測模型校驗

圖10 晚高峰出站客流量預測模型校驗

4 結論

用地類型和軌道客流之間有很強的相關性，各因素之間又存在較強的共線性。在探討用地類型對軌道車站客流乘降量的影響時，僅依靠多元線性回歸獲得的模型穩健性較差，甚至得到錯誤的參數估計。PLSR法因采用分解和篩選數據信息的方式，提取對系統解釋能力最強的成分，故能較好地克服多重共線性在系統建模中的影響，因而相對于多元線性回歸和主成分分析，模型的參數估計也更加準確。

建模的結果表明：不同用地類型對軌道交通客流量有不同的影響，針對不同類型的客流，預測中必須重點把握其對應的重要指標。在一些特殊用地的車站，因變量未選取其比重較大的用地指標時，擬合精度較低。模型在選取自變量指標方面應進一步完善。在準確把握各類型規劃用地的基礎上，車站客流量可以通過PLSR模型進行測算估計。

隨著城市軌道交通的建設，城市軌道交通的總里程迅速增長，線路之間形成網絡，乘客到達目的地的可達性增加，加之其準時、快捷、方便、舒適的特點，使得城市軌道交通的客運量、客運強度大大增加。因此，能準確地預測短期進站客流變化情況，分析乘客出行特征，合理地對進站客流進行有效疏導，對車站內乘客流線的組織、列車的運營時刻表進行相應的安排，是提高乘客出行效率、舒適度，保證安全、高效地運營城市軌道交通線路的重要舉措。