基于后緣厚度變化的翼型噪聲分析研究

文|任旺，李成良，毛曉娥，周捍瓏，金子博

伴隨著風電機組趨于大型化，風電機組產生的氣動噪聲對附近居民的生活造成了較大的影響。目前，低噪聲設計已經成為風電機組的關鍵技術指標之一。風力發電的噪聲主要有機械噪聲和氣動噪聲。隨著近年來機械噪聲的大幅度降低，氣動噪聲的解決便成了現階段風電機組噪聲研究的方向。風電機組氣動噪聲主要包括入流風輪擾動、塔架擾動、葉尖渦流、葉片后緣分離及邊界層分離等。由于在一定工況下后緣分離噪聲在葉片噪聲中占主導地位，因此，深入研究后緣厚度變化對噪聲影響的機理，對低噪聲葉片設計時翼型的選擇具有重要意義。

本文對原始DU91-W2-250翼型以及變后緣厚度翼型附近的流場進行了LES數值模擬，并在此基礎上采用FW-H積分方法數值求解了原始翼型以及變厚度翼型的遠場噪聲，分析了后緣厚度變化對噪聲影響的機理。計算結果表明，后緣厚度減小能夠更有效地改善翼型尾緣渦脫落的情況，降低翼型氣動噪聲水平。

聲類比混合計算方法和FW-H方法

聲類比混合計算方法的特點在于流場和聲場計算是分離的，聲場計算可根據氣動聲學理論在流場計算的后處理中完成。遠聲場可利用已得到的聲源域的數據，通過積分方法或者別的數值方法求解聲類比方程得到，該方法是基于流場到聲場的單向耦合，即非定常流動產生聲波并改變其傳播，但聲波對流場卻沒有顯著的影響。

應用該方法進行氣動噪聲預測時，在獲得近場流動解的基礎上，將近場流動解作為聲源信號，運用FW-H公式積分求得遠場觀測點的氣動噪聲。Ffowes和Hawkings應用廣義函數法解決了流體中任意運動發聲的問題，得到一個較為普適的方程——FW-H方程：

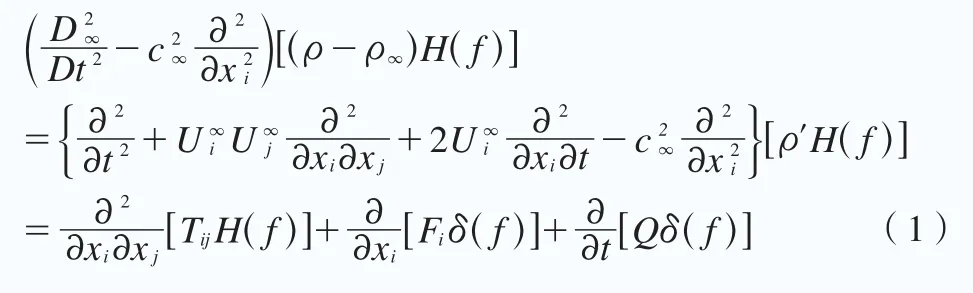
式中，ρ為流體密度；ρ∞為無窮遠處流體密度；為觀察區某一均勻介質的平均速度。Tij為Lighthill張量，其公式為：

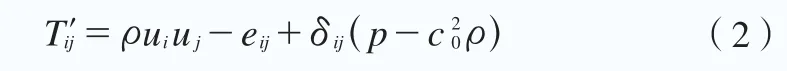
引入流體變量的分解量：

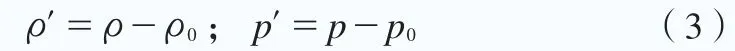
式中，ρ0和p0分別為未受擾動時流體的密度和流場壓強的均值；ρ'和p'分別為流體密度和流場壓強的波動量。

引入Heaviside廣義函數：

式（1）FW-H方程右邊三項表示主要類型的聲輻射源：第一項是流體本身湍流引起的四極子聲源；第二項是施加在物體表面的力引起的偶極子聲源；第三項是進入流體中的非穩定質量流引起的單極子聲源。

DU91-W2-250翼型氣動噪聲數值計算

由于葉片的氣動噪聲主要集中在葉尖部分，這部分的翼型都是薄翼型，根據對業內主要型號葉片翼型的調研，在滿足薄翼型和具有后緣厚度的前提下，選取DU91-W2-250翼型作為研究對象。

一、計算模型與計算網格

在本計算中，使用POINTWISE進行網格劃分，翼型弦長為1.76m，雷諾數為6E6，馬赫數為0.15，計算域為圓形區域，計算域尺寸為翼型弦長的100倍，翼型位于計算域中心，采用結構化網格，網格量為20萬，第一層近壁面網格高度為5e-5m，y+<1。

本文計算采用了三個后緣厚度的翼型，原始翼型是DU91-W2-250，其后緣厚度是12mm，另外兩個翼型在原始翼型的基礎上進行厚度調整。調整方法為：利用Q-bladed在保證PS面不變的基礎上調整SS面尾緣部分，改變后緣厚度，使其厚度分別為0mm和20mm。三種翼型分別稱為Ori-foil、Thin-foil、Thick-foil（下同），幾何模型及網格示意圖如圖1－圖4所示。

圖1 外場計算域示意圖

圖2 Ori-foil近壁面網格分布

圖3 Thin-foil近壁面網格分布

圖4 Thick-foil近壁面網格分布

二、流場計算結果及分析

計算的來流條件為：馬赫數為0.15，攻角為0°。使用FLUENT進行流場計算。

首先，利用K-W sst模型進行穩態計算，通過10000步時間步，獲得穩定的流場。非定常計算采用LES方法，時間步長為t＝5e-5s。根據香農采樣定理可知，該時間步長可以捕捉到的最大頻率為fmax＝1/（2t）＝ 10kHz。總共記錄的聲源數據時間步數為n＝5000步，聲源記錄時間為t＝t.n＝0.25s，因此經過FFT的聲壓級頻譜曲線頻率的分辨率為f＝ 1/t＝ 4Hz。

（一）流場壓力特性

不同后緣厚度翼型流場中，觀察翼型表面，特別是尾緣部分的壓力特性，Cp為翼型表面壓力系數。

由圖5可知，后緣厚度的改變引起了翼型后緣部分的壓力分布變化。在下翼面，后緣厚度改變導致靠近尾緣部分的壓力系數減小，壓力分布也更加均勻，這主要是由于后緣部分的渦脫落情況減輕，導致尾緣部分流場的一致性更好。

（二）流場渦量特性

在不同后緣厚度翼型流場中，觀察翼型附近流場，特別是尾緣部分的渦量分布。

攻角為0°時，各翼型表面壓力系數分布情況如圖6所示。

由圖6可以看到，后緣厚度的改變影響了翼型表面的渦量分布（主要是尾緣渦量）。可以看到當后緣厚度增大時，靠近尾緣的渦核能量增大，但是脫落渦的渦核能量減小；當后緣厚度減小時，后緣脫落渦分布密度下降。

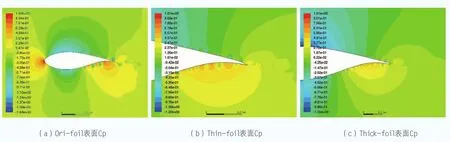
圖5 流場壓力分布

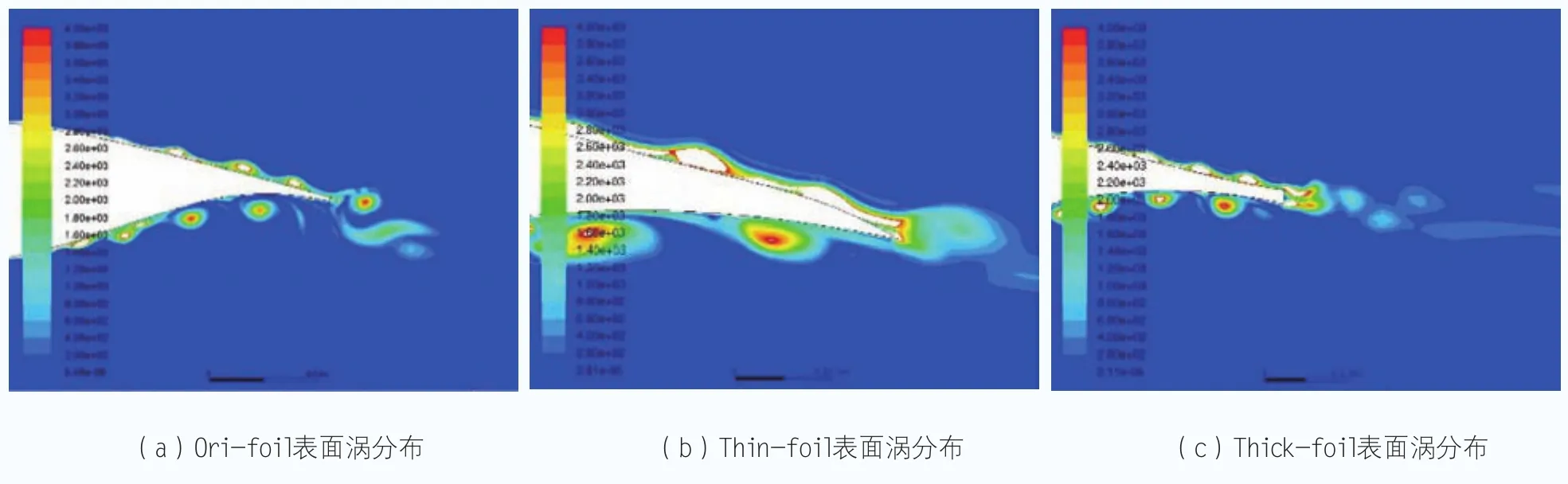
圖6 流場渦量分布

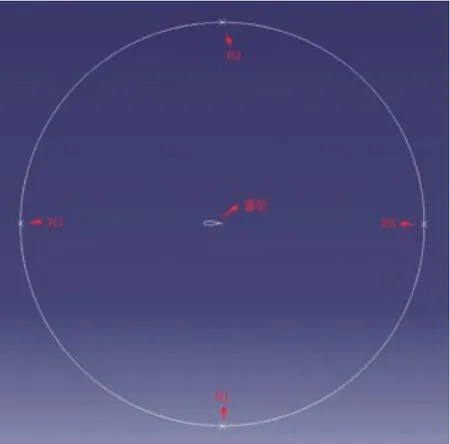
圖7 測量點位置示意圖

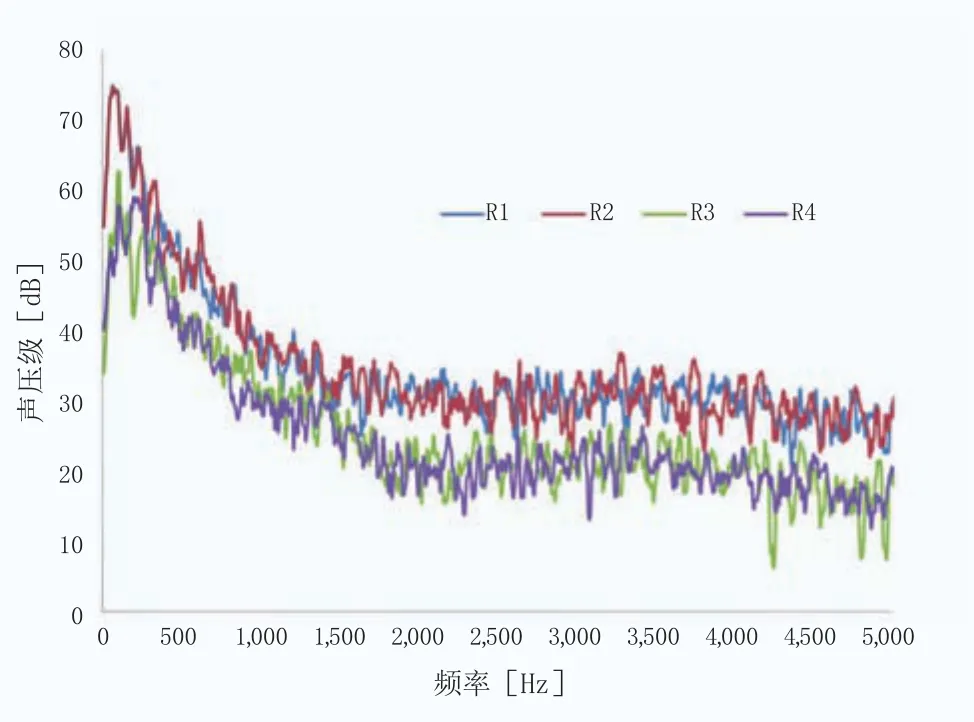
圖8 Ori-foil頻譜特性

表1 各監測點總噪聲聲壓級水平

三、仿真聲場特性分析

（一）原始翼型頻譜特性

馬赫數為0.15，四個測量點分別分布在翼型的四個方位（圖7），測量點坐標分別為R1（0，-17.6，0）、R2（0，17.6，0）、R3（17.6，0，0）及 R4（-17.6，0，0），測量點位處的頻譜特性曲線如圖8所示。

由圖8可知，翼型頻譜特性呈現出低頻特性，噪聲能量峰值出現在低頻部分70～100Hz。翼型噪聲在上下翼面的位置表現得更為明顯，即R1、R2兩個監測點，這和表1中各監測點的總噪聲聲壓級水平也是吻合的。

（二）翼型頻譜特性對比分析

由圖8及表1可知，監測點R1、R2位置處翼型噪聲表征更為明顯，故對不同后緣厚度的翼型在R1、R2觀測點處的頻譜特性與聲壓級水平進行對比分析。

由圖9、10及表2可知，翼型后緣厚度的改變引起噪聲聲壓級水平的下降。在噪聲頻譜圖里可以看到后緣厚度改變后，噪聲峰值頻率明顯增大，從70～100Hz變為350～400Hz。在低頻部分，后緣厚度的變化會引起噪聲的增加，但峰值沒有超過原始翼型；當厚度減小時，低頻部分噪聲的增幅更明顯；在高頻部分，后緣厚度的改變明顯降低了噪聲幅值，這主要是由翼型表面，特別是尾緣部分的表面脈動壓力頻率的下降所致。結合翼型流場渦量圖可以發現，噪聲水平和尾緣實際流動關系密切，尾緣渦量的脫落密度、渦核能量密度直接影響了聲壓級水平。

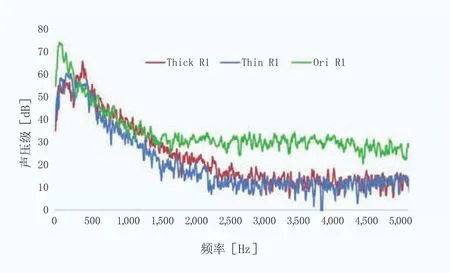
圖9 R1處各翼型噪聲頻譜特性

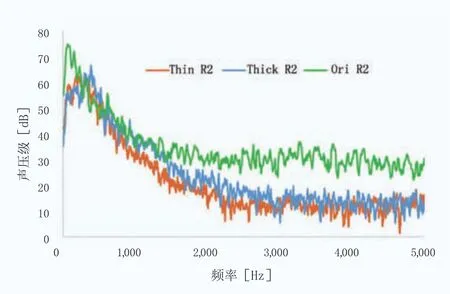
圖10 R2處各翼型噪聲頻譜特性

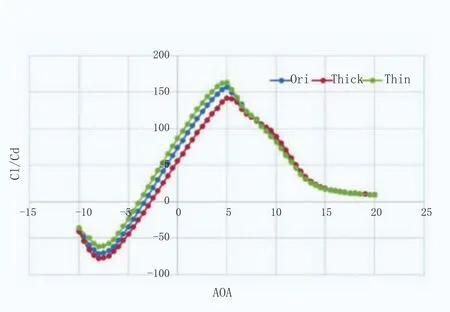
圖11 升阻力曲線

表2 R1/R2處各翼型噪聲聲壓級水平

在噪聲聲壓級水平方面，在監測點R1處，Thick翼型相較于原始翼型，噪聲下降8dB，Thin翼型下降約10dB；在監測點R2處，Thick翼型相較于原始翼型，噪聲下降7.5dB，Thin翼型下降約9.3dB。

翼型氣動性能變化

由于葉片設計時，不僅要考慮翼型噪聲表現，還要特別注意翼型的氣動性能表現。故通過Rfoil對三種不同厚度翼型的氣動性能進行計算，并對升阻比的計算結果進行對比分析。

由圖11可以明顯發現：翼型尾緣厚度減小后，升阻力在失速前的表現明顯變好，Cl/Cdmax相對于原始翼型從153增大到163，失速后的表現和原始翼型基本一致；后緣厚度增大后，翼型失速前性能下降明顯，Cl/Cdmax相對于原始翼型，從153降低為143，在8.5°～11.5°范圍內失速性能較原始翼型稍微有所提升。

總結

通過對DU91-W2-250翼型進行流場及聲場的仿真計算發現，翼型后緣厚度變化后，噪聲峰值頻率明顯增大，從70～100Hz變為350～400Hz。在低頻部分，噪聲有所增加，但峰值沒有超過原始翼型，厚度減小后，低頻部分噪聲的增幅更明顯；在高頻部分，后緣厚度的改變明顯降低了噪聲幅值。在降低噪聲聲壓級水平上，后緣厚度減小明顯大于后緣厚度增大。此外，翼型后緣厚度的變化明顯影響了翼型的氣動性能，翼型尾緣厚度減小后，升阻力在失速前的表現明顯變好；后緣厚度增大后，翼型失速前性能下降明顯。

綜上所述，在設計翼型時，后緣厚度越薄越好。當然在具體設計時還應該結合結構與工藝的可實現性。