基于MLP法的磁浮列車非線性系統的穩定性分析

楊志安，崔佳磊

(1.唐山學院 唐山市結構與振動工程重點實驗室，河北 唐山 063000；.華北理工大學 機械工程學院，河北 唐山 063210)

0 引言

磁浮列車通過電磁力將列車控制在一定高度，實現列車與軌道之間無機械接觸，然后通過直線電機驅動列車。它具有速度快、爬坡能力強、能耗低、運行噪音低、安全、舒適、污染小等優點[1]。磁浮列車的懸浮能力直接決定了車輛的承載能力，而懸浮能力的大小取決于懸浮控制系統。懸浮控制的基本要求是保證列車在各種內外干擾力作用下能夠穩定的運行。

研究磁浮列車穩定性問題，首先要建立正確的動力學模型，磁浮列車屬于機電磁耦合系統，拉格朗日-麥克斯韋方程是建立機電系統模型的一種核心方法。經典的拉格朗日-麥克斯韋方程是基于線性的電場能We和線性的磁場能Wm，以電荷、電流作為廣義坐標得到的[2]。2007年文獻[3]中推廣了拉格朗日-麥克斯韋方程的應用范圍，使之適合于電磁非線性情況。2012年，文獻[4]將機電系統的狀態變量與力學系統的廣義坐標相聯系，得到了經典形式的拉格朗日-麥克斯韋方程，使機電分析動力學的核心內容更加完善。

MLP法，是在攝動法小參數的基礎上引入非小參數，小參數的來源是將非線性有關的參數利用冪級數進行展開，并且展開的要求是其后的每一項都要小于前一項。非小參數是由小參數變換而來。將非線性微分方程轉化為線性隨機微分方程組，最后用此方法就可以求解了。與等效線性化方法一樣，MLP法只能得到響應的時域信息，而不能得到響應的頻域信息，因為非線性系統的頻率沒有可保存性，所以頻域信息是不穩定的， 理論上難以獲得[5]。

Wu等人提出了一種基于T-S模糊數學模型的非線性電磁懸浮系統模糊控制方法，仿真結果表明，該方法在處理有界擾動時有效，但同時卻增加了控制器設計的復雜度[6]。施曉紅等人從磁浮列車-軌道耦合的非線性特性的角度研究了靜懸架條件下磁浮列車-軌道耦合系統的控制參數、軌道參數與振動特性之間的相關關系[7]。楊霞等人研究了單磁懸浮系統，建立了磁懸浮系統在平衡點的狀態方程，并采用極點配置法使系統滿足穩定性條件，在此基礎上，對磁懸浮系統進行了數值模擬分析，最后得出結論，狀態空間控制方法能有效地穩定磁懸浮系統[8]。

在眾多的磁浮系統研究中，學者們對轉向架、電磁力、車-軌耦合振動、車輛運行穩定性以及懸架控制器的設計等問題進行了研究，主要研究方向集中在磁浮列車的線性系統上。本文主要根據拉格朗日-麥克斯韋方程建立關于磁浮系統的非線性動力學模型，利用MLP法來研究主共振的幅頻響應方程。

1 磁浮列車懸浮系統動力學模型的建立

常導型磁浮列車懸浮系統簡圖如圖1所示，列車的車廂下方裝有電磁鐵，電磁鐵吸向“T”型鋼軌，當電磁鐵繞組中的電流及在電磁鐵與鋼軌間的氣隙均為標稱值的情況下，懸浮拉力和車廂的重力平衡。

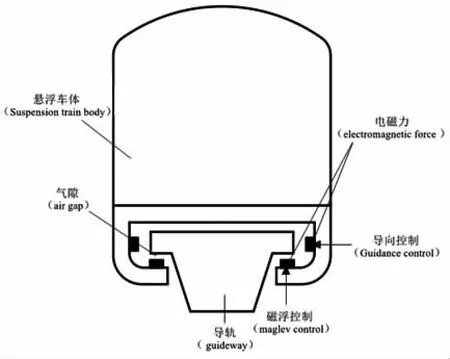
圖1 磁浮列車懸浮系統簡圖

當磁浮列車車廂沿鉛垂軸方向做直線平動，且在通電之后處于平衡狀態時，電磁鐵與鋼軌間的氣隙為標稱值，車廂質心與原點O重合。以Δy表示車廂的小位移，以i表示電磁鐵繞組中的電流。所研究的磁懸浮機電系統的廣義坐標為Δy，i。磁浮系統的物理模型見圖2。

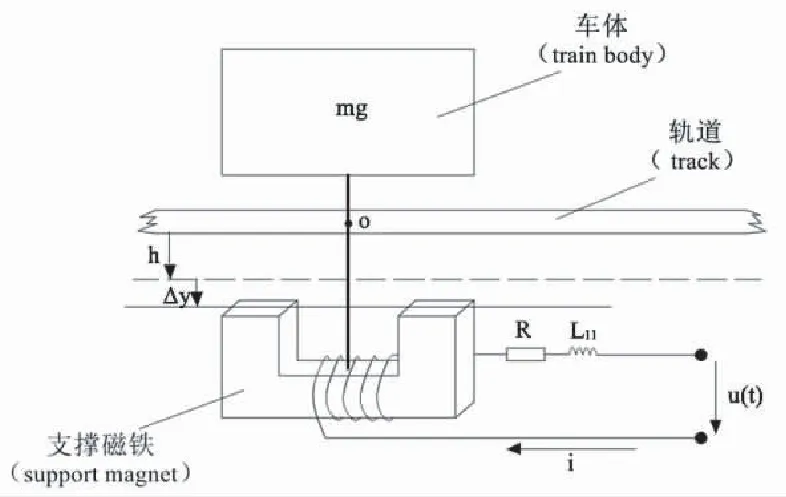
圖2 磁浮系統的物理模型

將懸浮車廂看作一個剛體，利用剛體平動的動能公式得到車廂的動能公式：

(1)

懸浮車廂的重力勢能為：

V=mgΔy。

(2)

磁場能量計算公式為：

(3)

式中V為磁場包圍的體積，B為磁感應強度。

假定電磁鐵與鋼軌間的氣隙h-Δy和U型電磁鐵的截面積s相比很小。這時在電磁鐵與鋼軌之間的氣隙中磁場可以認為是均勻的，并且可以忽略邊界效應，在鋼軌、磁鐵、氣隙之間以外的漏磁場可以忽略。假定在鋼軌與磁鐵中的磁導率μ非常之大，因此沿磁鐵與鋼軌的體積內的磁能相比于磁鐵與鋼軌間隙內的磁能很小，因此可以忽略。根據以上的假設對式(3)進行計算時，在兩個氣隙內的磁感應強度B可以看作常量，于是由式(3)計算得到：

(4)

式中μ0為氣隙磁導系數。

通過電磁鐵的磁通為：

φ=BSN，

(5)

上式中N為繞組的匝數。

根據磁通和電流成正比的關系可得：

φ=L11i，

(6)

上式中，L11為線圈的自感系數，i0為標稱電流。

由式(5)及式(6)可得到磁感應強度為：

(7)

將式(7)代入磁能公式(4)中，得到

(8)

同時磁能公式還可以表示為：

(9)

同樣由式(8)及式(9)可以得到自感系數關于廣義坐標的表達式：

(10)

再將式(10)代入式(9)得到磁能關于廣義坐標以及電流的表達式：

(11)

根據能量守恒定律，利用拉格朗日-麥克斯韋方程來建立磁浮系統的動力學模型，將式(1)(2)(11)代入Lagrange方程：

L=T+Wm-V=

(12)

耗散函數的表達式為：

(13)

上式中，b為車廂運動的粘性阻力系數，R為線圈的電阻。

假定不存在機械的非保守廣義力，用u(t)表示作用于電磁鐵中的電壓。為了保證列車車廂的穩定性，這個電壓要依賴測量電磁鐵與鋼軌間氣隙大小的指示傳感器，當氣隙增大時則電路中的電流也必須增大，以便增加磁鐵與鋼軌間的電磁拉力，使車廂回到平衡狀態；相反，當氣隙減小時則需要減小電流的輸入，以便減小電磁拉力，使車廂保持平衡狀態。

磁浮列車懸浮系統的拉格朗日-麥克斯韋方程的形式為[2]：

(14)

將式(12)及式(13)代入式(14)中，并經過一定的微分運算得到磁浮列車車廂的運動微分方程：

(15)

式(15)中，(b)式的第一項是非線性項，為鋼軌間氣隙的倒數與電流的變化率的乘積，(b)式的第二項同樣是非線性項，(a)式的第三項也是非線性項，所以該方程組是一個三階的非線性方程。因為其計算復雜，且不好處理，所以現階段幾乎沒有學者對其非線性項進行詳細的研究。

2 主共振分析

假設式(15)中u(t)=u0cosωt，也就是說將電壓看作是激勵電壓，u0是常數，當車廂處于平衡位置時

(16)

將式(16)代入式(15)可以得到u0和i0的值：

u0=Ri0；i02=2mg/L0，

(17)

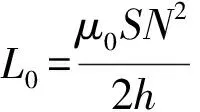
當車廂位移很小時，即Δy?h時，磁鐵中的電流和本生的標稱值i0相近，此時引入小參數α，此時式(15)中的電流i為：

i=i0+αx。

(18)

利用上述理論將式(15)化為：

(19)

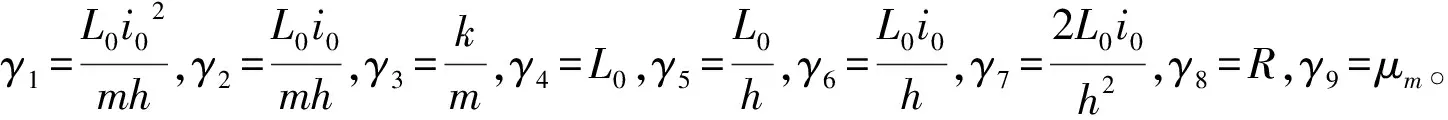
將式(19)中的第2式子代入第1式得到：

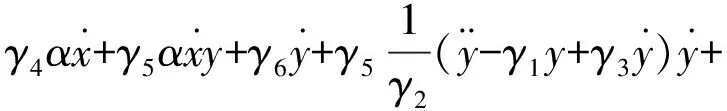
(20)

繼續完善式(19)，得：

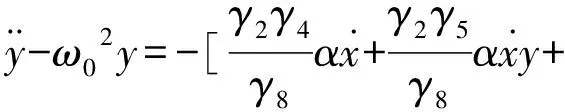
(21)

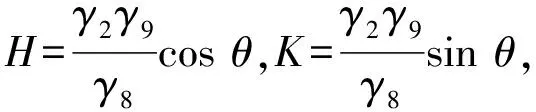
(22)

令ω2=ω02+εω1+ε2ω2+…。

(23)

引入參數變換，此時小參數α用非小參數ε近似表示：

(24)

反解出非小參數ε：

(25)

將式(25)代入式(23)可得：

(26)

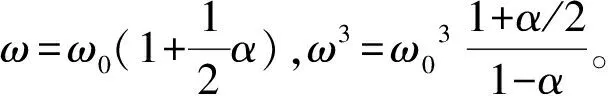
(27)

對y采用攝動法[9]展開：

y=y0+αy1+α2y2+…。

(28)

利用上述論述，將式(22)化為：

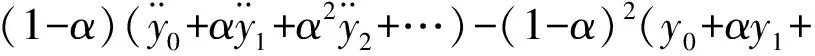
(29)

比較方程兩邊α的冪次得：

(30)

(31)

(32)

式(30)的基解，即式(22)的零次近似解：

y0=Ae-τ+Beτ。

(33)

將基解式(33)代入式(31)，得到動力學模型的一次可求永年項的表達式。同理，利用式(32)可得到方程(22)的二次可求永年項表達式。再根據永年項的定義，即隨時間增加趨于無窮的項[10]，也就是在所得到的二次可求永年項表達式中含有eτ，e2τ，e3τ，也就是說系統發生振幅無限的共振。若要使磁浮系統做周期平穩運動，需要消除永年項。為此令所得式中的eτ，e2τ，e3τ項的系數為零。

(34)

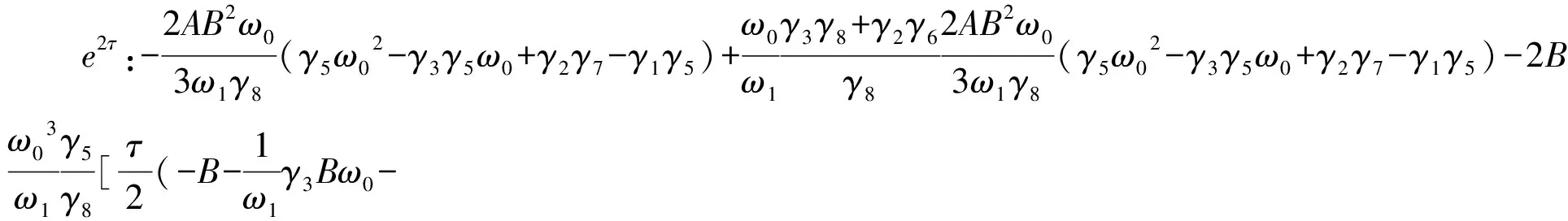
(35)

(36)

3 數值模擬

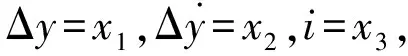
(37)

在利用Matlab進行計算之前，需要為式(37)中的各個參數賦值，且確定式(37)的初始條件。

各參數的取值分別為：R=1 Ω，m=61 000 kg，μ0=4π×10-7H/m，S=0.021 m2，i0=30 A，N=356，k=8.46×104N·s/m，h=0.01 m，ω=100 π rad/s，u=220 V。

設式(37)非線性微分方程組的初始條件分別為：

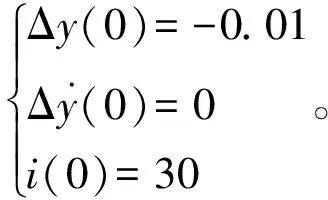
(38)

通過四階龍格庫塔法計算并繪制出50 s內磁浮列車懸浮系統在空載、滿載、過載不同載荷下的時間響應曲線以及相圖，見圖3-8。

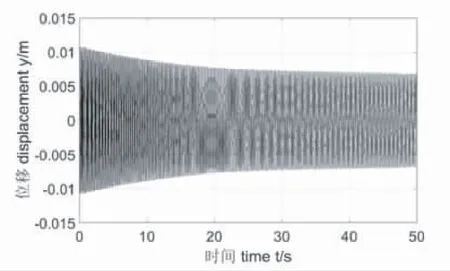
圖3 m=60 000 kg時間響應曲線

圖4 m=69 000 kg時間響應曲線

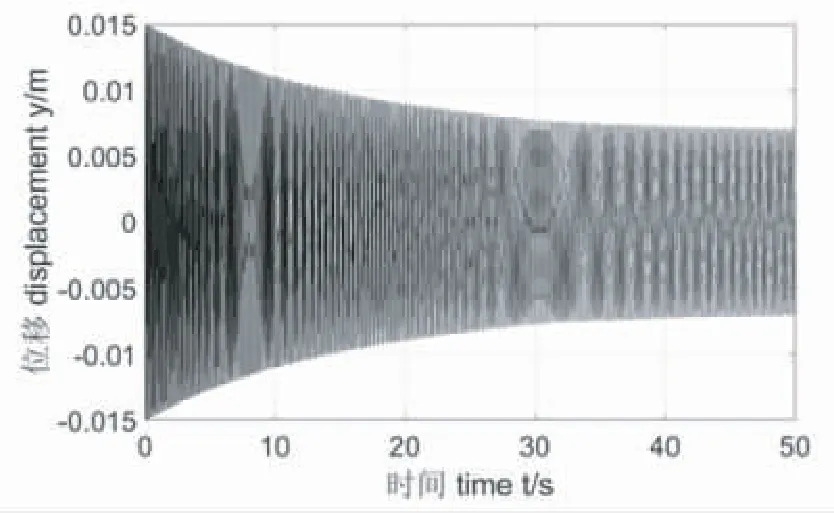
圖5 m=70 800 kg時間響應曲線

圖6 m=60 000 kg相圖

圖7 m=69 000 kg相圖

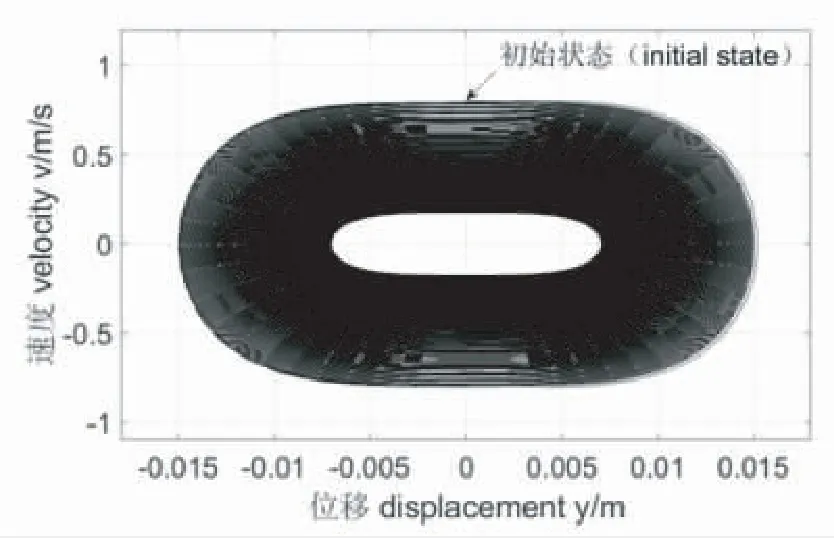
圖8 m=70 800 kg相圖

從圖3到圖5可以看出，隨著磁浮列車質量的增加，列車初始位移會增大，但隨著時間的推移，列車都會趨于穩定。從圖6到圖8的相圖可以看出，隨著磁浮列車質量的增加，列車初始位移會增大，列車的垂向振動速度在減小，這表示列車會趨于穩定。

4 結論

(1)選取間隙和電流為廣義坐標，利用拉格朗日-麥克斯韋方程建立磁浮列車懸浮系統的運動模型。該模型屬于三階非線性微分方程。

(2)改變MLP法的基解形式，是考慮到微分方程的形式同傳統的振動微分方程不同，其基解的表達式為指數形式，不同于正剛度的三角函數形式，最終得到三個不同指數冪的表達式，這也不同于正剛度的三角函數形式，三角函數形式只能有兩個表達式，指數形式涉及到的不定參數過多而無法進行求解。

(3)在空載、滿載、過載情況下，模擬時間為50 s時的懸浮系統振動時間響應曲線，由相圖可知，列車質量增加，列車初始位移會增大，但列車起動后經過一定的時間，系統振動趨于穩定。