一種齊當別思想下的量子決策模型：對囚徒困境中的分離效應的解釋*

辛瀟洋 李 瑛 畢研玲 晏碧華

?

一種齊當別思想下的量子決策模型：對囚徒困境中的分離效應的解釋

辛瀟洋 李 瑛 畢研玲 晏碧華

(陜西師范大學心理學院暨陜西省行為與認知神經科學重點實驗室, 西安 710062)

量子決策模型是近10年來提出的一種新型決策模型, 用以解釋那些違背經典決策模型的現象。雖然當前的量子決策模型能夠解釋囚徒困境中的分離效應, 但其中卻存在一些困難, 即會產生反常的概率關系以及無法精確擬合分離效應量較大的實驗結果。本研究在分析當前量子決策模型困難的基礎上, 結合齊當別思想對模型進行改進和優化。結果表明, 研究所構建的量子決策模型克服了當前模型中的困難, 并且能夠預測囚徒困境博弈中由他人收益差距改變而引起的分離效應變化趨勢。本研究還是一次啟發式決策模型與計算式決策模型相結合的探索。

量子; 決策; 齊當別; 分離效應; 囚徒困境

1 引言

早期的決策研究大都遵循個體完全理性的理論假設, 認為人們的決策是追求自我利益的最大化。在這種早期“經典”理論的影響之下, Savage (1954)提出了確定事件(sure-thing principle)原則, 所謂確定事件原則是指如果決策者知道事件E會發生, 他會采取行動A; 如果決策者知道事件E不會發生, 他仍會采取行動A; 以此觀之, 決策者在不知道事件E是否會發生的情況下, 也會采取行動A。然而, 大量研究表明, 決策者并非總是遵循這一原則, 即當決策者不知道事件E是否會發生的情況下, 他會拒絕行動A, 這一現象被稱為分離效應(Tversky & Shafir, 1992; 汪祚軍, 李紓, 2008)。

一系列的研究已經證實, 在一次性二人囚徒困境博弈中, 決策者的行為往往也會違背確定事件原則, 出現分離效應(Busemeyer, Matthew, & Wang, 2006; Croson, 1999; Li & Taplin, 2002; Tversky & Shafir, 1992)。在這一博弈中, 只有合作和背叛兩種策略可供博弈雙方選擇。無論對方選擇合作還是背叛, 當自己選擇背叛時, 收益是最大的(標準囚徒困境博弈中的收益矩陣如表1所示, 其中π>π>π>π) (Denolf, Martínez, Josephy, & Duran, 2017; Smith, 1982), 因此選擇背叛是決策雙方的優勢策略。根據確定事件原則, 在對方策略不明的情況下, 決策者做出背叛的可能性應該介于兩種確定的狀態(對方背叛、對方合作)下決策者背叛的可能性之間。但實驗結果表明, 此時決策者背叛的可能性小于兩種確定狀態下決策者背叛的可能性, 即出現了分離效應。例如, 在Shafir和Tversky (1992)的研究中,在兩種確定情況下(已知對手背叛/合作), 決策者選擇背叛的概率分別為97%和84%, 而在對手決策未知這一情況下, 決策者選擇背叛的概率卻只有63%。

表1 標準囚徒困境博弈中收益矩陣

近10年來, 一些學者基于量子理論研究思想與方法探索出了量子決策模型, 為解釋諸如分離效應這樣違背傳統決策理論的現象提供了新思路。量子決策模型能夠給出獨立于模型的參數和實證數據的預測, 且針對不同研究問題所構建模型的表述形式也不盡相同(Blutner, Pothos, & Bruza, 2013; Bruza, Wang, & Busemeyer, 2015; Busemeyer & Wang, 2015; Busemeyer, Wang, Khrennikov, & Basieva, 2014; 辛瀟洋, 徐晨虹, 陳宏玉, 李瑛, 2018)。其中, 針對囚徒困境中出現的分離效應, Pothos和Busemeyer借鑒認知失調理論構建了可以解釋囚徒困境中分離效應的四維動態量子決策模型(Pothos & Busemeyer, 2009; Busemeyer & Bruza, 2012)。但是, 當前量子決策模型在解釋囚徒困境時, 仍存在一些困難之處。接下來, 本文將首先指出并分析這些困難, 并在此基礎上, 提出解決這些困難的方法。

2 當前量子決策模型的困難

由Jerome R. Busemeyer教授等人提出的, 用以解釋囚徒困境博弈中的分離效應的四維量子決策模型是一種較為成熟的動態量子決策模型, 這種模型及其變式可用來解釋兩階段賭博任務中的分離效應以及分類?決策中的干涉效應等違背傳統決策模型的現象(Busemeyer, Wang, & Lambert-Mogiliansky, 2009; Pothos & Busemeyer, 2009; Busemeyer & Bruza, 2012; Busemeyer, Wang, & Pothos, 2015; Wang & Busemeyer, 2016)。然而, 這種模型在對囚徒困境中分離效應進行分析解釋的過程中, 存在著一些困難, 接下來, 本文將指出這些困難, 并分析產生這些困難的原因。

2.1 四維標準量子決策模型

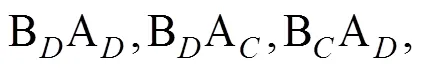
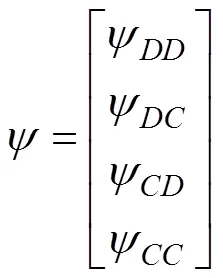
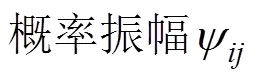
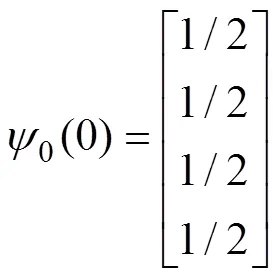
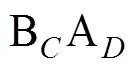
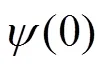
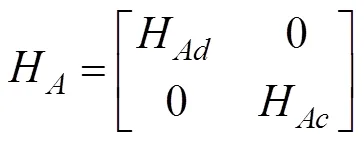
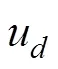
2.2 Pothos和Busemeyer (2009)對四維標準量子決策模型的改進

Pothos和Busemeyer (2009)認為, 決策者在決策過程中會產生認知失調, Wang和Busemeyer (2016)后來將其稱為信念與行為的糾纏(belief-action entanglement), Shafir和Tversky (1992)則把這種個人的偏見表述為“一廂情愿”(wishful thinking), 即當決策者認為對手的策略為合作/背叛時, 他傾向于采取同樣的行動(Festinger, 1957), 這種信念與行動間的關系可由式(4)所示的矩陣表示：

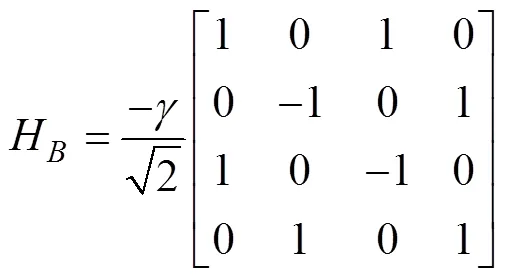
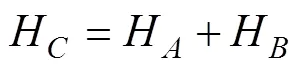
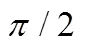
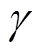
進一步的分析可以發現, 這一區域正對應于圖1(a)中存在明顯分離效應的區域(冷色區域), 也就是說, 圖1(a)中存在分離效應的冷色區域大部分是存在著(背叛│對手合作) >(背叛│對手背叛)這一奇怪關系的“無效”區域。將圖1(a)中這些“無效”區域剔除后的有效區域如圖1(c)所示(彩色部分為有效區域), 此時, 便出現了第二個困難——雖然這一部分能夠解釋的最大分離效應量的絕對值為0.25左右, 但這些極大值區域較少, 對于分離效應量較大的研究結果(如Shafir和Tversky (1992)的研究)依舊難以精確擬合(擬合結果見表2)。

若我們繼續探究的話, 便會發現這一模型的第三個困難, 即無法解釋決策者自身收益之差的效用函數與分離效應量之間的關系。已有的研究已經證實, 當決策者的收益之差增大時, 會導致分離效應的減少(Li & Taplin, 2002; 李紓, 2016)。而從圖1(c)中可以看出, 當增大時, 分離效應量的絕對值反而呈現增加的趨勢。

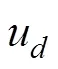
3 一種齊當別思想下的量子決策模型

3.1 齊當別模型對囚徒困境中分離效應的解釋

齊當別模型認為, 左右人類風險決策行為的機制不是最大限度地追求某種形式的期望值, 而是某種形式上辨察選擇對象之間是否存在“優勢性”關系, 并借助最好可能結果和最壞可能結果對問題進行表征。人們必須在一個或幾個維度上將差別較小的可能結果人為地“齊同”掉, 而在差別較大的維度上選擇出具有優勢的選項(Li & Taplin, 2002; 畢研玲, 李紓, 2007; 李紓, 2005; 李紓等, 2009)。因此, 該模型認為, 在一次性標準囚徒困境實驗中, 決策者在不同條件下決策所基于的“維度”是不同的。在兩種確定條件下, 由于在“自己收益維度”上, 背叛明顯優于合作, 因此決策者傾向于將“他人收益維度”上的差異“齊同”掉, 從而在“自己收益維度”上做決策, 選擇對自己有利的行為(背叛); 而在不確定條件下, 由于在“自己收益維度”上, 背叛策略不再明顯地優于合作策略, 而在“他人收益維度”上, 合作策略明顯優于背叛策略, 這樣, 決策者抑或傾向于將“自己收益維度”上的差異“齊同”掉, 而在“他人收益維度”上做決策, 選擇對他人有利的行為(合作) (Li & Taplin, 2002; 李紓, 2016; 汪祚軍, 李紓, 2008)。

表2 不同研究中決策者選擇背叛的概率以及不同量子決策模型的擬合結果

注：括號內為先前的量子模型擬合結果/本研究提出的量子模型的擬合結果

據此可知, 當決策者處于兩種對手策略確定的情況時, 他是基于自己的收益做決策的, 此時量子決策模型中的哈密頓矩陣可根據決策者自身維度上的效用函數進行定義。當決策者處于不確定的決策條件時(對手策略未知), 若決策者只處于“他人收益維度”上, 那么選擇合作便是這一維度上的占優選項, 此時決策者選擇合作的概率應大于選擇背叛的概率, 而這與實際研究結果卻不相符。以此觀之, 此時決策者應該既考慮自己的收益, 又兼顧他人的收益, 因此, 在對手策略未知的情況下, 哈密頓矩陣需要根據決策者以及他人的效用函數進行定義。接下來, 本文將基于以上分析對量子決策模型進行修正與重構。

3.2 齊當別思想下量子決策模型的重構

3.2.1 確定條件下哈密頓矩陣的修正

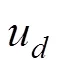
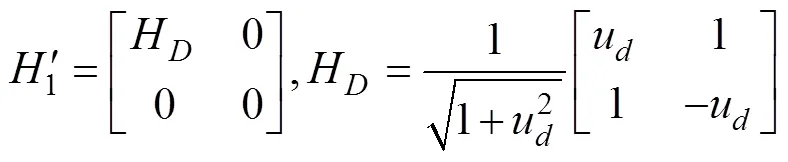
接下來, 我們便需要解決2.1中效用函數過度簡化的問題, 即如何定義一個能夠有效反映決策者收益之差的效用函數。我們選擇使用預期理論中的價值函數, 并對其做適當的歸一處理, 使其取值在?1與1之間, 以滿足量子決策模型對于效用函數取值范圍的要求：

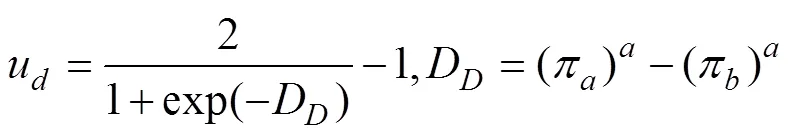
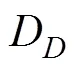
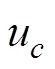
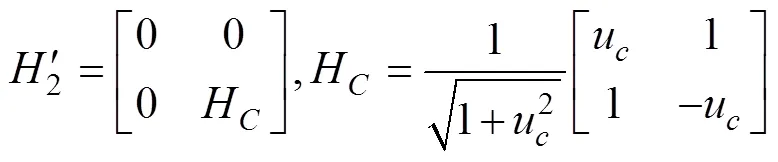
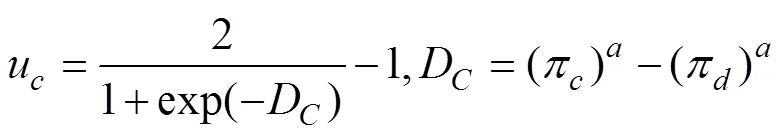
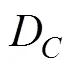
3.2.2 不確定條件下哈密頓矩陣的修正

當對手策略未知時, 決策者會將“他人收益維度”列入自己的決策標準之內。此時, 決策者決策時除了會參考自己的收益維度, 也會考慮他人的收益維度。此時的哈密頓矩陣便可以通過兩個分別代表自身收益和他人收益的哈密頓矩陣疊加而成。

其中, 代表決策者自身收益的哈密頓矩陣可表示為：

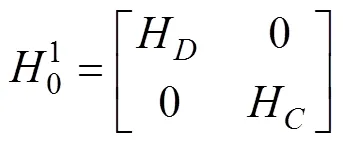
而代表他人收益的哈密頓矩陣可表示為：

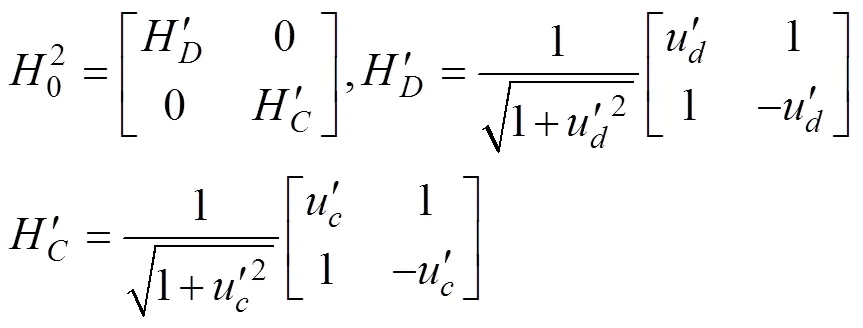
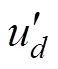
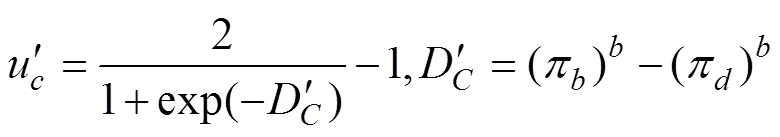
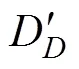
3.3 齊當別思想下的量子決策模型對囚徒困境中分離效應的解釋

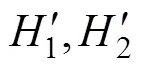
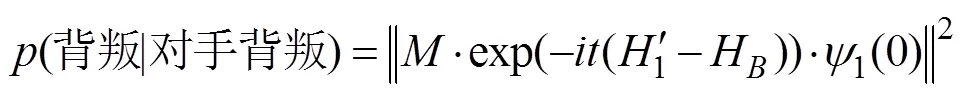
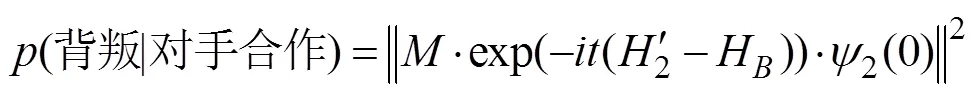
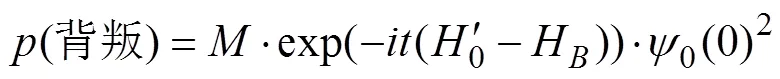
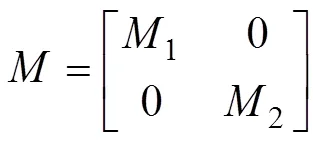
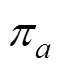
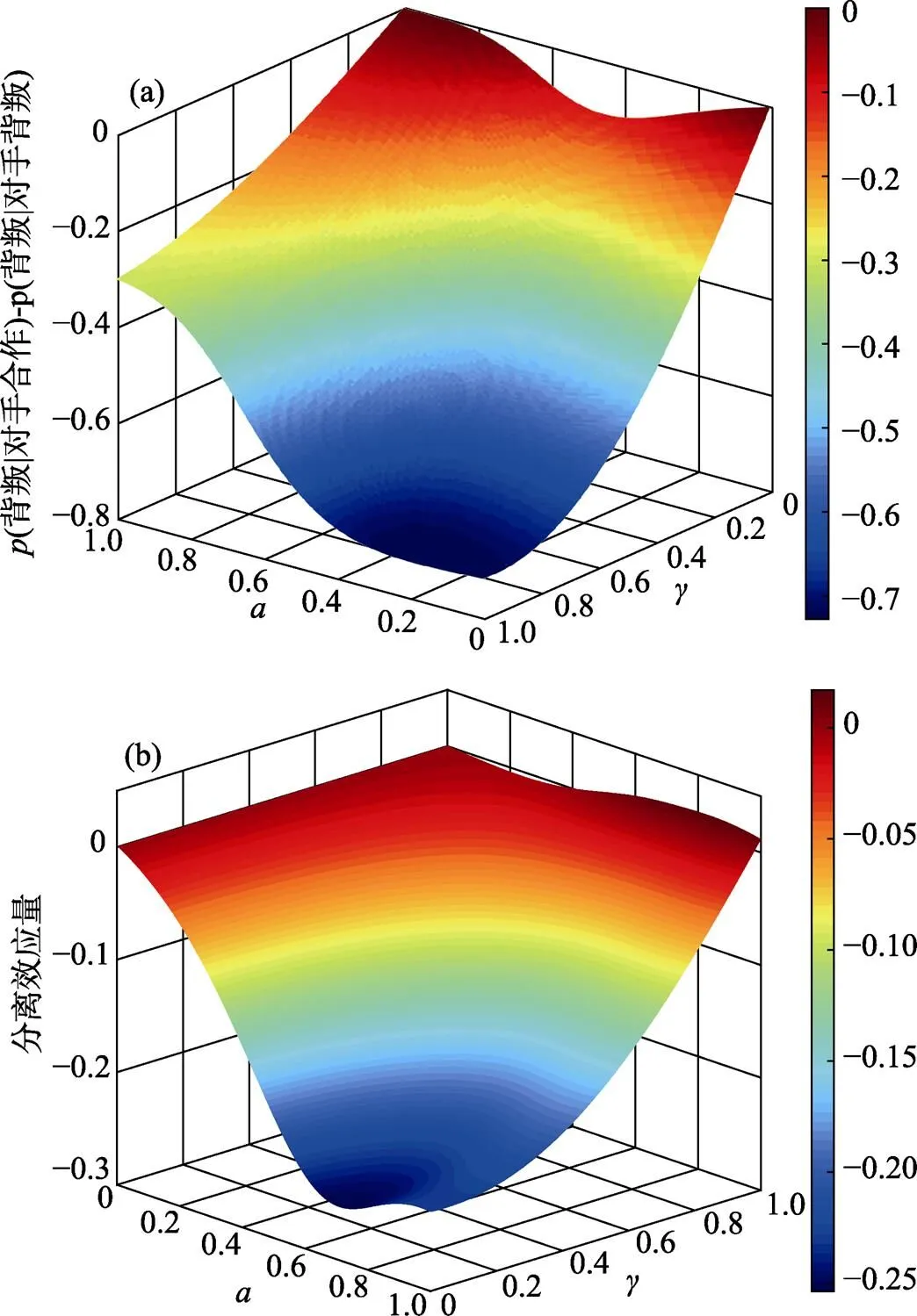
圖2 本研究所提出的量子決策模型中(背叛│對手合作)?(背叛│對手背叛)以及分離效應量與和之間關系的3D著色表面圖(其中模型參數=/4,=3/8)

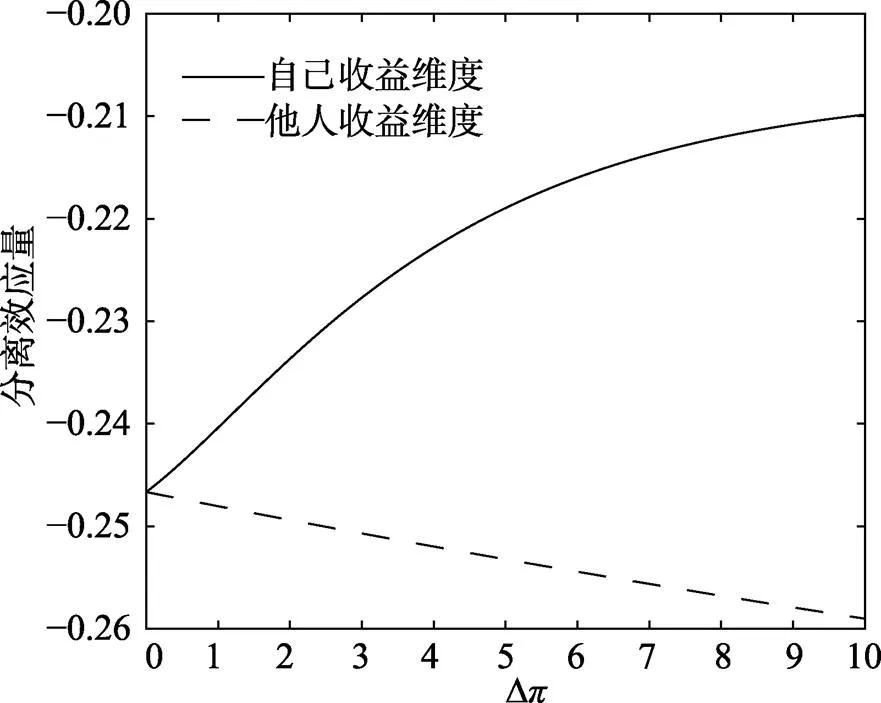
圖3 本研究所提出的量子決策模型中收益增加量Dp與分離效應量之間的關系(模型其余參數為擬合Shafir和Tversky (1992)研究所得參數)

4 討論

4.1 啟發式與計算式的融合

自從Herbert Simon提出“有限理性”的概念以來, 在此基礎上形成的啟發式(Heuristic)決策模型已經在決策領域取得了許多重要的成就(Baron, 2007; Gigerenzer & Todd, 1999; Tversky & Kahneman, 1974)。大多數啟發式決策模型, 例如齊當別模型, 以決策模型的三因素分類體系來看, 屬于非補償性和確定性的決策模型(Stevenson, Busemeyer, & Naylor, 1990)。由于存在非補償性, 這類模型會對一些信息進行簡化或剔除, 進而簡化分析過程; 但由于該模型的確定性(Kubovy, Rapoport, & Tversky, 1971; 李紓, 2016), 使其無法精確描述決策者在不同條件下做出決定的概率。

量子決策模型, 屬于計算式(Computational)或數學(Mathematical)決策模型, 從決策模型的分類體系標準來看, 屬于具有隨機性的決策模型。因為其具有隨機性, 可以通過概率函數的形式表征決策結果, 所以這類模型可以定量描述分離效應(Busemeyer & Townsend, 1993; Payne & Bettman, 2004)。但是, 先前的量子決策模型, 過度簡化了模型的構建過程, 并缺乏對實際決策過程中決策者策略的深入思考。因此, 在解釋分離效應時存在困難。

本研究所提出的量子決策模型, 立足于四維量子決策模型, 借鑒了齊當別思想對模型進行了重構。可以稱之為一種計算式與啟發式相融合的決策模型。而這種齊當別思想下的量子決策模型, 解決了先前量子決策模型中所存在的困難, 同時也為今后決策模型的構建添加了新的可能性。

4.2 囚徒困境中決策者信念與行為的糾纏

本研究所提出的量子決策模型中, 依舊保留了原量子模型中表示信念與行動糾纏的哈密頓矩陣H。那么, 是否可以忽略這一糾纏效應, 進而完全按照齊當別思想來構建量子決策模型呢？本研究的結果表明, 當分離效應量較小時(如Li & Taplan (2002)的研究結果), 模型的最佳擬合參數中=0, 說明此時H是可以去除的; 但當分離效應量較大時, 若去除H, 則會使擬合誤差大幅提升, 如對Shafir和Tversky (1992)的實驗結果進行擬合時, 絕對誤差便會從原先的0.04上升至0.09, 增大了兩倍, 可見此時去除H是不合適的。綜上所述, 信念與行為的糾纏對于解釋分離效應量較大的研究是不可或缺的。

5 結論與展望

本文提出了一種結合齊當別思想的量子決策模型, 研究表明這一模型解決了先前量子決策模型中存在的困難。當然, 正如量子決策模型的奠基者Jerome R. Busemeyer教授所指出的, 類似量子決策模型這樣的數學決策模型, 就像剛剛進入決策之城的小孩子一樣(Busemeyer & Johnson, 2008), 需要不斷地成長才能獲得屬于自己的一席之地。因此, 作為這些“小孩子”中的一員, 本研究所提出的這種量子決策模型, 也有值得進一步探討與發展之處, 主要總結為以下幾點：

(1) 模型的擴展應用。本文提出的這種量子模型, 未來可以嘗試解釋諸如兩階段賭博任務中的分離效應, 以及分類?決策(Categorization-decision)實驗中的干涉效應(Busemeyer et al., 2009; Townsend, Silva, Spencer-Smith, & Wenger, 2000; Wang & Busemeyer, 2016)等違背經典決策模型的問題。

(2) 模型的動態化探究。在量子決策模型中, 由于薛定諤方程以及其解中存在時間參數, 因此量子模型又是一種動態的(Dynamical)模型(Busemeyer, Wang, & Townsend, 2006)。但是, 目前大多數相關研究中, 為了簡化問題探討, 往往將時間設為固定值, 而在實際問題中, 決策時間的不同會對決策者的最終決策產生影響, 而對于量子決策模型來說也是如此, 因此, 探究一種具有“動態化”的量子決策模型也具有重要的理論和現實意義。

(3) 更加“真實”的量子決策模型。包括本研究在內的大多數動態量子決策模型, 都是“理想的”模型。例如, 模型中決策者的信念行為狀態(包括基態以及疊加態), 是一種“純凈的”、“理想的”量子態(純態), 這就意味著決策者(被試)間的差異可以忽略, 模型可以通過平均行為傾向來描述被試群體行為特點; 模型中的測量是“完美的”, 即在測量時(或要求被試報告結果時)所測得的結果能夠完全表示決策者所處的信念行為狀態(Yearsley, 2017)。但是在現實中, 由于受到各種條件的影響(噪音), 決策過程往往不會如此理想化。在未來的研究中, 通過在模型中構建適當的噪音, 不僅可增強模型的真實性, 而且可以據此來判別在一定的情況下是否真的存在分離效應抑或僅僅是實驗中存在的“噪音”。

(4) 啟發式決策模型與計算式決策模型的融合。長期以來, 計算式的決策模型(如決策場模型與馬爾科夫決策模型)由于其較為復雜的數學結構, 往往不能為大多數研究者所理解; 而計算式決策模型的研究者, 在其構建模型的過程中, 往往將重心放在數學結構上, 從而忽視了與其相關的啟發式決策模型。通過本研究的結果, 可以看出, 啟發式決策模型與計算式決策模型能夠很好地融合, 通過啟發式的思想對計算式的模型進行改進, 不僅能夠解決計算式模型中存在的一些困難, 而且能使啟發式的思想以較為客觀的數學形式展現出來, 讓其具有量化解釋問題的能力。因此, 啟發式決策模型與計算式決策模型的融合, 具有重要的理論意義與廣闊的發展前景。

致謝：作者感謝兩位匿名審稿專家對本文提出的嚴謹而富有建設性的意見。

Baron, J. (2007).. Cambridge University Press.

Bi, Y. L., Li, S. (2007). A comparison between two models of bounded rationality: Equate-to-differentiate and priority heuristic approaches.(4), 682?688.

[畢研玲, 李紓. (2007). 有限理性的"占優啟發式"和"齊當別"決策模型的作為——當Allais悖論杠桿撬動了期望效用理論.(4), 682?688.]

Blanco, M., Engelmann, D., Koch, A. K., & Normann, H. T. (2014). Preferences and beliefs in a sequential social dilemma: A within-subjects analysis., 122?135.

Blutner, R., Pothos, E. M., & Bruza, P. (2013). A quantum probability perspective on borderline vagueness.(4), 711?736.

Bruza, P. D., Wang, Z., & Busemeyer, J. R. (2015). Quantum cognition: A new theoretical approach to psychology.(7), 383?393.

Busemeyer, J. R., & Bruza, P. D. (2012).. Cambridge University Press.

Busemeyer, J. R., & Johnson, J. G. (2008). Micro-process models of decision making.Cambridge University Press,(pp.302?321).

Busemeyer, J. R., Matthew, M. R., & Wang, Z. (2006).Paper presented at the Proceedings of the Annual Meeting of the Cognitive Science Society.

Busemeyer, J. R., & Townsend, J. T. (1993). Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment.(3), 432?459.

Busemeyer, J. R., & Wang, Z. (2015). What is quantum cognition, and how is it applied to psychology?(3), 163?169.

Busemeyer, J. R., Wang, Z., Khrennikov, A., & Basieva, I. (2014). Applying quantum principles to psychology.(T163), 014007.

Busemeyer, J. R., Wang, Z., & Lambert-Mogiliansky, A. (2009). Empirical comparison of markov and quantum models of decision making.(5), 423?433.

Busemeyer, J. R., Wang, Z. J., & Pothos, E. (2015). Quantum models of cognition and decision.. Oxford University Press, (pp. 369?389).

Busemeyer, J. R., Wang, Z., & Townsend, J. T. (2006). Quantumdynamics of human decision-making.(3), 220?241.

Croson, R. T. A. (1999). The disjunction effect and reason- based choice in games.(2), 118?133.

Denolf, J., Martínez-Martínez, I., Josephy, H., & Barque- Duran, A. (2017). A quantum-like model for complementarity of preferences and beliefs in dilemma games., 96?106.

Festinger, L. (1957).(Vol. 2). Stanford university press.

Gigerenzer, G., & Todd, P. M. (1999).. Oxford University Press.

Kahneman, D., & Tversky, A. (2013). Prospect theory: An analysis of decision under risk.(pp. 99?127): World Scientific.

Kubovy, M., Rapoport, A., & Tversky, A. (1971). Deterministic vs probabilistic strategies in detection.(5), 427?429.

Li, S. (2005). Choice reversals across certainty, uncertainty and risk: The equate-to-differentiate interpretation.(4)427–433.

[李紓. (2005). 確定、不確定及風險狀態下選擇反轉:“齊當別”選擇方式的解釋.(4), 427?433.]

Li, S. (2016).. Shanghai: East China Normal University Press.

[李紓. (2016).. 上海: 華東師范大學出版社.]

Li, S., Bi, Y. L., Liang Z. Y., Sun, Y., Wang, Z. J., & Zheng, R. (2009). Bounded or unbounded rationality? The implication of equate-to-differentiate theory in economic behavior.(5), 143–154.

[李紓, 畢研玲, 梁竹苑, 孫彥, 汪祚軍, 鄭蕊. (2009). 無限理性還是有限理性?——齊當別抉擇模型在經濟行為中的應用.(5), 143?154.]

Li, S, & Taplin, J. (2002). Examining whether there is a disjunction effect in prisoner's dilemma games.(1), 25–46.

Li, S., Taplin, J. E., & Zhang, Y. C. (2007). The equate-to- differentiate’s way of seeing the prisoner’s dilemma.(6), 1395?1412.

Payne, J. W., & Bettman, J. R. (2004). Walking with the scarecrow: The information-processing approach to decision research., 110?132.

Pleskac, T. J., Diederich, A., & Wallsten, T. S. (2015). Models of decision making under risk and uncertainty.. Oxford University Press, (pp. 209?231).

Pothos, E. M., & Busemeyer, J. R. (2009). A quantum probability explanation for violations of ‘rational’decision theory.,(1665), 2171?2178

Savage L J. (1954).. New York: Wiley.

Shafir, E., & Tversky, A. (1992). Thinking through uncertainty: Nonconsequential reasoning and choice.(4), 449?474.

Smith, J. M. (1982).. Cambridge University Press.

Stevenson, M. K., Busemeyer, J. R., & Naylor, J. C. (1990). Judgment and decision-making theory.Consulting Psychologist Press.

Su, R. K. (2002). Higher Education Press

[蘇汝鏗. (2002).. 高等教育出版社.]

Townsend, J. T., Silva, K. M., Spencer-Smith, J., & Wenger, M. J. (2000). Exploring the relations between categorization and decision making with regard to realistic face stimuli.(1), 83?105.

Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases.(4157), 1124?1131.

Tversky, A., & Kahneman, D. (1981). The framing of decisions and the psychology of choice.(4481), 453?458.

Tversky, A., & Shafir, E. (1992). The disjunction effect in choice under uncertainty.(5), 305?310.

Wang, Z., & Busemeyer, J. R. (2016). Interference effects of categorization on decision making., 133? 149.

Wang, Z. J., Li, S. (2008). The disjunction effect in decision making.(4), 513– 517.

[汪祚軍, 李紓. (2008). 行為決策中出現的分離效應.(4), 513?517.]

Xin, X. Y., Xu, C. H., Chen, H. Y., Li, Y. (2018). Quantum models for decision making.,(8), 1365?1373.

[辛瀟洋, 徐晨虹, 陳宏玉, 李瑛. (2018). 一種新決策模型——量子決策模型.,(8), 1365?1373.]

Yearsley, J. M. (2017). Advanced tools and concepts for quantum cognition: A tutorial.,, 24?39.

[1] 在量子決策模型中, 通常將薛定諤方程中的普朗克常數設定為1。方程中,表示虛數單位,表示自然常數,表示決策過程所需的時間, 但并非客觀的絕對時間。

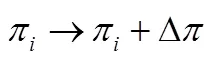
Quantum decision-making model based on equate-to-differentiate method: Explanation for the disjunction effect in prisoner’s dilemma

XIN Xiaoyang; LI Ying; BI Yanling; YAN Bihua

(School of Psychology, Shaanxi Normal University & Key Laboratory of Behavioral and Cognitive Neuroscience of Shaanxi Province, Xi’an 710062, China)

One of the most puzzling findings in decision research field is the disjunction effect. Several studies demonstrate that the disjunction effect exists in a two-person prisoner’s dilemma game. This effect violates the sure-thing principle and cannot be explained by classical decision-making models. During the recent decade, quantum decision making models have been established on the basis of the mathematical structure and methodologies of quantum mechanics. Owing to their special theoretical structures, quantum decision-making models are well suited for explaining the disjunction effect, although these models continue to encounter difficulties.

This study aims to overcome the difficulties in existing quantum decision-making models by developing a modified model. To achieve this goal, the deficiencies of the previous models were analyzed. We concluded three deficiencies: 1) Although previous quantum decision-making models can account for the disjunction effect, they can also obtain findings that defy the experimental results and common sense. 2) They cannot explain the disjunction effect with large values in certain experiments (e.g., the experiment of Shafir & Tversky, 1992). 3) They cannot properly illustrate the relationship between the utility of decision maker’s pay off and the scale of the disjunction effect.

The reasons for these difficulties were investigated. An important reason is that previous quantum decision-making models ignore that the decision maker may consider another’s pay off based on different decision conditions. Another reason is the over-simplicity of the utility function. With the above analyses as basis, we adopted the equate-to-differentiate method to rebuild the quantum decision-making model. In this new model, whether the decision maker considers another’s pay off or not based on a specific decision condition is determined with the equate-to-differentiate method. In addition, the utility function is redefined by value function and hyperbolic tangent transformation.

Results revealed that the new quantum decision-making model overcomes the difficulties in previous quantum decision-making models. The proposed model is an integration of heuristic and computational or mathematical models. This ideal model integration deserves much attention and has good theoretical significance and application prospects.

quantum; decision-making; equate-to-differentiate; disjunction effect; prisoner’s dilemma

2018-05-30

* 陜西省科技統籌創新工程計劃項目(2015KTZDSF02-02)以及陜西師范大學教師教育研究項目(JSJY2018002)。

李瑛, E-mail: liying@snnu.edu.cn

10.3724/SP.J.1041.2019.00724

B841.2; C934