凸函數在數量經濟學中的應用

張志明 湖北科技學院數學與統計學院

自從21世紀伊始凸函數理論得以成立之后，它作為核心的理論，在各種數學研究中都被有效地運用。在目前普遍適用的高等數學的教科書里，全部有著凸函數的相關概念解釋。然而因為不同書籍的不同作用，對它的解釋也有著各種差別。當前，由于數學被普遍運用于經濟學范疇內，而使得數學從冷門學科一躍成為炙手可熱的學科。其中，數量經濟學主要通過對數學學科知識的運用來尋求答案，但是數理經濟學研究中相關的一些函數普遍具備凸性，這就決定了凸函數在其中的普遍運用，它能夠對企業探討財務資源的有效配備提供助益，從而幫助企業的利益達到最大。

一、凸函數的概念

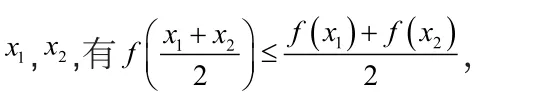
則稱f(x)為I上的凸函數[1]。

定義2 若在定義I上成立不等式

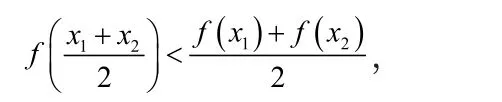
則稱f(x)是I上嚴格的凸函數[2]。

二、關于凸函數的幾個重要不等式

（一）Jensen不等式

定理1 （凸函數的基本不等式）設?(x)是間I上的凸函數，則對I中n個數成立不等式，當僅當時等號。

（二）Hadamard不等式

兩邊積分可得

三、函數凸性在數量經濟學中的應用

在市場經濟運行之時，生產商的主要要求就是，如何利用盡可能少的物資和成本，取得盡可能大的市場效益和利潤。他們會通過預估行為，構造一個效益、成本、價格三者相關的函數公式，之后再通過求取凸函數的極限值，來達到效益最優化、支出最小化的目的。通過對二次倒數求導，來判定函數的凹凸性，確定了函數的凹凸性之后，我們就可以根據凹凸函數的性質，進而計算出最大值和最小值。這是我們利用函數凹凸性的進行經濟決策的基礎。在實際的生活中，我們對于利用函數的凹凸性，尤其是凸函數進行經濟評估時，不是簡單的通過計算就可以得到最大值的。我們更需要的是首先對經濟問題進行分析，從而在這個過程中提煉出來一種經濟學模型來。然后才是對模型進行函數上的數學計算和分析。

（一）利潤最大問題

在任何的經濟活動中，利潤是不可缺少的部分，如何尋找一種利潤最大化的方案是我們所要解決的。其中成本函數與生產函數之間也有一種函數關系。當這種函數為凸函數時，對其利潤最大值的計算就可以利用凸函數的性質去求解。

例1假設某一個產品，其需求量的函數可以用Q=12000-80P（P的單位為元，表示產品單價）來表示，而該產品總的生產成本為C=25000+50Q，而銷售后每一件產品的稅費為2元，請求出產品獲取最大利潤時的單價和最大利潤額。

對于如何尋求效益的最大化，首先需要尋找與效益相聯系的生產要素的函數關系，先通過一階導數尋找其穩定點，然后繼續求其二階導數，通過這個導數辨別利潤函數是不是凹函數，通過辨別如果是凹函數的話，那么就可以從中選取出最大的數值，也就是最大化的效益。這樣一來，復雜的經濟現象就變成了數學理論中經常被使用到的函數，把尋求經濟效益的最大化轉換成一般的凸函數求極值的問題，這是對數學知識的更好的應用，也是數學對經濟問題的有效解決

（二）成本最小問題

下面看一下成本最小問題。

例2 現在需要制作一個固定容量為500cm3的罐子，其形狀規定為圓柱形，請問最節省制作材料的底面半徑值。

解： 設飲料罐的高為h，底面半徑為r，則表面積

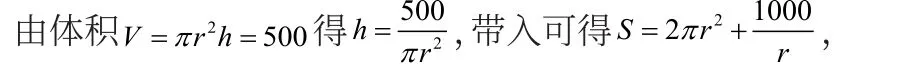
如果接下來要尋求支出成本最小化，同樣通過構造一個函數關系式，運用定理四來辨別這個公式是不是凸函數，如果確認是凸函數，那么就可以從中尋找到最小的數值，也就找到了最小的成本。經濟活動中靈活地運用數學方法，能夠有效地解決復雜問題，并促進經濟發展。

（三）最佳庫存問題

在企業的整個運營當中，必須要對庫存的數量進行一個很好的衡量。如果庫存太少，那么很可能在市場需求量大的時候，失去搶占市場的能力。但是如果庫存太多，又有可能導致資金的壓力或者商品積壓太多的問題。如果一個企業希望自己的運營效果較好，那么管理者首先需要決定產品的庫存數量，這其中包括了什么時候對庫存進行補充、補的數量又是多少等問題。這個方面也能夠利用函數關系，求取凸函數的極限值，從而有效解決相關庫存難題。

例3 一個商品的年度總銷售額為10萬件，如果設定這些商品是在不同時間進行生產的，而每件商品的生產成本是100元，而生產企業中的平均庫存量是生產批量的一半，而每一個商品在倉庫放一年，需要支出成本零點零五元。那么，現在來測算，如果令每一年的生產成本與支出庫存費用總數最小化，每次應該生產多少數目的產品。

解： 設每年的生產準備費與庫存費之和為W，批量為x，則

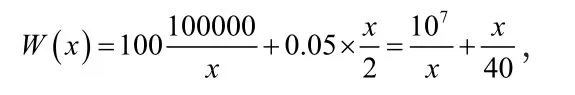
總結來說，在求解關于經濟問題的最優化時我們可以把它看成是數學中的求最值問題。步驟為：

（1）對經濟問題中的目標函數與相關聯因素的函數關系進行準確分析；

（2）對函數關系式求一階導數，求出穩定點；

（3）對函數進行二階求導，根據凹凸性去確定函數特性。

（4）當知道問題有極值存在時，接下來判斷極值點是否是唯一的，當唯一時則函數在該駐點有極值，這就解決了經濟問題中的最優化問題了。