安多主要藏傳佛教寺院旅游路徑的優(yōu)化問題研究

加華多杰，張海東，熊良林

?

安多主要藏傳佛教寺院旅游路徑的優(yōu)化問題研究

加華多杰1，張海東1，熊良林2

（1. 西北民族大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院，甘肅 蘭州 730030；2. 云南民族大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院，云南 昆明 650500）

以安多主要寺院為例，探討、分析和設(shè)計安多主要藏傳佛教寺院旅游路線與路線優(yōu)化問題，首先確定旅游寺院，然后建立規(guī)劃問題的旅游路線優(yōu)化設(shè)計模型，將經(jīng)典TSP問題轉(zhuǎn)移到時間矩陣求解和最優(yōu)化原理，使其問題簡便化，然后運用Lingo編寫程序運行，得出最優(yōu)路線。結(jié)果說明所規(guī)劃的模型、運行算法可解決多種路線優(yōu)化設(shè)計，為更多寺院游客、朝拜者及想要了解藏民族文化的人士提供最優(yōu)路線。

旅游；最優(yōu)路線；規(guī)劃問題；寺院；Lingo

隨著社會的發(fā)展，人們生活水平的提高，旅游成為人們熱衷的活動之一。而為了不受時間的束縛，自駕游成了大多數(shù)旅游者的選擇。對于自駕游的旅客而言，如何安全、經(jīng)濟、充分地觀光目的地，并按計劃時間快樂地返回到家才是最重要的。路徑優(yōu)化涉及社會許多領(lǐng)域。對路徑優(yōu)化的研究成果頗多，如2015年Qiu等人研究了多中心、多種商品，物流應(yīng)急受影響問題，提出建立時間最大化的目標(biāo)函數(shù)的非線性規(guī)劃模型，經(jīng)過多條路評價尋優(yōu)得到最優(yōu)路線[1]。同年許麗霞等人跟據(jù)最優(yōu)化原理和動態(tài)規(guī)劃原理建立整數(shù)規(guī)劃模型和逐步轉(zhuǎn)化模型算法，通過比較得出逐步轉(zhuǎn)化模型算法具有可操作性[2]。2016年袁光輝等人以西安市出發(fā)為例研究旅游路線規(guī)劃問題，提出建立旅游路線綜合規(guī)劃模型，利用Matlab編程基于遺傳算法進行求解得出最優(yōu)路線[3]。2016年Wang等人分析了時間和路線建立最優(yōu)路徑、最小成本模型，使用線性規(guī)劃方法、Matlab軟件得出優(yōu)化路線[4]。楊麗馨構(gòu)建了一種自駕游旅游模型，利用求解VRP的蟻群算法得出理想結(jié)果[5]。本文以安多主要寺院為例進行路徑研究，解決安多主要藏傳佛教各寺院旅游的最優(yōu)路線問題。假定有一名或多名到安多地區(qū)青海、甘肅和四川三個省的九所藏傳佛教寺院：塔爾寺、佑寧寺、拉卜楞寺、廣惠寺、隆務(wù)寺、夏瓊寺、色達寺、卻藏寺和賽宗寺旅游。對此應(yīng)考慮如何從一個景點到另一個景點的路徑、時間和成本最優(yōu)，從而設(shè)計出最優(yōu)旅游線路，利用時間矩陣算法和最優(yōu)化原理在Lingo程序運行求解，使其計算快速簡單化。

1 問題分析

1.1 問題提出及假設(shè)

假設(shè)所選定寺院全部可旅游、游客一路安康并沒有特別儀式，只根據(jù)行程選擇旅游地點、不出現(xiàn)車輛故障和交通事故，規(guī)劃以下兩類問題[3]：

（1）游客旅游時間不限，游完九個寺院，使得旅游路程最短的線路設(shè)計；

（2）游客旅游路程不限，游完九個寺院，使得旅游時間最短的線路設(shè)計。

1.2 符號說明

ij——表示第個寺院到第個寺院的距離。

——表示總花費時間。

——表示總距離。

i——表示各寺院。

ij——表示第寺院和第寺院的0-1變量。

1——表示乘車總時間。

2——表示在寺院朝拜時間。

1.3 相關(guān)數(shù)據(jù)

根據(jù)寺院知名度及規(guī)模選擇寺院，通過網(wǎng)絡(luò)查詢得到寺院間距離、路途耗費時間及寺院旅游時間[6]。結(jié)果列于表1至表3。

表1 寺院個數(shù)及旅游時間

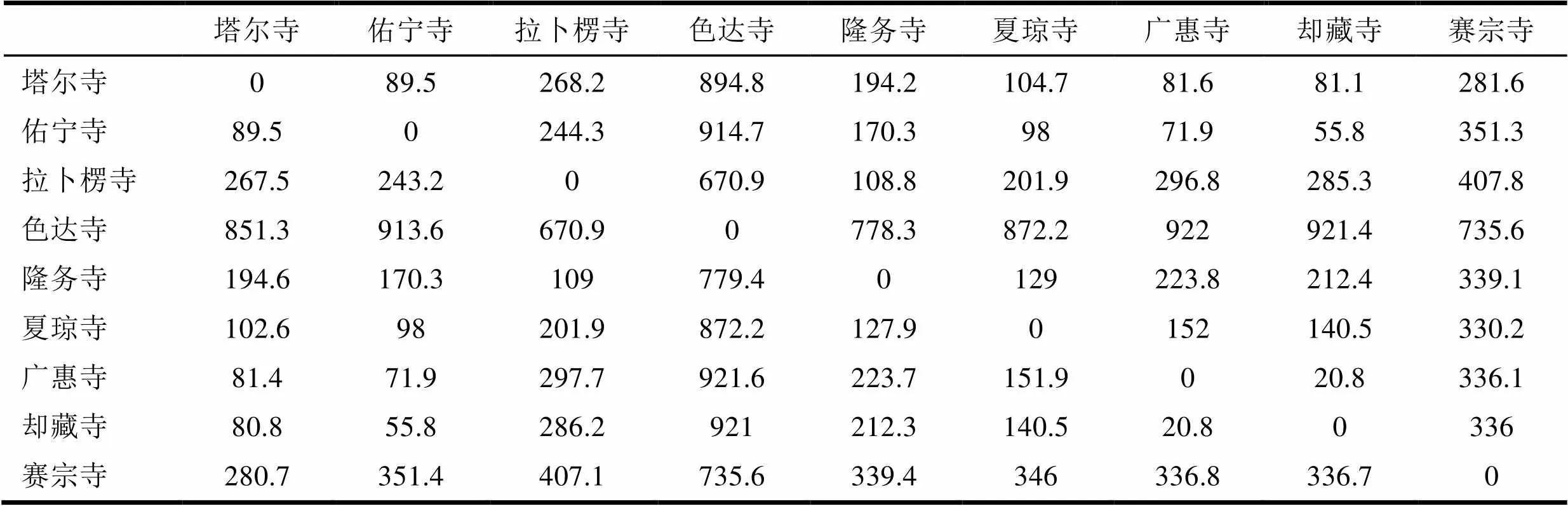
表2 各寺院間的距離（單位：km)

表3 各寺院間的路途時間（單位：h）

（續(xù)表3）

2 建立模型及解決問題

2.1 分析

因為

旅游總時間=乘車時間+在寺院觀光時間

所以，得到目標(biāo)函數(shù)[1]：

旅游路途中所需的總時間[4]：

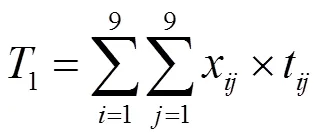
其中，t表示游客從第寺院到第寺院的路途時間，而x是判斷朝拜者從第寺院到第寺院的0-1變量。

在寺院的旅游時間[4]：

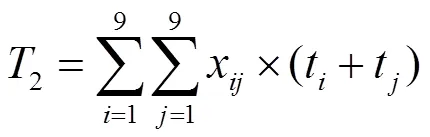
（1）旅游寺院數(shù)約束[7]

根據(jù)假設(shè)以及整個旅游路線是環(huán)形，游客最后還要回到湟中縣，所以要旅游的寺院數(shù)為9，因此旅游的寺院約束為：

（2）0-1變量約束[3]

將所有寺院連成一個圈，把每個寺院看成是圈上的一個點。對于每一個點，入邊只允許最多一條，出邊也只允許最多一條，并且一旦有一條邊進入就要有一條邊出去。因此可得約束：

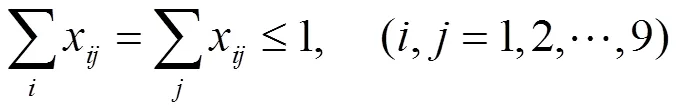
綜上，可得：

;

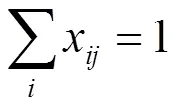
由此可得約束：

以上兩個約束是為了不出現(xiàn)兩個以上環(huán)形回路，保證有且僅有一條環(huán)形路線。

2.2 模型建立

根據(jù)上面的分析，得到總的模型：

其中，

2.3 模型求解及結(jié)果分析

通過路線查詢，得到d的具體值及通常情況下的t，利用Lingo進行編程。在編程中為了不出現(xiàn)兩個以上環(huán)形回路，需設(shè)計一個變量。Lingo程序編程及運行結(jié)果如圖1所示。

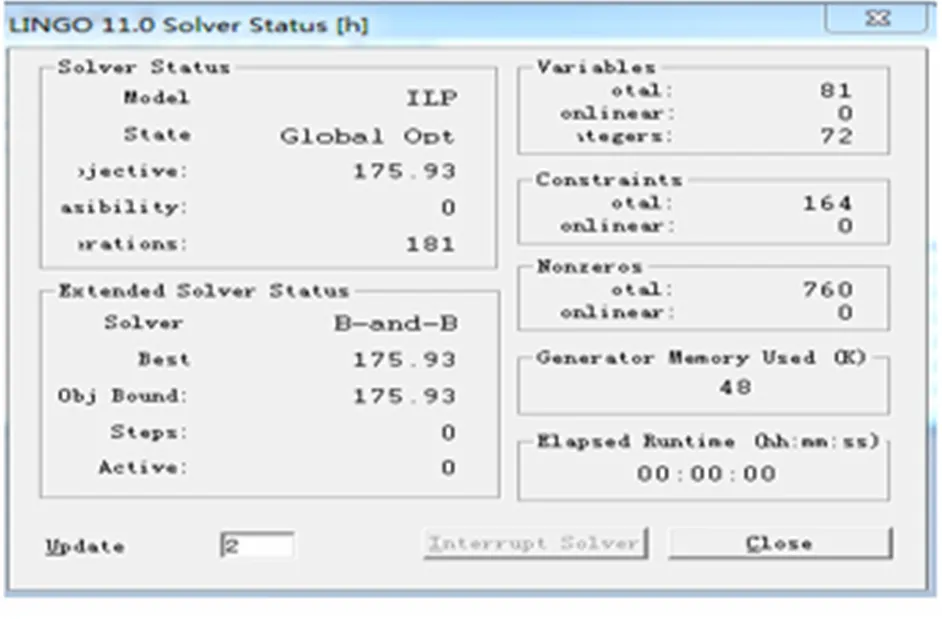
圖1 耗費時間最少的模型Lingo運行結(jié)果

根據(jù)運行程序得到最優(yōu)路線：

對應(yīng)總時間為=175.93 h，即7.33 d。

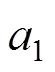
綜上得知：可以用矩陣表示a到a的距離，矩陣中的每一個元素為d。

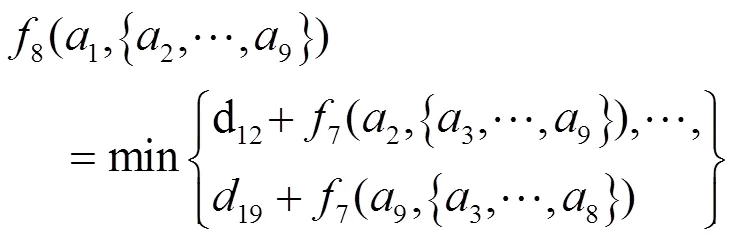
采用Lingo程序編程求解，Lingo程序編程及運行結(jié)果如圖2所示。

根據(jù)運行得到最優(yōu)路線：

即：塔爾寺廣惠寺卻藏寺佑寧寺夏瓊寺隆務(wù)寺拉卜楞寺色達寺賽宗寺，對應(yīng)最短距離D=2 180.3 km。

3 結(jié)束語

[1] B J Qiu, J H Zhang, Y T Qi, Y Liu. Grey-theory-based optimization model of emergency logistics considering time uncertainty[J]. PLOS ONE, 2015, 10(9):e0139132.

[2] 許麗霞,徐琪,范丹丹.基于兩種模型的整車物流運輸計劃問題研究[J].數(shù)學(xué)的實踐與認(rèn)識,2015,45(22):213- 220.

[3] 袁光輝,謝科,鄧林勝,等.旅游路線動態(tài)規(guī)劃問題研究——以西安市出發(fā)為例[J].數(shù)學(xué)的實踐與認(rèn)識,2016, 46(15):125-133.

[4] 李進立,韋程東,劉廣會,等.旅游路線規(guī)劃問題[J].廣西師范學(xué)院學(xué)報(自然科學(xué)版),2016,33(1):30-38.

[5] 楊麗馨.基于混合蟻群算法的“多日游”路線優(yōu)化問題[J].唐山師范學(xué)院學(xué)報,2013,35(5):37-40.

[6] 百度地圖[EB/OL].http://ditu.baidu.cn/, 2014-12-10.

[7] W Bi, Q Zhou, L Liu, C Sun. Study on mathematical model of urban distribution system optimal rush- maintain path[J]. International Conference on Power System Techno, 2002, 2(2): 1077-1081.

[8] Smelyakov S V, Stoyan Yu G. A mathematical model of certain problems of optimization on paths[J]. Engrg. Cybernetics, 1981, (4): 180-188, 223.

On the Optimal Path of Tourism in Andomain Tibetan Buddhism Temple

JIA-hua Duo-jie1, ZHANG Hai-dong1, XIONG Liang-lin2

(1. School of Mathematics and Computer Science, Northwest Minzu University, Lanzhou 730030, China; 2. School of Mathematics and Computer Science, Yunnan Minzu University, Kunming 650500, China)

In this paper, the temple of Ando was taken as an example to discuss, analyze and design the best Tibetan Buddhist monasteries in Ando route problems. Firstly, a tourist route optimization design model based on the planning issue was established. Transfer the classical TSP problem to the time matrix solution and optimization principle to simplify the problem. Then use Lingo to write the program to get the best route. The result shows that the acquired data, models and algorithms can solve a variety of route optimization designs and provide the best route for more tourists, pilgrims who want to understand the Tibetan culture.

tourism; the optimal route; planning issues; temple; Lingo

F59

A

1009-9115(2019)03-0022-05

10.3969/j.issn.1009-9115.2019.03.007

國家自然科學(xué)基金項目（11461082，11601474），甘肅省自然科學(xué)基金項目（1606RJZA003），甘肅省高等學(xué)校科研項目（2016B-005）

2018-07-31

2019-03-11

加華多杰（1992-），男，藏族，青海海東人，碩士研究生，研究方向為模糊系統(tǒng)理論及其應(yīng)用、最優(yōu)化理論。

（責(zé)任編輯、校對：趙光峰）