人字形花紋輪胎壓實土壤垂直應力分布規律研究

姜春霞，魯植雄，Shrini K. Upadhyaya，陳 豐

（1. 南京農業大學工學院，南京 210031；2. 美國加州大學戴維斯分校，加州戴維斯 95616；3. 安徽科技學院機械工程學院，鳳陽 233100）

0 引 言

當荷載施加在土壤上導致土壤失去內部間隙，就會發生壓實。土壤壓實對土壤物理性質有著很大的影響[1]，土壤壓實程度取決于車輛施加在土壤上的應力以及土壤-輪胎相互作用接觸面內的應力分布[2]。此外，土壤垂直應力分布在很大程度上是土壤表面應力模式的函數[3-4]，受土壤物理特性的影響較小[5-6]。Keller等[7]指出通過實際垂直應力分布（而不是理論接觸面積應力分布）來精確預測土壤接觸面的垂直應力是非常重要的。對于農用車輛，可以通過減少載荷或增加接觸面積來減少土壤壓實。

很多研究學者通過假設土壤表層垂直應力分布是均勻的來研究輪胎在高壓下的土壤垂直應力分布。但是美國土壤動力學研究中心 Way等[8]的研究表明，對于充氣氣壓為40 kPa的輪胎，垂直應力主要集中在輪刺中心處或者輪胎胎面邊緣，而不是輪胎中心處。此外，Gysi等[9]的研究表明采用導致輪胎邊緣垂直應力為峰值而輪胎中心處的垂直應力為最小值時的載荷值來建立土壤壓實模型更合理。Arvidsson等[10]也指出，在他們的測試中，垂直應力的峰值發生在輪胎邊和和中心線之間，垂直應力分布并不是均勻的。

土壤-輪胎之間的力是通過輪胎的胎體進行傳遞的，集中在輪胎的胎面上[11]，土壤-輪胎接觸面垂直應力分布的形式會受到胎壓的影響。Arvidsson等[12]指出平均土壤垂直應力和胎壓幾乎相等，但是Koolen等[13]卻指出由于輪胎硬度的存在，平均垂直應力是胎壓的 1.2～1.3倍。對于高變形的輪胎，低壓下垂直應力分布會更加平坦，邊緣胎體剛度的影響也會更加明顯。然而，Alakukku等[14]通過試驗卻發現平均垂直應力小于胎壓。

大量的研究涉及了胎壓對土壤垂直應力的影響，而很少有研究探討載荷和輪胎行駛速度對垂直應力的影響。Burt等[15]發現，對于松軟地面，動荷載增加，土壤-輪胎接觸面垂直應力也會增加。Schj?nning等[16]開發了一種逐步計算的方法，該方法可通過輪胎載荷的數值估算土壤垂直應力。

土壤-輪胎接觸面垂直應力的測試方法主要有將傳感器埋設在輪胎表面[17-18]和埋設在土壤內部[19-20]，其中傳感器安裝在輪胎表面是獲得精確的垂直應力最好的方法。Way等[8]將應力傳感器埋設在輪胎胎面和輪刺表面，用聲波數字轉換器確定傳感器的位置和方向。使用車輪的角位移數據來確定車輪上安裝的應力傳感器的角位置。基于土壤-輪胎接觸表層的模型[21]，假設每一個應力傳感器在應力數據有效的情況下，都和土壤有接觸。這個方法由于需要安裝聲波數字轉換器而使得費用高昂，而且接觸面上的土壤變形無法測量。Mohsenimanesh等[22]用無線電通訊系統來傳輸 6個安裝在輪胎胎面和輪刺表面的傳感器的數據，這個無線電系統離傳感器最多可以達到100 m。然而，這些都是專門開發的傳感系統，價格昂貴且測試系統復雜，鑒于此，該文將傳感器安裝在土壤內部進行應力分布的測試。

為此，該文從土壤垂直應力的影響因素著手，使用應力傳感器測試系統，在自主設計并搭建的單輪土槽試驗臺架上，進行人字形花紋輪胎壓實土壤表層垂直應力分布規律的研究，并利用多元線性回歸法建立垂直應力和影響因素之間的預測方程。希望基于建立的預測方程，在實際中通過調整影響因素的值，減小土壤垂直應力，從而減小土壤壓實，為拖拉機的通過性分析提供有力的理論分析依據。

1 材料與方法

1.1 試驗材料

1.1.1 試驗土壤

試驗為2017年4月28日-5月5日在南京農業大學工學院單輪土槽試驗臺進行，為了確定試驗區域土壤的特性一致，在土壤表層使用環刀（半徑r=30.9 mm，高度h=15 mm）采集了5個土樣，測量土壤的密度和含水量，并計算干密度，結果如表1所示，根據國際制土壤分級標準確定試驗土壤為壤土。

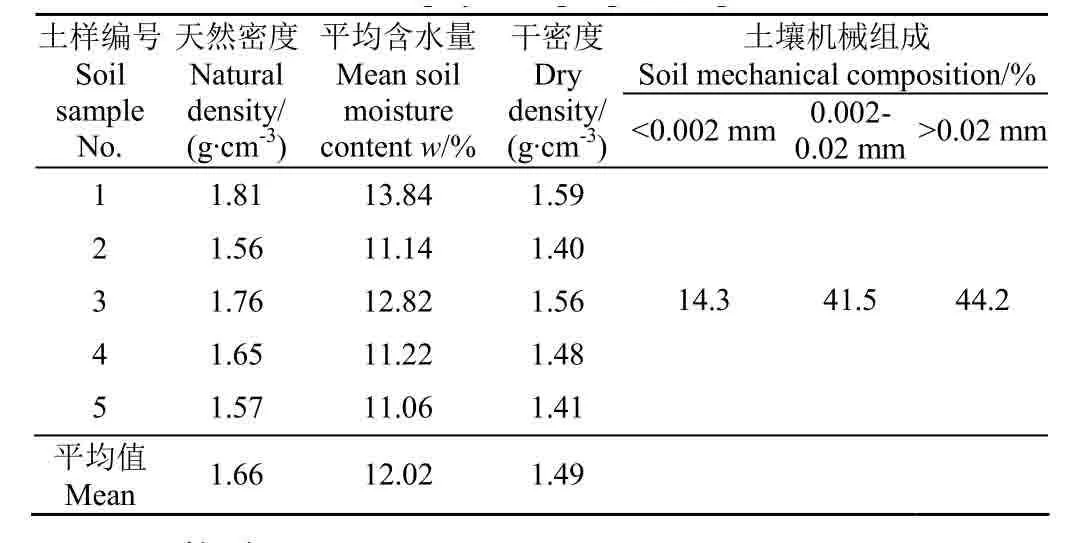
表1 土壤物理特性參數Table 1 Soil physical properties parameters

1.1.2 輪胎

為了更精確的模擬農業車輛的牽引性能，選取型號為 6.00-14的人字形花紋斜交輪胎，輪胎斷面寬度為153 mm，胎面上有 18付人字形花紋，即在寬面上布置有18付輪刺。輪胎實物如圖1。

圖1 試驗輪胎Fig.1 Test tire

1.1.3 垂直應力測試系統

垂直應力測試系統包括應力傳感器、放大器、電源、數據采集卡以及計算機。應力傳感器為由洛陽巴德電子商務有限公司生產的型號為 JHBM-50，精度為±0.05 kg的應力傳感器，圓柱形，其直徑×高度為15 mm×10 mm，材料為合金鋼。由于傳感器為敏感元件，很容易被一些大土塊壓壞，因此為了保護傳感器，設計了一個高30 mm，直徑30 mm的尼龍保護套[23]，如圖2a所示。應力傳感器通過放大器將應力信號輸出電壓放大為0～5 V，放大器產自蚌埠傳感器工程有限公司生產，型號為 BSQ-JN-Amplifier，電壓信號線性對應于應力信號0～708 kPa，由數據采集卡采集數據并傳輸到電腦上，傳感器連接方式如圖2b所示。

圖2 應力傳感器測試系統Fig.2 Test system of stress sensors

1.2 試驗方法

1.2.1 應力傳感器安裝重復性驗證試驗

為了驗證傳感器安裝的可重復性，試驗前進行了重復性驗證的試驗，將 3個應力傳感器埋設在測量區域內的任意3個位置，深度為土壤下50 mm處，以2 m/s的速度驅動車輪前進壓實這3個傳感器，由Labview采集應力傳感器的數值得到第 1組數據。挖出應力傳感器，在同樣位置重新埋設，重復3次以上試驗，得出3組數據如表2，最大誤差系數為4.14%，證明埋設傳感器的方式有效。

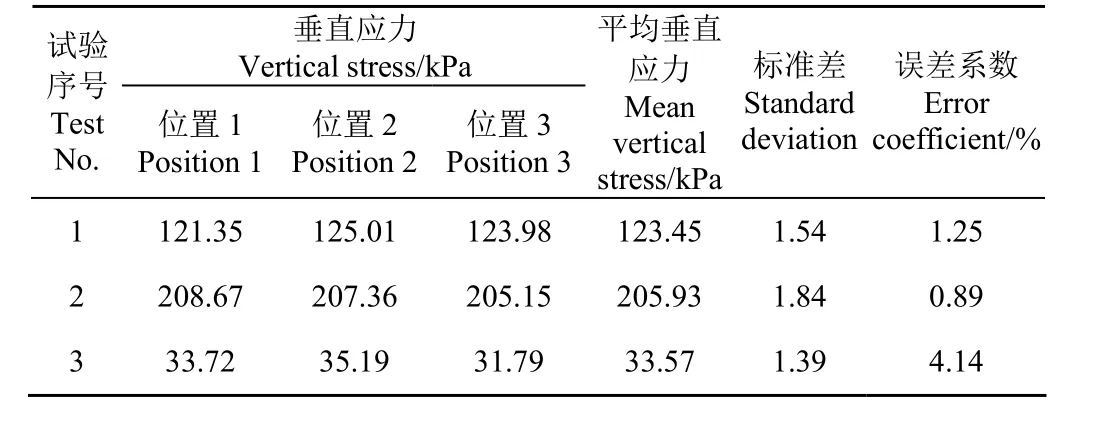
表2 應力傳感器安裝重復性試驗結果Table 2 Replication experiment of sensors installation

1.2.2 應力傳感器布置方案

輪刺右邊緣、輪刺中間、輪刺與輪胎中心線接合的位置、輪胎胎面和輪胎中心線接合的位置、輪胎胎面中間和輪胎胎面左邊緣各安裝一個傳感器，這 6個傳感器作為 1組傳感器，用來研究輪胎寬度方向的垂直應力分布；縱向上連續埋設 3組傳感器，用于測量縱向上垂直應力分布規律，用來研究輪胎前進方向的垂直應力分布。每次試驗共包含18個應力傳感器，具體布置方案如圖3所示。應力傳感器安裝之前，先移除50 mm的表層土。研究中假設輪胎沿著輪胎中心線兩邊垂直應力對稱分布[24]。

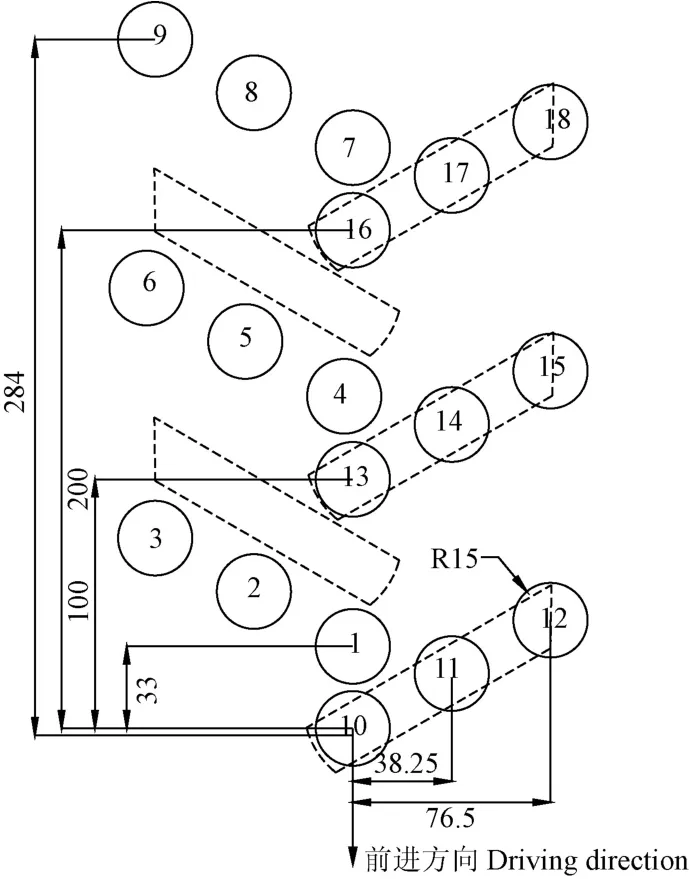
圖3 表層土應力傳感器的布置方案Fig.3 Pressure sensor arrangement scheme in topsoil

1.2.3 影響因素水平

本文主要考慮的影響因素包括胎壓、載荷和行駛速度，測量不同因素組合下的垂直應力，并對其分布規律進行分析研究。垂直應力影響因素與水平如表3。

表3 垂直應力影響因素與水平Table 3 Influence factors and levels of vertical stress

1.2.4 多元線性回歸

通常，回歸模型包括k+1個變量，即1個因變量和k個自變量（包括常數項），用n個方程來概括回歸模型[25-26]

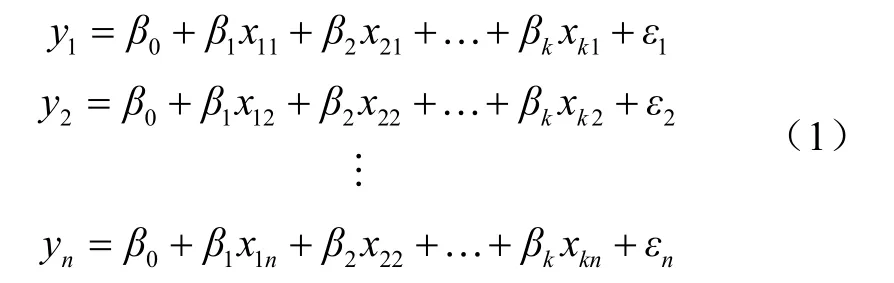
利用矩陣運算，可表示為

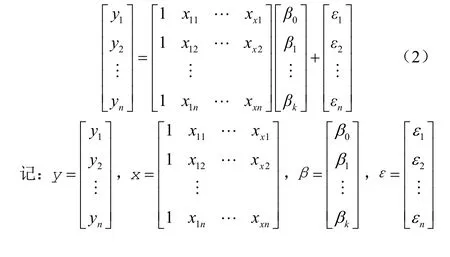
那么總體回歸模型的矩陣可以表示為

土壤表層垂直應力受到輪胎行駛速度、胎壓、載荷以及測量點位置的影響（測量點到輪胎中心處的橫向距離和縱向距離）。假設垂直應力和這 5個因素的關系類型如下

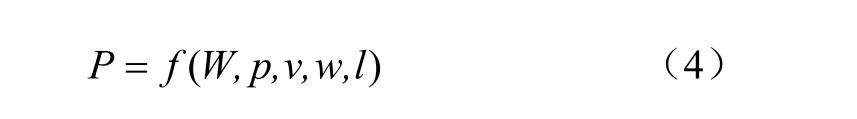
式中P為垂直應力，kPa；W為車輪載荷，kN；p為胎壓，kPa；v為輪胎行駛速度，m/s；w為測量點沿著輪胎寬度方向到輪胎中心點的橫向距離（后文簡稱橫向距離），mm；l為測量點沿著輪胎前進方向到輪胎中心點的縱向距離（后文簡稱縱向距離），mm，其中輪胎寬度方向中心線前部為正值，后部為負值。假設全因素二次方程如下

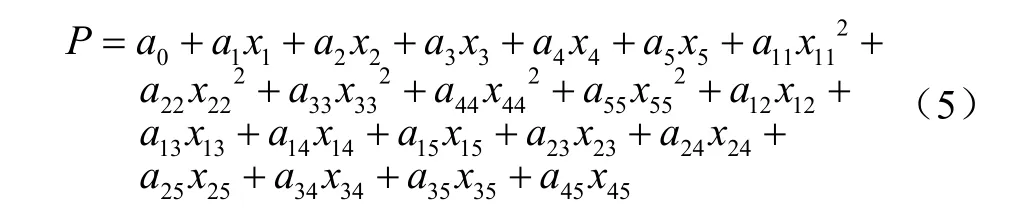
式中x1為載荷W的歸一化值并且x2為胎壓p的歸一化值并且為行駛速度 v的歸一化值并且為橫向距離w的歸一化值并且為縱向距離l的歸一化值并且為相關系數；為平均載荷，為2 kN；Wmax為最大載荷，為2.5 kN；Wmin為最小載荷，為1.5 kN；為平均胎壓，為138 kPa；pmax為最大胎壓，為207 kPa；pmin為最小胎壓，為69 kPa；為平均行駛速度，為2 m/s；vmax為最大行駛速度，為3 m/s；vmin為最小行駛速度，為1 m/s；為平均橫向距離，為0；wmax為最大橫向距離，值為76.5 mm；wmin為最小橫向距離，值為-76.5 mm；為平均縱向距離，為0；lmax為最大縱向距離，為 142 mm；lmin為最小縱向距離，為-142 mm。

所以

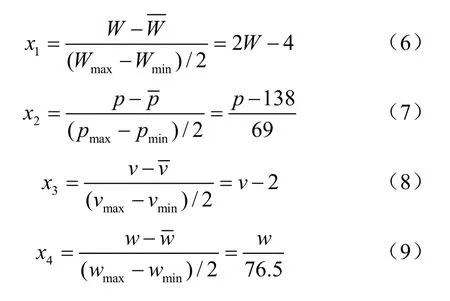
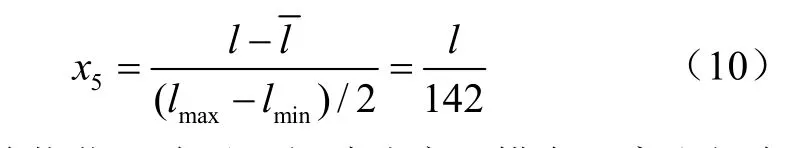
獨立參數載荷、胎壓、行駛速度、橫向距離和縱向距離值及其對應的歸一化值如表4所示。

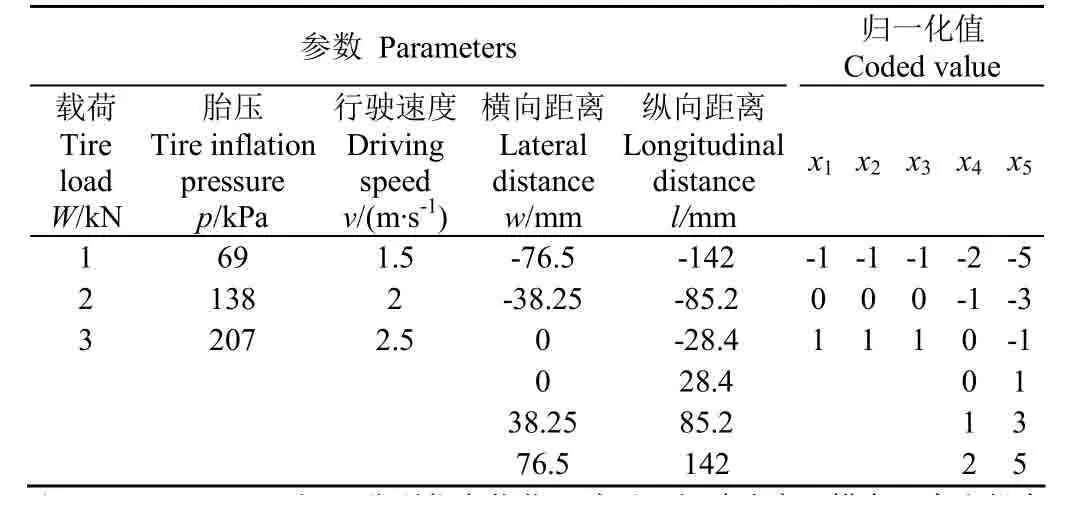
表4 獨立參數及其對應的歸一化值Table 4 Independent parameters and corresponding coded value

土壤-輪胎接觸面垂直應力受到很多因素的影響，包括土壤參數、輪胎參數以及土壤-輪胎接觸情況，所以很難建立全面的土壤-輪胎接觸面垂直應力的預測方程。目前，學者們為了方便快捷，選擇利用滑轉率作為變量建立預測方程，但在實際中縱向滑轉率和側向滑轉率受到很多因素影響，很難直接改變，即很難隨時改變垂直應力，減少壓實的效果。本文利用載荷、胎壓、行駛速度以及接觸位置作為影響因素，建立了垂直應力分布的預測方程，在實際應用中可以改變這些參數，增大接觸面積，增大驅動輪的附著力，可有效提高拖拉機的通過性。

2 結果和分析

假設輪胎橫向的垂直應力對稱，也就形成了30個數據點，通過三維分形插值的方法將原來的輪胎前進方向數據點×輪胎寬度方向數據點，也就是6×5=30個點插值2次，最終每組試驗數據點為626×527個。在3種載荷（1.5、2和2.5 kN）、3種胎壓（69、138和207 kPa）和3種行駛速度（1、2和3 m/s）下測量土壤表層的垂直應力，形成27組試驗。

2.1 土壤表層垂直應力分布的預測方程

表5是使用軟件SAS中的逆向分析法對試驗數據進行的分析結果，結果中已去掉影響較小（F＜5）的項。

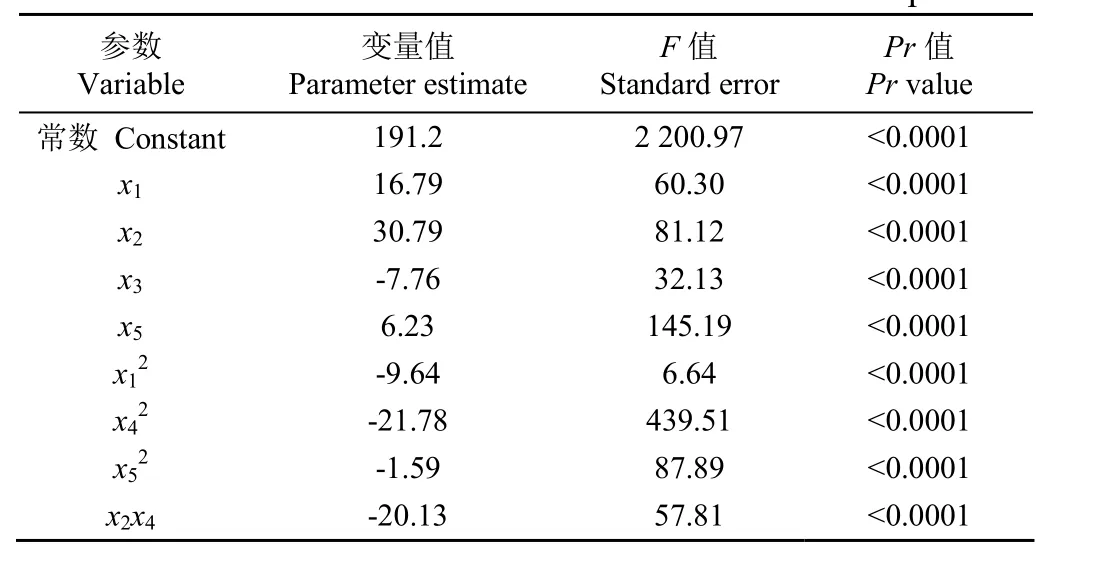
表5 影響土壤表層垂直應力分布的主要因素Table 5 Main influence factors for vertical stress in topsoil

回歸方程結果顯示

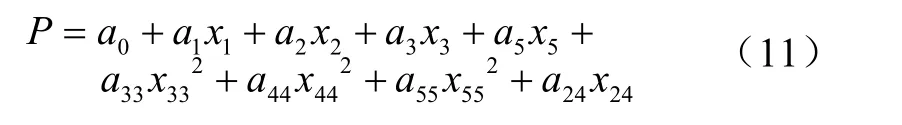
將式（6）～（10）中 x1、x2、x3、x4和x5帶入式（11）中，可得

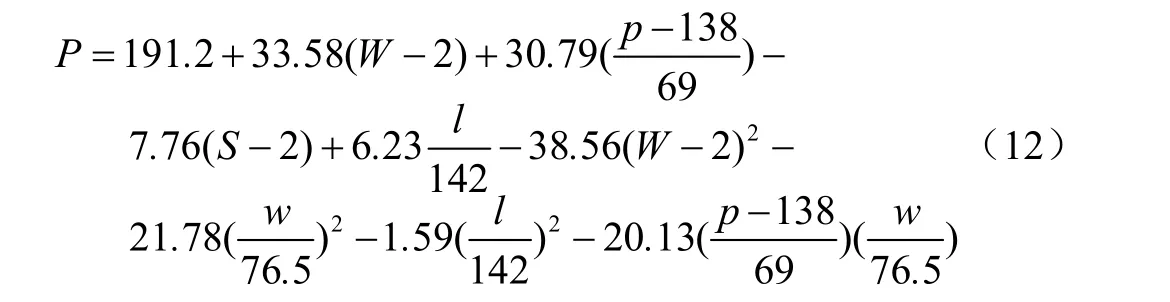
方程的確定系數 R2=85.96%，這表明方程能夠很好的表達垂直應力和載荷、胎壓、橫向距離和縱向距離的關系。由于試驗中所選的參數都是等間距的，所以選擇中心變量的模型而沒有多重共線性問題。因此，建立的預測方程有很高的預測能力。式（12）顯示，表層土中的垂直應力隨著胎壓和載荷的增加而增加，隨著行駛速度和橫向距離的增加而減小。就這些參數而言，載荷對于垂直應力的影響最大，然后依次是胎壓、行駛速度、橫向距離和縱向距離，研究結果和Gill等[27]的研究類似。

為了驗證所得預測方程的有效性，在相同土壤和輪胎狀態下，利用未用于建立預測方程的 6組試驗數據進行驗證，試驗中因素水平和試驗結果如表6。其中預測值為預測方程計算所得，實際值為實際試驗測量所得。

由表 6可得，預測值和實際值的最大誤差系數為10.59%，平均誤差系數為5.87%，證明所建立的預測方程在本文指定的土壤和輪胎狀態下具有一定的預測能力。

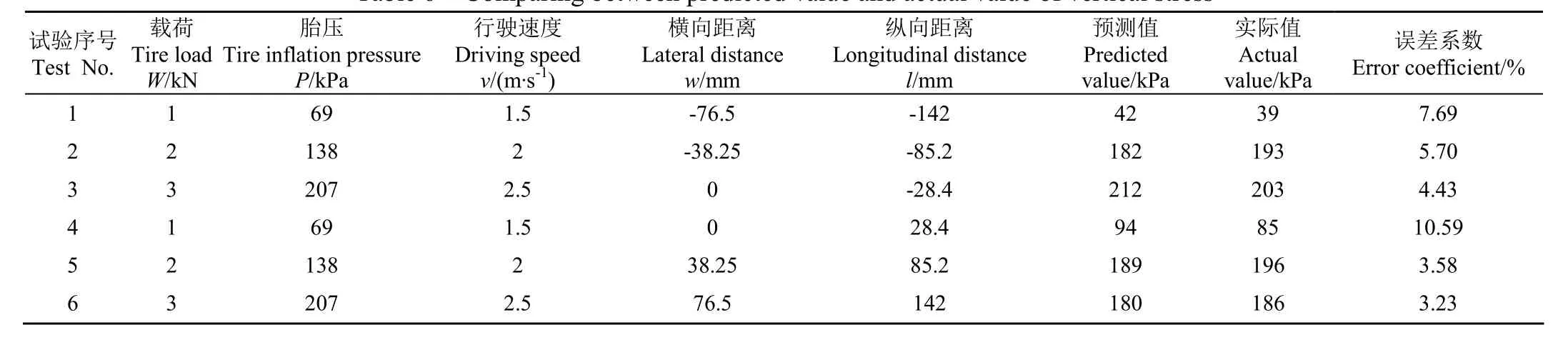
表6 垂直應力預測值和實際值對比Table 6 Comparing between predicted value and actual value of vertical stress

2.2 單因素對土壤表層垂直應力的影響

2.2.1 載荷對土壤表層垂直應力的影響

當胎壓、行駛速度和位置確定時，例如：p=138 kPa，v=2 m/s，w=0和l=0，則載荷對土壤表層垂直應力的影響規律為

式（13）顯示，對于給定胎壓、行駛速度和位置，垂直應力和載荷呈拋物線關系，如圖4所示。

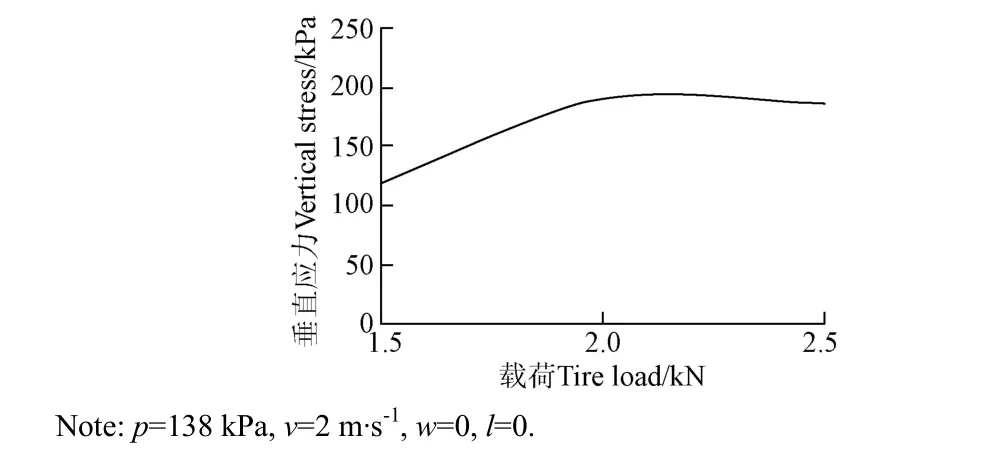
圖4 載荷對土壤表層垂直應力的影響Fig. 4 Influence of tire load for vertical stress in topsoil

2.2.2 胎壓對土壤表層垂直應力的影響

當載荷、行駛速度和位置確定時，例如：W=2 kN，v=2 m/s，w=0和l=0，則胎壓對土壤表層垂直應力的影響規律為

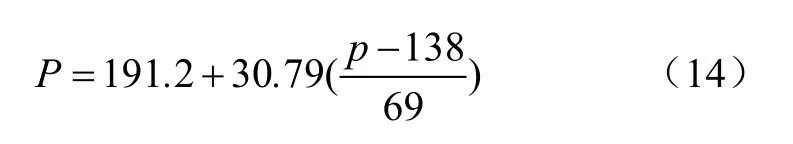
式（14）顯示，對于給定行駛速度、載荷和位置，垂直應力和胎壓呈線性關系，如圖 5所示，并且隨著胎壓的增加，垂直應力也增加。

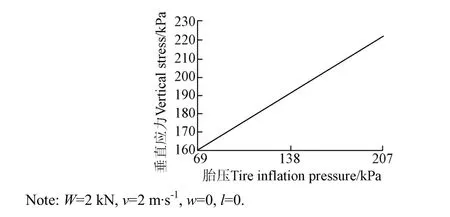
圖5 胎壓對土壤表層垂直應力的影響Fig.5 Influence of tire inflation pressure for vertical stress in topsoil

2.2.3 行駛速度對土壤表層垂直應力的影響

當載荷、胎壓和位置確定時，例如：W=2 kN，p=138 kPa，w=0和 l=0，則行駛速度對土壤表層垂直應力的影響規律為

式（15）顯示，對于給定載荷、胎壓和位置，垂直應力和行駛速度呈線性關系，如圖 6所示，并且垂直應力隨著行駛速度的增大而減小。

2.2.4 橫向距離對土壤表層垂直應力的影響

對于給定載荷、胎壓和行駛速度和縱向距離，例如：W=2 kN，p=138 kPa，v=2 m/s和l=0，則橫向距離對土壤表層垂直應力的影響規律為

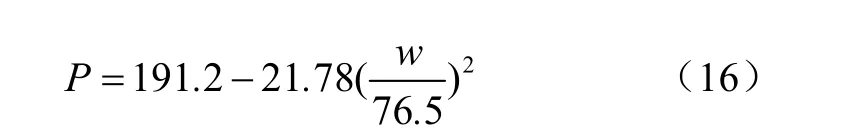
由式（16）顯示，對于給定行駛速度、載荷、胎壓和縱向距離，垂直應力和橫向距離呈拋物線關系，如圖7所示，且寬度方向隨著離輪胎中心點位置越遠，垂直應力越小。2.2.5 縱向距離對土壤表層垂直應力的影響

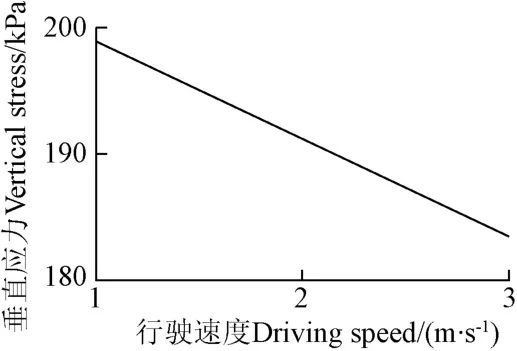
圖6 行駛速度對土壤表層垂直應力的影響Fig.6 Influence of driving speed for vertical stress in topsoil

對于給定載荷、胎壓、行駛速度和橫向距離，例如：W=2 kN，p=138 kPa，v=2 m/s和w=0，則縱向距離對土壤表層垂直應力的影響規律為

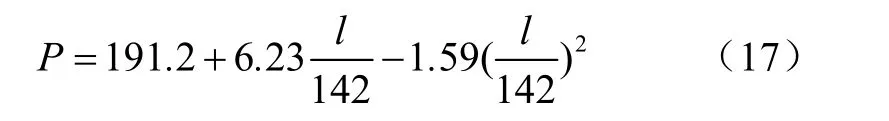
由式（17）顯示，對于給定載荷、胎壓、行駛速度和橫向距離，垂直應力和縱向距離呈拋物線的關系，如圖8所示，而且輪胎前進方向前部的垂直應力大于后部的垂直應力。

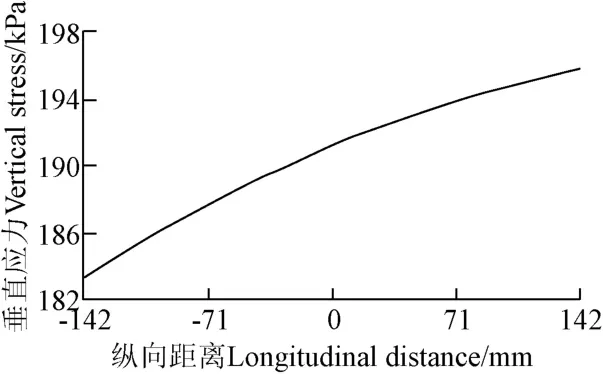
圖8 縱向距離對土壤表層垂直應力的影響Fig.8 Influence of longitudinal distance for vertical stress in topsoil

2.3 雙因素對土壤表層垂直應力的影響

2.3.1 胎壓和行駛速度對土壤表層垂直應力分布的影響

當載荷W=1.5 kN的時候，不同的胎壓和行駛速度下的垂直應力分布圖一共為9幅圖，選取其中4幅研究胎壓和行駛速度雙因素對土壤表層垂直應力分布的影響，如圖9所示。

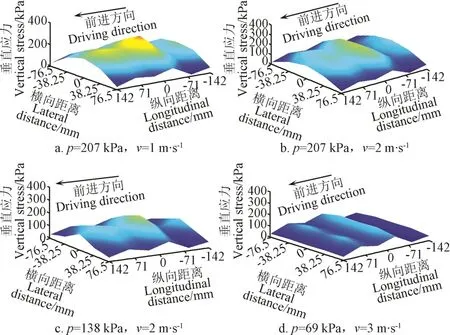
圖9 載荷為1.5 kN時不同行駛速度和胎壓下土壤表層垂直應力分布Fig.9 Vertical stress distribution in topsoil under different driving speed and tire inflation pressure when tire load was 1.5 kN

1）由圖9a可知，當p=207 kPa，v=1 m/s 時，垂直應力的值普遍較高；由圖9d可知，當p=69 kPa，v=3 m/s時，垂直應力的值普遍較低，所以農業耕作中不推薦農業車輛低速時使用高胎壓。

2）由圖9a和9c可知，當胎壓為207和138 kPa時，輪胎橫向上的垂直應力峰值出現在輪胎中心處；由圖 9d可知，當胎壓為69 kPa的時候，輪胎橫向上的垂直應力峰值出現在距離輪胎邊緣 1/4處。即當胎壓為 207和138 kPa時，土壤-輪胎接觸面垂直應力分布呈現拋物線的形態，當胎壓為69 kPa時，土壤-輪胎接觸面垂直應力分布呈現雙駝峰狀態，這與很多學者假設土壤-輪胎接觸面垂直應力在寬度方向呈現均勻的拋物線狀態有所區別。

3）由圖9a和9b可知，隨著行駛速度的增大，垂直應力反而減小，這是由于行駛速度的增大，輪胎與土壤摩擦變小，輪胎施加于土壤上的力變小，土壤下陷變小。

2.3.2 載荷和行駛速度對土壤表層垂直應力分布的影響

當胎壓p=207 kPa的時候，不同的載荷和行駛速度下的垂直應力分布圖一共有9幅，選取其中2幅研究載荷和行駛速度雙因素對土壤表層垂直應力分布的影響，如圖10所示。

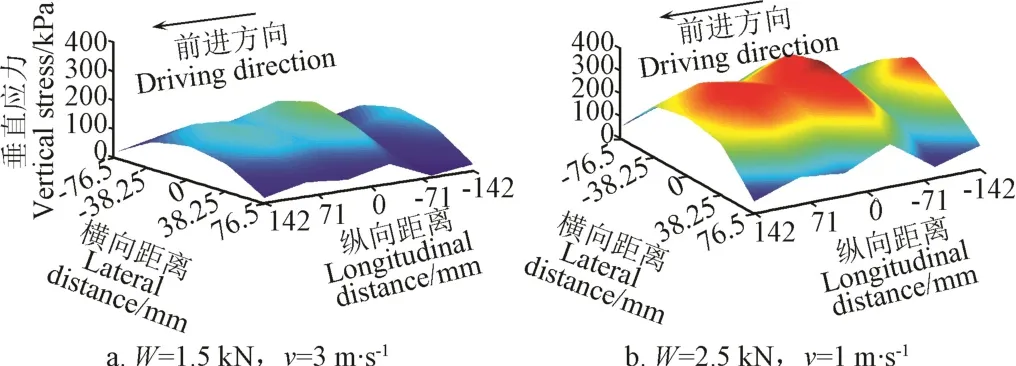
圖10 當胎壓為207 kPa時不同行駛速度和載荷下土壤表層垂直應力分布Fig.10 Vertical stress distribution in topsoil under different driving speed and tire load when tire inflation pressure was 207 kPa

由圖10a可知，當W=1.5 kN，v=3 m/s時，垂直應力的值普遍較高；由圖10b可知，當W=2.5 kN，v=1 m/s時，垂直應力的值普遍較低，所以農業耕作中不推薦農業車輛低速工作中卻附加很大的載荷。

2.3.3 載荷和胎壓對土壤表層垂直應力分布的影響

當行駛速度v=1 m/s的時候，不同的載荷和胎壓下的垂直應力分布圖一共有9幅，選取其中3幅研究載荷和胎壓雙因素對土壤表層垂直應力分布的影響，如圖11所示。

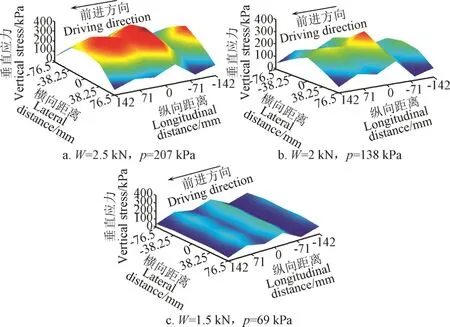
圖11 當行駛速度為1 m?s-1時不同載荷和胎壓下土壤表層垂直應力分布Fig.11 Vertical stress distribution in topsoil under different tire load and tire inflation pressure when driving speed was 1 m?s-1

1）由圖11a可知，當W=2.5 kN，p=207 kPa時，垂直應力普遍比其他情況下大；由圖12c可知，當W=1.5 kN，p=69 kPa時，垂直應力普遍比其他情況下小，所以農業耕作中不推薦農業車輛在負載很大的情況下卻使用很大的胎壓。

2）由圖11a和11b可知，當胎壓為207和138 kPa時，輪胎橫向上的垂直應力峰值出現在輪胎中心處；由圖12c可知，當胎壓為69 kPa的時候，輪胎橫向上的垂直應力峰值出現在半寬中心處。

3）由圖 11可知，輪胎前進方向的輪胎前部產生的垂直應力大于輪胎后部產生的垂直應力。

2.4 輪刺對垂直應力分布的影響

當載荷為2.5 kN，胎壓為207 kPa，行駛速度為1 m/s時，輪刺和胎面對應的土壤表層垂直應力如表7。

由表7可得：1）在對應位置，由于輪刺的存在，使得土壤壓實增大，輪刺產生的垂直應力比胎面產生的垂直應力大；2）輪刺產生的垂直應力是胎面產生的垂直應力的1.2～2.3倍，而且越靠近輪胎寬度方向的邊緣，輪刺的影響越大。

在雙因素影響中，利用分形插值的方法模擬出土壤-輪胎接觸面內的垂直應力三維分布狀況，從圖中能夠清晰地看到接觸面內垂直應力的分布規律，得到土壤壓實狀況，以便通過更改影響因素，減小土壤壓實，增加輪胎的通過性；另本文對于輪刺的研究，得出了輪刺和胎面產生的垂直應力的倍數關系。

表7 驅動輪靜止時輪刺對土壤表層垂直應力的影響Table 7 Influence of tire lug of vertical stress in topsoil under static condition of driving wheel

3 結 論

本文著重研究不同載荷、胎壓、行駛速度下，土壤-輪胎接觸面垂直應力的分布情況，并建立了垂直應力和相關因素的預測方程，分析單因素和雙因素對垂直應力分布的影響，主要結論如下：

1）當胎壓為69 kPa時，土壤-輪胎表層垂直應力分布曲線相對平坦，并且垂直應力峰值漸漸出現在距離輪胎邊緣1/4處；而當胎壓為207 kPa時，垂直應力峰值發生在輪胎中心處。這表明：土壤表層垂直應力分布在寬度方向上并不是呈拋物線，而是隨著胎壓的減小，峰值漸漸由輪胎中心處向輪胎邊緣靠近。

2）建立了土壤-輪胎面內垂直應力和載荷、胎壓、行駛速度以及傳感器的位置的預測方程，由預測方程可得：載荷對于垂直應力的影響最大，然后依次是胎壓、行駛速度、縱向距離和橫向距離；垂直應力與胎壓和行駛速度成線性關系，與載荷、橫向距離和縱向距離成拋物線關系。土壤-輪胎面內垂直應力的預測方程基于載荷、胎壓和行駛速度建立的，在實際應用中可改變這些參數，增大輪胎與土壤的接觸面積，使拖拉機有更好的通過性。

3）人字形花紋輪胎中輪刺對于垂直應力的影響很大，輪刺產生的垂直應力是胎面產生的垂直應力的1.2～2.3倍，而且越靠近輪胎寬度方向的邊緣，輪刺的影響越大。