基于LSSVM的反應堆冷卻泵振動趨勢分析
吳茜 呂鑫 王雪梅 鄧志光 徐思捷 朱毖微


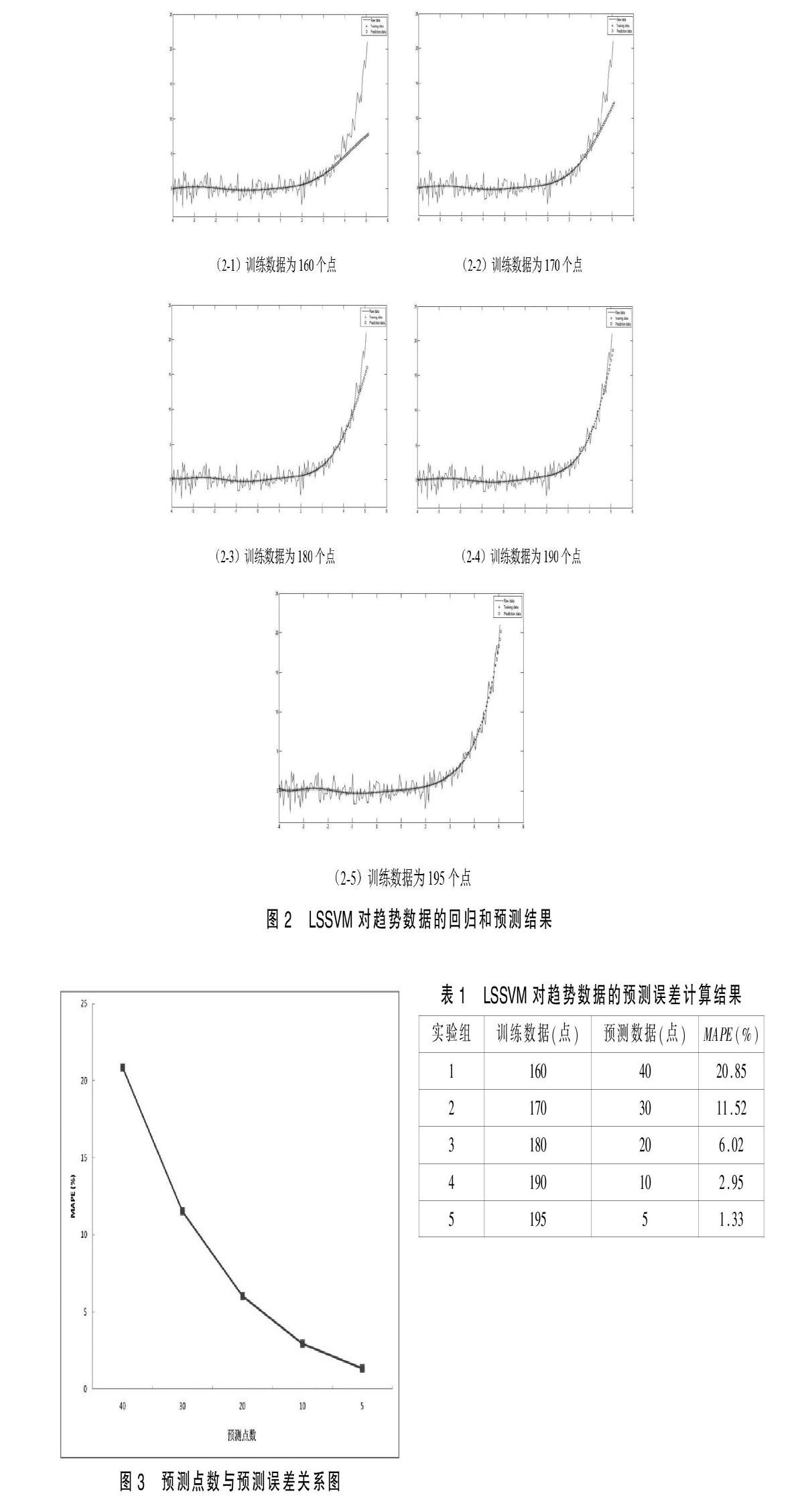
【摘 要】反應堆冷卻劑泵(以下簡稱主泵)作為一回路系統的心臟,其安全性和可靠性至關重要。通過對主泵振動情況進行持續在線監測,不僅能了解主泵運行狀態,更重要的是對振動趨勢的發展進行分析和預測,實現預知維修。針對主泵振動樣本信息不足以及神經網絡等具有代表性的分析預測方法存在的缺陷,本文提出了基于LSSVM的趨勢分析方法。從理論上研究了LSSVM算法對于非線性小容量樣本的優越性,并在算法的基礎上構建了支持向量機回歸預測模型,最后通過仿真數據對其進行了驗證。仿真實驗的結果表明,預測模型表現出較高的精度。因此認為LSSVM算法對主泵振動趨勢具有較好的分析預測能力。
【關鍵詞】LSSVM;趨勢分析;預測模型
中圖分類號: TM623 文獻標識碼: A 文章編號: 2095-2457(2019)11-0067-003
DOI:10.19694/j.cnki.issn2095-2457.2019.11.031
0 引言
反應堆冷卻劑泵(以下簡稱主泵)作為核電站RCS系統的關鍵設備,其工作狀態是否正常直接影響著反應堆的正常運行。為保證主泵的安全可靠運行,不僅要對其進行狀態監測與故障診斷,而且要對其運行狀態的發展趨勢進行預測,實現預防性維護。對主泵振動趨勢的準確分析是預測其運行狀態,實現預防性維護的基礎。目前常見的分析方法為基于神經網絡的方法,但這種方法需要大量的典型數據樣本和先驗知識,由于主泵故障數據獲取困難,增加了建立預測模型的難度。最小二乘支持向量機(Least Squares Support Vector Machine,LSSVM)是一種建立在統計學習理論的VC維理論和結構風險最小化原則基礎上的機器學習方法,其本質是根據有限的信息在模型的復雜性和學習能力之間尋求最優解[1]。它專門針對小樣本數據,具有很強的泛化能力,還能有效克服神經網絡具有的局部極小點、維數災難、過學習等問題。因此,本文將研究運用LSSVM進行核電站主泵振動趨勢分析。
1 主泵振動監測系統簡介
對于大型旋轉機械而言,其振動信號中包含有大量的狀態信息。主泵振動監測系統是通過監測核電站主泵的實際振動響應檢測其性能是否劣化所開發的一種在線監測系統。它能夠提供主泵振動水平和以此為基礎作出的振動趨勢分析,操作人員可據此對主泵運行狀態及其發展趨勢進行評價。
主泵振動監測系統結構如圖1所示,采用振動傳感器和鍵相傳感器分別拾取主泵振動信號和鍵相信號,經過中間處理環節,根據安全分析確定的各種定值,向對應的控制顯示設備發出報警信號。作為主泵振動監測系統的一項重要功能組成,趨勢分析能夠根據采集到的歷史數據對振動特征量的發展趨勢進行分析和預測,估計出主泵振動特征量發展到報警值和危險值的時間。
2 LSSVM算法
LSSVM進行回歸分析的基本思想是升維和線性化。通過一個非線性映射Φ將輸入數據x映射到高維特征空間,在高維空間轉化為線性回歸,從而建立起輸入與輸出之間的函數關系[2]。當有一個新的輸入x∈Rm,通過之前建立的輸入與輸出之間的函數關系就能推導出它所對應的y∈R。用數學語言描述即:對于一個給定的樣本數據{xi,yi},i=1,2,…,n。其中xi∈Rm,yi∈R,xi為輸入,yi為對應的輸出,n表示樣本數據的大小。線性回歸的目標就是求下列回歸函數
式中:ωT∈Rm,b∈R,Φ表示將輸入數據x映射到高維空間的一個非線性映射。
為了解決經驗風險最小化原則下的過學習以及小樣本學習問題,統計學習理論提出結構風險最小化原則,并且在實際問題處理上取得了很好的效果。
結構風險最小化(Structural Risk Minimization,SRM)原則指出,針對實際風險達到最小這一目標,不僅要將經驗風險進行最小化,同時還要考慮縮小置信范圍。對此,統計學習理論提出了一種新的策略,即把函數集構造為一個函數子集序列,使各個子集按照VC維的大小排列,在每個子集中折中考慮經驗風險和置信范圍,取得實際風險最小。
以結構風險最小化原則確定模型參數ω、b,結構風險的計算式為
其中C為正則化參數,Remp為損失函數,又稱為經驗風險。ω的最優解必須要滿足以下兩點:
(1)為了保證回歸函數的平坦以提高其泛化能力,必須尋找到一個ω使得 的值盡量為最小。
(2)ω的值必須使得損失函數的值盡量為最小。
常用的損失函數有一次損失函數、二次損失函數、Hubber損失函數和線性ε不敏感損失函數[3]。不同的損失函數代表不同的支持向量機模型。LSSVM的損失函數為二次損失函數,即
為模型對訓練樣本的預測誤差,則回歸函數的求解問題轉化為了以下優化問題:
建立Lagrange方程求解這個優化問題:
式中:a=[a1,a2,…,an]是Lagrange乘子。
由優化條件
對于非線性問題,根據Vapnik提出的核函數理論[4],可以用核函數K(xi,xj)=<Φ(xj),Φ(xi)>來替代內積運算,實現由低維空間到高維空間的映射,從而使低維空間的非線性問題轉化為高維空間的線性問題。引入核函數后,則
根據樣本數據求解線性方程組可得模型參數[b a1 a2 … an],最終確定回歸函數為
3 基于LSSVM的趨勢分析
3.1 模型的建立
對于特征參量的樣本數據{xi},i=1,2,…,N,取前n個數據作為訓練樣本,后N-n個數據作為測試樣本,對其進行相空間重構,則用于LSSVM學習的訓練樣本為:
m為模型的嵌入維數,則可建立起映射:f:Rm→R。
根據式(11),對訓練樣本可按如下回歸函數進行訓練:

