庫侖阻尼在不同剛度抗沖隔離器中的作用分析

溫肇東，劉洪權*，閆明，張春輝，張磊

1海軍研究院，北京100161

2沈陽工業大學機械工程學院，遼寧沈陽110023

0 引 言

艦船在作戰中，水面非接觸爆炸沖擊載荷會給艦載設備帶來威脅。為保護設備安全運行，主要采取3種方法來抑制沖擊振動，即控制沖擊源頭、改變沖擊傳輸路徑及減小沖擊響應。在實際應用中，最有效的方法是通過抗沖隔振器來減小沖擊響應［1］。在抗沖隔振系統中，剛度和阻尼是2個主要參數。其中，剛度利用自身勢能存儲系統動能以減小被隔離體（設備）的加速度響應，阻尼則是利用能耗性質減小被隔離體的殘余響應并同時增強隔振性的特點，達到減小系統固有頻率在一定帶寬范圍內的沖擊振動響應的目的［2］。

在剛度設計方面，Alabuzhev等［3］基于線性彈簧引入負剛度裝置，對其結構及動態響應進行研究，提出了準零剛度的概念；彭獻等［4］詳細介紹了準零剛度隔振器的定義、分類及其設計方法。除研究準零剛度外，有學者還對主動、半主動剛度開展了研究。例如，Ledezma-Ramirez等［5］介紹了一種開關彈簧裝置，該裝置利用磁力施加恢復力，通過磁力切換剛度的大小。試驗表明，該裝置能減少沖擊響應，弱化殘余振動。

雖然阻尼的機理十分復雜，但是庫侖阻尼作為一種特殊阻尼，其工作原理較為簡單［6］。唐斯密等［7］對半主動干摩擦抗沖隔離器進行了優化設計，通過PID控制方法，確保了隔離器具有良好的隔振性，且使其保持了一定的抗沖擊能力。Ismail［8］對二自由度的庫侖阻尼系統進行了沖擊振動分析，其使用摩擦阻尼控制殘余振動，通過使一個附著在主體上的次級質量塊在摩擦界面上滑動，來達到耗散能量的目的。張萌等［9］采用半波激勵法和速度階躍法分析了庫侖阻尼中粘滯性對沖擊響應的影響，結果表明，該粘滯作用可以減小系統的振蕩，在頻率比較大的系統中，粘滯性是不可忽略的因素。Balandin等［10］對沖擊、振動隔離器進行了優化設計，指出開關彈簧與庫侖阻尼組成的隔離系統可以實現對沖擊的極限保護能力，但并未針對該隔離系統做進一步的分析。

本文將以具有指數規律的運動學方程為依據，分別研究庫侖阻尼下的線性彈簧和開關彈簧系統的沖擊響應，并與粘性阻尼進行對比分析，以探討庫侖阻尼在抗沖隔振系統應用中的優劣性。

1 抗沖隔離系統模型及庫侖阻尼模型

1.1 抗沖隔離系統模型

圖1所示為單自由度的抗沖隔離系統模型。圖中，m為被隔離體（設備）的質量，k為剛度系數，c為阻尼系數，u為在基礎上施加的激勵載荷，y為被隔離體的絕對位移，為基礎的絕對加速度。

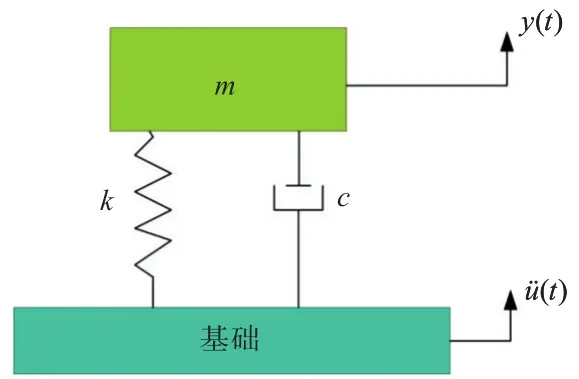
圖1 單自由度抗沖隔離系統模型Fig.1 An isolation system of single-DOF model

令相對位移x=y-u，可得系統的運動方程為

式中：α(c,)sign()為阻尼力；β(k,xn)sign(x)為恢復力；為被隔離體相對速度；為被隔離體相對加速度；為被隔離體相對速度響應；xn為被隔離體相對位移響應；上標r和n均為指數系數。

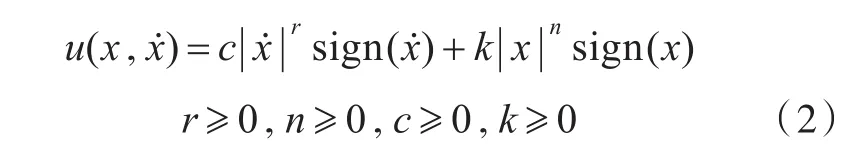
由上式，可以推斷出指數規律特性包含如下6種情況：1）對于項，當 r=0 時，其為庫侖阻尼；2）當r=1時，其為線性阻尼；3）當r=2時，其為平方阻尼；4）對于k|x|nsign(x)項，當n=0時，其大小恒定為開關彈簧彈性力；5）當n=1時，其為線性彈簧彈性力；6）當n≠0且n≠1時，其為非線性彈簧彈性力。

1.2 庫侖阻尼模型

在工程應用中，通常使用sign函數描述庫侖阻尼模型。理想的庫侖阻尼函數為

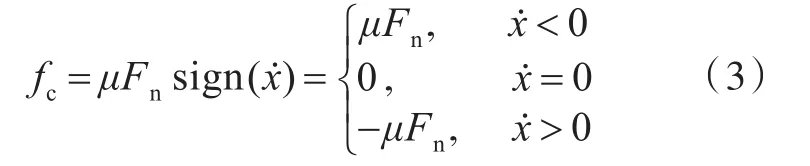
式中：fc為摩擦力（庫侖阻尼力）；μ為摩擦系數；Fn為作用在阻尼系統上的正壓力。

式（3）為理想模型中的阻尼函數，但在工程實際應用中，庫侖阻尼一定會存在粘滯性，若忽略粘滯性，就會使抗沖隔離系統產生振蕩，導致仿真計算結果產生偏差，故在庫侖阻尼計算中應準確描述粘滯性。庫侖阻尼的粘滯性存在于被隔離體由靜止到滑動階段及速度為0的階段。在上述階段，被隔離體所受外力小于μFn，此時的阻尼力應為被隔離體所受外力之和P，故庫侖阻尼模型可重寫為

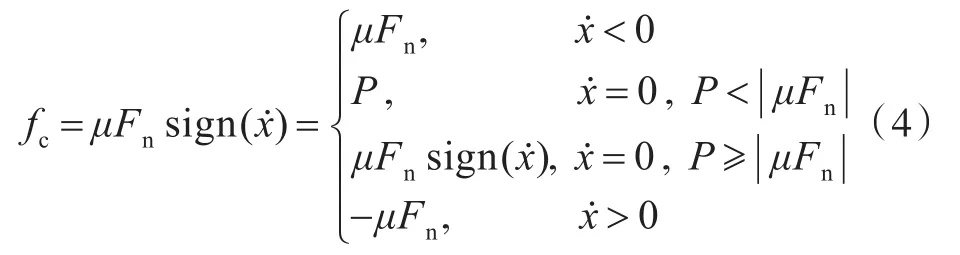
2 線性彈簧—庫侖阻尼抗沖隔離系統

根據模擬的真實海上環境，艦載設備通常會受到來自水面爆炸產生的正、負雙波沖擊。根據德軍標BV 043/85給出的設計沖擊譜（等加速度譜為320g，等速度譜為7 m/s，等位移譜為43 mm），將其轉化為如圖2所示的正、負雙波沖擊下的加速度曲線［11］。本文抗沖隔離系統中，采用的設備質量m=15 kg，系統固有頻率f=10 Hz，該參數在下述各仿真中均保持不變。

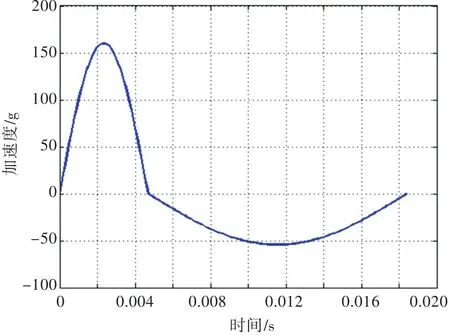
圖2 正、負雙波加速度曲線［11］Fig.2 Curve of acceleration of positive and negative double wave［11］

2.1 線性彈簧—庫侖阻尼系統運動過程分析

本文抗沖隔離系統的阻尼力設定為200 N，計算得到被隔離體的絕對加速度和相對位移曲線如圖3和圖4所示。

圖3 絕對加速度響應曲線Fig.3 Response curve of absolute acceleration

由圖3和圖4可以看出，相對位移曲線比較光滑，且呈衰減趨勢，而絕對加速度則在峰值處產生了跳躍性下降(Δg)，其值恒定為2.72g。出現該跳躍現象的原因是當加速度峰值處的速度為0時，阻尼力的方向發生改變，從而產生了跳躍性變化。

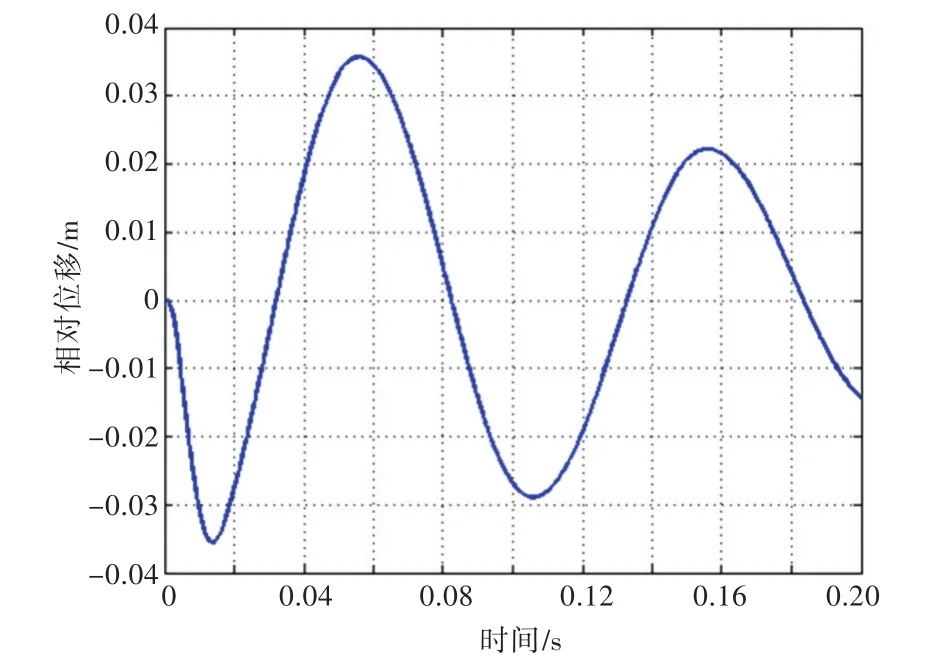
圖4 相對位移響應曲線Fig.4 The response curve of relative displacement

從圖3還可看出，跳躍時間歷程 Δt(Δt=(t+)-(t-))隨著時間的推移而增大，這是阻尼中的粘滯性所致。圖5所示為含粘滯性的庫侖阻尼模型。圖中，為相對速度，為臨界速度。結合圖3與圖5可以看出，隨著時間的推移，被隔離體加速度響應減小，系統在-至的經歷時間變長，故跳躍時間歷程Δt會隨時間的增加而增大。

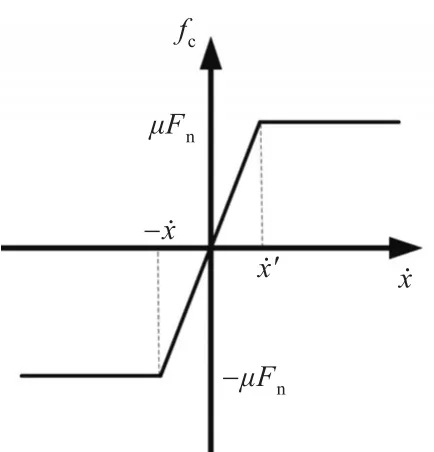
圖5 粘滯性庫侖阻尼示意圖Fig.5 Schematic diagram of viscous Coulomb damping

2.2 線性彈簧—庫侖阻尼系統變化規律

為研究剛度和阻尼對系統的影響，本文將剛度變化倍數k′取為0.1～6倍，庫侖阻尼力fc取為50～300 N，通過仿真計算，得到如圖6～圖9所示的響應曲線。

由圖6～圖8可以看出：系統的絕對加速度幅值隨剛度的增大而增大，在剛度保持不變的情況下，庫侖阻尼力的增加僅使系統的絕對加速度響應幅值稍微降低；相對位移幅值隨剛度的增加先減小后增加，在k′=1的附近產生了局部極小值；相對位移幅值的極小點隨著阻尼力的增加而減小，且極小點處對應的固有頻率隨著阻尼力的增加而增大。

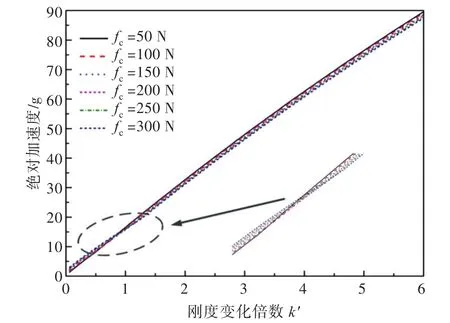
圖6 加速度幅值隨剛度和阻尼力的變化曲線Fig.6 Variation of absolute acceleration amplitude with stiffness and damping

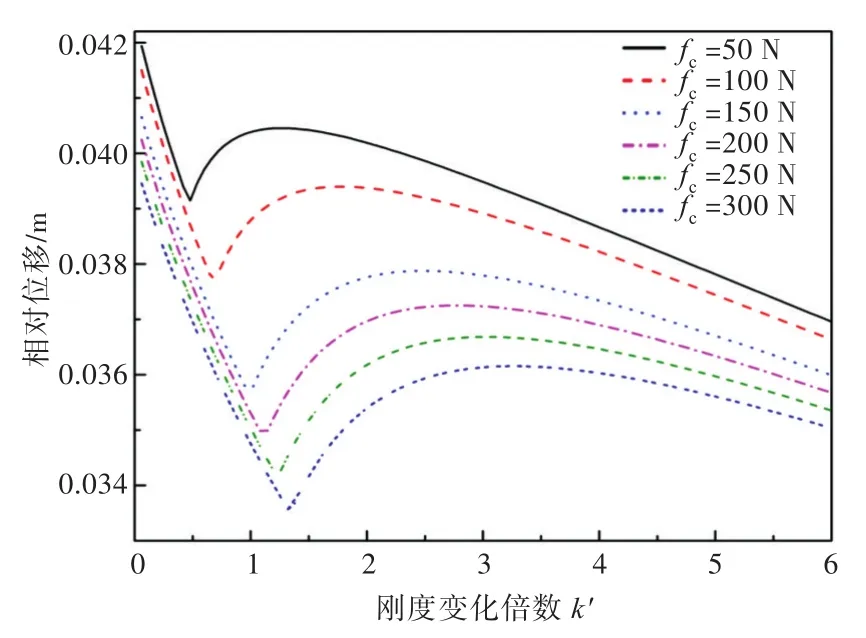
圖7 相對位移幅值隨剛度和阻尼力的變化曲線Fig.7 Variation of relative displacement amplitude with stiffness and damping

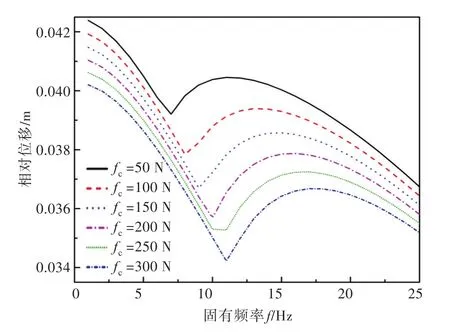
圖8 相對位移幅值隨固有頻率和阻尼力變化曲線Fig.8 Variation of relative displacement amplitude with natural frequency and damping

在研究沖擊響應的過程中，一般將設備絕對加速度響應幅值和相對位移響應幅值的乘積與階躍速度的平方之比稱為系統緩沖系數η，以此表示系統抗沖擊的極限性能，其值越小，說明系統的抗沖性能就越好。圖9給出了不同庫侖阻尼力下系統緩沖系數隨剛度變化的曲線。由圖可以看出，緩沖系數總體上隨剛度的增大而增大，但存在一個轉折點，從而使緩沖系數的斜率變大。

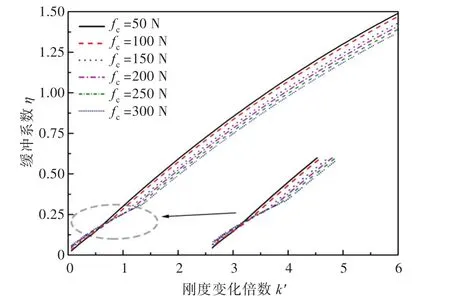
圖9 緩沖系數隨剛度和阻尼力變化曲線Fig.9 Variation of buffer coefficient with stiffness and damping

2.3 線性彈簧—庫侖阻尼系統振動分析

抗沖隔離器除可降低被隔離設備的沖擊響應外，還應具備一定的減振能力。本文對庫侖阻尼系統和粘性阻尼系統進行了對比分析，通過對系統的基礎施加振動信號y(t)=A01sinω01t（其中A01為振動幅值，ω01為固有圓頻率），得到如圖10所示不同庫侖阻尼力下線性彈簧—庫侖阻尼系統相對位移幅頻曲線。

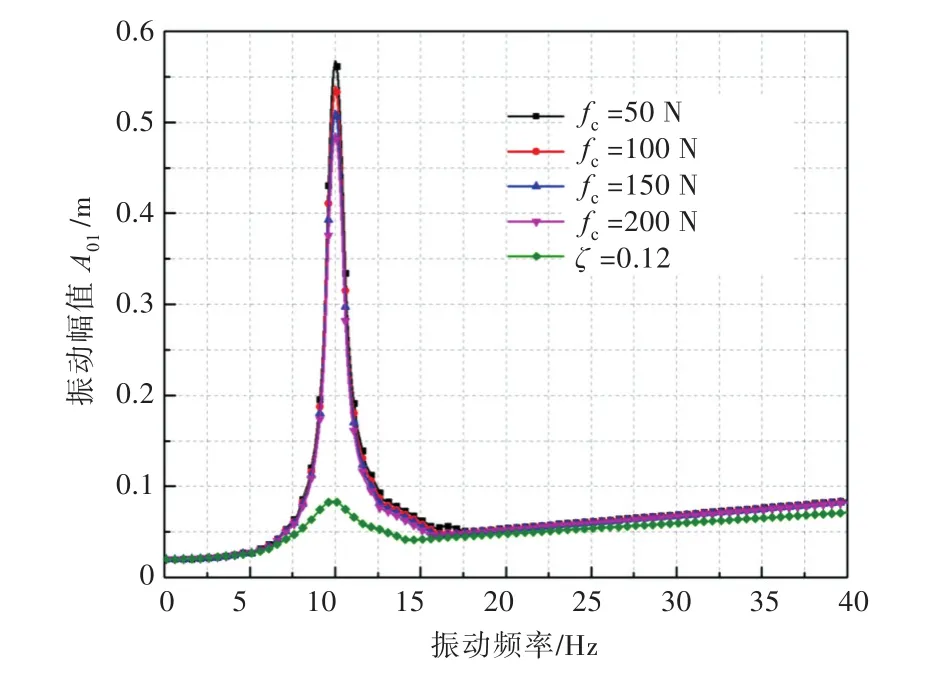
圖10 線性彈簧—庫侖阻尼系統相對位移幅頻曲線Fig.10 Response curves of relative displacement amplitude for linear spring-Coulomb damping system

由圖10可以看出，庫侖阻尼在線性彈簧中可以減小系統固有頻率附近（5 Hz＜f＜15 Hz）的共振幅值，每增加50 N的阻尼力，可降低0.02 mm的振動幅值。根據庫侖阻尼與粘性阻尼等效的原則，對比分析了庫侖阻尼力為100 N的粘性阻尼（等效阻尼比ζ=0.12）的振動特性。結果發現，摩擦阻尼力的減振效果遠不如粘性阻尼，粘性阻尼相比于庫侖阻尼可減小84.7%的位移幅值。

3 開關彈簧—庫侖阻尼抗沖隔離系統

開關彈簧也是一種恒力緩沖裝置，圖11所示為文獻［12］設計的一種恒力緩沖裝置。為避免被隔離體與恒力緩沖裝置間出現剛性碰撞，在緩沖裝置凸輪滑軌的支撐頭上設計安裝了一個橡膠墊，以起到過渡的作用。該橡膠墊的等效線性剛度記為keq。

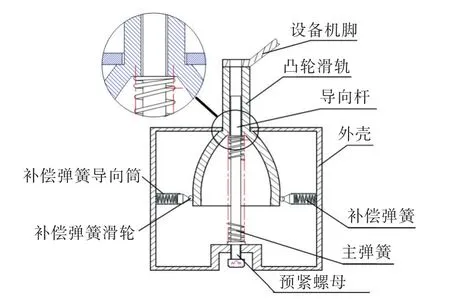
圖11 恒力緩沖裝置示意圖Fig.11 Schematic diagram of constant force buffering device

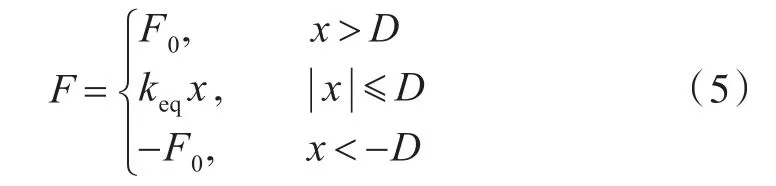
鑒于開關彈簧與庫侖阻尼相似，開關彈簧的彈性力F與位移的函數關系可以表示為式中：F0為恒力緩沖裝置力；keq為彈簧緩沖元件的等效線性剛度；D為彈簧中緩沖元件的控制范圍。根據式（1），可推導出該模型的運動方程為

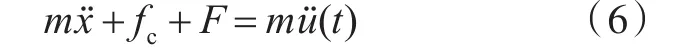
3.1 開關彈簧—庫侖阻尼系統運動過程分析

本文在分析開關彈簧—庫侖阻尼系統的運動過程時，將開關彈簧的彈性力設為1 500 N，阻尼力設為200 N，被隔離體質量設為10 kg，計算得到如圖12和圖13所示的響應曲線。

由圖12可以看出，在開關彈簧—庫侖阻尼系統中，絕對加速度的跳躍現象非常明顯，系統中由開關彈簧引起的跳躍為 Δg1(Δg1=2*F0/9.8*m)，在受到沖擊的瞬間，被隔離體的絕對加速度達到峰值，此現象是由開關彈簧的彈性力所致。由于開關彈簧中緩沖元件的控制范圍D很小，被隔離體的相對位移迅速超過D，使彈性力達到峰值，從而使絕對加速度也達到峰值。其后，被隔離體在位移峰值、速度為0處產生了較小的向下跳躍Δg2。

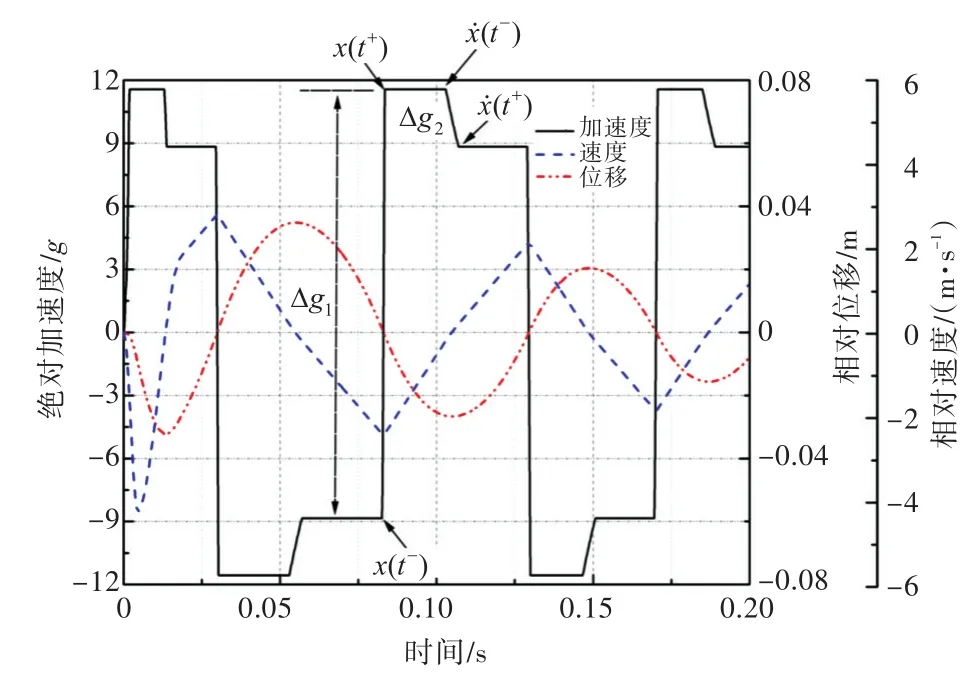
圖12 絕對加速度、相對速度、相對位移響應曲線Fig.12 Response curves of absolute acceleration，relative velocity and relative displacement

圖13 阻尼力與彈性力響應曲線Fig.13 The response domain curves of damping force and elastic force

3.2 開關彈簧—庫侖阻尼系統變化規律

為對開關彈簧—庫侖阻尼系統進行分析，將開關彈簧的彈性力取為1 000～5 000 N，阻尼力取為100～500 N,被隔離設備質量取為15 kg，計算得到如圖14～圖16所示的變化曲線。

由圖14和圖15可以看出，絕對加速度幅值隨開關彈簧彈性力和阻尼力的增大呈線性增加；相對位移幅值隨開關彈簧彈性力的增加呈先減小后增大的趨勢，即每個阻尼都存在一個特定的彈性力（恒力）使其相對位移值最小，同時該最小值對應的彈性力隨阻尼力的增大而增大。

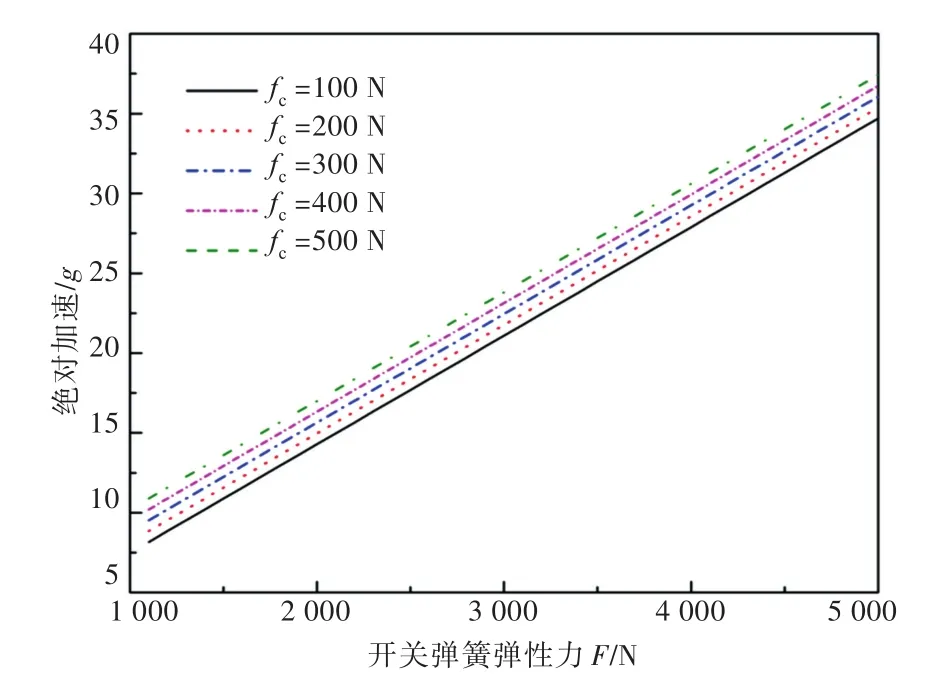
圖14 絕對加速度幅值隨開關彈簧彈性力變化曲線Fig.14 Variation of absolute acceleration amplitude with elastic force of switch spring

由圖16可以看出，系統緩沖系數總體上隨開關彈簧彈性力和阻尼力的增大而呈線性增加，但在相對位移中存在最小值點，緩沖系數會產生一個轉折點（見圖中箭頭處）。在轉折點前，緩沖系數隨開關彈簧彈性力的增加而增加較為平緩，過了轉折點后，緩沖系數增加的斜率較大，并一直保持不變。

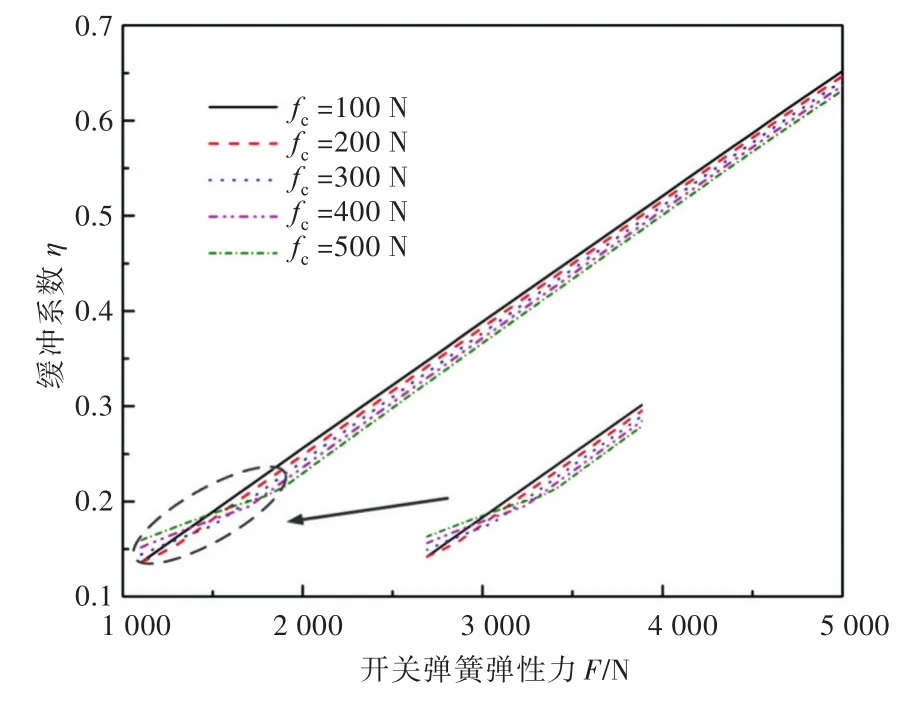
圖16 緩沖系數隨開關彈簧彈性力變化曲線Fig.16 Variation of buffer coefficient with elastic force of switch spring

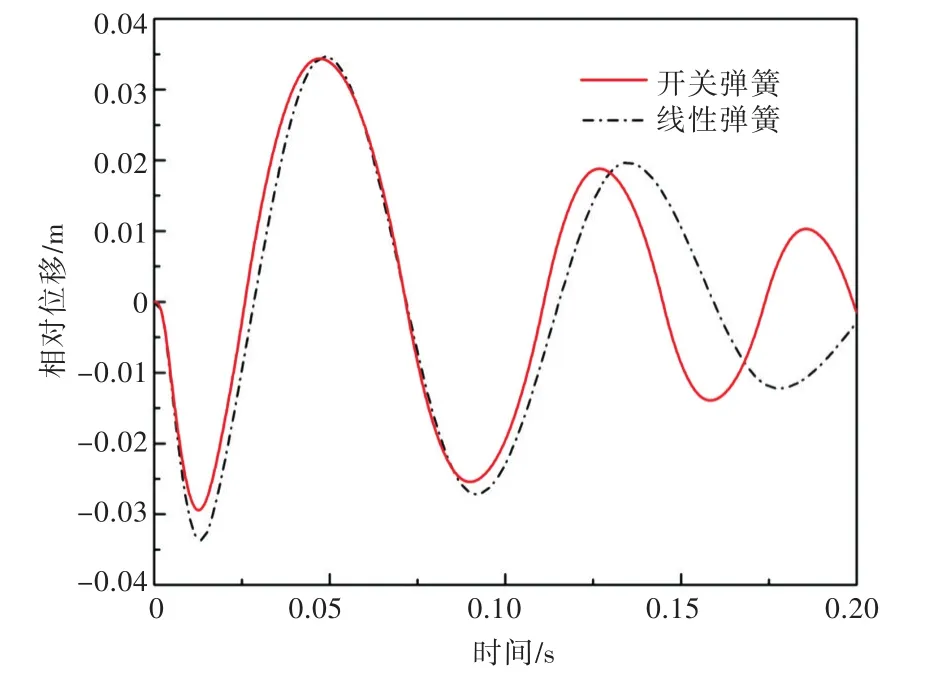
圖17 開關彈簧與線性彈簧的相對位移響應曲線Fig.17 Response curves of relative displacement for switch spring and linear spring

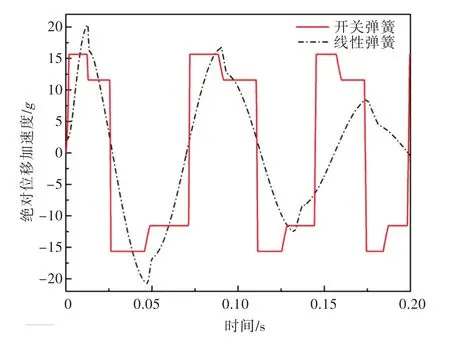
圖18 開關彈簧與線性彈簧的絕對位移加速度響應曲線Fig.18 Response curves of absolute acceleration for switch spring and linear spring

4 開關彈簧與線性彈簧、庫侖阻尼與粘性阻尼對比分析

4.1 開關彈簧與線性彈簧的對比分析

為分析開關彈簧與線性彈簧在庫侖阻尼系統中的響應特點，在相同的沖擊環境下，并保證阻尼力與最大相對位移幅值相同，對比了上述2種彈性系統的相對位移與絕對位移加速度響應，如圖17和圖18所示。

由圖17和圖18可以看出，開關彈簧—庫侖阻尼系統的絕對位移加速度響應峰值要小于線性彈簧—庫侖阻尼系統，但由于開關彈簧與庫侖阻尼均為恒力，故在時域中絕對位移加速度未衰減；經過一個半周期后，線性彈簧—庫侖阻尼系統的絕對位移加速度響應幅值開始小于開關彈簧系統。

4.2 庫侖阻尼與粘性阻尼的對比分析

為分析庫侖阻尼與粘性阻尼在開關彈簧中的沖擊響應特點，在相同的沖擊環境下，并保證開關彈簧恒力大小一致，同時庫侖阻尼系統與粘性阻尼（線性阻尼）系統的最大相對位移幅值也相同，對比了上述2種阻尼系統的相對位移與絕對加速度響應，如圖19和圖20所示。

圖19 粘性阻尼與庫侖阻尼相對位移響應曲線Fig.19 Response curves of relative displacement for viscous damping and Coulomb damping

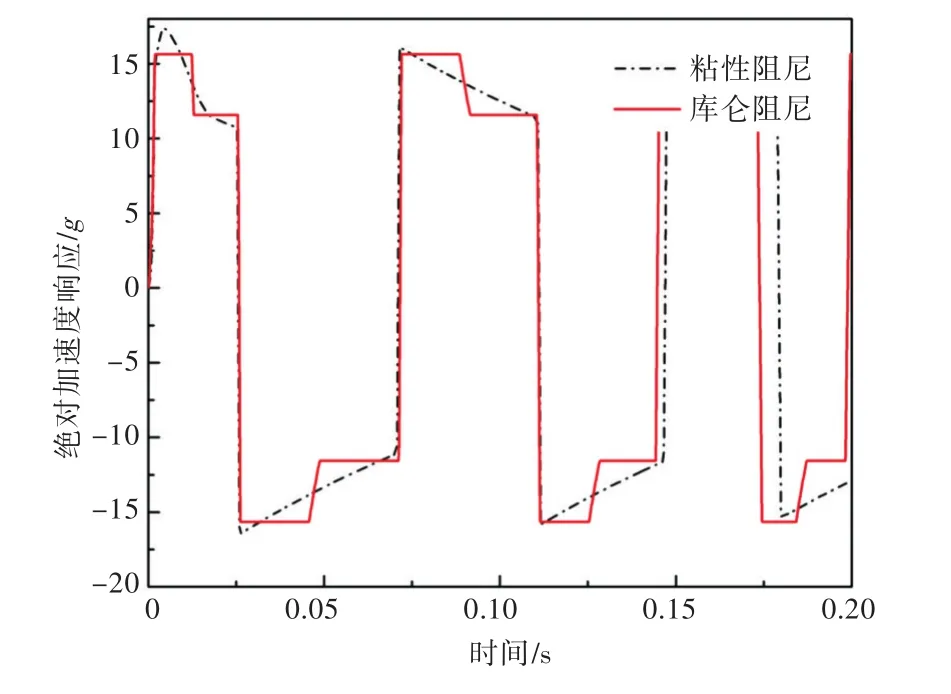
圖20 粘性阻尼與庫侖阻尼絕對加速度響應曲線Fig.20 Response curves of absolute acceleration for viscous damping and Coulomb damping

由圖19和圖20可以看出，在第1個周期內，庫侖阻尼系統的絕對加速度幅值略小于粘性阻尼系統；隨后，粘性阻尼系統的絕對加速度響應幅值與庫侖阻尼系統的響應幅值接近于相等，而庫侖阻尼與粘性阻尼系統的相對位移幅值在第1個周期結束后開始出現差別，亦即庫侖阻尼系統的相對位移幅值逐漸小于粘性阻尼系統。可見，庫侖阻尼系統的性能要優于粘性阻尼系統。

5 結 論

本文通過對庫侖阻尼在不同剛度下并聯組成的抗沖隔離系統的作用進行分析，得到如下結論：

1）在線性彈簧—庫侖阻尼系統中，相對位移響應幅值隨剛度變化倍數（1＜k′＜1.5）和固有頻率（7 Hz＜f＜12 Hz）的變化，存在一個極小值點，當剛度變化倍數k′＞3、固有頻率f＞15 Hz時，位移響應幅值逐漸減小；該系統中阻尼力對隔沖性的影響較小，剛度越小的系統其絕對加速度響應幅值越小，但當剛度很小時，系統的恢復力就很小，甚至不能使系統恢復到原位。

2）在開關彈簧—庫侖阻尼系統中，相對位移響應幅值隨彈簧彈性力F的增加呈先減小后增大的趨勢，并在1 000 N＜F＜1 500 N范圍內存在最小值；阻尼力的增加會增大絕對加速度響應，但可降低相對位移幅值。

3）開關彈簧—庫侖阻尼系統無論是在抑制絕對加速度響應幅值方面，還是在降低殘余響應方面，均略優于開關彈簧—粘性阻尼系統。