基于反饋粒子濾波的船舶模型參數辨識

鄭涵，俞孟蕻，袁偉

江蘇科技大學電子信息學院，江蘇鎮江212003

0 引言

目前，許多工程船都安裝了動力定位系統。動力定位系統主要用于在不借助錨泊系統的情況下，通過控制器的計算使船舶依靠自身推進系統抵抗風、浪、流等環境的影響，以保持在某目標位置或者按照一定的軌跡航行，從而完成各種作業功能。動力定位系統的主要目的是實現船舶縱蕩、橫蕩和艏搖3個自由度的控制，其優點是不受水深的限制，定位精確，機動性強。若要在動力定位系統中建立船舶運動模型，就需確定模型中的參數值［1］。近年來，系統辨識理論的快速發展為船舶運動模型的建立提供了新的思路和方法。Fossen等［2］采用的擴展卡爾曼濾波方法已被廣泛用于船舶運動模型參數的辨識中。隨后，邊信黔等［3］提出了動力定位控制系統模型參數的離線最速下降尋優辨識方法，采用該方法不僅節約了辨識時間，減少了試驗費用，而且還提高了動力定位系統的工作效率。邢家偉［4］采用遺忘因子最小二乘法與自適應遺傳算法相結合的參數辨識方法，對船舶運動數學模型中的慣性矩陣和線性水動力阻尼矩陣進行了辨識，證明該方法對其矩陣的辨識有效、可行。李春風等［5］利用免疫遺傳神經網絡對艦船水動力系數進行了辨識。丁彥侃［6］提出了一種改進的并行擴展卡爾曼濾波算法，用來辨識船舶運動模型參數。由于非線性誤差積累等方面的問題，參數辨識的效果往往不好。本文將根據動力定位系統設計的需要，提出一種辨識效果更好的反饋粒子濾波算法［7-12］來辨識模型中的參數，通過辨識實驗，仿真驗證該方法的有效性和可靠性。

1 船舶數學模型

船舶動力定位系統主要控制船舶在水平面的3個自由度的運動，分別為縱蕩、橫蕩和艏搖。為了描述船舶的水平面運動，建立了如圖1所示的坐標系。首先，建立大地（Earth-Centered，Earth-Fixed，ECEF）坐標系 XOY；其次，在船體上建立船體坐標系xoy，坐標平面xoy在水平面內，原點o位于船舶重心處，ox軸指向船艏，oy軸指向船舶右舷正橫方向。

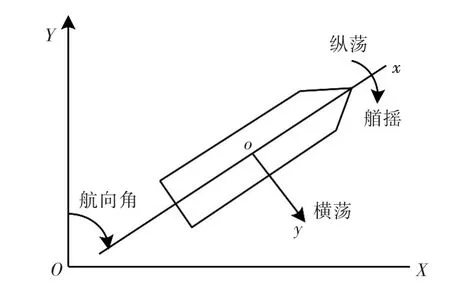
圖1 兩種坐標系的定義Fig.1 The definition of ECEF coordinate system and body coordinate system

以船的重心為參考點，根據船舶操縱性理論和動力定位系統的特征，建立船舶數學模型［13］：

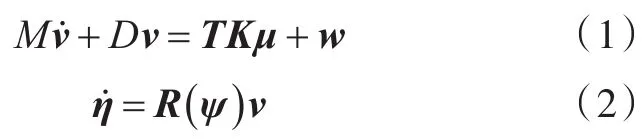
式中：TKμ為推進器、舵的控制力和力矩矢量，其中T為實船控制配置矩陣，μ為由實船操縱中給出的控制命令，K為待辨識的推進器系數矩陣；w為由風、浪、流等作用力組成的環境干擾力；，包括大地坐標下的位置和艏搖角度ψ；，包括船舶在隨船坐標系下的縱蕩速度u、橫蕩速度υ和艏搖角速度r；R(ψ)為大地坐標系和隨船坐標系的轉換矩陣，

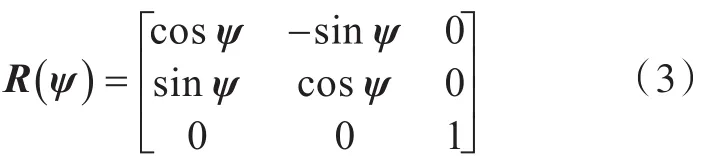
M，D分別為質量矩陣和阻尼參數矩陣，

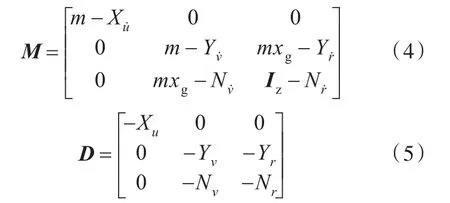
式中：m為船舶質量；Iz為隨船坐標系xoy的轉動慣量；xg為船舶質心到隨船坐標原點的距離，將隨船坐標系的原點取在船舶重心上，則為船舶在各個運動方向上的附加質量系數，可以通過理論估算［14］得出；Xu，Yv，Yr，Nv，Nr為船舶在各個運動方向上的水動力阻尼系數，線性水動力阻尼矩陣D為需要辨識的未知量。

2 反饋粒子濾波算法

由于擴展卡爾曼濾波的非線性誤差積累問題，參數辨識的精度往往不高［15］。本文將采用一種免重采樣非線性濾波算法——反饋粒子濾波（Feedback Particle Filter，FPF）算法來避免該問題。FPF算法是將每個粒子作為一個可控的隨機系統，通過求解歐拉—拉格朗日邊界值問題，得到在Kullback-Leibler距離最小意義下的最優反饋控制律，然后再根據前一時刻對粒子自身的狀態進行校正和更新。不同于粒子濾波，反饋粒子濾波算法不需要重采樣步驟，可以有效避免因估計狀態維數增加而導致的計算量增大［15］問題，易于實際工程應用。

假設連續時間動態系統的狀態方程和觀測方程如下：

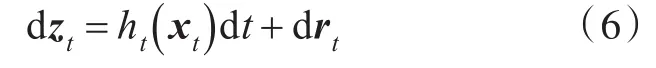
式中：xt為系統狀態向量，xt∈Rd，其中d為系統的狀態維數；zt為觀測向量；zt∈Rm，其中m為系統的觀測維數；ft(·)為系統狀態方程；ht(·)為觀測方程；wt和rt分別為系統過程噪聲和觀測噪聲。對連續時間系統采用歐拉法進行離散化處理，粒子的離散化方程為

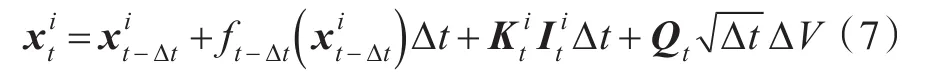
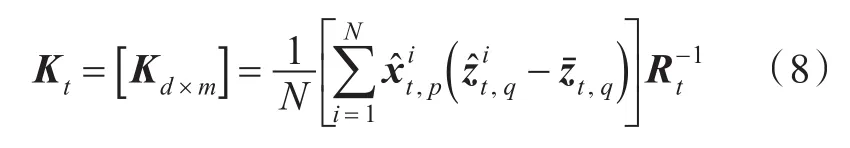
式中：Kt為一個d×m維的矩陣；p=1,2,3,…,d；q=1,2,3,…,m；分別為系統的狀態預測向量和觀測預測向量：

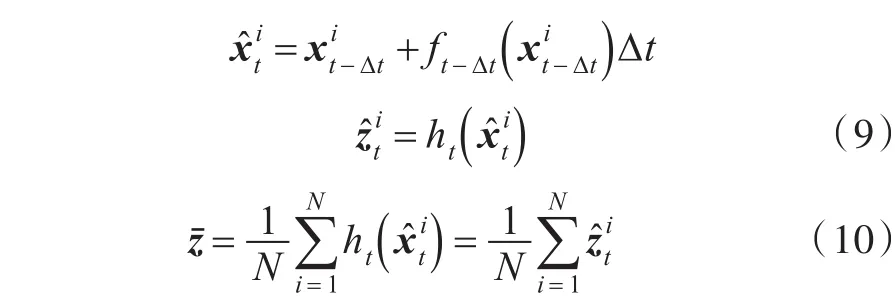
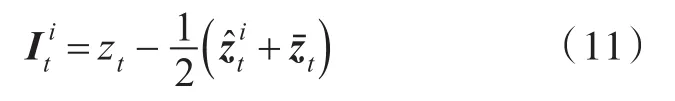
由以上FPF的算法公式可以看出，FPF基于誤差更新的反饋增益控制結構仍然存在，其與線性卡爾曼濾波（Linear Kalman Filter，LKF）的反饋增益結構對比如圖2所示。

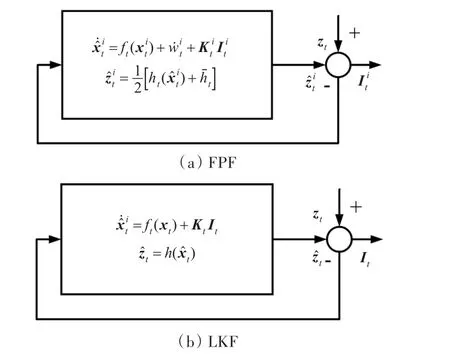
圖2 反饋增益結構比較Fig.2 Comparison of feedback gain structure

3 運動模型參數辨識

為便于進行實驗，將式（1）、式（2）中的船舶運動數學模型解耦，分離出縱蕩運動數學模型以及橫蕩與艏搖運動數學模型。船舶在僅主推進器工作的情況下采用縱蕩運動數學模型，在僅側推進器工作的情況下采用橫蕩與艏搖運動數學模型。分別對這2個模型進行參數辨識海上實驗，記錄船舶在這2種狀態下的實驗數據。利用數學模型和實驗數據，在Matlab平臺上編寫FPF算法程序，進行仿真實驗。

3.1 縱蕩參數辨識

船舶只使用主推進器，使船舶縱向前進，辨識縱蕩阻尼參數Xu和2個主推進器系數k1，k2。

由船舶運動數學模型分離出的縱蕩運動模型，得到狀態方程和觀測方程為

式中：u為狀態變量；μ1為輸入變量；z1為輸出變量；w1，r1分別為縱蕩運動模型中的過程噪聲和觀測噪聲；Xu與K1為需要辨識的參數。

3.2 橫蕩與艏搖參數辨識

船舶只使用側推進器，使船舶橫向前進并產生艏搖角度，辨識橫蕩與艏搖阻尼系數Yv，Yr，Nv，Nr和側推進器系數k3。

由于橫蕩與艏搖運動的速度項和加速度項的系數有耦合，為便于求解，引入了一個動量h，定義h=Mv。從船舶運動數學模型中分離出橫蕩與艏搖運動模型，得到狀態方程和觀測方程為

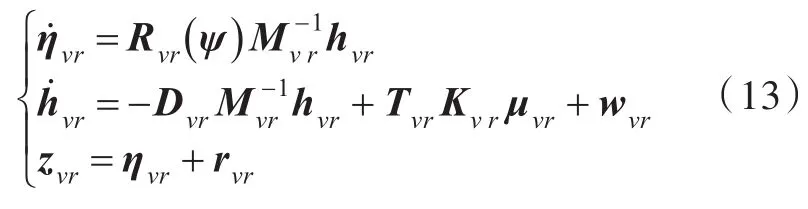
其中，

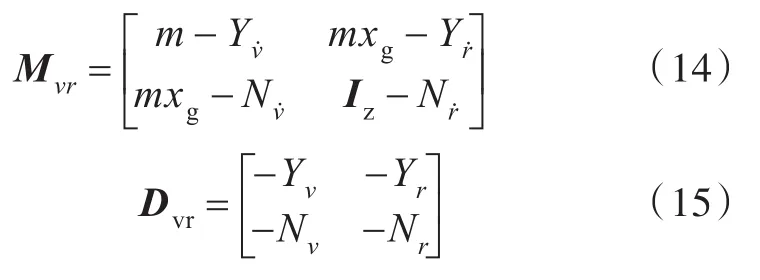
式中：hvr為狀態變量；μvr為輸入變量；zvr為輸出變量；wvr，rvr分別為橫蕩與艏搖運動模型中的過程噪聲和觀測噪聲；矩陣Dvr與Kvr為需要辨識的參數。

4 實驗及分析

4.1 研究對象

本實驗數據由一艘大型自航耙吸挖泥船“新海虎9”號于海上實驗中獲得。該船總長128 m，型寬25.6 m，型深9.2 m，設計吃水6.8 m，總載重量13 710 t，滿載航速15 kn。推進系統由2個主推進器和1個側推進器組成。選取合適的實船數據600組，得到船舶在固定坐標系的位置(X,Y)，船的艏搖角度ψ，船舶航速ν，左、右兩側主推進器推力μ11和μ12，以及側推進器推力μvr。設置采樣間隔時間Δt=0.1 s，粒子數N=500，過程噪聲方差Q=0.1Id×d，觀測噪聲方差R=0.01Im×m。

4.2 參數辨識實驗

采用FPF算法分別進行縱蕩辨識實驗及橫蕩與艏搖辨識實驗，辨識結果如表1所示。

表1 參數辨識結果Table 1 Parameter identification results

4.3 仿真結果驗證

分別采用FPF和擴展卡爾曼濾波（Extended Kalman Filter，EKF）這2種算法對推進器系數k1，k2，k3進行辨識，辨識結果如圖3所示。

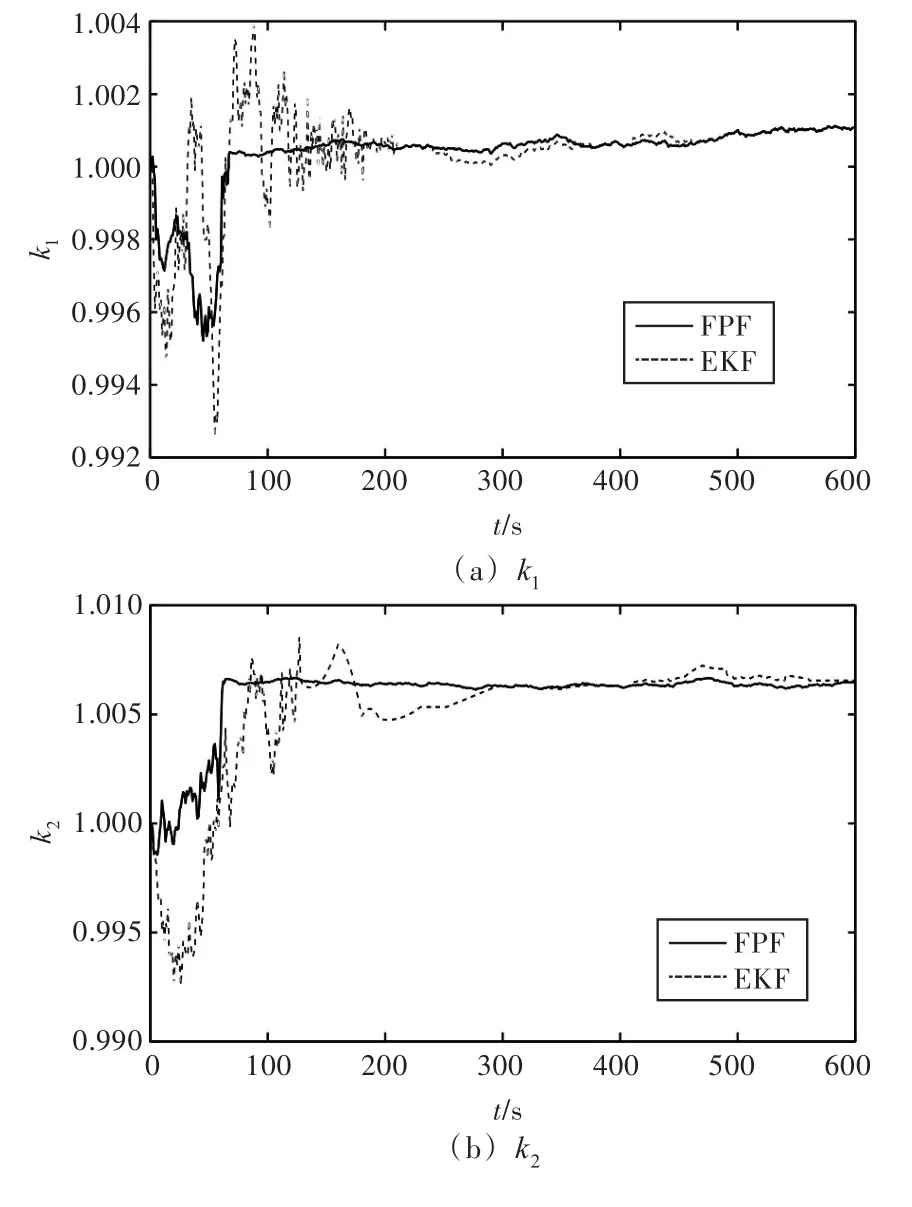
圖3（a）和圖3（b）中的k1，k2由縱蕩模型實驗得出，圖3（c）中的k3由橫蕩與艏搖模型實驗得出。由圖3可以看出，FPF算法的振蕩幅度較EKF算法小很多，在遞推100次左右趨于平穩，而EKF算法則在遞推200次左右才趨于穩定，且圖3（b）中顯示，EKF算法在趨于穩定之后仍然存在明顯的波動。可見，FPF算法的收斂速度更快，穩定性更好。

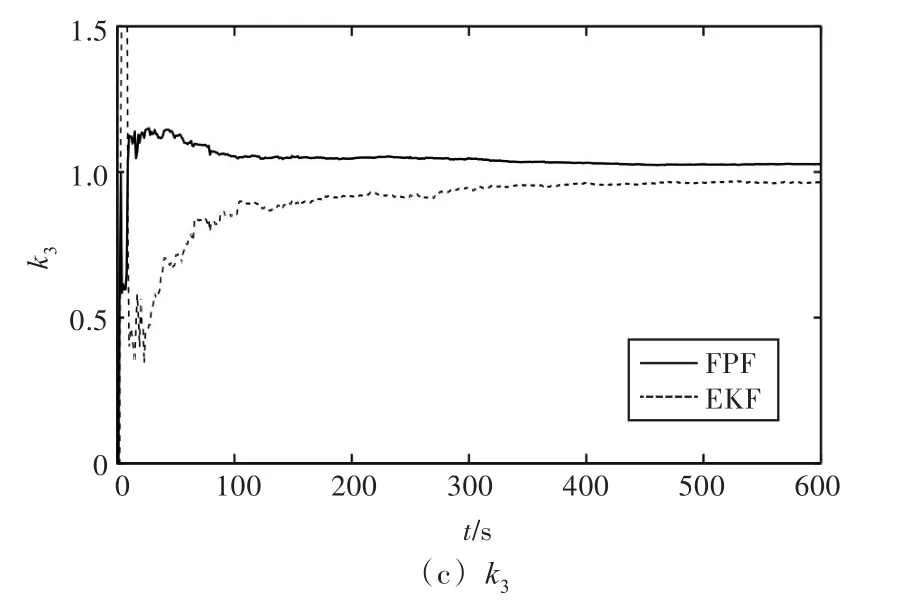
圖3 參數值k1，k2，k3的仿真結果對比Fig.3 Comparison of simulation results ofk1，k2，k3

4.4 模型可靠性分析

通過對模型參數的估計，建立船舶運動數學模型，用模型進行運動仿真。由于實驗結果的數值較大，將仿真值與實測數據進行對比不易于觀察，因此，繪制了如圖4所示的二者的差值仿真圖。在縱蕩實驗中得到船舶運動距離和航速的仿真值，然后與實測數據進行對比得到距離差值和航速差值；在橫蕩與艏搖實驗中得到船舶運動距離和艏向角的仿真值，然后與實測數據進行對比得到距離差值和艏向角差值。

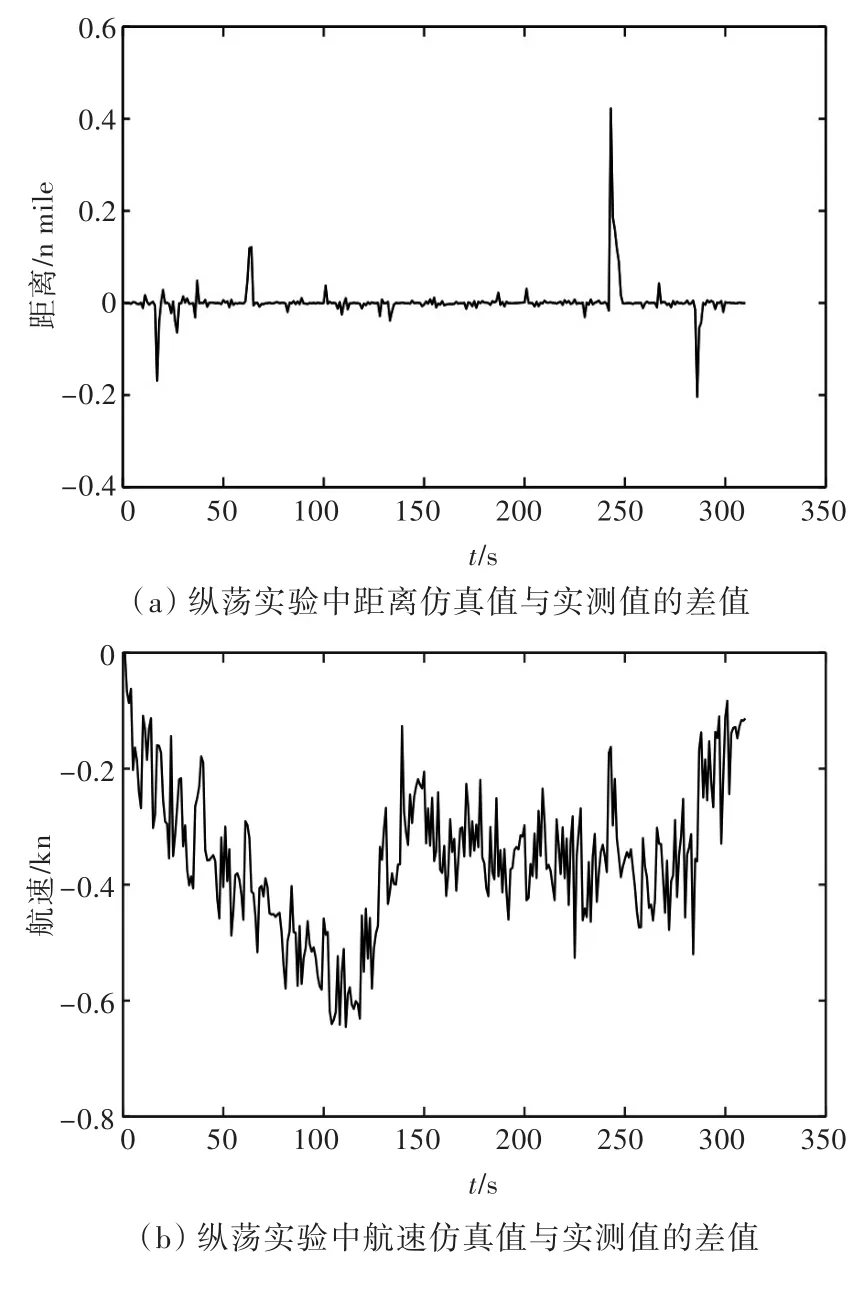
仿真結果表明，在采用FPF參數辨識方法建立的船舶運動模型中，仿真值與實測值之間的差值穩定在較小范圍內，具有可靠性。圖4（a）中，由于在實驗數據記錄等過程中產生的誤差峰值點數量較少，故忽略不計。

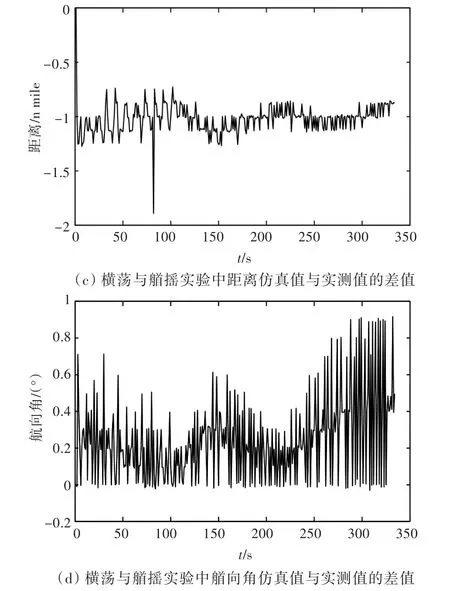
圖4 仿真值與實測值的差值圖Fig.4 Differential chart between simulated values and measured values

5 結 語

本文針對傳統擴展卡爾曼濾波方法的不足，提出了一種新型的FPF算法并應用到了船舶運動數學模型的參數辨識中。分離船舶運動模型，建立縱蕩運動模型及橫蕩與艏搖運動模型并分別進行辨識實驗。通過Matlab仿真，得到運動模型里待辨識的推進器推力系數，發現辨識的收斂速度更快，穩定性更好，證明了該算法的有效性。實驗結果表明，本文所提出的FPF算法能夠較好地應用到船舶運動數學模型的參數辨識中，可使其辨識效果與真實值更接近。該算法可靠，能夠滿足船舶模型參數辨識的需要。