CoreXY機構3D打印機運動控制算法研究

（河北工業大學 機械工程學院 機械工程系，天津 300130）

0 引言

近年來3D打印機、激光雕刻機、激光切割機以及激光打標機等智能設備興起，引發了科技愛好者的興趣。CoreXY機構是廣泛應用于這些設備中的機構之一，CoreXY結構相對緊湊，同樣體積的情況下，可以實現相對較大的打印尺寸；對于CoreXY結構，在XY平面內運動的兩個電機都固定，降低了運動部件的重量，這樣也就降低了運動部件的慣性，同樣驅動力的情況下，加速度更高，帶來的效果就是運動更加敏捷。相對于笛卡爾直角坐標機構、Delta機構[1]，CoreXY機構具有明顯的優勢。為了更加高效精確的控制它，目前比較流行的是廣泛用于數控機床控制的插補算法，常用的插補算法有逐點比較法、最小偏差法、Bresenham直線生成算法（計算機圖形學中繪制直線的一種經典算法[2]）等。這些算法的優點是算法簡單、插補計算速度快、插補誤差較小，但同時也存在如下缺點：1）不能兩軸聯動，影響加工精度；2）插補次數多，執行時間長，影響生產效率[3]。所以為了提高機構的執行效率和加工精度，引入一種高精度高效率的算法尤為重要。

熔融沉積成型（Fused Deposition Modeling，FDM）是將絲狀的熱熔性材料加熱融化，同時三維擠出機構在計算機的控制下，根據截面輪廓信息，將材料選擇性地涂敷在工作臺上，快速冷卻后形成一層截面。一層成型完成后，機器工作臺下降一個高度（即分層厚度）再成型下一層，直至形成整個實體造型[4]。對于CoreXY 結構的FDM型3D打印機來說，為了快速的打印出高精度的產品模型，需要對打印機的X軸、Y軸、Z軸以及E軸（擠出機構）的聯動控制，四者密切配合運動、缺一不可。尤其是X、Y平面的運動對一臺3D打印機的打印質量尤為重要；因此實現對平面機構的控制成為3D打印的核心。本文著重論述CoreXY平面機構的運動控制，Z軸和E軸的運動控制相對較為簡單，不再詳細論述。目前一些主流的3D打印機固件不開源、國內外相關研究資料較少，算法改進與移植困難，這給我們的研究帶來困難。本文將數控技術應用于3D打印行業，這將會大大方便3D打印愛好者的開發，同時也降低了入門難度。CoreXY結構3D打印機由于其獨特的傳動方式，以及其較其他機構的鮮明優勢，這種機構的應用前景將不可限量。

為了更準確高效地實現對CoreXY機構的運動控制，本文對CoreXY結構所獨有的X、Y平面機構進行運動特性分析，將該機構與典型的直角坐標機構建立一定的數學轉化關系，引入了一種比最小偏差法更優的算法。

1 機構特點與運動分析

CoreXY機構最大特點是步進電機都固定在機架一側，無論運動機構沿X軸還是沿Y軸向運動，兩個步進電機都不會隨著機構運動，因此減輕了機器在運動過程中的負擔，使運動機構的動作更加平穩。CoreXY機構的原理圖如圖1所示。整個機構的各種運動方式都是通過一根皮帶的傳動來實現的，這種傳動方式可以有效減輕振動，且避免了安裝絲杠、移動步進電機的負擔，使整體結構更加簡單，運動更加靈活，能夠在一定程度上提高機構的工作效率。

機構運動位移ΔX，ΔY與步進電機M1、M2的線位移ΔA、ΔB之間的關系如式(1)和(2)所示：

解方程組可得：

上式中：ΔX、ΔY 分別為3D打印機工料擠出機構所在的滑塊分別沿X正方向和沿Y正方向的位移，ΔA、ΔB分別為步進電機M1、M2的線位移，為了方便以順時針為負、逆時針為正來標記ΔA、ΔB的方向。

圖1 CoreXY 機構傳動原理示意圖

當步進電機M1和M2以相同的速度順時針或逆時針同向轉動時，機構的滑塊就會沿X軸方向水平運動，ΔA、ΔB的大小、方向相同；此時有：

當步進電機M1和M2以相同的速度、相反的方向轉動時，機構的滑塊就會沿Y軸方向運動，此時：ΔA、ΔB的大小相同，方向相反；此時：

當步進電機M1轉動，步進電機M2靜止時，滑塊將沿著Y=X方向移動；此時：

同理當步進電機M2轉動，步進電機M1靜止時，滑塊將沿著Y=-X方向移動；此時：

由上可知，CoreXY機構可以非常方便的實現滑塊沿著X、Y軸方向和Y=X、Y=-X方向移動，這就為下文的控制算法引入埋下伏筆。

2 運動控制算法研究

2.1 逐點比較法

這里我們先引入逐點比較法，逐點比較法的廣泛應用于數控領域，近來隨著增材制造和激光加工的興起，該算法也被應用于FDM型3D打印機的控制中。

要實現3D打印機的連續運動，需要將建立好的三維模型用切片軟件進行切片，得到所需打印模型的G代碼，代碼中存放的是無數層切片的坐標值，要重復這些軌跡，就要實現擠出機構從當前點C（X0，Y0）到目標點D（X1，Y1）的插補運動[5]。

逐點比較法插補過程的每一步都要經過以下四個工作節拍。

1）坐標判斷：計算擠出機構的當前位置C（X0，Y0）與目標位置D（X1，Y1）的差值Xe，Ye，并根據Xe，Ye的符號，判斷進給方向。

2）坐標進給：根據當前偏差Fn判別的結果，控制機構沿相應的坐標軸進給一步，使擠出機構向模型輪廓靠攏。

3）偏差計算：擠出機構進給一步后，針對新的擠出機構位置，計算新的偏差值Fn+1。

4）終點判別：擠出機構進給一步后，需要判別擠出機構是否已經到達零件輪廓的終點。如果已經到達終點，則停止插補過程，目標位置賦值為當前位置；如果未到達終點，則返回到第1）步，重復上述四個節拍[6]。表1為打印機擠出機構各卦限的運動判斷公式。

表1 逐點比較法插補公式表

擠出機構在具體卦限的具體進給方向和偏差判斷如圖2，偏差F≥0時，擠出機構沿著X軸運動，F＜0時擠出機構沿著Y軸運動，步進電機M1和M2以相同的速度順時針或逆時針同向轉動時，就可以沿著X軸運動，步進電機M1和M2以相同的速度順時針或逆時針反向轉動時，就可以沿著Y軸運動。不妨假設步進電機的脈沖當量為0.1mm，當前點為C（0，0），目標點為D（0.5，0.7）或D（0.7，0.5），圖3為經MATLAB仿真得到逐點比較法的運動效果圖，圖中的細線代表實際走過軌跡，粗線代表理想軌跡，由圖3我們可以明顯的看出，從一點到另一點，由于機構只沿著X或Y軸運動存在很大的誤差，而且插補效率很低。

圖2 逐點比較法運動判斷圖

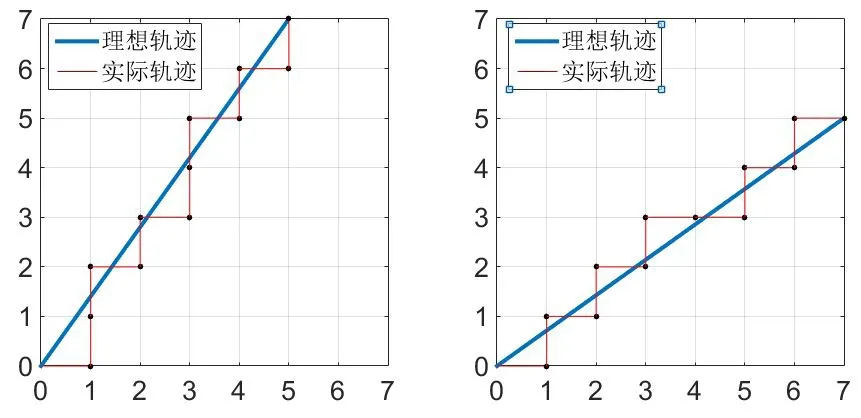
圖3 逐點比較法運動效果

2.2 最小偏差法

最小偏差法和逐點比較法的執行步驟、判斷依據基本一致，有所不同的是最小偏差法引入了不止沿著x軸和y軸插補，還引入了45度角插補，共把一個平面區域分成了八個卦限[7]，其各卦限進給方向和偏差關系如表2所示，在具體卦限的具體進給方向和偏差判斷如圖4所示，F為偏差，F≥0時，擠出機構沿Y=X或Y=-X運動，F＜0時擠出機構沿著X或Y軸運動，步進電機M1和M2以相同的速度順時針或逆時針同向轉動時，就可以沿著X軸運動，步進電機M1和M2以相同的速度順時針或逆時針反向轉動時，就可以沿著Y軸運動，當步進電機M1轉動，步進電機M2靜止時，滑塊將沿著Y=X方向移動；當步進電機M2轉動，步進電機M1靜止時，滑塊將沿著Y=-X方向移動。

同樣以0.1mm為步進電機的脈沖當量，假設當前點為C（0，0），目標點為D（0.4，0.7）或D（0.7，0.4），經過MATLAB仿真得到最小偏差法運動效果圖5，圖中的細線代表實際走過軌跡，粗線代表理想軌跡，由圖5可知，最小偏差法比逐點比較法在效率和精度上有了明顯的提高，但依然存在著較大的誤差，效率也并不高，所以現在就引入改進算法。以上兩種算法只局限于沿著X軸、Y軸和45度方向進給，其他角度的直線只能靠插補來實現。我們不妨假設，可以沿著其他角度插補，這就需要兩個步進電機同時以不同的速度運動，這樣就可以實現各種角度的高精度、高效率運動。

表2 最小偏差法插補公式表

圖4 最小偏差法運動判斷

圖5 最小偏差法運動效果圖

2.3 改進算法

2.3.1 原理描述

為了實現機構X、Y軸的聯動，需使電機M1和M2同時以不同速度運動，同時開始同時結束，其第一卦限運動示意圖如6所示。

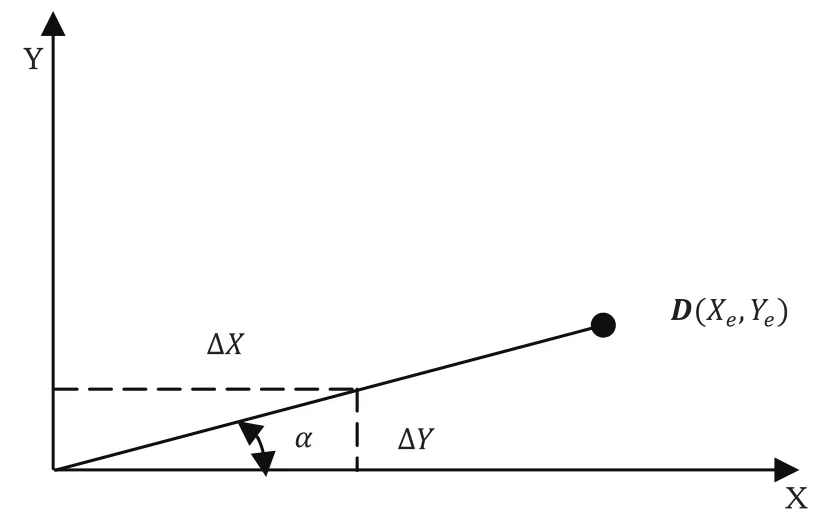
圖6 改進算法運動示意圖

由圖6可知，對于任意方向的直線插補，ΔX和ΔY的大小并不一定相同，此時：

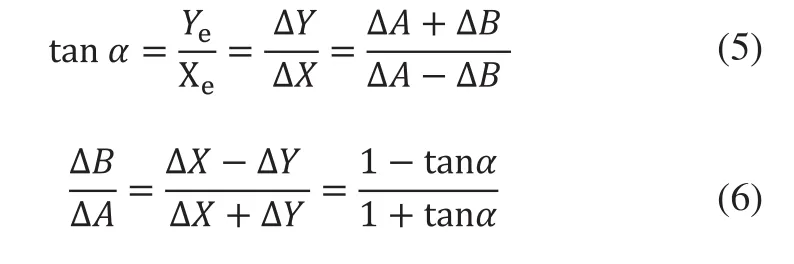
由此我們可以得到兩個步進電機的轉動的線位移的比例關系，兩個電機需要在相同時間完成轉動，所以電機的位移之比等于角速度之比，又由于步進電機的角速度ω1、ω2是由控制器輸出的脈沖的周期T1、T2決定，所以可得：

由式(7)可知我們可以通過控制其輸出脈沖的周期以達到控制機構滑塊沿著任意方向運動。

這種方法的難點在于周期大小選擇，脈沖周期過大和過小都會無法驅動步進電機，所以我們可通過設置及極限值的方法來限制不合適的脈沖，步進電機可以平穩驅動的脈沖周期大約為10μ s～3ms，對于128細分的驅動器，最小的驅動周期可達3μs；對于普通的驅動器沒有那么多細分，由式(7)可知，當直線方向接近Y=X時，驅動步進電機M2的脈沖周期則趨于無窮大，這樣這種方法就會產生死區，為了解決這一缺陷我們可以采取和最小偏差法相結合的方法，在死區時采用最小偏差法，其他時候采用這種方法，這樣就會大大提高機構的運動速度和精度。

2.3.2 算法實現步驟

對于算法的實現，需要確定CoreXY機構兩個步進電機的旋轉方向、驅動脈沖周期以及脈沖數目，因此可以分為以下3個步驟：

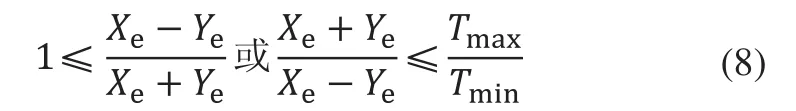
若符合要求，則適用改進算法；若不符合，則適用最小偏差法。

2）電機方向和步數確定：步進電機的轉動方向和轉動步數可以由下式確定：

式中X、Y為擠出機構沿X軸和Y軸脈沖當量的數目，可以通過Xe，Ye分別除以脈沖當量得到，A、B分大小別為步進電機M1和M2所需轉動的脈沖數，符號代表步進電機的轉動方向。

3）電機脈沖周期確定：由式(7)可以確定步進兩個步進電機脈沖周期之比，通常以周期較小者為基準周期，基準周期選用可平穩驅動步進電機的最小周期Tmin。

假設取當前點為C（11.3，-8.4），目標點為D（12.5，-8.7），脈沖當量為0.01mm，規定最小周期Tmin=0.5ms，最大周期Tmax=2.5ms，則易得Xe=1.2，Ye=-0.3，換算為脈沖當量數目為X=120，Y=-30，方向為第四象限。

（1）由式(8)知Xe，Ye在不等式范圍內，適用改進算法。

（2）由式(9)、式(10)計算得A=90，B=150，步進電機M1的需要轉動的脈沖數為90，方向為逆時針，步進電機M2的需要轉動的脈沖數為150，方向為逆時針。

3 結束語

我們分析了CoreXY機構的運動特性以及基于該機構3D打印機的常用運動控制算法，對比的各種算法的優缺點，提出了一種改進算法，運用這種算法，配合數據校正算法，再配合步進電機的梯形加減速算法[8]，PID算法控制擠出絲的溫度，配合Z軸和E軸的運動，可以獲得很好的打印精度和速度。