沖擊載荷下磁流變阻尼器單神經元PSD算法研究

黃 繼，高 佳，段承君，張 浩，韓曉明

(1.山西大學 自動化系，山西 太原 030002；2.山西大學 電力工程系，山西 太原 030002；3.西北機電工程研究所，陜西 咸陽 712099；4.中北大學 機電工程學院，山西 太原 030051)

磁流變阻尼器在結構上比傳統(tǒng)的液壓阻尼器簡單,體積小，方便安裝，并且相對于彈簧或液壓阻尼器結構一旦確定則阻尼力不可調的缺點，磁流變阻尼器能夠輸出可實時調節(jié)、變換范圍寬的阻尼力，且動態(tài)響應迅速，可在毫秒級的時間內完成緩沖動作。這完全符合自動武器系統(tǒng)后坐力阻尼器半主動控制的要求，具有很大的優(yōu)勢，因此在自動武器系統(tǒng)后坐力阻尼器半主動控制領域有著良好的應用前景[1-4]。

近年來，大量學者針對磁流變阻尼器的半主動控制提出了多種控制策略，包括滑膜控制、優(yōu)化控制、神經網絡PID控制、自適應控制以及線性二次高斯(LQG)同位控制策略等，均取得了令人滿意的控制效果[5-8]。但這些算法的實現均非常復雜，不便于計算機編程實現，對自動武器后坐緩沖控制來說，實時性上均無法保證。對此筆者提出了基于單神經元自適應PSD控制方法，這種算法結構簡單，通過編程很容易在計算機上實現，并且對被控對象參數、時滯變化不敏感，可有效提高系統(tǒng)的實時性和魯棒性[9]。

1 沖擊載荷下磁流變阻尼器受力分析

由于磁流變阻尼器是一個強非線性、大時滯的系統(tǒng)，為減小計算量，在不影響控制效果的前提下，對阻尼通道作如下假設[1-3]：

1)阻尼器的阻尼通道內始終充滿不可壓縮的磁流變液。

2)磁流變液在活塞工作過程中不會產生氣泡。

3)磁流變體在磁流變液中不會產生沉降，且均勻分布。

4)阻尼通道沿磁極中心線對稱，阻尼通道間隙的大小遠小于缸體內徑。

5)活塞運動時的速度和磁流變液流速有確定的數學解析關系，磁流變液流動方向與活塞運動方向平行，其他方向上沒有速度分量。

當沖擊載荷作用在阻尼器上時，磁流變液在壓力作用下被擠入環(huán)形的阻尼通道，由于磁流變液本身具有粘性，因此，在磁流變液內部以及磁流變液與阻尼孔壁之間會產生一個和活塞運動速度成正比的粘滯性阻力F1;經流體力學分析，磁流變液在沖擊載荷作用下，會由于流經的橫截面突變而產生一個和活塞運動速度的平方成正比的節(jié)流阻力F2；磁流變液流動時，會因為自身質量帶來的慣性，產生和活塞運動加速度成正比慣性阻力F3；同時，由于介質之間的耦合關系，會產生一個綜合阻力F4，因其較小，故忽略。總阻尼力中的上述成分，均和磁流變液性質及磁流變阻尼器結構及活塞運動速度有關，這些由物質本身物理特性和運動特性決定的力屬于不可控力。最后一部分是由于磁流變效應而產生的庫倫阻力FMR，可以通過改變磁場電流大小進而改變磁場強度而實現阻尼力的改變，它和磁流變液的屈服應力成正比，這部分力是實現磁流變阻尼器阻尼力可控的基礎[1]。

通過分析,得到磁流變阻尼器所提供的阻尼力的動力學模型為:

(1)

式中，ρ1、ρ2、ρ3、ρMR分別為各分量的比例系數，它們只與磁流變液特性以及磁流變阻尼器結構有關。

2 自動武器緩沖過程分析

設炮膛合力為Fpt，磁流變阻尼器產生的總阻尼力為FR，炮體復進時由復進簧產生的復進簧力為Ff，緩沖系統(tǒng)內的摩擦力為f，包括導軌上摩擦力和密封裝置摩擦力等，m為武器后坐部分的質量，v為后坐時的速度，θ為射角，則在后坐過程中，有[1,2,10]：

(2)

在復進過程中，有：

(3)

對于復進簧，有：

Ff=Ff0+kx,

(4)

式中：Ff0為復進簧初力；k為彈簧剛度系數；x為位移。

因此，得出自動武器磁流變阻尼器緩沖系統(tǒng)動力學模型為[1]：

后坐時，

kx+f-mgsinθ)；

(5)

復進時，

ρMRτy-f-mgsinθ).

(6)

3 單神經元自適應PSD算法設計

基于單神經元PSD算法的控制器機構框圖如圖1所示，通過加權系數wi對輸入xi進行加權，由圖可知，對加權系數wi進行實時在線調整，即可實現控制器的自組織與自適應功能。

加權系數由式(7)確定：

(7)

式中：e(k)是誤差反饋信號；z(k)是教師訓練信號，本設計中，取z(k)=e(k)；δI為積分學習速率；δP為比例學習速率；δD為微分學習速率。

在學習過程中，為了提高系統(tǒng)收斂速度，可以在xi(k)1.04×xi(k-1)時，可以減小學習速率，此時，選δi(k)=0.75δi(k-1)，達到穩(wěn)態(tài)后，可選δi(k)=δi(k-1).

圖1中，xi作為控制器的輸入，分別取作系統(tǒng)的誤差、誤差的一次差分和誤差的二次差分[9]，即:

(8)

由圖1得控制器的輸出及學習規(guī)則可表示為[9-10]：

(9)

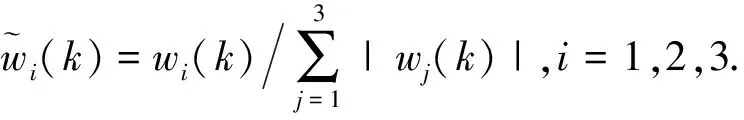
4 仿真和實驗驗證

為了驗證本算法在沖擊載荷下磁流變阻尼器控制中的有效性和可靠性，首先，在Simulink中進行仿真驗證。仿真模型如圖2所示，包括單神經元PSD控制器，阻尼器動力學模型以及沖擊載荷輸入3個部分，其中，利用S-Functions來實現沖擊載荷和控制器兩個部分。

所研究的磁流變阻尼器結構參數如表1所示。

表1 磁流變阻尼器仿真系數

將表1數據帶入阻尼器動力學模型，得動力學模型參數為：

ρ1=213.11,ρ2=19.25,ρ3=1.05,ρMR=0.16.

圖3為控制系統(tǒng)的位移-時間曲線，圖4為控制系統(tǒng)的后坐力-時間曲線。在控制算法作用下，磁流變阻尼器的最大位移為38 mm，與此同時，后坐力峰值為9.8 kN，最大超調量為1.25%.由圖3、4中可以看出，在阻尼器作用下，后坐位移變化平緩，并實現了后坐力“平臺”效應，表明磁流變阻尼器后坐緩沖系統(tǒng)具有較強的耗能減震效果，本文的PSD算法對大時滯強非線性的磁流變阻尼器具有很好的控制性能。

為進一步驗證本算法對磁流變阻尼器的控制性能，搭建了由彈簧壓力機、磁流變阻尼器以及控制及測量系統(tǒng)構成的實驗平臺，如圖5所示。 通過控制系統(tǒng)向阻尼器施加不同強度的電流，觀察阻尼器提供的阻尼力，來驗證本算法的可行性。

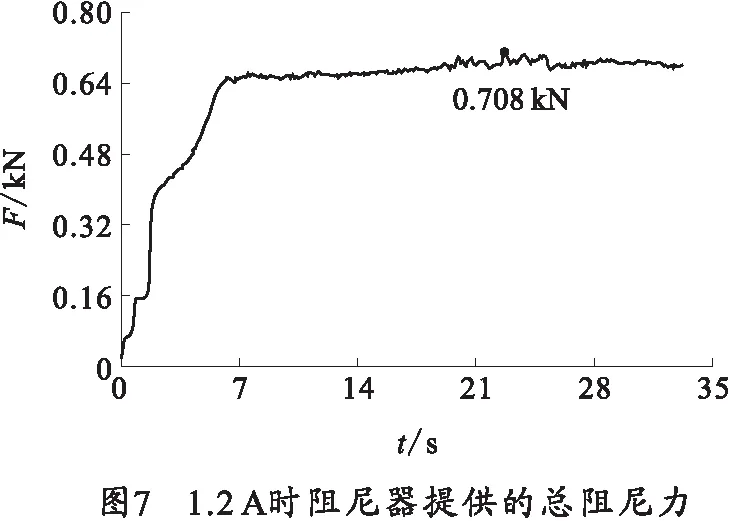
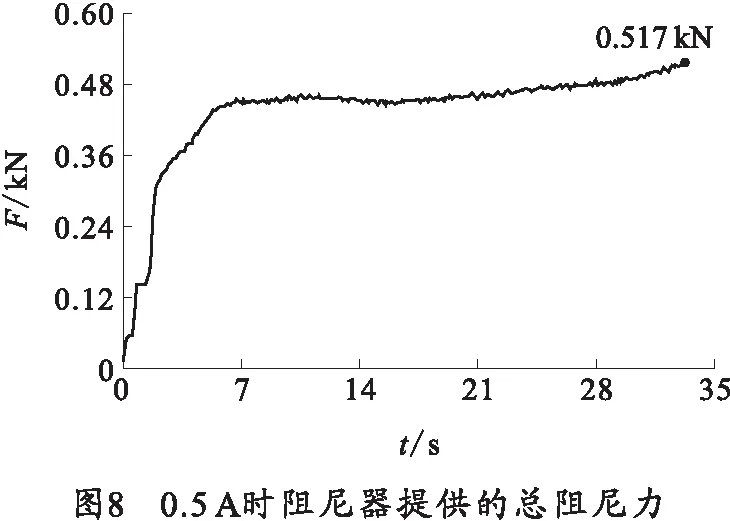
彈簧壓力機上實驗結果如圖6～8所示。圖6～8分別為1.6 A時阻尼器提供的總阻尼力，1.2 A時阻尼器提供的總阻尼力，0.5 A時阻尼器提供的總阻尼力以及阻尼力的變化過程。由圖6～8中可以看出，阻尼器在沖擊載荷作用下，提供的阻尼力迅速升高并很快達到穩(wěn)定值，同時，隨著控制器輸入電流的增加，磁流變阻尼器提供的阻尼力也在升高，有效的實現了“平臺”效應，并延長了“平臺”的寬度。

5 結束語

為了解決自動武器緩沖后坐過程不可控的問題，筆者將磁流變阻尼器應用于自動武器緩沖控制系統(tǒng)。首先對阻尼器進行動力學建模，得到了對阻尼器提供的總阻尼力模型，分析了其中的可控部分，在此基礎上，利用單神經元PSD控制算法魯棒性強，算法簡單，易于實現的特點，將其應用在磁流變阻尼器控制中，由仿真和實驗平臺驗證可以看出，本算法發(fā)揮了其全局性能優(yōu)越，魯棒性強的特點，有效的實現了后坐“平臺”效應，達到了滿意的控制效果。

磁流變液作為新型智能材料，對它的應用研究還存在很多亟需解決的問題。國外研究證明，當磁流變液流速過快超過一定閾值，阻尼力變得不再可控，而在高射速自動武器反沖后坐過程中，這一現象必然會對后坐力的控制產生重要

影響，在以后的分析研究中，必須考慮這一效應。同時，為了簡化阻尼器動力學模型，筆者將阻尼器作為單自由度系統(tǒng)來分析，在今后的研究中，必須考慮其在整個自動武器中的動態(tài)特性，將其放在整個緩沖后坐系統(tǒng)中進行整體分析。