基于二維修正組件的彈道修正彈穩定性分析與仿真研究

柯知非，高 敏，王 毅，宋衛東

(陸軍工程大學石家莊校區，河北 石家莊 050003)

彈道修正彈是指利用彈道修正技術對傳統彈藥進行信息化改造的彈藥，它的特點是可大量裝備部隊、具有一定打擊精度、高效費比。問世之后，彈道修正彈便成為各國關注和爭相研究的熱點，國內外許多專家學者也就彈道修正彈的設計提出了許多不同的方案[1-3]。

在各種設計方案中，需要解決的核心問題是要在滿足彈丸的穩定性的基礎上最大限度的提高修正能力。而由于修正執行機構的存在，彈丸的氣動布局會發生較大的改變，必須對其穩定性進行考核與評估。

旋轉穩定彈丸無控狀態下的穩定性分析一般都借助美國學者Murphy所建立的角運動理論，通過陀螺穩定因子和動態穩定因子等判斷普通榴彈的穩定性。

揭濤等針對CCF模式的雙旋榴彈建立了多剛體彈道模型，并直接用傳統的穩定性判據對彈丸的穩定性進行了分析[4]。然而，傳統的穩定性判據是否能直接判斷雙旋榴彈的穩定性需要研究。王志剛、李偉等針對基于固定鴨舵的彈道修正火箭彈進行了彈道建模，并通過角運動方程分析了火箭彈的穩定性[5-6]。常思江、王中原等通過數值仿真的手段檢驗了彈丸有控和無控狀態下的穩定性[7]，之后，常思江對共振穩定性進行了研究，對大攻角條件下的前體轉速閉鎖問題進行初步分析，導出了該彈發生轉速閉鎖的穩定方位角及臨界攻角表達式[8]。鐘揚威等基于Kane方法建立了雙旋彈飛行動力學模型，并通過編程對雙旋彈的無控和有控運動特性進行了仿真分析，得出雙旋彈無控時以小迎角穩定飛行；有控飛行時彈體產生配平迎角，且縱向和橫向修正會產生交叉耦合的結論[9]。張衍儒等通過分析雙旋靜穩定彈角運動方程，討論了共振不穩定的特性，得出固定翼鴨舵的轉速及雙圓運動頻率影響攻角運動[10]。

筆者在前人對修正彈彈道模型研究的基礎上，建立二維彈道修正彈剛體彈道模型，描述出彈丸的動力學和運動學關系。通過穩定性理論和判據分析剛體彈道模型，得出滿足穩定性應具備的條件，并研究了有控與無控狀態下舵結構參數對穩定性的影響。

1 彈道建模

發射系內建立的運動方程組用于彈道解算。首先建立彈丸質心的運動方程組，然后依據修正組件和彈體的繞彈丸質心的轉動描述彈丸繞質心轉動的方程組，依據兩剛體的運動學關系可將所建立的方程簡化，建立描述彈丸運動狀態的彈道模型。

1.1 彈丸受力分解

修正組件和彈體的馬格努斯力垂直于總攻角平面，而馬格努斯力矩在攻角平面內，分別將其轉換到準彈體坐標下，得表達式如下：

(1)

1.2 發射系下運動方程組的建立

飛行過程中，彈丸的運動狀態通過彈丸質心的運動和繞質心的轉動來描述。將彈丸質心的運動描述在發射系下，即彈丸質心的速度、位置信息均在發射系下投影，利用該方式進行彈道解算，便于與實際飛行狀態下的彈丸速度、位置信息相對比，是當前彈道解算的常用方法。將彈丸繞質心的轉動建立在準彈體坐標系下，形式最為簡單。建立描述彈丸運動狀態的運動方程組如下：

(2)

式中所使用的坐標系及角度定義可參考文獻[11]，Mfax4、Mafx4分別為修正組件和彈體間相互作用力矩在準彈體系x4軸上的分量，該力矩包括軸承間的摩擦力矩和制動過程中的控制力矩。

1.3 繞彈丸質心的轉動方程組

1.3.1 彈丸繞質心轉動的動力學方程組

彈丸繞質心運動的動力學方程組為：

(3)

式中：Jfx、Jfy、Jfz為修正組件相對彈丸質心的轉動慣量在準彈體上的投影；Jax、Jay、Jaz為彈體相對彈丸質心的轉動慣量在準彈體系上的投影；ωfx4、ωy4、ωz4為修正組件的角速度在其準彈體系上的投影；Mfx4、Mfy4、Mfz4為修正組件所受氣動力矩在準彈體上的投影；Mfax4、Mfay4、Mfaz4為彈體對修正組件作用的力矩(包含控制力矩)在準彈體上的投影；ωax4、ωy4、ωz4為彈體角速度在其準彈體系上的投影；Max4、May4、Maz4為彈體所受氣動力矩在準彈體系上的投影；Mafx4、Mafy4、Mafz4為修正組件對彈體作用的力矩(包含控制力矩)在準彈體上的投影。

1.3.2 彈丸繞質心轉動的運動學方程組

彈丸姿態使用俯仰角φ、偏航角ψ、修正組件滾轉角γf和彈體滾轉角γa4個變量來描述。設準彈體坐標系相對于地面發射系的轉動角速度為ω′，整理后，可得：

(4)

2 穩定性分析

彈丸飛行穩定是進行彈道特性分析和控制系統設計的前提。安裝二維彈道修正引信后，彈丸的飛行包括有控和無控兩種狀態。無控狀態下飛行的彈丸近似于在普通彈丸頭部施加一周期與修正組件轉速相同的擾動力，而有控狀態下飛行的彈丸近似于普通彈丸頭部施加一方向和幅值變化的控制力，該力將降低彈丸的穩定性。

2.1 陀螺穩定性

旋轉穩定彈丸是靜不穩定彈丸，即彈丸所受氣動力的壓心在彈丸質心之前，氣動力形成的靜力矩將使彈丸軸線偏離合速度形成攻角，稱該力矩為翻轉力矩。彈丸的高速旋轉使其具有定軸性，保持了彈丸穩定性。

在所有的氣動力矩中翻轉力矩占主導地位，只考慮靜力矩項的角運動方程的齊次方程為

Δ″-iPΔ′-MΔ=0.

(5)

可得方程特征根為

(6)

令Sg=P2/4M，稱其為陀螺穩定因子，則彈丸穩定的條件為Sg>1.

當彈丸處于無控狀態時，陀螺穩定因子可整理為：

(7)

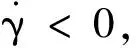
即陀螺力矩項的減小量大于靜力矩項的減小量，造成陀螺力矩項與翻轉力矩項的比值減小。因而，與普通榴彈相比彈體的轉速需更高才能使彈丸穩定，即彈丸的穩定性在安裝修正組件后有所降低。

當彈丸處于有控狀態時，陀螺穩定因子可整理為：

(8)

由式(8)知，有控狀態下彈丸的靜力矩項比普通彈丸增加了翻轉力矩項kc，使靜力矩項增大，從而造成陀螺穩定因子的減小，降低彈丸的穩定性。

圖1為修正彈在無控和有控狀態下的陀螺穩定因子Sg的曲線。圖中，兩條曲線在全彈道上均滿足Sg>1的陀螺穩定條件。

2.2 追隨穩定性

在彈丸飛行過程中，由于重力作用彈丸的質心速度將會逐漸向下偏轉，但其不會使彈軸偏轉，因而產生俯仰平面內的攻角。必須存在作用在彈軸上的力矩才能使彈軸跟隨彈丸合速度方向的偏轉，否則，彈丸總攻角將增大，導致近彈現象的出現。

對于旋轉穩定彈，在彈丸飛行過程中將出現動力平衡角，且該角在水平方向的分量約是豎直方向分量的10倍，在其產生的氣動力作用下產生垂直于彈軸向下的翻轉力矩，迫使彈軸向下偏轉，形成彈軸跟隨質心合速度的現象。然而，動力平衡角過大將使彈丸穩定性降低，飛行特性變差，散布加大，甚至使射程大大減小。為使彈丸具有良好的彈道特性，需要限制動力平衡角的大小。動力平衡角最大值出現在彈道頂點附近，故只需限制最大射角發射彈丸時的彈道頂點處得動力平衡角即可。

圖2為修正彈在有控和無控狀態下的總攻角曲線。

需要指出的是，彈丸以52°射角出炮口，在40 s起控，且其控制角穩定在180°直至彈丸落地。圖2中，彈丸起控后總攻角曲線出現了較大的抖動，隨著彈丸的繼續飛行抖動幅值逐漸減小。總攻角曲線的平均位置即為彈丸的動力平衡角，故有控狀態下其動力平衡角不會超過3°，無控狀態下動力平衡角不超過2.7°，說明該彈丸滿足追隨穩定條件。

2.3 動態穩定性

考慮彈丸所受的全部氣動力和氣動力矩時，彈丸角運動方程的齊次方程的特征根的表達式如下：

(9)

當彈丸處于無控狀態時，

(10)

當彈丸處于有控狀態時，

(11)

令

(12)

式中，Sd為動態穩定因子。

通過討論Sdd的值即可判斷彈丸的動態穩定性。圖3和圖4分別為無控和有控狀態下動態穩定因子Sd和Sdd的曲線。圖4中兩條曲線均在0上方，說明該彈丸在有控和無控狀態下均處于穩定狀態。

2.4 共振穩定性

在彈丸的無控飛行中，修正組件在來流作用下繞彈軸自由旋轉。由于修正組件氣動外形不對稱，將產生周期性作用力。若該周期性作用力的頻率與彈丸自由擺動周期相同將發生共振，使彈丸攻角急劇增大，造成彈丸失穩，稱該種不穩定為共振不穩定。

彈丸飛行過程中，在某一較小時間段內彈丸合速度及所受氣動力不變，角運動方程為常系數線性微分方程，其解滿足疊加性，故可單獨討論控制力項對角運動的影響。

無控狀態下，僅考慮控制力矩項的角運動方程為

Δ″+(H-iP)Δ′-(M+iPT)Δ=B′eiχs，

(13)

可得方程的通解為

Δ=C1e(λ1+iω1)s+C2e(λ2+iω2)s+Δt.

(14)

隨彈丸的飛行二圓運動將衰減至消失，僅剩下周期性氣動力產生的受迫圓運動。定義修正組件不旋轉時，彈丸在常值干擾力下產生的攻角為定常攻角，易得該定常攻角為

(15)

定義穩定強迫振動的振幅與定常攻角的幅值的比值為放大系數，則有

(16)

圖5為無控和有控狀態下角運動的頻率曲線。圖中，無控和有控狀態下的快慢圓運動頻率分別相等(誤差較小)，快圓運動頻率ω1不超過0.5 rad/s，慢圓運動頻率ω2小于0.1 rad/s.

為維持彈丸的穩定性，彈體高速旋轉，其滾轉頻率遠大于二圓運動頻率。修正組件在無控狀態下的穩定轉速約為30 r/s，遠大于兩頻率值；有控狀態下，理想狀態時修正組件相對地面穩定在某一控制角度，轉速為0.控制算法的不同對修正組件的轉速要求也不同，在修正組件減旋期間會經過共振區。因此，需要對控制算法和組件執行機構提出了更高的要求。

3 案例分析與仿真

安裝二維彈道修正引信的旋轉穩定榴彈的穩定性分析包括陀螺穩定性分析、動態穩定性分析、追隨穩定性分析、共振穩定性分析等。在理想狀態下，彈丸滿足共振穩定性，然而在修正引信的制動控制中該問題必須被考慮。彈丸的追隨穩定性是指彈軸追隨質心的合速度方向，在彈丸落地時實現彈丸頭部著地。陀螺穩定性是榴彈穩定的必要不充分條件。在彈丸動態穩定性分析過程中，陀螺穩定因子是該過程必不可少的因素。動態穩定性是彈丸飛行穩定的充要條件，滿足動態穩定性條件的彈丸必定飛行穩定。下文重點討論舵結構參數與初始擾動差異對安裝二維彈道修正引信的彈丸的動態穩定的影響。

仿真中所選用的氣象條件為標準氣象條件，彈丸初速為890 m/s，射角為40°,仿真所得落點如表1所示。

表1 不同舵結構參數的彈丸仿真落點坐標

3.1 無控狀態下舵結構參數對穩定性的影響

無控狀態下，彈丸的動態穩定條件如下：

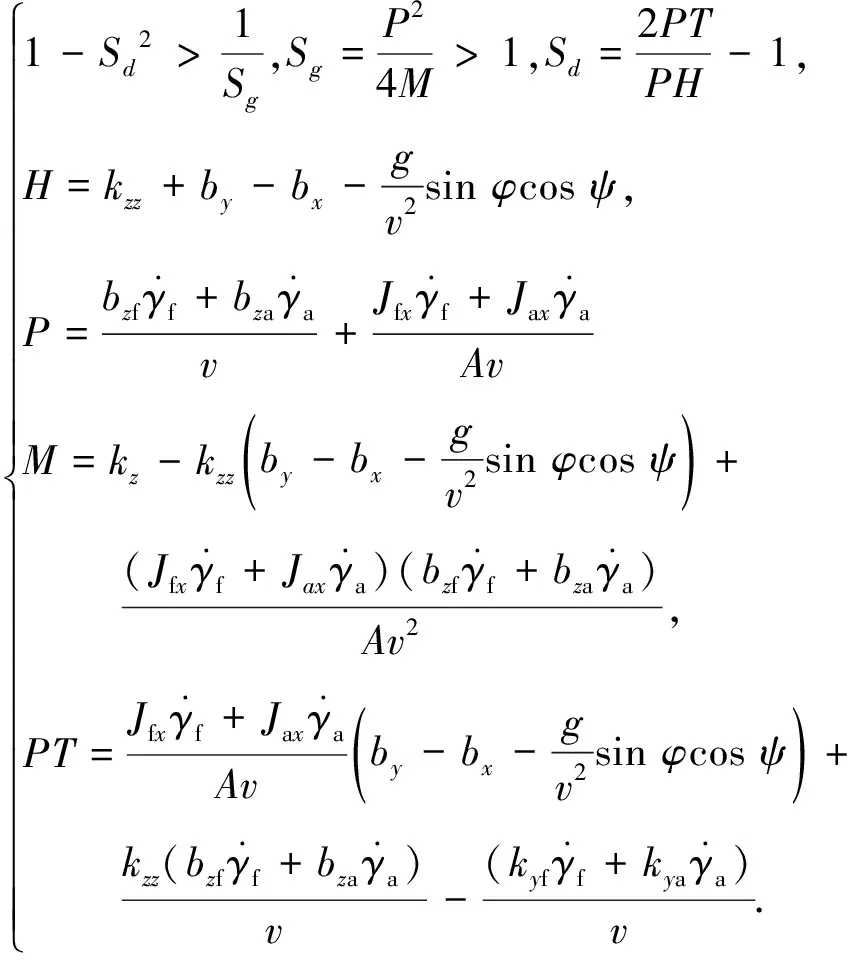
(17)

舵結構參數對彈丸的射程、側偏、動力平衡角、舵轉速、彈體轉速、質心合速度等都有影響。由式(17)可知，上述因素對彈丸的穩定性存在不同程度的影響，因而，很難定量分析舵結構參數對彈丸穩定性的影響。

通過仿真的手段分析舵結構參數對彈丸穩定性的影響，給出不同舵結構參數的彈丸的陀螺穩定因子Sg和Sdd隨時間的變化曲線，如圖6、7所示。其中4°和6°是指在發射之前將同向控制舵預先調至該角度。

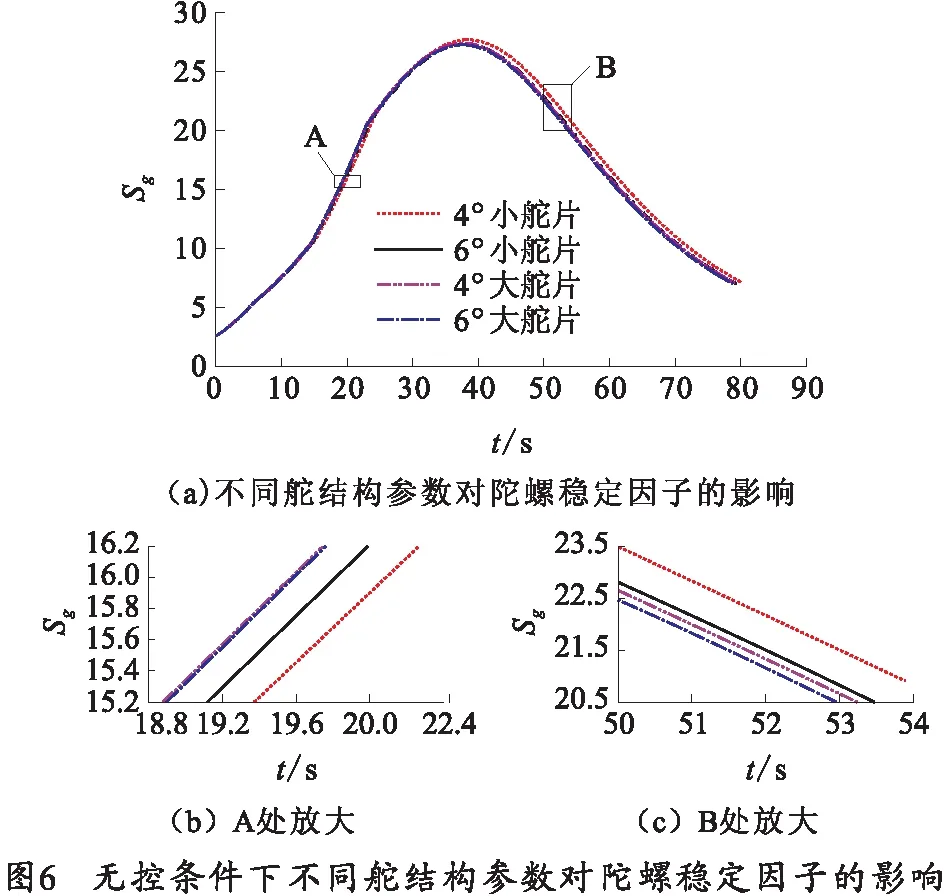
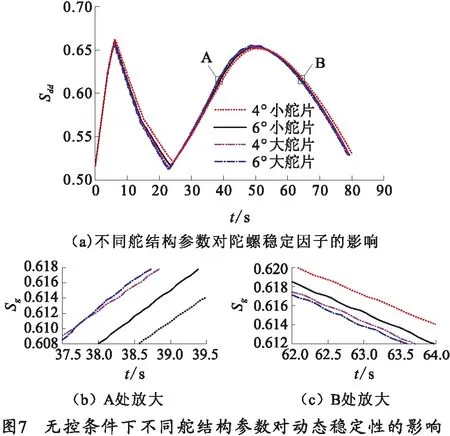
圖6中，不同舵結構參數的彈丸的Sg的曲線均呈現先增大后減小的趨勢，且Sg沿全彈道均大于1，說明彈丸均滿足陀螺穩定條件。彈道升弧段，陀螺穩定因子由大到小依次為4°大舵片、6°大舵片、6°小舵片、4°小舵片；彈道降弧段，陀螺穩定因子由大到小依次為4°小舵片、6°小舵片、4°大舵片、6°大舵片。

圖7中，不同舵結構參數的彈丸的Sdd曲線具有相同的變化趨勢，且其值沿全彈道均大于0，說明彈丸滿足動態穩定條件。彈道起始段(0～7 s)，4種結構舵片穩定性很接近，之后(10～22 s)4°小舵片穩定性明顯高于另外3種結構舵片，30～50 s動態穩定性由大到小依次為6°大舵片、4°大舵片、6°小舵片、4°小舵片，60 s之后，動態穩定性由大到小依次為4°小舵片、6°小舵片、4°大舵片、6°大舵片，整個過程中，4°大舵片和6°大舵片的動態穩定性都很接近。

3.2 有控狀態下舵結構參數對穩定性的影響

有控條件下，彈丸的動態穩定條件如下：

(18)

與無控條件下的研究方法相同，采用仿真的手段研究舵結構參數對彈丸有控條件下彈丸的動態穩定性的影響,如圖8、9所示。

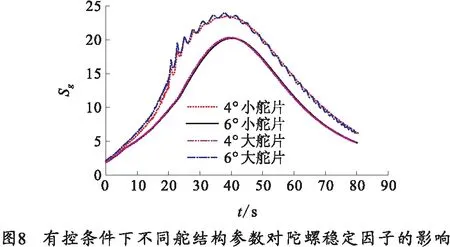
圖8中，不同舵結構參數的彈丸的Sg的曲線均呈現先增大后減小的趨勢，且Sg沿全彈道均大于1，說明彈丸均滿足陀螺穩定條件。4°小舵片和6°大舵片陀螺穩定因子很接近，4°大舵片和6°小舵片很接近，且前兩者明顯大于后兩者。

圖9中，不同舵結構參數的彈丸的Sdd曲線具有相同的變化趨勢，且其值沿全彈道均大于0，說明彈丸滿足動態穩定條件。4°小舵片和6°大舵片動態穩定性很接近，4°大舵片和6°小舵片很接近，且前兩者明顯大于后兩者。

4 結束語

筆者首先在理論上對彈道模型進行了穩定性分析，得到了滿足陀螺穩定性、追隨穩定性、動態穩定性與共振穩定性的要求。通過不同結構參數條件下舵對穩定性影響的仿真分析，可得出無控狀態下結構參數對穩定性的影響較小，而在有控制狀態下結構參數的改變對穩定性影響較大。