抽筒子疲勞裂紋擴展研究及剩余壽命預測

朱永梅， 姚 祥，倪路瑤，唐文獻，賈蘭俊

(1.江蘇科技大學 機械工程學院，江蘇 鎮江 212003；2.江蘇科技大學 江蘇省船海機械先進制造及工藝重點實驗室，江蘇 鎮江 212003；3.中國船舶重工集團公司第713研究所，河南 鄭州 450015)

現階段的火炮在服役時，經過一定發數后零部件上開始出現較微小的裂紋。隨著火炮的連續發射作業，該裂紋會逐漸生長。裂紋生長至臨界斷裂長度后，裂紋會開始快速擴展，該部件將會斷裂。較多事例表明，這種疲勞裂紋引發的機械部件的斷裂故障是十分常見的[1-2]。抽筒子是火炮射擊后完成抽筒動作的關鍵部件，由于受到沖擊載荷的作用，抽筒子會發生疲勞斷裂，導致炮彈發射后藥筒無法抽出，從而使火炮失去戰斗力，在實際射擊試驗中也多次發生過抽筒子斷裂的故障[3]。所以，為了提高火炮的安全性和可靠性，需要對抽筒子炮鋼材料的裂紋擴展性能和疲勞剩余壽命進行研究。

近年來，我國對火炮疲勞壽命的研究不斷深入，胡慧斌等[3]使用ADAMS建立了火炮的虛擬樣機，模擬發射工況，輸出抽筒子承受的載荷譜，結合材料的S-N曲線，建立了沖擊載荷作用下火炮抽筒子的疲勞損傷與壽命模型。朱超等[4]建立了自行火炮炮閂系統虛擬樣機模型，得到抽筒子爪在抽筒過程中的載荷譜,基于有限元技術建立了抽筒子有限元模型，對抽筒子進行了靜強度分析，進而利用疲勞分析軟件對抽筒子進行了疲勞壽命預測。易當祥[5]針對火炮行動系統的疲勞斷裂，采用邊界元法計算應力強度因子。Leonel等[6]采用了邊界配置法進行應力強度因子的計算。目前對于抽筒子的疲勞斷裂研究主要都是利用軟件進行仿真分析，但是在抽筒子產生裂紋的條件下，很少有關于剩余壽命的評估及計算方法進行研究的文獻。

筆者以某炮炮閂機構的抽筒子為研究對象，針對抽筒子材料45CrNiMoVA，開展室溫下斷裂韌度和疲勞裂紋擴展試驗，測試材料的斷裂韌度，結合實驗數據擬合得到Paris斷裂公式。根據抽筒子在抽殼工況下的受載情況，以Paris公式為理論依據，建立抽筒子剩余壽命計算模型，并討論了應力、初始裂紋長度和材料斷裂韌度3種因素對抽筒子的剩余壽命的影響，并得到它們的關系曲線。

1 疲勞裂紋擴展規律試驗

1.1 斷裂韌度實驗結果及計算

試驗設備采用美國MTS810-250 kN電液伺服熱機疲勞試驗機。按照0.8 mm/min的加載頻率加載至試樣斷裂，記錄完整的P-V曲線。試驗所用材料為45CrNiMoVA，室溫下的力學性能如表1所示。參照文獻[7]，采用三點彎曲試樣SE(B)，對其平面應變斷裂韌度進行試驗研究。

表1 45CrNiMoVA的力學性能

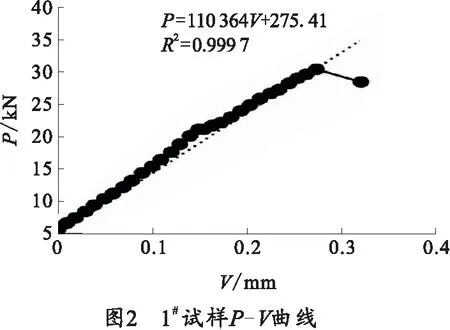
試驗選用4塊寬度為40 mm，厚度為20 mm的板材，分別標號為1#、2#、3#、4#，其中1#試樣的斷面放大圖如圖1所示，取厚度方向1/4、1/2和3/4三處從缺口到裂紋前緣的長度分別為a2、a3、a4，其平均值作為裂紋長度a。而且a2、a3、a4之間任意兩個測量值之差不得大于0.1a，若不滿足這些條件試驗結果無效。試驗所得的P-V曲線如圖2所示,因為45CrNiMoVA材料是高強度鋼，這種類型材料一旦產生裂紋后，裂紋尖端不能產生鈍化，會迅速發生擴展直至斷裂。根據文獻[8]臨界載荷FQ等于Pmax.

45CrNiMoVA材料的斷裂韌度試樣尺寸參數及試驗測得的結果如表2所示。

表2 45CrNiMoVA的力學性能

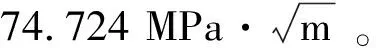
1.2 疲勞裂紋擴展速率試驗結果

根據抽筒子在抽殼工況下的應力分布情況，對試樣加載14～1 400 MPa的循環應力，試樣的應力加載方向與裂紋垂直，加載波形為正弦波，頻率為10 Hz，加載應力比取0.1。參照文獻[8]，采用標準拉伸C(T)試樣，厚度為12.5 mm，有效寬度為50 mm，試樣切口長度為12.5 mm，采用ΔK控制法得到預制裂紋長度為2.5 mm，試樣如圖3所示。

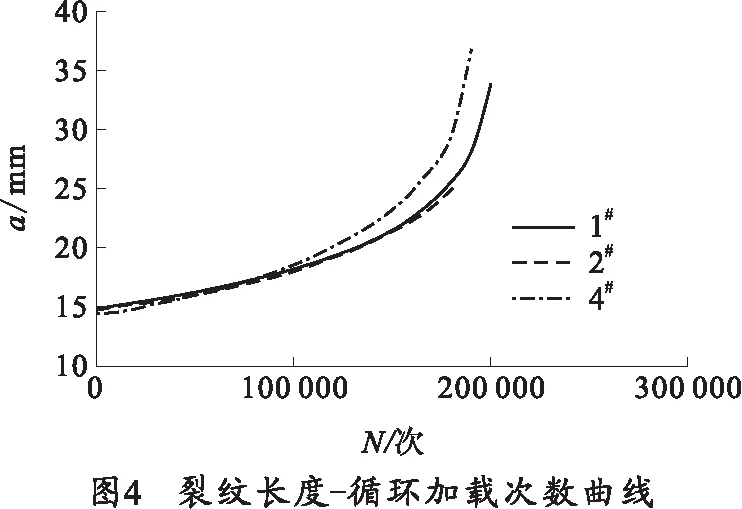
試驗采用4個C(T)試樣，分別記作1#、2#、3#、4#，并對試驗結果取平均值。由于3#試樣在試驗開始時發生裂紋橫向萌生，結果無效，其他試樣的疲勞裂紋擴展量a與反復加載次數N的關系如圖4所示。

由圖4可知，在橫幅循環載荷作用下，裂紋長度在14.85 mm左右開始發生擴展，隨著加載次數的遞增，裂紋擴展速率緩慢增加，在加載次數約135 000次以后，裂紋擴展速率快速增大，裂紋快速擴展，直至發生斷裂，3個試樣從裂紋發生擴展到斷裂時加載次數為180 000～200 000次，最終裂紋長度為24.79～37.14 mm.

1.3 疲勞裂紋擴展速率計算

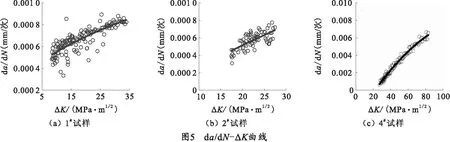
將1#、2#、4#試件的試驗數據，擬合成裂紋擴展速率和應力強度因子的關系，如圖5所示。其中，2#試樣的無效點很多，3組試驗數據在對數坐標系中均呈線性相關，且變化趨勢一致。可以看出該炮鋼的疲勞裂紋擴展速率隨應力強度因子的增大而提升。

Paris疲勞裂紋擴展速率為

da/dN=C(ΔK)m,

(1)

式中：a為裂紋長度；N為應力循環次數；da/dN為裂紋擴展速率；ΔK為應力強度因子變化幅值；C和m均為材料常數，由實驗數據測得：

(2)

式中：Kmax為抽筒子的應力強度因子最大值；Kmin為最小值，由于抽筒子承受的是沖擊載荷，Kmin則為0；α為形狀因子；Δσ為應力幅值。

根據曲線擬合得出C和m的值，如表4所示。由于45CrNiMoVA材料為高強度炮鋼，硬度、強度較大，試驗時受外部因素影響較大，容易出現表3所示m值波動大的現象。

表3 裂紋擴展試驗結果

計算平均值，取C為2.578×10-11，m為2.859，查閱材料手冊[9]得知，45CrNiMoVA材料的C=2.614×10-12，m=2.827，與試驗的計算結果對比可知，m值相差不大，但C值相差較大，比查閱值大了約10倍。因為在疲勞裂紋擴展后期，裂紋長度及尖端的強度因子較大時，慣性致使尖端振幅高于試驗所需要的幅值，使裂紋擴展速率變快，這可能是造成數據偏差的主要原因。通過閱讀文獻[10]，發現其他研究者在計算材料C和m值時也會存在一定的偏差，因此在后面的計算中采用本試驗得到的C和m值。所以，45CrNiMoVA材料的Paris斷裂公式為

da/dN=2.578×10-11(ΔK)2.859.

(3)

2 抽筒子剩余壽命估算

2.1 疲勞裂紋剩余壽命估算理論依據

根據斷裂力學理論，將疲勞裂紋擴展分為3個區域：第I區為裂紋不擴展區，此時ΔK<ΔKth，其中ΔKth為疲勞裂紋擴展門檻值；第II區為裂紋臨界擴展區，此階段為估算疲勞裂紋剩余壽命的主要區域；第III區為裂紋快速擴展區，裂紋擴展速率極高，裂紋擴展壽命極短，可忽略。

疲勞裂紋擴展速率da/dN-ΔK曲線僅受材料自身、加載條件、試驗環境等影響，不會因為試樣的形狀或尺寸產生變化。本文通過試驗獲取的Paris斷裂公式(3)來預測出抽筒子疲勞裂紋擴展壽命。

當應力強度因子幅值ΔK比疲勞裂紋門檻值ΔKth大，裂紋將發生擴展，否則，裂紋不擴展；即：

ΔK>ΔKth,

(4)

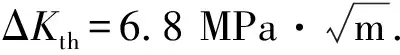
現有的研究表明[11]，使用各種測試方法得到的初始裂紋尺寸為0.05～0.50 mm.因此本文在預測抽筒子剩余壽命時將抽筒子初始裂紋尺寸確定為a0=0.5 mm.

將式(1)積分，可得疲勞裂紋擴展壽命計算公式，即從初始裂紋擴展到臨界裂紋的應力循環數為

(5)

臨界裂紋尺寸ac的取值可由裂紋處的應力強度因子及材料的斷裂韌性確定：

(6)

式中：KIC為材料的斷裂韌度；σmax為循環應力的最大值。

對于無限大板，形狀因子α和裂紋尺寸a無關，可得：

(7)

式中：C1=Cαmπm/2；Np為從初始裂紋尺寸a0擴展到臨界裂紋尺寸ac的應力循環數。

2.2 抽筒子疲勞裂紋擴展壽命

建立抽殼系統柔體動力學分析模型。通過抽殼系統的動力學分析得到，抽筒子在抽殼過程中分別與搖臂和藥筒發生碰撞，碰撞接觸處應力較大，超過材料的屈服極限，但只出現在接觸表面很小的一部分區域，且作用時間很短，準確性不高，對整體的結構不會產生很大的影響。所以筆者主要分析抽筒子中部的應力情況。

抽殼過程中抽筒子爪部與藥筒接觸部分所受最大載荷為38 kN[12].通過建立抽筒子等效有限元模型，得到其危險點應力云圖如圖6所示。

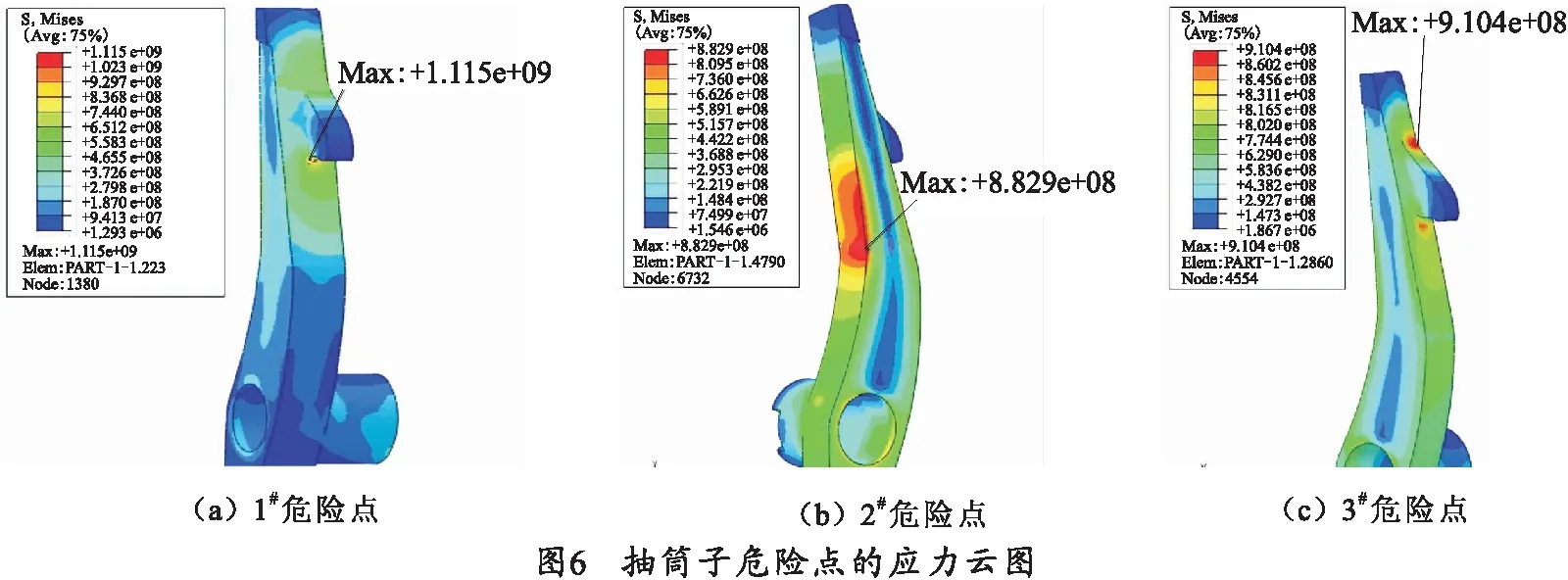
抽筒子的表面裂紋可視為單邊裂紋，形狀因子a為1.12，由式(6)可得臨界裂紋長度：

(8)

由式(8)求得最終抽筒子疲勞裂紋擴展壽命為

(9)

2.3 抽筒子剩余壽命影響因素分析

2.3.1 不同應力場下抽筒子的剩余壽命

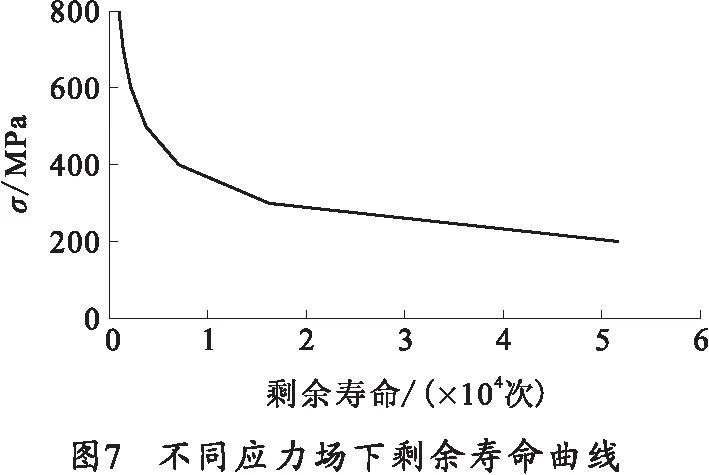
根據本文的試驗條件，初始裂紋長度確定為0.5 mm ,由上文計算得臨界裂紋長度為3.94 mm，通過剩余壽命預測模型可得應力與裂紋擴展壽命之間的S-N關系曲線，如圖7所示。由圖7可知所受應力越小的情況下，抽筒子的剩余壽命越大，且在應力為400～800 MPa區間內，剩余壽命增大緩慢，而在200～400 MPa區間內增大非常迅速，其中300 MPa時壽命為16 196次;200 MPa時壽命約為51 624次，增大了約3.2倍。

2.3.2 不同初始裂紋長度下抽筒子的剩余壽命

應力恒定為600 MPa時，改變已存在的裂紋長度得到該裂紋的剩余壽命，計算得出的關系曲線如圖8所示。由圖8可知應力恒定時，當初始裂紋長度從0.5 mm增大到1 mm時，剩余壽命減小幅度最大，減小了約1.8倍(約1 000次)。

2.3.3 不同斷裂韌度下抽筒子的剩余壽命

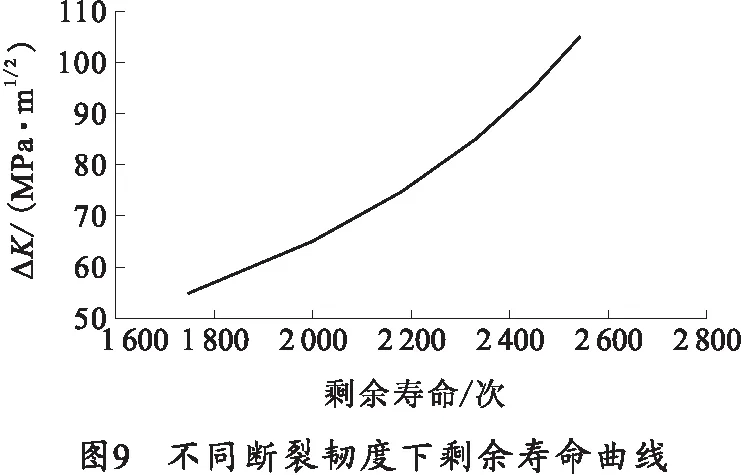
改變材料的斷裂韌度，計算可得到不同的臨界裂紋長度，通過剩余壽命預測模型得到相應的剩余壽命，如圖9所示。由圖9可知，材料的斷裂韌度越大，剩余壽命越大，且增長的趨勢越來越緩慢，可見當材料斷裂韌度越大，對剩余壽命增大的影響越來越小。

3 結論

1) 根據疲勞裂紋擴展速率實驗數據擬合出裂紋擴展速率和應力強度因子的關系曲線，進而擬合得出C和m的值，得到了45CrNiMoVA的疲勞裂紋擴展公式。

2) 設定初始裂紋長度為0.5 mm，通過材料的斷裂韌度計算可得臨界裂紋長度為3.94 mm，根據剩余壽命預測模型，估測抽筒子的剩余壽命為2 232次。

3) 通過對抽筒子剩余壽命的影響因素分析可知：當應力由300 MPa減小至200 MPa時，剩余壽命增大幅度最大，約3.2倍；應力恒定時,當初始裂紋長度從0.5 mm增大到1 mm時，剩余壽命減小幅度最大，減小約1.8倍；在合理范圍內，材料的斷裂韌度越大，剩余壽命越大，且剩余壽命增長的趨勢越來越緩慢。