考慮蠕變效應的鋼柱高溫承載力計算方法

王衛永，王芳

(1.重慶大學 土木工程學院，重慶 400045； 2.海口經濟學院 雅和人居工程學院，海口 571127)

結構的抗火性能影響結構的火災安全。火災下鋼柱的受力性能研究已積累了大量研究成果[1-5]，并寫入結構設計規范。研究發現，當溫度超過鋼材熔點的33%時，高溫蠕變對鋼構件內力和變形造成較大影響[6]。《建筑鋼結構防火技術規范》(GB 51249—2017)[7]給出的鋼柱高溫承載力計算公式沒有考慮蠕變影響。近年來，有學者重視鋼材高溫蠕變對結構抗火性能的影響，并開展了相關研究。Morovat等[8]發現鋼柱的高溫屈曲荷載與長細比、溫度以及荷載作用時間有關；恒定荷載和溫度作用下，鋼柱的撓曲位移與時間呈遞增函數關系，并定義了蠕變屈曲的概念。有學者曾采用試驗方法對鋼材的高溫蠕變性能進行了研究，發現升溫速率大于等于5 ℃/min，溫度小于等于600 ℃時，可以不單獨考慮蠕變對結構抗火性能的影響，將蠕變的影響包含在鋼材的應力-應變關系中，歐洲規范[9]中采用了該研究成果，然而，鋼材在實際火災中的升溫速率和溫度可能不在上述范圍內[10]。Wang等[11-12]通過試驗測得不同溫度和應力水平下Q345鋼和Q460鋼的蠕變變形，試驗結果對比發現，當應力較小時，第2階段蠕變對鋼構件抗火性能影響較大；擬合試驗結果得到了Norton蠕變模型參數。已有的鋼材高溫蠕變試驗結果為分析結構抗火時考慮蠕變的影響提供了重要的基礎。王衛永等[13-16]考慮蠕變后分析了鋼梁的抗火性能，并給出了考慮蠕變影響后鋼梁的承載力計算方法。王芳等[15]考慮蠕變影響后分析了Q460鋼柱的抗火性能，在分析結構變形和受力性能時引入了鋼材蠕變的影響，但沒有進一步提出考慮蠕變效應后構件高溫承載力的計算方法。

筆者采用ANSYS軟件建立鋼柱分析模型，考慮鋼材的高溫蠕變，分析鋼柱在高溫下的受力性能，通過試驗數據對模型進行了驗證，利用驗證的有限元模型進行了大量的參數分析，結果表明，考慮蠕變效應后鋼柱的高溫承載力受初始缺陷(殘余應力、初彎曲、初偏心)、彎曲方向、荷載比、長細比、升溫速率的影響較大，受截面形式和屈服強度的影響較小。在參數分析的基礎上，給出了考慮蠕變效應后鋼柱高溫承載力簡化計算方法。

1 規范計算方法

目前，歐洲和中國規范中鋼柱高溫承載力的計算公式僅考慮溫度因素，沒有考慮升溫過程，即忽略了蠕變因素的影響。

1.1 歐洲規范EC3 Part 1.2

歐洲規范EC3 Part 1.2[9]給出了鋼柱的高溫承載力計算公式

(1)

式中：N為鋼柱高溫下承載力；φT為鋼柱高溫下穩定系數；A為鋼柱的橫截面面積；fyT為鋼材高溫下屈服強度；γR為鋼柱高溫下抗力分項系數，取1.0。

鋼柱高溫下穩定性系數φT的計算公式為

(2)

(3)

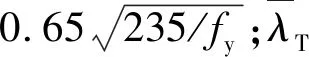
(4)

(5)

式中：λ為鋼柱長細比；λp為界限長細比；fy為鋼材常溫下屈服強度；E為鋼材常溫下彈性模量。

1.2 中國規范GB 51249—2017

《建筑鋼結構防火技術規范》(GB 51249—2017)[7]給出了鋼柱高溫下承載力計算公式。

N=φTAfyT

(6)

φT=αcφ

(7)

式中：αc為鋼柱高溫下穩定驗算參數；φ為鋼柱常溫下穩定系數，按《鋼結構設計規范》(GB 50017—2017)確定。

已有研究中很多結構抗火分析忽略了蠕變的影響，主要原因有3個：一是蠕變模型復雜且通用性差，不同的鋼材表現出不同的蠕變特性；二是結構發生火災的時間過程相對較短，認為蠕變的影響不大；三是結構抗火模擬時采用的應力-應變關系曲線包含了蠕變的影響。

2 有限元模型和試驗驗證

研究考慮蠕變的結構抗火性能時，可以采用試驗方法，也可以采用有限元模擬方法。試驗方法耗費大、周期長，數值模擬方法則靈活簡便，但模型的可靠性要經過驗證。模擬考慮蠕變的鋼結構抗火性能時，關鍵問題是蠕變模型的選擇。研究表明[17]，蠕變對結構抗火性能影響較大，且獲得鋼材高溫應力-應變關系曲線時持續時間較短，蠕變的影響不明顯，而火災溫度較高或持續時間較長時，蠕變的影響不可忽略。筆者采用基于蠕變試驗數據的蠕變模型，考慮鋼材類型的修正，系統分析了蠕變對鋼柱變形和承載力的影響。

2.1 有限元模型

采用ANSYS軟件分析考慮蠕變后鋼柱高溫下的受力性能。單元類型為SHELL181，高溫下鋼材應力-應變關系采用EC3中提供的模型，熱膨脹系數取1.2×10-5，泊松比取0.3，蠕變模型取ANSYS內置第10個蠕變方程Norton模型。

根據文獻[18]的研究成果對不同鋼材的蠕變模型進行修正，基于Wang等[11]擬合的Q345鋼材的Norton蠕變模型參數，得到

(8)

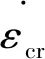
2.2 試驗驗證

LABEIN試驗室[19]對偏心距為5 mm的鋼柱進行受壓試驗和耐火試驗，試件兩端安裝刀鉸支座實現單向偏心受壓，耐火試驗采用恒載升溫的方式，試件的升溫通過電爐提供不同的升溫速率。試驗中測量了鋼柱試件的軸向變形和高度中央的水平撓度，即撓曲位移。由于升溫速率較低(5 ℃/min)，升溫時間持續較長，蠕變對試件變形的影響較大，均包含在測量的位移中。選取4根常溫試件和2根高溫試件進行有限元模型驗證。鋼柱試件的實測屈服強度fy、彈性模量E、幾何尺寸(長度L、截面高度H、截面寬度B、翼緣厚度tf、腹板厚度tw)、臨界荷載N、臨界溫度Tcr如表1所示，殘余應力分布模式如圖1(殘余應力幅值a=0.1)所示。

表1 試驗試件的參數Table 1 Parameters of the experimental tests

圖1 殘余應力分布模式Fig.1 Distribution of residual

有限元分析得到常溫試件(AL1、AL3、SL43和AL6)的荷載-位移曲線，與試驗結果進行對比如圖2所示。對比發現，有限元分析得到柱的高度中央側向位移的變化趨勢與試驗一致，臨界荷載基本重合，證明了有限元模型的可靠性。

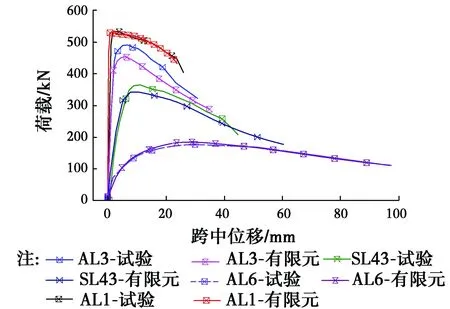
圖2 有限元與試驗結果對比Fig.2 Comparison between FEA and test

利用驗證過的有限元模型對高溫試件(CL1和DL6)進行模擬，進而分析蠕變對鋼柱高溫下承載力的影響。試驗中試件的加熱速率為5 ℃/min，實測最大溫差小于100 ℃，表明試件沿截面和長度方向的溫度分布基本均勻。為了簡化分析，有限元模型中試件的溫度采用平均溫度。高溫蠕變對試件CL1和DL6軸向位移和撓曲位移的影響如圖3、圖4所示。對比發現，相對不考慮蠕變效應的鋼柱，考慮蠕變效應后鋼柱提前進入彈塑性階段；進入彈塑性階段后，考慮蠕變效應后鋼柱的軸向位移和側向位移變化速率較快，表明蠕變影響鋼柱的抗火性能；考慮蠕變效應后鋼柱的軸向位移和撓曲位移與試驗結果更吻合，表明有限元模型中考慮蠕變效應后能更準確地預測鋼柱的耐火性能。這是因為蠕變在一定的應力水平和溫度下，會導致結構的變形隨時間而增大，有限元分析時若忽略蠕變變形的影響，計算出的結構變形相對較小，而結構變形又會影響結構的承載力，對于鋼柱而言，撓曲變形增大時二階效應會變得更加明顯，從而導致耐火極限降低。因此，不考慮蠕變的有限元分析得到的耐火極限結果偏大。

圖3 試件CL1位移比較Fig.3 Comparison of displacement for specimen

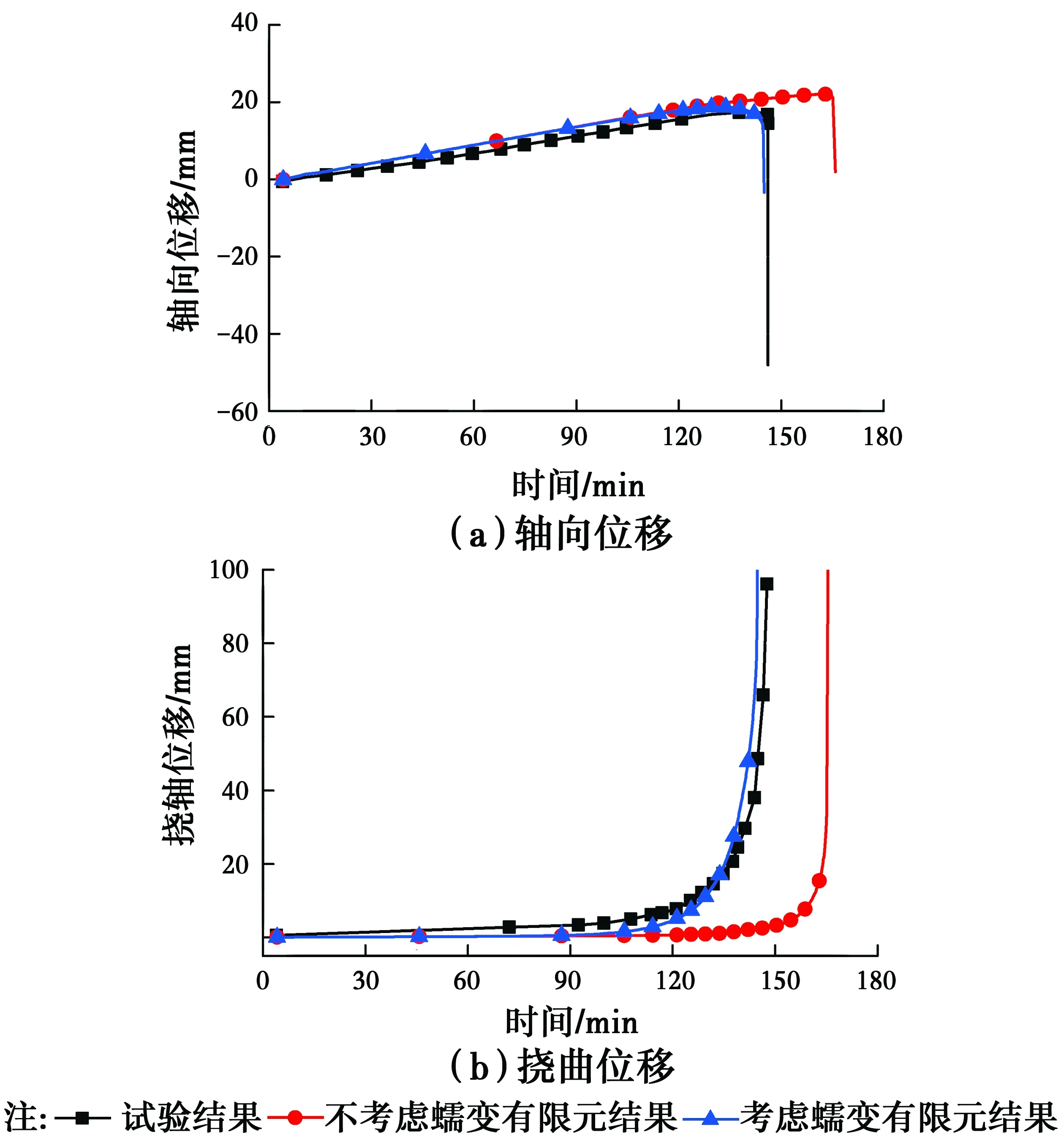
圖4 試件DL6位移比較Fig.4 Comparison of displacement for specimen

3 參數分析

利用驗證的有限元模型，分析考慮蠕變效應后鋼柱在不同殘余應力、初彎曲、初偏心、彎曲方向、截面形式、屈服強度下的耐火性能，進而得到考慮蠕變效應后影響鋼柱承載力的主要參數。

3.1 殘余應力

圖5 殘余應力的影響

從圖5(a)可以看出，不同殘余應力幅值下臨界溫度隨長細比變化趨勢相似，臨界溫度隨著長細比的增加而降低；相同長細比下，臨界溫度隨殘余應力幅值的提高而降低。從圖5(b)可以看出，不同殘余應力幅值下高溫穩定系數隨長細比變化趨勢也相似，高溫穩定系數隨著長細比的增加而降低；相同長細比下，高溫穩定數隨殘余應力幅值的增加而降低。對長細比較大的鋼柱，殘余應力對鋼柱的臨界溫度影響較大，以長細比為100的鋼柱為例，殘余應力幅值為0.5的鋼柱比0.1的鋼柱臨界溫度低40 ℃左右。

3.2 初彎曲

圖6 初彎曲的影響

從圖6(a)可以看出，不同初彎曲下臨界溫度隨長細比變化趨勢基本相同，臨界溫度隨長細比增加而降低；相同長細比下，臨界溫度隨初彎曲的增加而降低。從圖6(b)可以得到，不同初彎曲下高溫穩定系數隨長細比的增加而降低；相同長細比下，高溫穩定系數隨初彎曲的增加而降低。初彎曲對臨界溫度的影響較大，以長細比為80的鋼柱為例，初彎曲為1‰鋼柱的臨界溫度比無初彎曲的鋼柱低40 ℃左右。

3.3 荷載初偏心

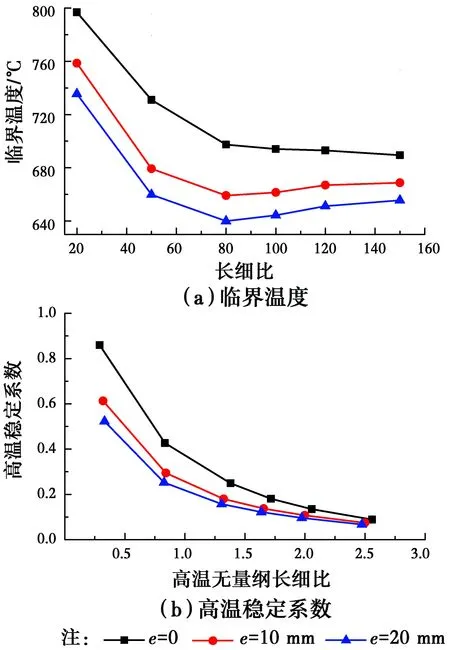
圖7 荷載初偏心的影響Fig.7 Effect of load initial

從圖7(a)可以看出，初偏心對臨界溫度的影響較大；相同長細比下，初偏心越大，臨界溫度越低。以長細比為80的鋼柱為例，初偏心為20 mm鋼柱的臨界溫度比無初偏心的鋼柱低60 ℃左右。當長細比大于80時，臨界溫度隨長細比的增加而提高，造成這種現象的原因是鋼柱較長時初偏心大的構件為壓彎構件，其臨界溫度的計算方法與軸心受力構件不同。從圖7(b)可以看出，初偏心對高溫穩定系影響很大，尤其是對長細比小的鋼柱影響更大，隨著初偏心的提高，高溫穩定系數降低。

3.4 彎曲方向

圖8 彎曲方向的影響

從圖8(a)可以看出，相同長細比下，繞弱軸彎曲鋼柱的臨界溫度小于繞強軸彎曲的臨界溫度，長細比越大，兩者結果相差越大；繞弱軸彎曲時，臨界溫度隨長細比的增大而減小，而繞強軸彎曲時，臨界溫度隨長細比的增大先減小后增大。產生這種現象的原因是，計算臨界溫度時采用的是相同的荷載比，隨長細比的增大，鋼柱的承載力降低，其承受的荷載也降低，從而可能造成臨界溫度的提高。另外，對于焊接H形截面，殘余應力對鋼柱繞強軸彎曲時影響小一些，造成臨界溫度高。從圖8(b)可以看出，不同彎曲方向下鋼柱的高溫穩定系數隨長細比變化趨勢相同，長細比越大，高溫穩定系數越低；相同長細比下，繞強軸彎曲的高溫穩定系數大于繞弱軸彎曲的高溫穩定系數，長細比越大，兩者結果相差越大。

3.5 截面形式

圖9 截面形式的影響

從圖9(a)可以看出，不同截面形式鋼柱的臨界溫度隨長細比的變化趨勢相同；相同長細比下，3種截面形式的臨界溫度相差較小，因此，截面形式基本不影響鋼柱的臨界溫度。從圖9(b)可以看出，不同截面形式下鋼柱的高溫穩定系數隨長細比的變化趨勢也相同，高溫穩定系數隨長細比增加而降低；相同長細比下，3種截面形式的高溫穩定系數相差較小，也可以看出截面形式對鋼柱的高溫穩定系數影響很小。

3.6 屈服強度

圖10 屈服強度的影響

從圖10(a)可以看出，相同屈服強度下，不同荷載比的臨界溫度隨長細比的變化趨勢相同；相同荷載比和長細比下，3個屈服強度的臨界溫度相差較小，因此，屈服強度對鋼柱的臨界溫度影響較小；相同長細比下，荷載比越大，臨界溫度越小。從圖10(b)可知，不同荷載比下鋼柱的高溫穩定系數隨長細比的變化趨勢基本相同，高溫穩定系數隨長細比增加而降低；相同荷載比下，3種屈服強度的高溫穩定系數——高溫無量綱長細比曲線相差較小，因此，屈服強度對鋼柱的高溫穩定系數影響很小。

4 計算方法

中國現行《鋼結構設計規范》(GB 50017—2017)中，鋼柱的臨界應力表達式是利用數值方法擬合而成的Perry公式，進而反算出考慮初彎曲、殘余應力、截面形式、彎曲方向和長細比的等效初偏心率e0[20]。可參照上述常溫下鋼柱臨界應力的計算方法得到考慮高溫蠕變效應后鋼柱的臨界應力。

4.1 無初始缺陷

圖11 不考慮初始缺陷的鋼柱高溫穩定系數Fig.11 Stability coefficient of steel column

從圖11容易發現，長細比和升溫速率是影響鋼柱高溫穩定系數的主要參數，荷載比是次要參數；無初始缺陷下，鋼柱的高溫穩定系數與長細比呈遞減關系；相同長細比下，鋼柱的高溫穩定系數明顯低于歐拉公式的計算結果，兩者差值隨長細比的減小而增大，這是由于歐拉公式僅適用于細長桿；蠕變影響下中長柱的臨界溫度相差較大，造成中長柱的高溫穩定系數分布較為離散；繞弱軸彎曲的高溫穩定系數比繞強軸彎曲的高溫穩定系數小。

4.2 有初始缺陷

圖12 考慮初始缺陷的鋼柱高溫穩定系數Fig.12 Stability coefficient of steel column

從圖12中可以看出，考慮蠕變效應的高溫穩定系數明顯小于規范的計算結果。因此，忽略蠕變后，規范中高溫下鋼柱的承載力計算結果偏于不安全。

4.3 公式推導

高溫下鋼材在任意時刻t的總應變

εt=εth,t(T)+εσ,t(σ,T)+εcr,t(σ,T,t)

(9)

式中：εth,t、εσ,t、εcr,t分別為熱膨脹應變、瞬時應變和蠕變應變。

式(8)推導得蠕變應變增量

Δεcr=c1σc2e-c3/T·Δt， Δt→0

(10)

將式(10)代入式(8)得到任意時刻t不考慮初始缺陷的蠕變應變

(11)

任意時刻t的瞬時應變

(12)

式(11)、(12)代入式(9)，得

(13)

式(13)兩邊同時對εt求偏導，得

(14)

整理式(14)得考慮蠕變影響的切線模量

(15)

由切線模量理論得考慮蠕變影響的屈曲荷載

Pt=

(16)

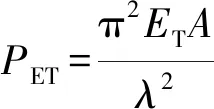
整理式(16)，得

(17)

(18)

令

(19)

忽略δ的高階(二階以上)無窮小，則有

(20)

將式(19)、(20)代入式(18)，令δ相同次冪的系數為0，則有

(21)

(22)

依次求解上述方程得

(23)

(24)

將式(23)、(24)代入式(19)得

(25)

式中：

(26)

(27)

由圖11可知，當λ<λp時，蠕變對鋼柱抗火性能的影響較小。利用圖11的參數分析結果對式(25)進行修正，得到不考慮初始缺陷下軸壓構件(λ≥λp)的屈曲應力

(28)

式中：

(29)

(30)

(31)

(32)

利用式(28)、圖12的參數分析結果和Perry公式，反算出等效初偏心率，得到考慮蠕變影響的軸壓構件(λ≥λp)的臨界應力

(33)

式中：

(34)

(35)

(36)

4.4 算例驗證

圖13對比了考慮蠕變后鋼柱的簡化計算結果和有限元分析結果，發現兩者誤差均在±5%左右，驗證了上述考慮蠕變效應后鋼柱臨界應力計算方法的準確性。

圖13 簡化計算與有限元分析的結果對比Fig.13 Comparison of results between simplified calculation and finite element

5 結論

利用經驗證的有限元模型分析了考慮蠕變效應后多個參數對鋼柱抗火性能的影響。得到以下主要結論：

1)初始缺陷(殘余應力、初彎曲、初偏心)、彎曲方向、荷載比、長細比、升溫速率對鋼柱的高溫承載力影響較大。

2)截面形式和屈服強度對鋼柱的高溫承載力影響較小。

3)給出了鋼柱高溫承載力的簡化計算方法，可用于考慮蠕變影響的鋼柱高溫承載力預測。