三條線段間數量關系的方法探討
吳慧琳
(江蘇省揚州市竹西中學 225000)
三條線段間數量關系的探討是猜想證明題型的應用典范.一般無法通過一次性的操作解決,而要通過巧妙的方法加以轉化.學生解決此類題型時,常找不到突破口,教師講解時,應引導學生分析探討的過程,使學生不僅知其然,還要能知所以然,以達到“授之以漁”的目的.下面結合具體事例談談三條線段間的數量關系探討的研究方法和途徑.
一、等積法得數量關系
例1在△ABC中,AB=AC,P底邊BC上一點,PD⊥AB于D,PE⊥AC于E,CF⊥AB于F.探索PD、PE、CF三者的數量關系.
解連接AP.∵S△ABC=S△ABP+S△ACP,
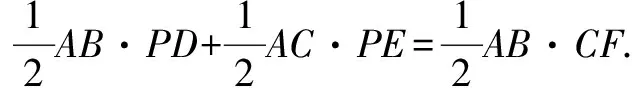
∵AB=AC,
∴PD+PE=CF.
二、相似法得數量關系
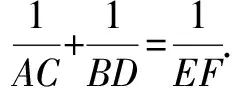
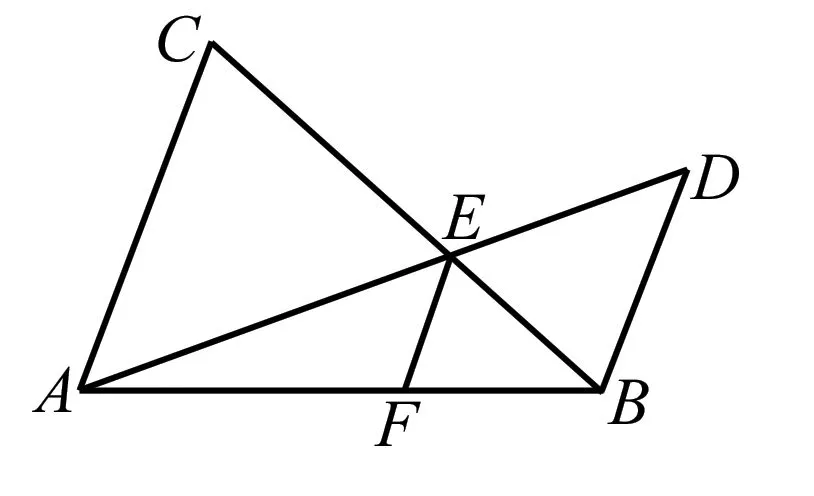
證明∵EF∥BD,
∴△AEF∽△ADB,
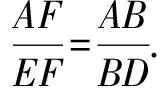
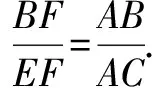
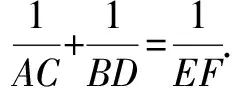
三、旋轉法得數量關系
例3如圖,在同一平面內,將兩個全等的等腰直角三角形ABC和AFG擺放在一起,A為公共頂點,∠BAC=∠AGF=90°,若△ABC固定不動,△AFG繞點A旋轉,AF、AG與BC的交點分別為D、E(點D不與點B重合,點E不與點C重合),在旋轉過程中,探索BD、CE、DE三條線段之間的數量關系.
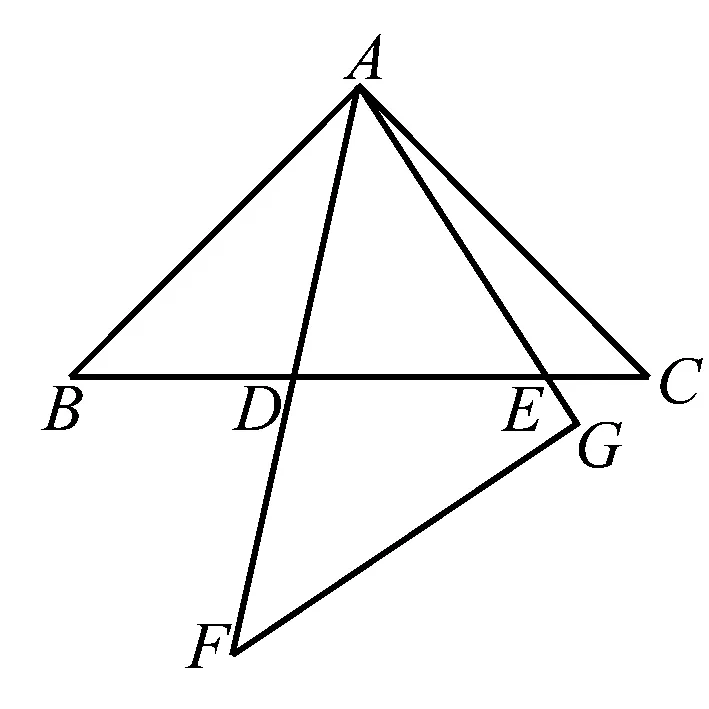
解將△ACE繞點A順時針旋轉90°至△ABH的位置,則CE=HB,AE=AH,∠ABH=∠C=45°,旋轉角∠EAH=90°.連接HD,在△EAD和△HAD中,∵AE=AH,∠HAD=∠EAH-∠FAG=45°=∠EAD,AD=AD,∴△EAD≌△HAD,∴DH=DE.又∠HBD=∠ABH+∠ABD=90°,∴BD2+HB2=DH2,即BD2+CE2=DE2.
四、補短法得數量關系
例4如圖,正方形ABCD中,∠EDF=45°,且∠EDF的兩邊分別與AB,BC交于E,F. 試探究AE,EF,CF三條線段之間的數量關系,并證明你的結論.
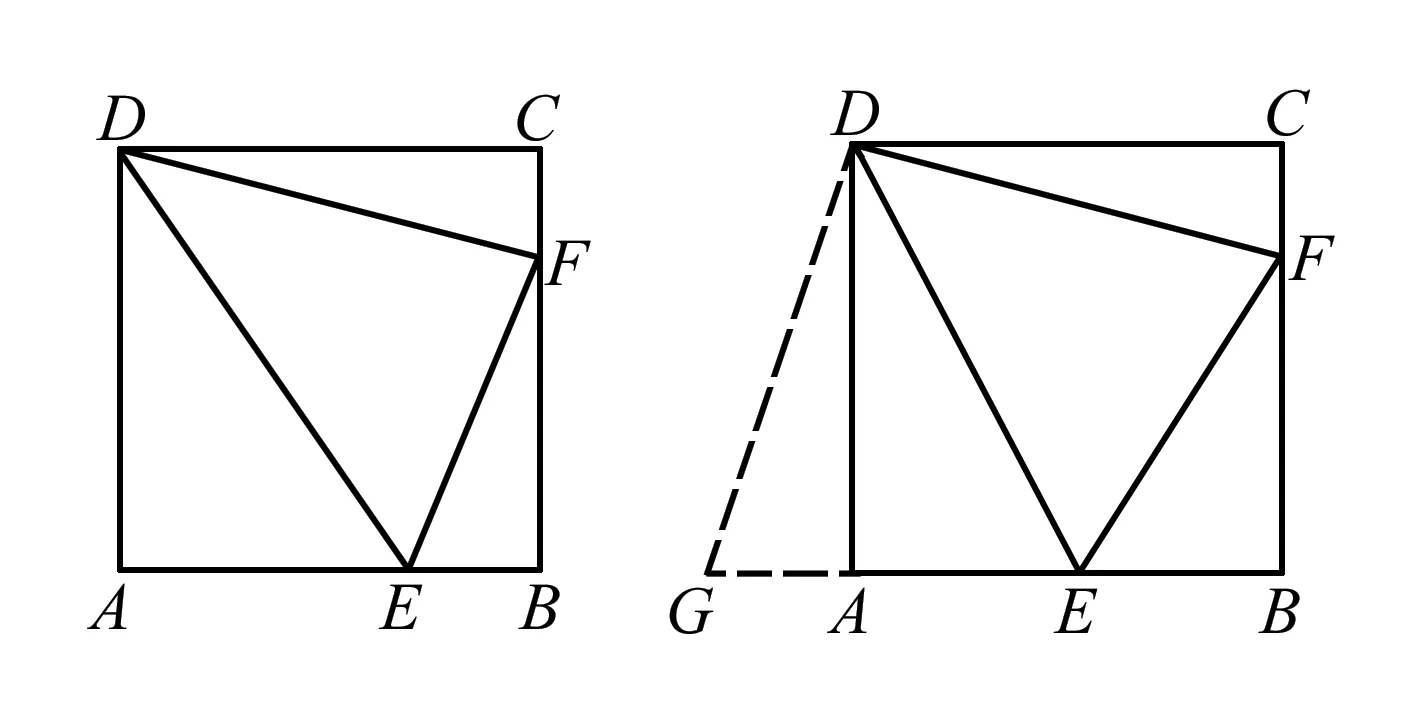
解EF=AE+FC.理由:如圖所示:延長BA至G,使AG=CF,連接DG.
∵在△ADG和△CDF中,AD=CD∠DAG=∠C=90°,AG=CF,∴△ADG≌△CDF(SAS),
∴DG=DF,∠ADG=∠CDF.又∵∠EDF=45°,∠ADC=90°,∴∠DAE+∠CDF=∠ADG+∠DAE=∠GDE=45°,∴∠GDE=∠EDF.在△DGE和△DFE中,DG=DF,∠GDE=∠EDF,DE=DE,∴△DGE≌△DFE(SAS),∴GE=EF.又∵AG=CF,∴EF=AE+FC.
五、截長法得數量關系
例5已知:如圖,△ABC中,∠C=2∠B,∠1=∠2,求證:AB=AC+CD.
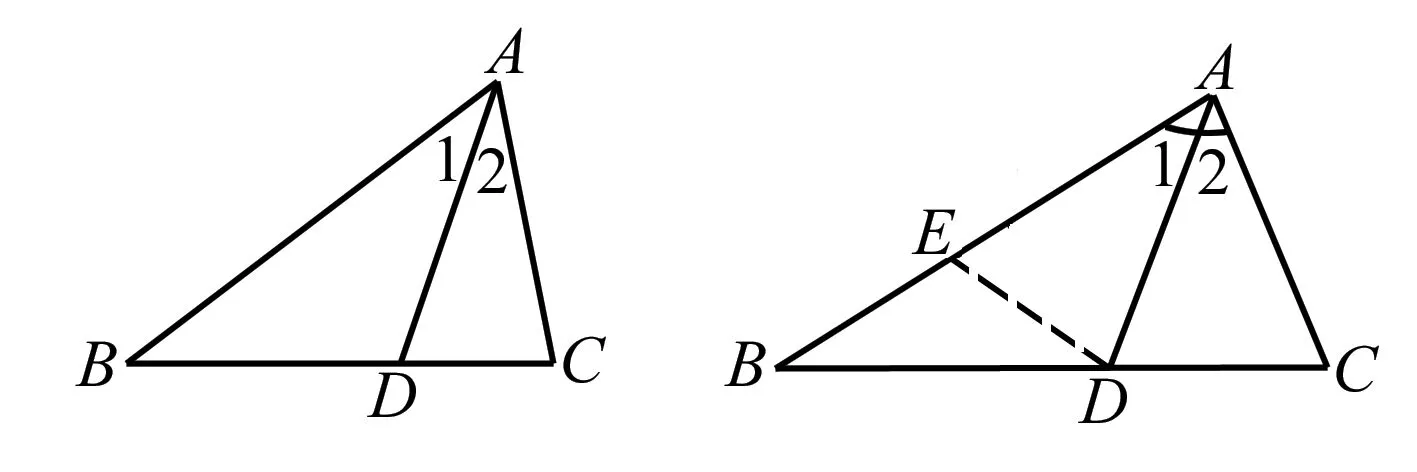
證明在AB上取AE=AC,連接DE,∵AE=AC,∠1=∠2,且AD=AD,∴△ACD≌△AED(SAS),∴ED=CD,∠AED=∠C=2∠B,又∵∠AED=∠B+∠BDE,∴∠B=∠BDE,∴EB=ED,即△BED為等腰三角形.∴BE=ED=CD,∴AB=AE+EB=AC+CD.
六、構造法得數量關系
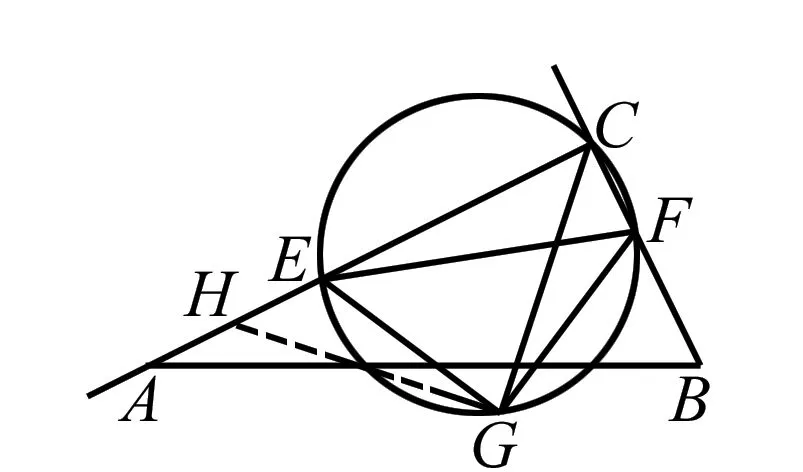

證明當0 ∵∠ECG=45°,∴∠EHG=45°,∴∠EHG=∠FCG. 在△EGH和△FGC中,∠EGH=∠FGC,BE=FG,∠CHG=∠GCF,∴△EGH≌△FGC.∴EH=FC. 本題也可進行拓展:當t≥4時,CE、CF、CG的數量關系是否發生變化,并說明理由. 通過上述的幾種方法可知,探討三條線段間的數量關系,需認真分析題目中的已知條件,巧添、巧截、巧補、巧轉,尋求解決問題的最佳途徑,掌握住方法,就能做到會一題,通一類,知一片,使得復習效果事半功倍.