基于MRF和水平集的圖像分割方法

劉旋

(信陽農林學院 財務處，河南 信陽 464000 )

1 引言

圖像分割是數字圖像處理的一個重要領域，近年來作為圖像識別和計算機視覺的基礎研究課題受到廣大學者的關注。Osher[1]等人自1988年提出了水平集方法以來，曲線演化的形變模型被廣泛地應用于圖像數字處理等領域。2001年Chan[2]等人提出了CV模型(Chan-Vese Model)，不僅抗噪聲能力顯著提高,而且對邊緣模糊的圖像目標有較好的分割結果。李傳明[3]等人提出了一種基于區域的水平集圖像分割方法，能夠較好地處理圖像介質不均勻性問題，并成功應用于醫學圖像分割。唐利明[4]等人在2014年提出了基于變分水平集的圖像模糊聚類分割，該算法對噪聲圖像的聚類分割魯棒性更強。

現有方法在計算圖像信息時，首先假設各區域內像素是獨立分布的，因此導致在處理含有大量噪聲的圖像時，容易受到噪聲點的干擾，得到不理想的分割結果。雖然眾多改進的水平集方法在很多圖像上體現出了良好的性能，能夠有效地克服噪聲帶來的影響，但對于一些較為復雜的圖像來說，比如目標被遮擋或缺損，目標與背景的灰度非常接近等情況，如果沒有形狀先驗信息的支持和初始輪廓的選擇，分割結果將很難令人滿意。

根據上述問題，本文提出了一種基于局部鄰域信息的水平集方法。該算法首先用K-means聚類獲得圖像先驗信息和初始演化曲線，然后結合MRF方法得到局部鄰域能量信息，加入水平集方法中。該模型可以在較少的迭代次數中分割含大量噪聲的圖像，并獲得較為理想的結果。此外在能量泛函中加入能量懲罰項可以避免較為耗時的重新初始化步驟，使得相應的計算時間大為減少。

2 MRF和水平集理論

2.1 MRF-MAP理論

馬爾科夫隨機場(MRF)[5]能夠將圖像分割轉化為對像素的標記，將圖像分割轉化為對像素的分類，其后驗概率最大估計(MAP)的數學模型為：

P(ω/F)=P(ω)P(F/ω)/P(F)

(1)

其中,P(F)觀測圖像F的概率分布，P(ω)是圖像數據標簽場ω的先驗概率。P(F/ ω)是觀測場F對于標記場ω的條件概率，其概率函數是符合高斯分布。

(2)

這里,S為圖像分割的種類，而μs為標號是s類像素的均值，σS代表s類的方差。當標簽場的最大后驗概率P(ω/F)達到最大值時，即所有像素都得到最合適的歸類。因為觀測圖像F是已知的，所以P(F)是一個常量，根據文獻[4]的證明，可求得P(ω)的概率密度函數如下:

(3)

(4)

這里Z是歸一化的常數，參數T控制概率分布P(ω)的形狀，C為所有雙點勢團的集合，Vc(ωc)為勢團勢能，本文選取ISING 模型，其中β是耦合系數，它的取值一般為2。其中像素點r為像素點s鄰域內的點，這里采用8鄰域系統，圖像中的每一個像素點與其相鄰的雙點勢團有8個，所以標簽場的最大后驗概率計算如下：

(5)

2.2 水平集理論

水平集方法利用零水平集將運動界面嵌入到更高維的水平集函數中，由閉超曲面的演化方程得到水平集函數的演化方程，進而實現圖像目標的輪廓提取[6]。假設二維平面上的曲線由y = f(x)表示，那么可以定義曲面方程為φ(x,y) = y-f(x)，則φ(x,y) = 0就是曲線的隱式表達，即用三維空間中的曲面來隱式表達二維平面上的曲線。

在眾多的水平集方法中，Chan-Vese模型利用曲線的內外灰度均值來促進水平集的演化，在分割梯度無用或邊緣模糊的圖像上取得了較好的分割效果。該模型不僅能夠檢測內部輪廓，并且對于噪聲不敏感，其主要通過最小化公式(6)的能量泛函來實現：

(6)

其中a，λ1和λ2是常數，一般情況下可固定λ1=λ2=1, μ1和μ2分別是演化曲線φ內部和外部的像素灰度均值。L(φ)是某種外部能量泛函，用來驅使零水平集向著圖像中的目標邊界運動，該項與演化曲線的長度有關。

為了求解能量E(μ1, μ2,φ)的最小值，Chan-Vese算法采用水平集的思想，用水平集函數φ(x,y)表示演化曲線。若像素點(x,y)在φ的輪廓內，則φ(x,y) > 0；若像素點(x,y)在φ的輪廓外時，則φ(x,y) < 0;而當像素點(x,y)剛好在φ輪廓邊界上時，則φ(x,y) = 0。通過曲線φ的不斷演化，最后求得穩定的最小能量泛函。

3 基于MRF的水平集算法

上述的CV模型也存在著一些問題：(1)不能分割具有灰度不均勻性質的圖像；(2)對初始輪廓的設置有一定的依賴性，重新初始化問題。而MRF模型自身沒有任何分割能力，需將其嵌入到具體的圖像分割算法中去，以達到分割的目的。

對于先驗概率P(ω)，本文采用K-means聚類[7]進行求解，使得隸屬度函數的分布更加合理，時間復雜度更低，并為CV模型提供優化后的先驗信息。K-means聚類是一種快速且高效的聚類方法，可以從圖像中計算盡可能多的原始信息。傳統的水平集方法中沒有考慮鄰域信息，對噪聲和圖像灰度不均非常敏感,而MRF融合了像素的鄰域信息，使周圍像素也能落入正確的分類中，克服了該算法的弊端，可以獲得更理想的分割結果。本文定義新的能量泛函為E(φ):

E(φ)=α·P(φ)+β·L(φ)+EMRF

(7)

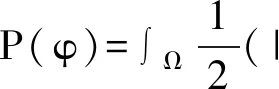
(8)

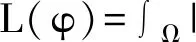
(9)

(10)

其中，α和β為常數，H(φ)是海氏函數的正則化形式。P(φ)是水平集函數φ的內部能量泛函，代表水平集函數偏離符號距離函數的程度，用來糾正水平集函數與符號距離函數的差[8]。L(φ)為外部能量泛函,用來驅使零水平集向目標邊界演化運動[9]。EMRF加入像素的鄰域信息到能力泛函中，負責將演化曲線C吸引到目標輪廓上來。EMRF用最大后驗概率(MAP)求解，最后根據公式(5)計算MRF泛函的目標能量P(O/F)和背景能量P(B/F)組成：

其中，λ1和λ2是取值為正的常數，O代表曲線內目標圖像，B代表曲線外背景圖像，通過計算上述能量泛函E(φ)，最終求得穩定的目標輪廓曲線，本文算法的具體流程如下：

Step1：初始化零水平集曲線φ，使用K-means聚類獲取初始分割的圖像標號場P(F)。

Step2：分別計算演化曲線內部和外部的均值μ1, μ2,、方差σ1,σ2，然后根據公式(5)求得曲線內外的先驗概率P(O/F)和P(B/F)，最后根據式(11)計算EMRF能量泛函。

Step3：利用式(8)和式(9)計算圖像內部能量泛函P(φ)和L(φ)，然后根據公式(7)求得總能量泛函E(φ)。

Step4：重復步驟1-3，不斷演化零水平集方程，經過迭代求得E(φ)n到E(φ)n+1，當滿足|E(φ)n+1-E(φ)n|>T時(T為演化閾值)，退出循環；否則繼續。

Step5：根據得到的目標輪廓曲線，提取最終的分割結果。

4 實驗結果與分析

本文首先選取若干目標模糊的醫學圖像(血管、細胞)進行實驗。通過與文獻[9]算法、LBF算法[10]、LIF算法[11]進行實驗對比，圖1(a)為包含血管和細胞的原始醫學灰度圖像，文獻[9]、LBF算法、LIF算法和本文算法的分割結果分別如圖1(b)、圖1(c)、圖1(d)和圖1(e)所示。本文的參數選值為：α=β=λ1=λ2=1,T=0.001。

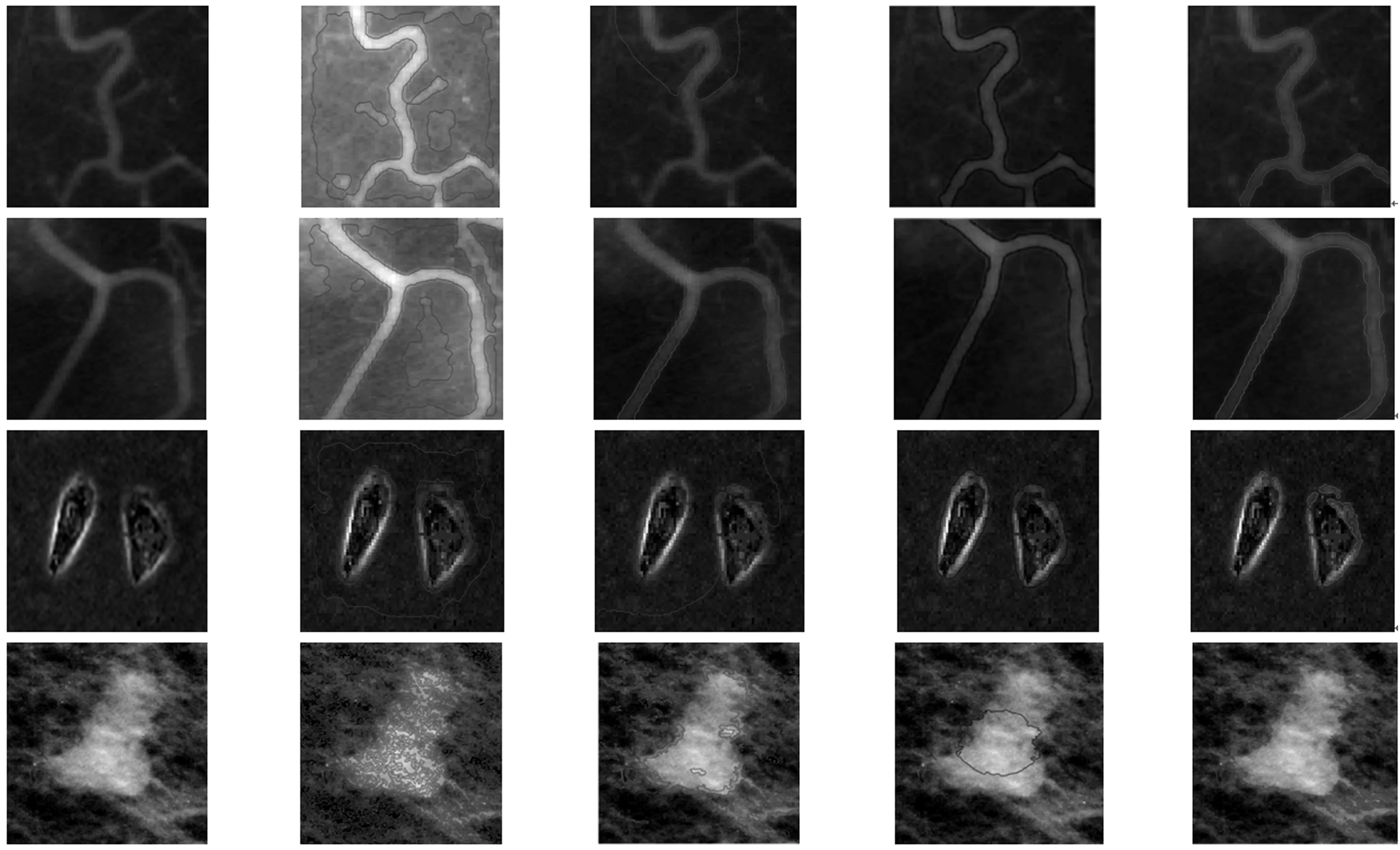
(a)原始圖像 (b)文獻[9]算法 (c)LBF方法 (d)LIF方法 (e)本文方法

圖1醫學圖像分割結果

文獻[9]算法雖然無需初始化曲線，就能清晰地提取目標物體的弱邊界，但是在處理前景模糊的醫學圖像時，難以演化到正確的邊界，如圖1(b)中得圖像目標邊界均沒有被正確提取。LBF算法可以較準確地捕捉圖像的邊界信息，但分割結果依賴于初始輪廓曲線的選擇，如圖1(c)中的第2幅圖像能夠得到正確的分割，但是其他圖像的分割結果受到初始曲線的影響而不理想。LIF方法能夠很好地分割模糊弱邊界圖像，且不受初始曲線選擇的影響，但是當圖像含有大量噪聲時，曲線就難以演化，如圖1(d)前三幅圖像均能得到較好的分割結果，但是最后一幅圖像包含噪聲較多，零水平集曲線難以演化。而本文方法能夠克服圖像中的噪聲，實現自適應演化，不依賴初始輪廓，對弱邊界的分割更加準確平滑，與以上方法相比，本文的分割結果更加清晰準確，且抗噪性更好。

為了進一步驗證本文改進方法的有效性，本文與文獻[4]一種基于變分水平集的模糊聚類算法進行對比，該算法在噪聲圖像的處理上效果良好。通過選取三幅含有大量噪聲的圖像進行實驗，圖2(a)為包含椒鹽噪聲(δ= 40)的原始圖像，文獻[4]算法、本文算法的分割結果分別如圖2(b)和圖2(c)所示。從圖2的分割結果可以發現，本文算法在保證抗噪性能的同時，能夠得到更平滑、準確的分割輪廓，例如文獻[4]算法將飛機圖像的陰影也分割為目標圖像，而對第三幅遙感圖像灰度不均勻的地質信息也沒有準確提取，所以，本文算法的魯棒性更好。

(a)原始圖像 (b)文獻[4]算法 (c)本文方法

圖2噪聲圖像分割結果

5 結論

圖像分割的自適應提取和抗噪聲一直是一個難題，本文通過對水平集算法的改進，提出了一種基于MRF的水平集分割方法，有效地解決了目標模糊、包含大量噪聲的圖像信息提取。通過與一些水平集方法的對比實驗進一步說明了本文方法對噪聲圖像分割的有效性。而對于多目標噪聲圖像的分割，如何綜合多個粒度進行演化分析，將EM-GMM(高斯混合模型)方法納入MRF能量函數[12]中產生多個粒度下的分割結果，是一個值得深入研究的課題。