微元法在高中物理中的妙用

于潤鵬

(山東省聊城市茌平縣第一中學 252100)

一、什么是微元法

“微元”思想在我國最早出自莊子《天下篇》：“一尺之錘，日取其半，萬世不竭”，但直到牛頓時期，這一方法才被廣泛應用，成為分析解決數學和物理問題的常用方法.

微元法就是將復雜的物理過程分成眾多微小的“元過程”，然后對“元過程”進行分析，找出其物理規律，再將此規律通過一定的數學方法或物理思想運用到整個過程，從而解決問題.選取的“元”代表了整個物理過程的基本特征，例如可以選取一段時間——時間元，一部分面積——面積元，一段圓弧——線元，一部分質量——質量元等等.

二、列舉：人教版高中物理教科書中的微元思想

高中學生數學知識有限，當面對一些需要使用微分、積分來分析的復雜物理問題，往往難以理解，借助微元思想可以化難為易，從而幫助學生解決認知和思維上的困難.具體方法就是先對具有代表性的“元過程”進行物理分析，再利用數學方法將“元過程”推廣到整個物理過程.下面就以人教版高中物理教材為例，列舉應用微元思想的幾個知識點：

人教版高中物理教科書中微元思想舉例.

知識點微元元素主要內容瞬時速度的定義時間元Δt取Δt足夠小,對平均速度的元過程求極限用打點計時器測量瞬時速度時間元Δt取Δt足夠小,算出平均速度代替瞬時速度勻變速直線運動的位移面積元Δs在v-t圖像上,物體的位移可看做無數個微小的Δs疊加,即梯形的面積重力勢能:重力做的功高度元Δh將任意路徑分成眾多小間隔,每個小間隔可近似成一條傾斜的直線,每段高度差為Δh,疊加后即為重力在整個路徑上所做的功探究彈性勢能的表達式:拉力做的功長度元ΔL彈簧拉伸的過程分成多個小段,將每小段ΔL上的力視為恒力,將各小段上拉力做的功疊加

三、列舉：微元法在高考試題和物理競賽中的妙用

物理教材中的眾多內容中滲透的微元思想，為學生解決物理問題提供了全新的視角和巧妙的途徑.采用微元法可以將復雜、動態的物理問題簡單化，具體解題方法可以概括為①無限分割：取元②尋找“元”規律③逼近：積分疊加.

例如：半徑為R的半球形容器裝滿密度為ρ的液體.要將容器內的液體全部抽出,至少需要做多少功?用含ρ，R，π的式子表示.

解析將容器內的液體全部抽出需最少功即將所有液體抽到球心高度所需功的和.利用微元法解題如下：

1.無限分割：取“元”

如圖2所示在距球心x處，取一高度為dx的液體.

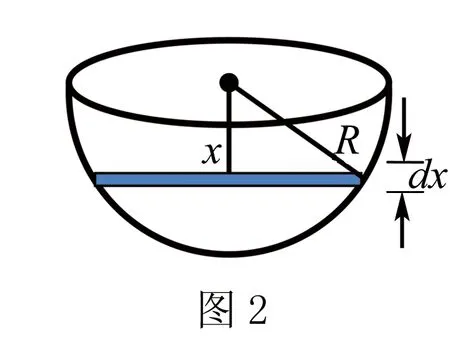
2.尋找“元”規律

距球心x到x+dx處的液體體積為π×(R2-x2)×dx

將這些液體抽到球心至少做功為

W=ρgπx(R2-x2)dx

3.逼近：積分疊加

將所有功積分(從0積到R)

dW=ρgπx(R2-x2)dx

評析本題的難點是：每一部分液體被抽出的高度不同，無法利用公式求得所做的功.采取分割取元的方法，將一小段液柱為研究對象，再結合微元的物理意義，得到對微元內水柱做功的大小，之后運用數學工具再對整體疊加積分從而突破難點.

綜上可見，微元法的本質是通過化靜為動、化曲為直、化變為恒等方式，將物理模型巧妙的轉化為數學問題，通過對“微元”累計疊加后再回歸物理情境.這種從片斷到整體的思維方式，為分析解決高中物理力學、電磁學中一些復雜的問題中提供了全新的思路，也為大學微積分的學習奠定了良好的基礎，促進了學生的物理建模能力和數學思維能力的發展，極大提升了學生的科學素養.