纖維分布與界面強度對復合材料橫向壓縮性能影響分析
萬小朋, 楊光猛, 趙美英
(西北工業大學 航空學院, 陜西 西安 710072)
纖維增強復合材料具有比強度高、比剛度大、可設計強以及良好的抗疲勞性能等優點,在航空航天等眾多領域得到廣泛應用。然而復合材料復雜的損傷失效過程以及破壞模式給力學性能仿真分析以及結構應用帶來巨大的難度[1-2]。
近年來基于代表性體積單元(representative volume element,RVE)的微觀力學損傷模型在預測復合材料損傷過程和強度性能中得到廣泛應用[3-5]。微觀力學模型中對纖維分布形貌以及組分材料本構關系的準確描述是預測單向復合材料力學性能的關鍵。González等[6]對比了6組纖維隨機分布模型仿真得到的復合材料橫向壓縮應力-應變曲線,結果表明纖維分布形式對損傷后的應力-應變曲線變化有一定影響。Totry等[7-8]進一步研究表明不同隨機分布形式在預測復合材料C/epoxy和C/peek橫向壓縮強度的偏差分別為3%和7%。上述研究表明纖維分布形式會對單向復合材料力學性能的預測精度產生影響,需要在數值分析中加以考慮。
組分材料性能參數是影響單向復合材料力學性能的一個重要因素。一般來說組分材料中纖維與基體的性能可以通過強度試驗獲得,然而界面強度很難通過傳統試驗方法獲得,并且對于同一材料,界面脫黏起始點判定、試驗方法以及試樣幾何差異等因素的不同,同樣會導致測出的數據分散性很大[9]。當前數值分析中界面強度的選取主要有3種方案:①采用Mohr-Coulomb(M-C)彈塑性準則對基體力學行為進行描述時,選取M-C準則中基體的黏聚力作為界面強度[6,10-11];②采用基體強度作為界面強度[12];③通過分析界面強度對仿真結果的影響規律,反演出與試驗結果較為吻合的界面參數值[5,13]。然而3種方案中方案①和方案②只對于特定材料性能的仿真具有很好的精度,方案③需要進行復合材料力學性能試驗,花費較高且時間歷程過長。
基于上述原因,本文通過C++編寫纖維隨機分布算法,使用python在Abaqus中參數化生成包含纖維、基體和界面的復合材料代表性體積單元模型,采用擴展的線性Drucker-Prager(D-P)彈塑性準則[14]和雙線性內聚力模型分別描述基體和界面的本構關系,最終建立了復合材料二維損傷微觀力學模型。在此基礎上研究分析纖維分布形式與界面強度對單向復合材料橫向壓縮強度的影響。
1 微觀力學數值分析模型
1.1 微觀結構中纖維分布的生成
在單向復合材料固化過程中,纖維單絲浸潤在流動性樹脂中,鋪設出的單向層纖維呈隨機分布。為了研究纖維隨機分布對單向層力學性能的影響,采用隨機擴張算法[15]生成纖維隨機分布模型,生成步驟如下所示:
1) 輸入纖維體積含量和纖維半徑,計算出目標區域尺寸;
2) 利用隨機函數生成第一根纖維的圓心坐標(x1,y1),設為當前纖維;
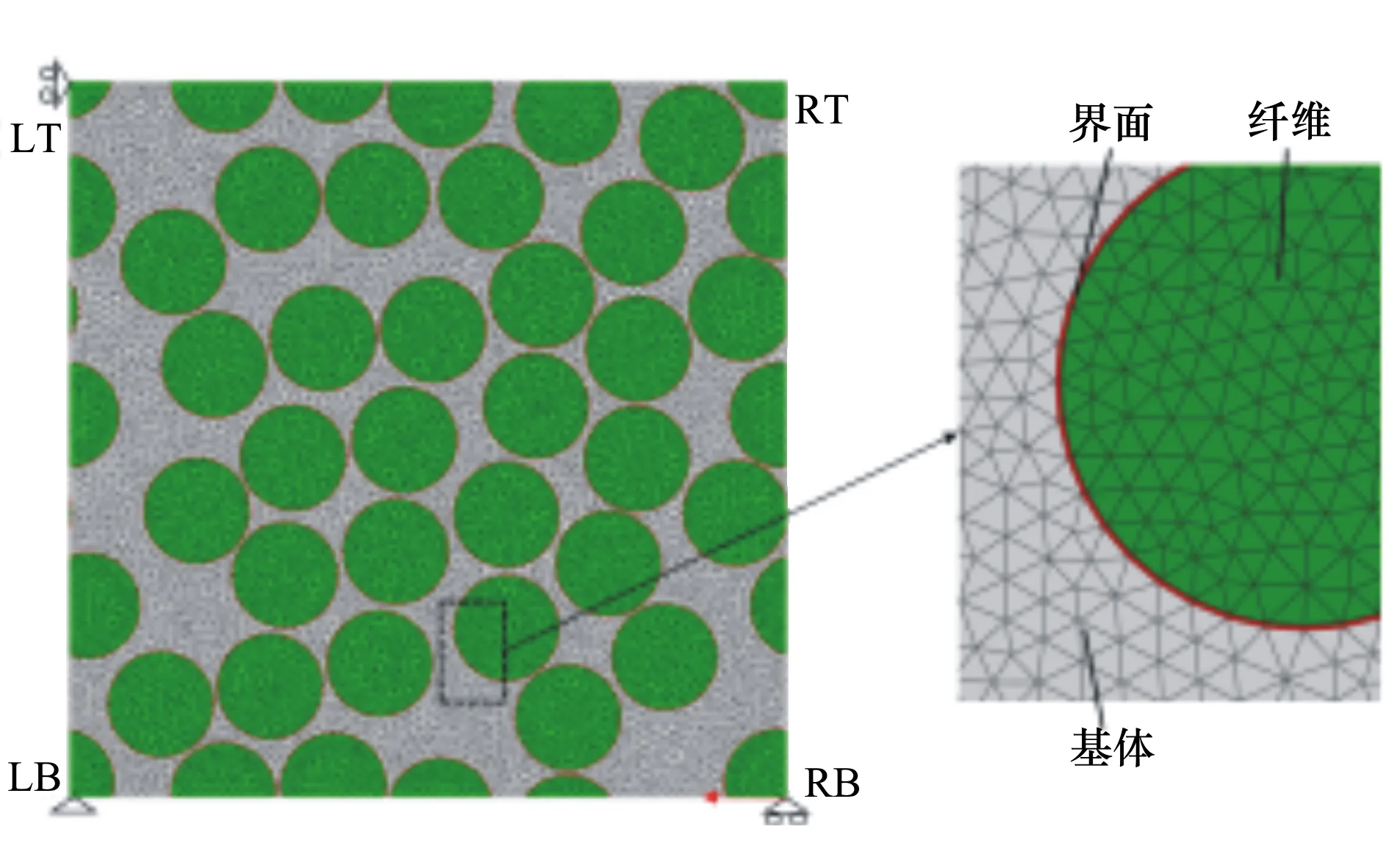
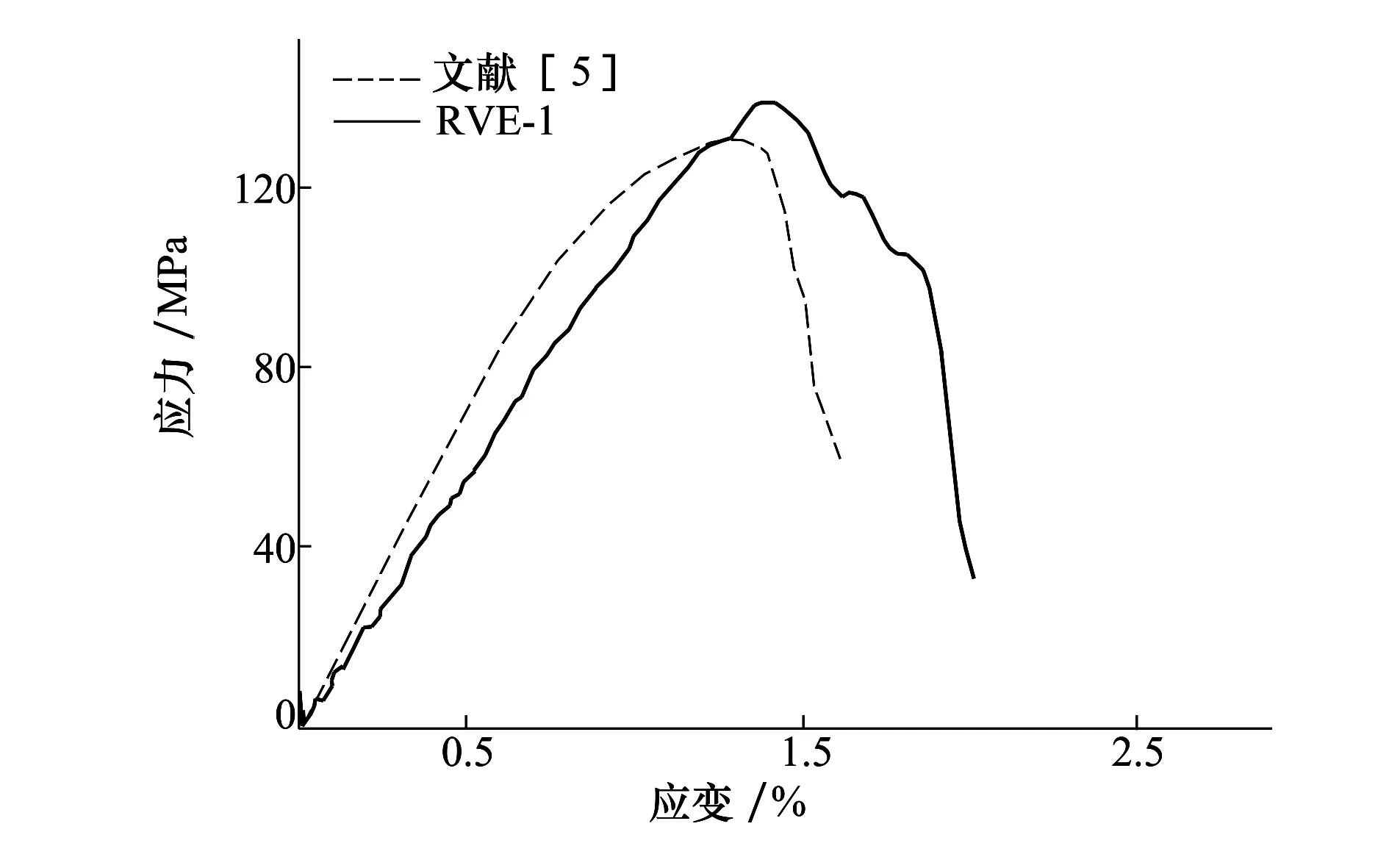
3) 生成第二根纖維(x2,y2)。此點位置由(x2,y2)與當前纖維(x1,y1)之間的距離l和夾角θ決定,l和夾角θ為隨機數,滿足lmin+2r 4) 重復步驟3),直到在當前纖維周圍不能再生成新的纖維。判斷新生成纖維與已生成纖維之間距離是否小于lmin,若小于則刪去此纖維嘗試重新生成。若嘗試次數達到規定,則進行步驟5); 5) 選取第二根纖維為當前纖維,重復步驟3)和步驟4); 6) 對于每一根纖維都重復步驟3)~步驟5),直至纖維體積含量滿足或目標區域已填滿,結束。 本文纖維隨機分布算法采用C++編程,再通過python語言在Abaqus中參數化生成包含纖維、基體和界面的復合材料RVE模型。 為了準確預測復合材料的宏觀力學性能,RVE模型必須包含足夠多的纖維。文獻[6]指出RVE模型包含至少30根纖維時足以表征材料的性能。本文采用上述算法生成5組不同的纖維隨機分布模型,模型包含36根纖維,纖維半徑為5 μm,體積含量為60%,RVE模型的尺寸為68.7 μm×68.7 μm。其中一組纖維隨機分布RVE模型如圖1所示。 圖1 復合材料纖維隨機分布RVE有限元模型 有限元模型采用平面應變單元CPE3劃分基體和纖維網格,以及二維單元COH2D4劃分界面網格,每個模型平均包含單元數約19 000。為了克服非線性數值求解中的收斂性問題,基于Abaqus/explicit進行RVE模型的準靜態分析,設定模型質量放大系數為1 000,以保證準靜態求解的同時減小計算時間。 RVE模型施加周期性邊界條件,在相對平行的2條邊以及角點上滿足 (1) 式中,u表示邊界上節點的位移向量,下標L,R,T,B代表4條邊,LB,LT,RB,RT代表4個角點,如圖1所示。在Abaqus中通過“equation constraint”來實現公式(1)。同時分別約束角點RB和LT的水平自由度和豎直自由度,固定角點LB,以限制RVE模型的剛體運動。角點RB處施加水平位移載荷,如圖1所示。 樹脂基體在橫向壓縮載荷作用下表現出明顯的彈塑性力學行為,并且其屈服行為對靜水壓力敏感。結合擴展的線性D-P屈服準則和塑性準則模擬基體材料在靜水壓力下的塑性以及損傷退化力學行為,D-P屈服準則控制方程為 F=t-ptanβ-d=0 (2) 式中,p為靜水壓力,q為Mises等效應力,r為偏應力第三不變量,β和d分別是D-P準則的內摩擦角和黏聚力。k是三軸拉伸強度與三軸壓縮強度之比,引入了基體材料在拉伸和壓縮情況下不同的屈服行為。k為0.78,β為19.11°,d為83.1 MPa。 M-C屈服準則同樣對基體的彈塑性行為進行了描述,非相關聯流動法則中M-C準則參數可以通過與D-P準則的相互轉換關系(3)式獲得 (3) 式中,φ,c分別為M-C準則的內摩擦角和黏聚力。 采用塑性準則定義材料初始損傷的等效塑性應變εpl,它表示為應力三軸度η的函數。η刻畫了不同的三維應力狀態,取0,1/3,-1/3分別表示純剪切、單軸拉/壓等應力狀態,對應的εpl分別為0.5,0.05和0.5[10]。初始損傷發生后,基體表現出脆性斷裂,取斷裂能Gm=0.5 kJ/m2。 纖維/基體的界面采用經典的雙線性內聚力單元表征其損傷起始與退化的力學行為 (4) (5) (4)式為初始損傷控制方程,(5)式為損傷擴展控制方程。T和G分別表示為界面應力與能量釋放率,下標n,t,s分別表示正向和2個切向方向。選取內聚力單元的初始剛度K=108GPa[5]。界面正向強度Tn0=120 MPa,與基體壓縮強度相同,切向強度Ts0=180 MPa,正向斷裂能Gnc=3 kJ/m2,切向斷裂能Gsc=6 kJ/m2。 為了驗證所建立的RVE有限元模型在預測復合材料橫向壓縮強度的準確性,選取試驗中復合材料E-glass/MY750作為研究對象[16]。文獻[5]對該材料進行了有限元數值仿真,與本文仿真結果進行對比驗證。纖維E-glass彈性模量Ef=74.0 GPa,泊松比vf=0.2,在橫向壓縮載荷作用下認為不發生破壞[5,8]。基體彈性模量Em=3.35 GPa,泊松比vm=0.35,拉伸強度σmt和壓縮強度σmc分別為80 MPa和120 MPa。 圖2所示為RVE有限元模型預測的橫向壓縮應力-應變曲線與文獻[5]仿真結果的對比。可以看出,RVE模型預測的復合材料橫向壓縮強度為138.8 MPa,與文獻[16]中試驗值145 MPa的誤差在4.3%以內,比文獻[5]仿真結果更接近試驗值,說明本文所建立的RVE模型可以很好地預測單向復合材料橫向壓縮強度。 圖2 復合材料橫向壓縮應力-應變曲線 本文RVE模型與文獻[5]預測的失效應變都略高于試驗的失效應變1.2%,這主要是由于數值仿真假設基體的硬化模量為零,而實際上在橫向壓縮載荷作用下,單向復合材料中基體會產生塑性硬化,延性減弱,進而使得失效應變下降。 為了研究纖維隨機分布對單向復合材料橫向壓縮力學性能的影響,建立5組不同纖維分布的RVE模型進行分析,計算獲得在橫向壓縮載荷作用下復合材料的應力-應變曲線如圖3所示。 圖3 不同纖維分布形式預測的復合材料橫向壓縮應力-應變曲線 由應力-應變曲線可以看出,5組曲線在彈性段幾乎重合,隨著初始損傷的發生,曲線開始分離,且隨著應變的增大差別越來越明顯,最終導致壓縮強度出現差異。這主要是因為各組RVE模型中纖維分布位置、尤其是纖維間最近距離分布不同,使得初始損傷產生區域以及最終破壞路徑出現不同,從而引起復合材料應力-應變曲線以及橫向壓縮強度的差別。 表1 不同纖維分布形式預測的復合材料橫向壓縮強度與試驗值誤差 表1列出了5組纖維分布形式預測的復合材料橫向壓縮強度與試驗值的誤差。可以看出5組纖維分布形式的預測結果與試驗值較為吻合,最大誤差為6.2%,說明本文RVE模型尺寸以及界面強度的取值可以很好地預測單向復合材料的宏觀強度性能。但不同纖維分布之間預測的橫向壓縮強度存在偏差,模型RVE-2與RVE-4之間的偏差達到8.5%。由此可見為了更準確地預測單向復合材料力學性能以及損傷破壞形貌,需要建立符合真實微觀纖維分布特征的RVE模型。 為了對比現有研究中界面強度的3種選取方案對復合材料橫向壓縮力學性能的影響,選取界面強度Tn0分別為: a) M-C準則的黏聚力 根據關系(3)式可以獲得為49 MPa; b) 基體壓縮強度 基體壓縮強度為120 MPa; c) 根據試驗數據反演界面強度 通過選取不同界面強度,仿真獲得相應的復合材料橫向壓縮強度。比較發現當界面強度為140 MPa時,復合材料橫向壓縮強度與試驗值最為吻合,因此選擇140 MPa作為反演法得到的界面強度。 3種界面強度選取方案預測的復合材料橫向壓縮強度以及與試驗值的誤差如表2所示。 表2 3種界面選取方案預測的復合材料橫向壓縮強度與試驗誤差 可以看出,界面強度為M-C準則黏聚力時對復合材料橫向壓縮強度的估值明顯偏低。隨著界面強度提高,復合材料橫向壓縮強度升高,并且逐漸逼近試驗值。這說明此時在橫向壓縮載荷作用下,界面損傷對復合材料橫向壓縮強度預測精度產生了影響。 方案c中界面強度140 MPa時預測的橫向壓縮強度顯然與試驗值的誤差最小。此時復合材料壓縮強度基本不再隨界面強度增大而變化,這說明實際上基體塑性損傷,而不是界面損傷在復合材料橫向壓縮破壞過程中起主導作用,這一結論也與文獻[6]得到的結果相符。 圖4進一步給出了界面強度為140 MPa時,復合材料在橫向壓縮載荷作用下的損傷斷裂形貌。可以看出在橫向壓縮載荷作用下,復合材料最終形成與加載垂直方向成48°的剪切斷裂帶。這與M-C彈塑性理論計算得到的基體斷裂角50.8°相吻合[5],說明基體剪切塑性斷裂是引起復合材料橫向壓縮破壞的主要因素,而界面損傷只是在基體出現損傷的局部區域內由于應力集中引起的。 由上述分析可知,復合材料在實際壓縮破壞過程中,界面損傷不是導致材料破壞主要因素,此時繼續增大界面強度仿真得到的復合材料橫向壓縮強度基本不再升高。因此本文采用一種忽略界面單元的有限元模型,用此簡化的無界面單元模型仿真得到的復合材料橫向壓縮應力-應變曲線以及損傷破壞形貌如圖5所示。可以看出,無界面單元模型預測的復合材料橫向壓縮強度為142.9 MPa,與試驗值最為吻合,誤差僅為1.4%。同時在橫向壓縮載荷作用下復合材料最終斷裂形貌與界面強度為140 MPa時的情況相近。這說明了通過準確描述基體的塑性損傷退化行為,無界面單元可以更好地預測單向復合材料的橫向壓縮力學性能,避免了數值仿真中界面參數選取的不確定性問題。 圖5 無界面單元模型預測的復合材料橫向壓縮應力-應變曲線及破壞形貌 1) 本文建立的纖維隨機分布代表性體積單元微觀力學模型可以準確預測單向復合材料的力學性能與損傷形貌。 2) 纖維隨機分布會引起復合材料損傷初始位置與斷裂路徑改變,是引起復合材料橫向壓縮強度差異性的一個因素。 3) 基體塑性損傷而不是界面損傷在復合材料橫向壓縮破壞過程中起主導作用。通過準確描述基體的塑性損傷退化行為,無界面單元可以很好地預測單向復合材料的橫向壓縮力學性能,避免了數值仿真中界面參數選取的不確定性問題。1.2 FEM有限元模型
1.3 基體與界面本構關系
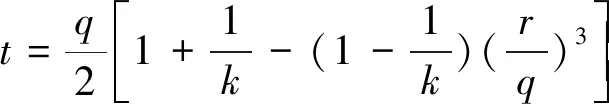
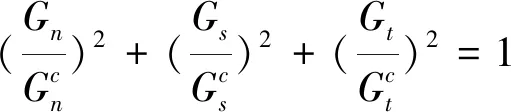
2 橫向壓縮性能計算及結果分析
2.1 RVE模型驗證
2.2 纖維分布對復合材料橫向壓縮力學性能的影響
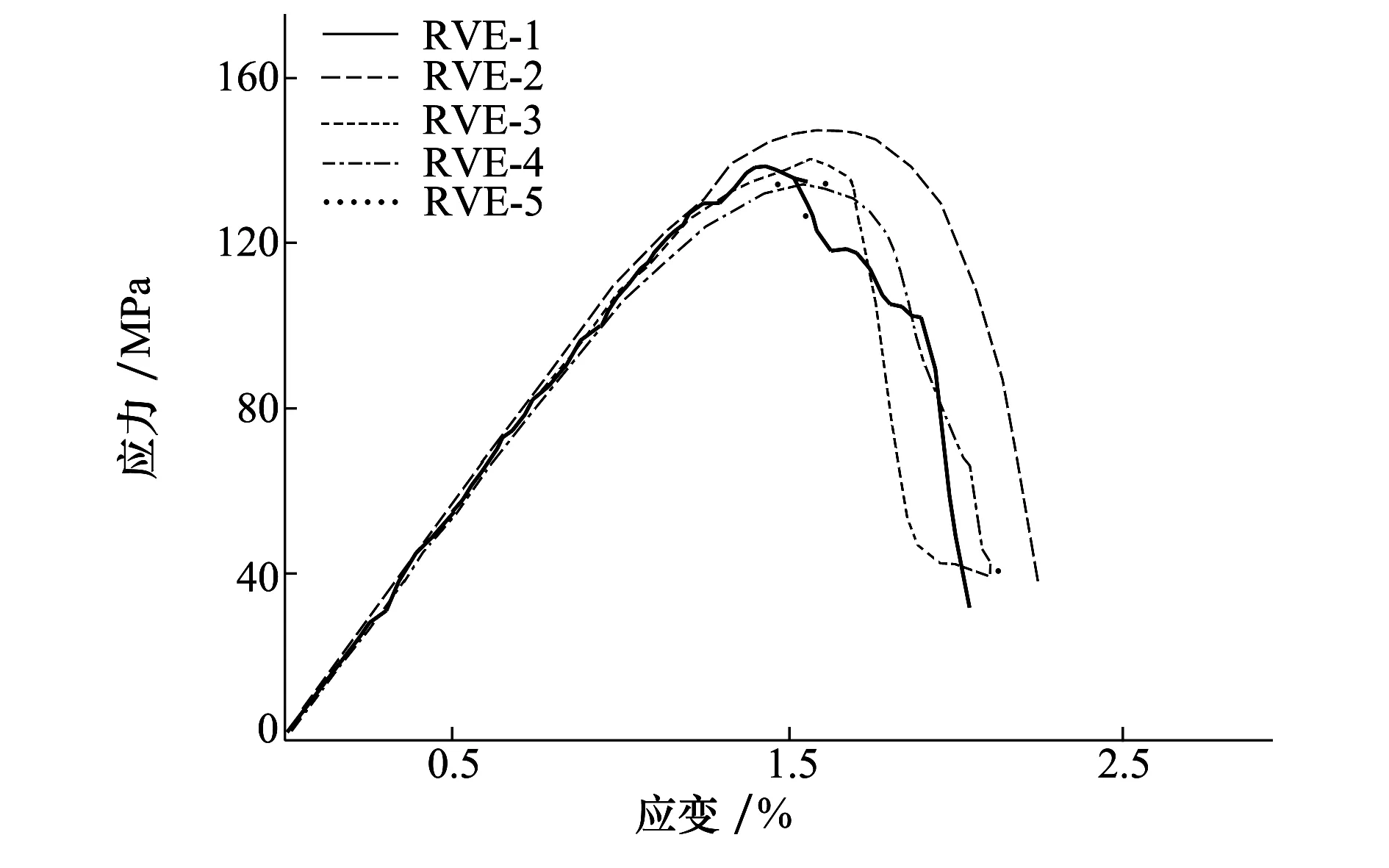
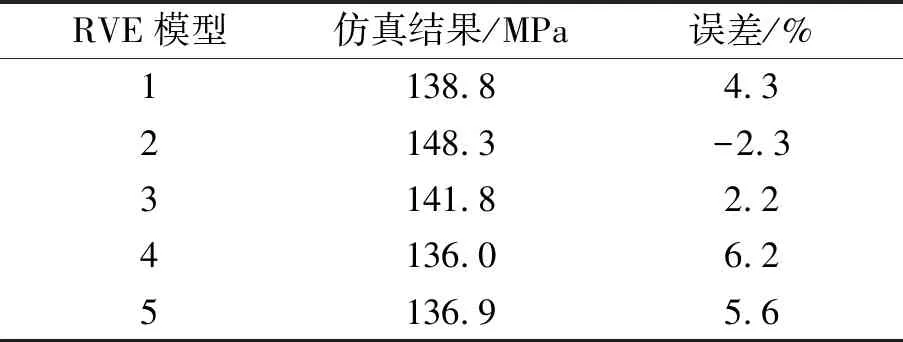
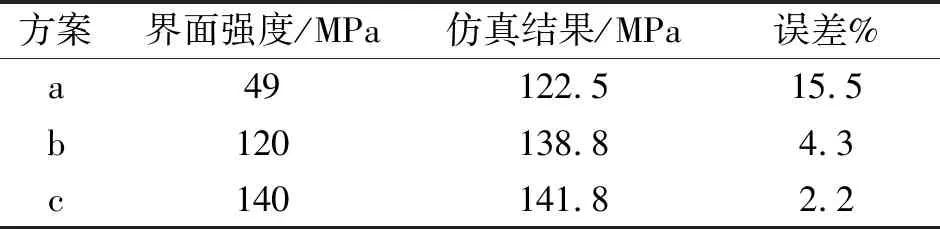
2.3 界面強度對復合材料橫向壓縮力學性能的影響
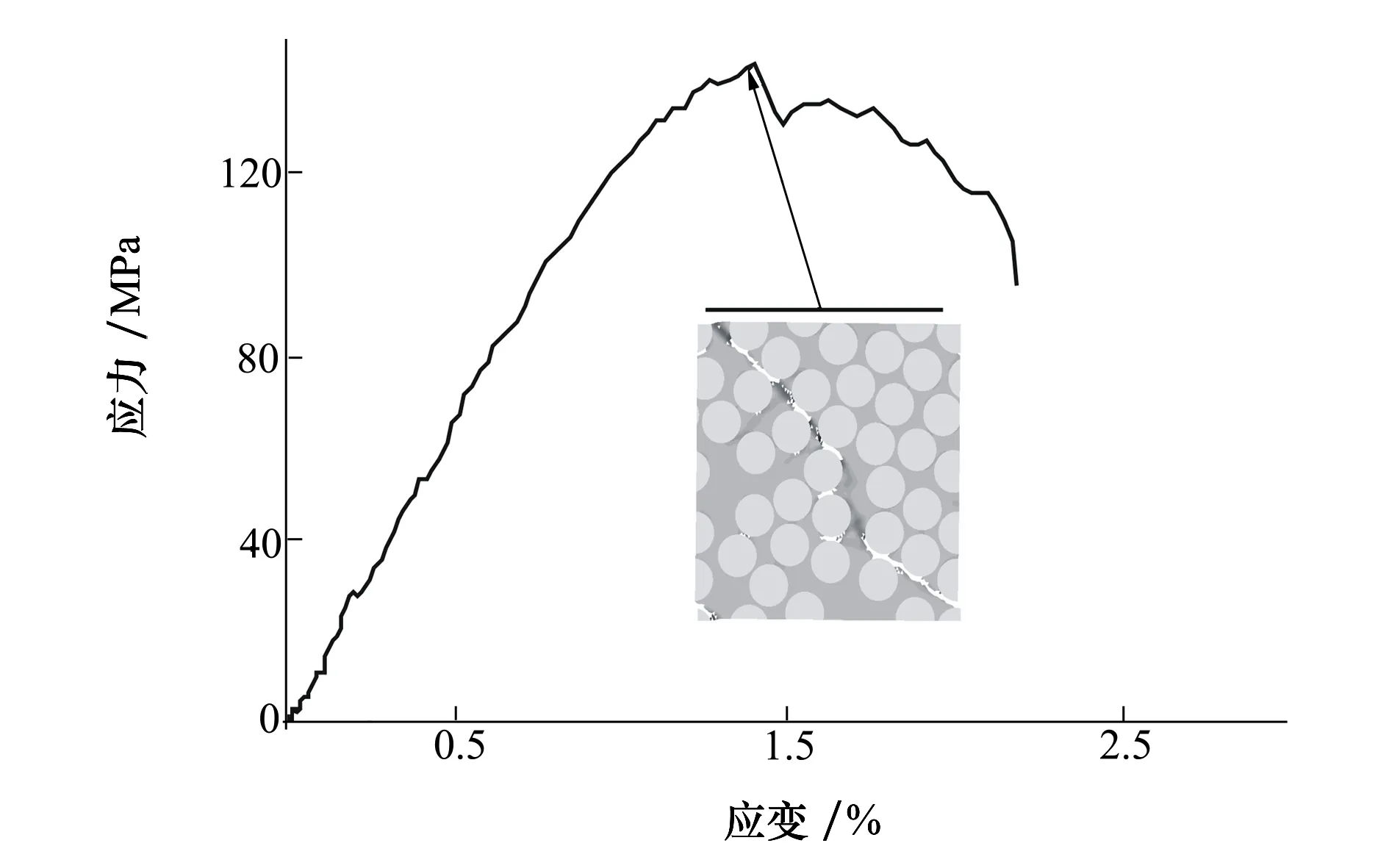
3 結 論

