基于突防效能的導彈-目標分配求解算法

齊長興，畢義明，李 勇

(火箭軍工程大學， 西安 710025)

導彈作戰時面臨著彈道導彈防御系統的攔截，充分運用各種突防技術可以提高導彈突防效能，同時，合理分配導彈，對敵方導彈防御系統進行壓制，也是提高導彈作戰效能的重要手段。以提高導彈突防效能為目的，合理進行導彈-目標分配是一種典型的武器-目標分配(Weapon，Target，Assignment，WTA)問題，就是在作戰資源一定的情況下，通過對進攻導彈(主突導彈、輔攻導彈)合理配置，對敵方導彈防御系統進行壓制，通過對輔攻導彈的合理配置和戰術運用，提高導彈突防效能。

WTA問題是一個典型的NP完全問題[1]，隨著規模的增加，問題的求解時間呈指數級增長。傳統的算法在解決這類問題時較為困難，當前主要采用啟發式算法求解。文獻[2]提出了離散粒子群優化求解WTA問題的方法；文獻[3]提出了求解WTA問題的局部協同控制方法；文獻[4]將MOPSO (Multi-object Particle Swarm Optimization， MOPSO) 和TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)結合，進行多目標武器目標分配問題求解；文獻[5]提出了一種自適應并行群選擇算法解決武器目標分配問題，取得了較好的應用效果；文獻[6]建立了基于改進型多目標粒子群優化算法，應用于較大規模的WTA問題實時求解等。但是這些算法不同程度上存在早熟收斂、進化速度慢及計算復雜等問題，在實際問題應用中還需要進行調整優化。

基于突防效能的導彈-目標分配問題是在給定作戰條件下，以導彈防御系統為作戰目標，合理分配火力使得主突導彈突防效能最高。本文構建了基于突防效能的導彈-目標分配模型，并以粒子群算法為主體，采用混沌優化策略和禁忌搜索策略對粒子群算法進行優化，構建改進的混合粒子群算法對模型進行求解，案例分析驗證了方法的可行性。

1 導彈-目標分配問題描述與建模

設m為導彈武器的種類，Mi(i=1,2,3,…,m)為第i種導彈武器的數量；n為導彈防御體系中作戰主體(例如，預警衛星、預警機、雷達、反導導彈、電子戰裝備、電磁武器等)數量。l為防御系統體系中作戰主體類型數，nj(j=1,2,3,…,l)為第j種作戰主體的數量。第i類導彈對防御體系中第j個作戰主體毀傷概率為eij。引入WTA矩陣，分配矩陣X和毀傷概率矩陣E分別為：

(1)

(2)

xij=1表示分配了第i個導彈武器打擊敵j個目標，否則xij=0。eij表示第i個導彈武器打擊敵j個目標使得毀傷概率。

針對導彈防御系統中不同的作戰主體對導彈防御系統整體功能發揮的作用重要度不同，對不同的作戰主體進行打擊后，提高導彈突防效能的程度不同，本文引入突防貢獻度的概念，對導彈突防作戰效果進行評價。突防貢獻度即：對導彈防御系統中某個作戰主體(節點)進行打擊后，對導彈突防效能提高的貢獻，用[0,1]區間的實數表示突防貢獻度的大小。考慮突防貢獻度后，導彈-目標火力分配模型可以表示為：

(3)

式中，F為導彈突防的效益函數；Cj為第j個作戰主體被打擊后的突防貢獻度，采用專門的評價方法進行確定。

2 改進的混合粒子群優化算法

粒子群優化(Particle Swarm Optimization，PSO)算法具有良好的全局和局部搜索能力[7]，在求解問題優化時得到了很好的應用。但是粒子群優化算法后期容易陷入早熟收斂，局部尋優能力不高。本文提出了一種基于混沌優化與禁忌搜索策略的混合粒子群優化算法[8]。采用混沌優化方法生成初始種群，以保持種群多樣性；采用禁忌搜索策略，以提高搜索效率，避免了基本粒子群優化算法中存在的易于陷入局部最優的問題。

2.1 Tent混沌映射模型

Logistic映射和Tent映射在混沌系統中具有較為廣泛的應用，Tent映射比Logistic映射的遍歷性和迭代速度更快[9]。因此，采用Tent映射產生混沌序列，其表達式為：

z(t+1)=T(z(t))=

(4)

式中，z(t)∈[0,1]。

Tent映射在迭代過程中存在小周期(0.2,0.4,0.8,0.6)，以及在不穩定周期點0.25,0.5,0.75將迭代到不動點0。為避免該現象的出現，對tent映射進行改進，改進后的tent映射為：

當z(t)=0，0.25,0.5,0.75，或z(t)=z(t-k)，k=0,1,2,3,4時，z(t+1)=z(t)+0.01·rand(0,1)

Tent映射混沌序列生成的步驟如下：

步驟1初始化，隨進生成n個[0,1]區間的隨機數。

步驟2進行混沌變換。

根據混沌模型，進行混沌變換，生成n個混沌變量。

步驟3將混沌變量映射到變量區間。

將混沌序列映射到變量空間[xjmin,xjmax]，得到初始種群中第i個體的第j個分量xij，xij=xjmin+(xjmax-xjmin)·zij。

2.2 粒子群優化算法

1) 算法描述

基本PSO算法的數學描述為：N維搜索空間中，種群位置為X={x1,x2,…,xn}T，第i個粒子位置為xi=(xi1,xi2,…,xin)，速度為vi=(vi1,vi2,…,vin)。在迭代過程中，通過跟蹤個體的最優位置和全局最優位置來更新個體的速度和位置，設pi為第i個粒子所經歷的個體最優位置，pi=(pi1,pi2,…,piN)，pg為全局最優位置，pg=(pg1,pg2,…,pgn)。

PSO算法的進化方程為：第t代粒子的第n維速度和位置由以下公式計算：

vin(t+1)=ωvin(t)+c1r1(pin(t)-xin(t))+

c2r2(pgn(t)-xin(t))

(5)

xin(t+1)=xin(t)+vin(t+1)

1≤i≤M,1≤n≤N

(6)

式中，vin(t)表示第i個粒子的第n維在第t次迭代中的位置和速度；ω為慣性權重，c1、c2為學習因子，r1、r2為[0,1]區間內的隨機數；-vmax≤vin(t)≤vmax，vmax為預先設定的最大迭代步長。

對于目標分配問題，需要對粒子的位置和速度取整，使搜索在整數域中進行，對速度分量進行修訂，如公式所示。

vin(t+1)=int[ωvin(t)+c1r1(pin(t)-xin(t))+

c2r2(pgn(t)-xin(t))]

(7)

xin(t+1)=xin(t)+vin(t+1)

1≤i≤M,1≤n≤N

(8)

2) 編碼和解碼

為保持種群多樣性和個體均勻分布，采用Tent混沌映射初始化種群。首先利用Tent混沌映射生成混沌序列，然后將混沌序列映射到解空間，最后對所有解排序，將適應度較優的作為初始化種群的解。

根據要解決的問題的需要，對PSO算法中的粒子進行編碼，并滿足約束條件，采用實數編碼方式進行編碼。PSO粒子編碼方案如圖1所示。

圖1 PSO算法編碼方案

圖1表示n類導彈打擊m個目標的編碼，Xij表示第i類導彈打擊第j個目標的數量。每個目標對應一個基因段，每個基因段長度為n，則編碼的長度為m×n。

3) 參數設計

取目標函數為適應度函數。

(9)

1) 慣性權重，

慣性權重取值大小影響算法的搜索能力，為了平衡全局搜索和局部搜索能力，設計自適應慣性權重。在算法早期采用較大的慣性權重，以保證較強的全局搜索能力；在算法后期采用較小的慣性權重，可以提高局部搜索精度。

根據全局最優值的變化情況自適應調整慣性權重，調整策略如下：

ω(t)=(1+e-k)-1

(10)

式中，ω(t)為第t次迭代時慣性權重，k為進化速度因子。

(11)

式中，fg(t)為第t代全局最優值的適應度。

2) 學習因子優化

對學習因子進行混沌處理，以提高算法的收斂速度。

Ci(t+1)=Cmin+(Cmax-Cmin)·zi(t+1)

(12)

式中，Ci(t)∈[1.4,2]。

4) 早熟處理

粒子群算法迭代后期，收斂速度降低，易于陷入局部最優，出現早熟現象，當出現早熟現象時，對粒子進行混沌優化，使其跳出局部最優，提高全局搜索能力。

設定一個計數器P，用于統計當前全局最優解連續出現的次數。給定一個閾值c，如果p=c則認為出現局部最優，陷入早熟。

當粒子群出現早熟現象時，采用Tent混沌映射對當前生成的粒子進行混沌優化，使其跳出局部最優值。

步驟1采用Tent混沌映射對當前全局最優值進行混沌變換；

步驟2計算混沌變換后適應度值，與當前全局最優解比較，取較優解作為當前全局最優解；

步驟3判斷是否終止條件，如果滿足則輸出最優解，否則轉到步驟1。

2.3 禁忌搜索策略

TS(Tabu Search) 算法是一種全局逐步尋優的亞啟發式搜索算法，并得到了較好的發展[10]。TS算法通過設置禁忌表，避免對局部最優解的重復搜索，同時通過設置“特赦準則”，保持搜索過程的多樣性。

禁忌搜索算法的基本過程如下：

步驟1設置禁忌表(tabu list)H=?，并選定一個初始解X′；設置禁忌長度Tmax、終止條件、候選集Can_N(X′)等。

TS算法對初值依賴性較強，可以用PSO算法產生的性能優良的解作為TS算法的初值，有利于進行禁忌搜索，提高搜索速度；同時禁忌搜索到的解為PSO算法提供較好的粒子，提高全局搜索能力。

2.4 改進的混合粒子群優化(HPSO)算法流程

改進的混合PSO算法的基本思想是，以PSO算法為主體，通過混沌序列對粒子速度和位置進行初始化生成初始種群；設定自適應慣性權重，平衡全局搜索能力和局部搜索能力；采用混沌序列生成學習因子；通過對粒子的速度和位置優化獲得尋優目的。在粒子進化過程中引入禁忌搜索策略，避免對粒子的重復訪問，提高了搜索效率；通過早熟判斷機制進行早熟判斷，通過混沌優化使其跳出局部最優，提高算法的全局搜索能力。算法流程如圖2所示。

算法基本步驟如下：

步驟1初始參數設置。規模、最大迭代次數、控制變量、禁忌長度、特赦條件。

步驟2種群初始化，采用混沌優化方法生成初始種群。

步驟3進行種群編碼，設置禁忌表為空。

步驟4計算適應度值。

步驟5粒子尋優，根據粒子群的狀態，確定粒子群的個體最優位置和全局最優位置，更新粒子的個體最優值和全局最優值。

步驟6判斷是否滿足終止條件，如果滿足則進行解碼、輸出結果，否則繼續進行迭代。

步驟7確定候選解，確定當前最優解為候選解，并將其加入禁忌表中，更新禁忌表，用當前的候選解替換最早進入禁忌表的解。

步驟8判斷候選解是否滿足特赦準則，如果滿足，則將解禁解作為當前最優解，更新禁忌表和當前狀態，轉入步驟4；否則，執行下步操作。

步驟9判斷候選解的禁忌屬性，選擇最佳解為當前解，更新禁忌表，轉入步驟4。

步驟10判斷是否滿足終止條件，如果滿足停止迭代，輸出最優解；否則轉到步驟4。

圖2 算法流程

3 算例分析

3.1 算例設置

A國在XX島部署了彈道導彈防御系統，包括早期預警衛星1部(D1)，預警雷達1部(D2)，指控中心1部(D3)，攔截彈系統1套(D4)，電子對抗裝置一部(D5)，共5個目標。

C國導彈作戰集團主作戰導彈型號為X型彈道導彈，輔助攻擊導彈為A型和B型常規彈道導彈，A型導彈數為15，B型導彈數為10，作戰策略為采用輔攻導彈進行第1波次攻擊，對導彈防御系統進行打擊，降低其對X型導彈的攔截能力。

通過專家打分法對導彈防御系統中作戰主體的突防貢獻度打分，經過歸一化處理得到突防貢獻度如表1所示。

表1 突防貢獻度

導彈對目標的毀傷概率是指導彈突破敵方防御后成功毀傷目標概率，如表2所示。

表2 毀傷目標概率

仿真環境為：Windows7 64位操作系統，3.50 GHz處理器，8G內存，Matlab R2014a仿真平臺。分別用粒子群優化算法(PSO)、混沌優化粒子群算法(CPSO)、禁忌搜索粒子群算法(TSPSO)及改進的混合粒子群優化算法(HPSO)進行仿真運算，均采用實數編碼方式進行編碼。主要參數設置為：各算法的種群規模為30，最大迭代次數為100；PSO算法中慣性權重為0.7，學習因子為1.49；TSPSO算法中禁忌表長度為5，特赦準則采用“best so far”準則解禁最優解，慣性權重為0.7，學習因子為1.49；HPSO算法初始慣性權重為0.7，初始學習因子為1.49，早熟判斷閾值為3。

3.2 仿真結果分析

分別采用粒子群優化算法(PSO)、混沌優化粒子群算法(CPSO)、禁忌搜索粒子群算法(TSPSO)及改進的混合粒子群優化算法(HPSO)進行仿真運行100次，

分別采用4種算法進行仿真運行100次，得到適應度平均值，適應度變化曲線如圖3所示。

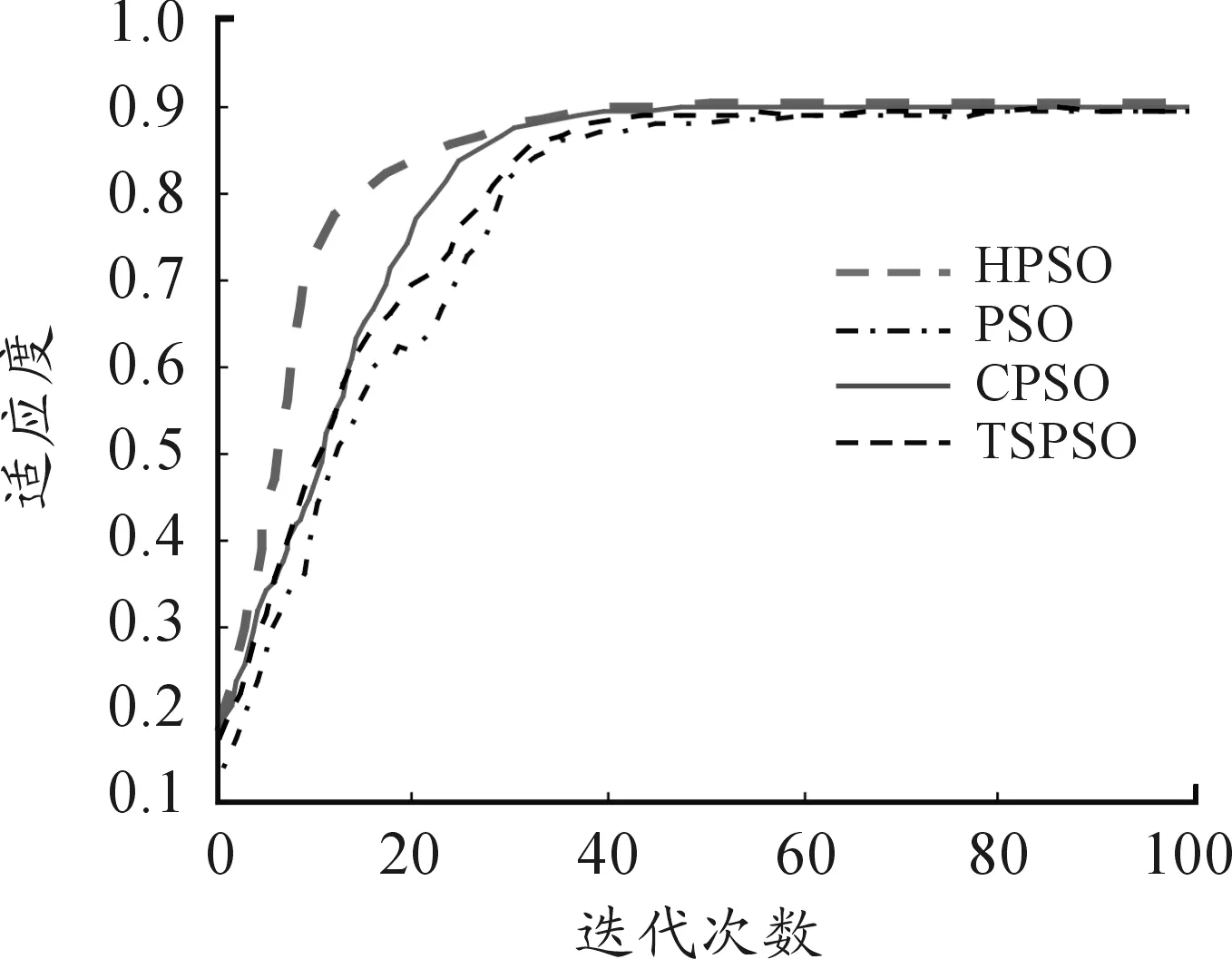
圖3 平均適應度值變化曲線

圖3描述了分別采用四種算法進行問題求解是時適應度變化情況，通過仿真分析可知，與PSO算法、CPSO算法和TSPSO算法相比，HPSO算法收斂速度最快，可以較快的獲得全局最優解，而且采用HPSO算法獲得的全局最優解優于PSO算法、CPSO算法和TSPSO算法。

分別采用4種算法獲得的最優導彈火力目標分配結果如表3～表6所示。

表3 混合粒子群算法得到的導彈-目標分配結果

表4 混沌優化粒子群算法得到的導彈-目標分配結果

表5 禁忌搜索粒子群算法得到的導彈-目標分配結果

表6 粒子群算法得到的導彈-目標分配結果

采用HPSO算法獲得的導彈-目標分配方案對應的最優適應度值為0.903，即經過先期打擊，后續突防導彈的突防效能可以達到0.903；采用CPSO算法獲得的導彈-目標分配方案對應的最優適應度值為0.902，即經過先期打擊，后續突防導彈的突防效能可以達到0.902；采用TSPSO獲得的導彈-目標分配方案對應的最優適應度值為0.896，即經過先期打擊，后續突防導彈的突防效能可以達到0.895。可知，采用HPSO算法獲得的導彈目標分配方案適應度值最大，效果最好。

4 結論

1) 通過案例分析和仿真試驗表明，改進的混合粒子群優化算法具有較好的收斂性，適用于求解導彈目標分配問題。

2) 本文未考慮火力打擊動態過程中目標毀傷后對目標分配的影響，突防貢獻度的賦值具有一定的主觀性，下一步將對這方面的問題加強研究。