輸電線路后注漿微型鋼管樁基礎注漿厚度研究

李春燕,徐運生,李占嶺,王 勝

(1.華北電力大學 機械工程系,河北 保定 071003; 2.中國電建集團 河北省電力勘測設計研究院有限公司,石家莊 050031)

目前,對微型鋼管樁研究主要集中于房屋加固和邊坡處理等工程.馬周全[1]通過有限元分析對微型鋼管樁的極限抗滑力進行研究.李湛等[2]通過鋼管樁抗壓靜載檢驗，研究了微型鋼管樁對既有建筑的加固作用.向波等[3]通過對微型鋼管排樁結構現場堆載極限破壞試驗,獲取了支擋結構的樁身變形、樁身應變、土壓力等數據,分析總結了鋼管排樁承受水平載荷的受力變形規律.宗鐘凌[4]提出了一種微型靜壓鋼管樁注漿成樁工藝,并對成樁機理及特點進行了分析.但均未對后注漿微型鋼管樁注漿厚度在輸電線路中進行研究.本文通過大型通用有限元軟件Abauqs對后注漿微型管樁進行有限元分析,后注漿微型鋼管樁基礎作用力參照國家電網典型設計2B7-ZM1-27鐵塔的基礎作用力,通過改變微型鋼管樁的數量和注漿厚度,得出最優微型鋼管樁的布樁數量和最優注漿厚度,從而達到經濟、合理、安全.

1 模型尺寸

本文所用模型包括注漿厚度為10,15和20 mm、壁厚為2，3，4 mm的4根后注漿微型鋼管樁,總模型數為9個.

后注漿微型鋼管樁的模型大致分為上部主柱,主柱露頭為200 m,主柱與承臺相連,承臺下部分別與微型鋼管樁進行連接,微型鋼管樁通過內部后注漿充滿鋼管與外部注漿包裹在微型鋼管樁外部,外注漿包裹厚度分別為10,15和20 mm.后注漿微型鋼管樁的尺寸：4根后注漿微型鋼管樁承臺長寬均為1 700 mm,高為500 mm；主柱長寬均為800 mm,高為1 200 mm.4根微型鋼管樁橫向和縱向的鋼管間距為400 mm,鋼管長為6 000 mm,直徑159 mm,壁厚分為2，3和4 mm.具體布置型式如圖1所示.

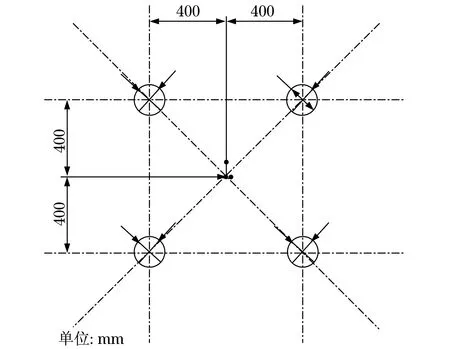
圖1 4根微型鋼管樁布置型式 Fig.1 Layout types of four miniature steel pipe piles

2 后注漿微型鋼管樁模型設置

2.1 分析步的定義

本模型分析步的定義分為初始地應力平衡和靜力分析.由于采用Mohr-Coulomb本構模型,因此,其他設置為非對稱算法.

2.2 接觸的定義

模型接觸定義首先是鋼管內部注漿與鋼管內部表面的綁定約束定義,鋼管外部與外注漿內部的綁定約束定義;其次是后注漿外部、承臺、主柱和土的接觸定義,主控面是后注漿、承臺和主柱,從控面是土.其中的關鍵是地應力的平衡,采取的措施是在地應力分析步采取切向無摩擦和法向硬接觸,在施加荷載后，外注漿與土體切向摩擦為0.4和法向硬接觸,鋼管與注漿間接觸的切向摩擦為0.6和法向硬接觸.

2.3 后注漿微型鋼管樁和土體單元選取、網格劃分、邊界載荷的定義

后注漿微型鋼管樁三維有限元模型采用C3D8單元,4根后注漿微型鋼管樁網格數為8 644個,土體的網格數為53 572個,網格總數為62 216個.4根后注漿微型鋼管樁內注漿、鋼管、外注漿、承臺主柱和土體網格劃分如圖2～圖6所示.內注漿、鋼管、外注漿、承臺主柱和土體網格劃分整體遵循在接觸處劃分較密,土體和樁接觸之外網格劃分較梳.荷載在主柱露頭處施加x方向水平力Tx=29 000 N,y方向水平力Ty=24 000 N,上拔力T=257 000 N.

圖2 內注漿網格Fig.2 Inner grouting grid

圖3 鋼管網格Fig.3 Steel pipe grid

圖4 外注漿網格Fig.4 Outer grouting grid

圖5 承臺網格Fig.5 Platform grid

圖6 土體網格Fig.6 Soil grid

3 力學特性分析

為分析不同注漿厚度的4根微型鋼管樁的受力情況,現將有限元分析得到的位移和彎矩進行分析.

在水平力和上拔力作用下,不同注漿厚度的4根微型鋼管樁橫向位移表現為:10 mm注漿厚度的4根微型鋼管樁最大正向水平位移為0.977 mm,最大負向水平位移為0.085 mm;15 mm注漿厚度的4根微型鋼管樁最大正向水平位移為3.358 mm,最大負向水平位移0.090 mm;20 mm注漿厚度的4根微型鋼管樁最大正向水平位移為0.890 mm,最大負向水平位移為0.365 3 mm.將不同注漿厚度最大正向水平位移和最大負向水平位移整理，如表1所示.

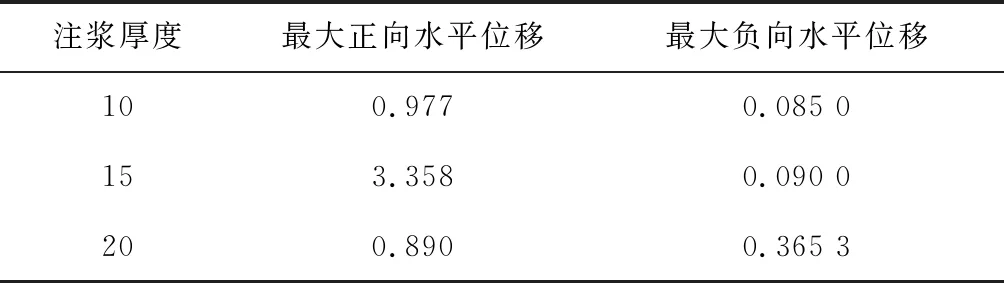
表1 不同注漿厚度最大正向和最大負向水平位移Tab.1 Maximum positive and negative horizontal

通過表1繪制不同注漿厚度的最大正向位移和最大負向位移,如圖7所示.

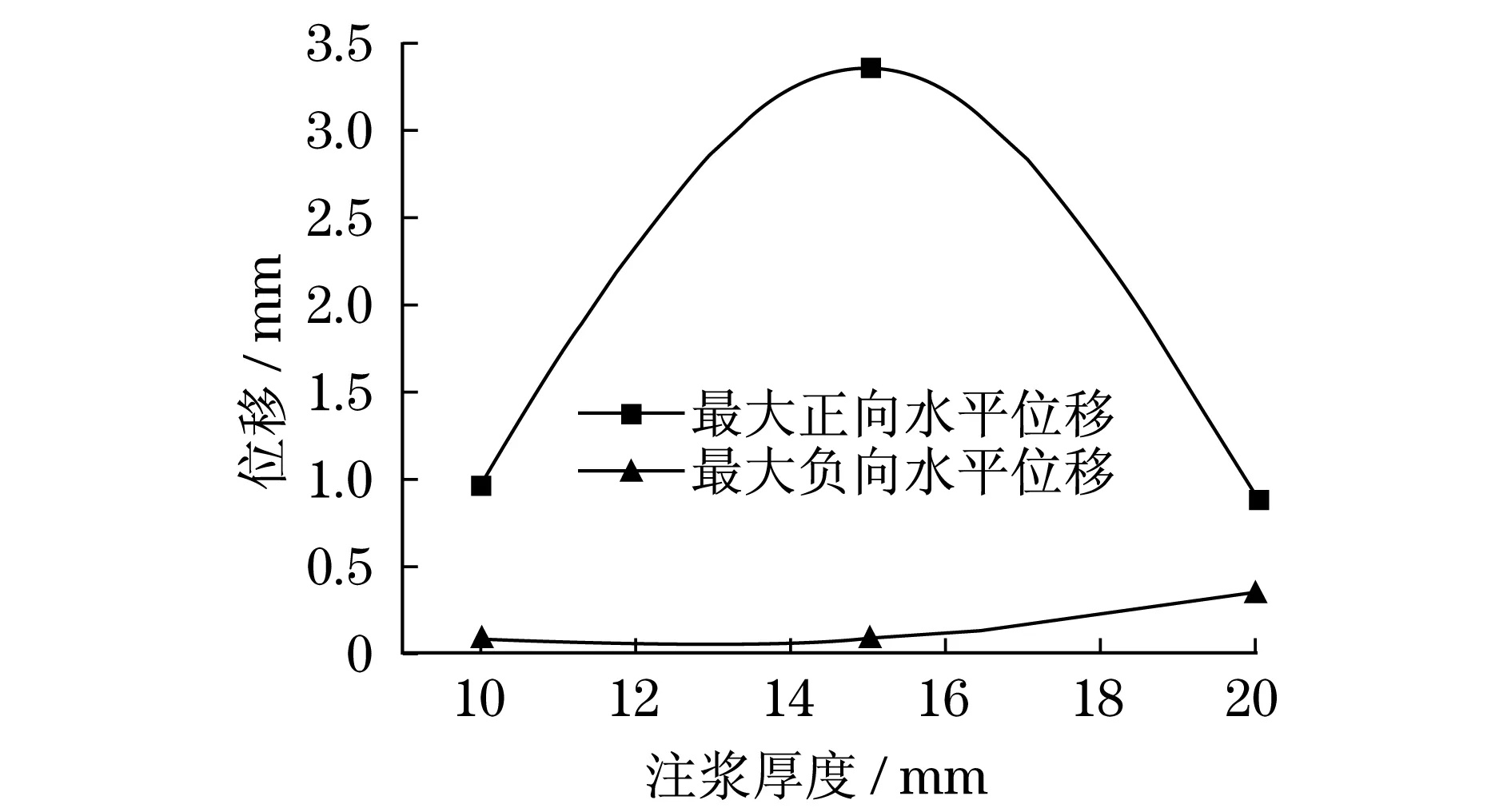
圖7 不同注漿厚度最大正向和負向位移Fig.7 Maximum positive and negative displacements

從圖7中可知:注漿厚度為10和20 mm時,微型鋼管樁最大正向位移較小;注漿厚度為15 mm時,微型鋼管樁最大正向位移最大,此時最大正向位移隨注漿厚度大致呈現二次拋物線的形式;注漿厚度為10和20 mm時，微型鋼管樁位移最小.微型鋼管樁最大負向位移隨注漿厚度的增加而增加.對于最大正向位移,在注漿厚度10～15 mm時,微型鋼管樁最大正向位移注漿增加是由于注漿離鋼管較近,而注漿的變形大于鋼管,導致微型鋼管樁正向橫向位移隨注漿厚度增大而增大;而當注漿厚度在15～20 mm時,由于注漿外層離土較近且離鋼管較遠,而注漿變形小于土的變形,導致微型鋼管樁最大正向位移注漿減小.對于最大負向位移,由于最大負向位移與力的方向相反,微型鋼管對注漿的作用較小,注漿與土的接觸更是考慮的重點,導致最大負向位移值隨注漿厚度的增加而注漿增加.

由以上分析可知,在注漿厚度為10 mm時,微型鋼管樁的最大正向水平位移和最大負向水平位移都較好,因此，從最大水平位移角度,優先選用注漿厚度10 mm的微型鋼管樁.

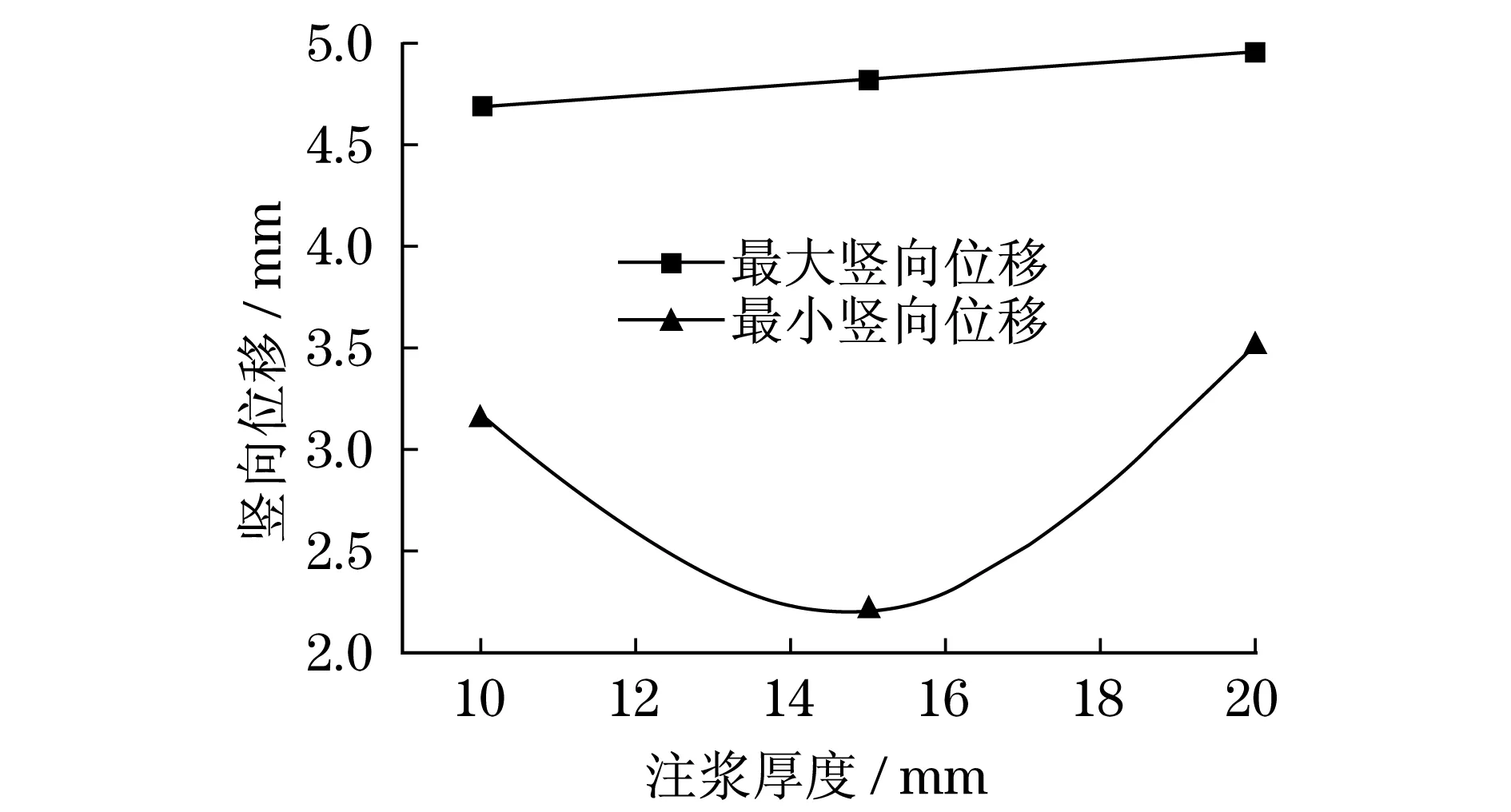
圖8 不同注漿厚度最大和最小豎向位移Fig.8 Maximum and minimum vertical displacement of

由圖8可知，在水平力和上拔力作用下，不同注漿厚度的4根微型鋼管樁豎向位移表現為:10 mm注漿厚度上拔最大位移為4.676 mm,上拔最小位移為3.162 mm;15 mm注漿厚度上拔最大位移為4.808 mm,上拔最小位移為2.206 mm;20 mm注漿厚度上拔最大位移4.948 mm,上拔最小位移3.513 mm.將不同注漿厚度最大豎向位移和最小豎向位移進行整理,如表2所示.

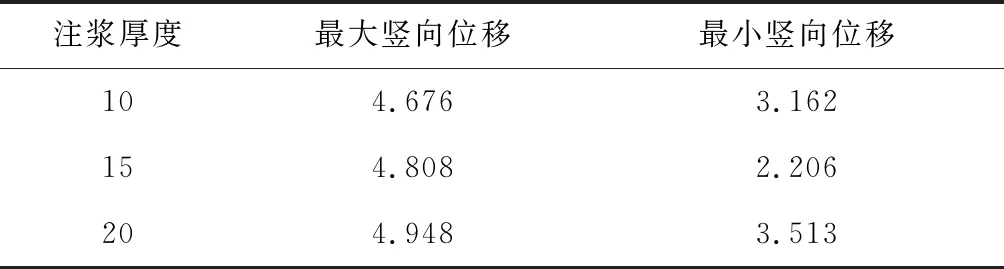
表2 不同注漿厚度最大豎向位移和最小豎向位移Tab.2 Maximum and minimum vertical displacement

由圖8可知,注漿厚度在10～20 mm之間,微型鋼管樁在水平力和上拔力作用下最大豎向位移隨注漿厚度大致呈線性變化,且最大豎向位移隨注漿厚度增大而增大,最小豎向位移隨注漿厚度先減小后增大.通過豎向位移比較得出，10 mm注漿最大豎向位移最小,而15 mm注漿豎向位移總體較為均勻,20 mm注漿厚度最大豎向位移最大且總體位移不均勻.因此,從豎向位移來看,10 mm注漿厚度和15 mm注漿厚度最優.

從水平位移(見圖8)和豎向位移(見圖9)兩者比較可以看出：最大負向水平位移與最大豎向位移呈近似對稱關系,最大正向水平位移與最小豎向位移呈近似對稱關系,從這個變化可以得出最大負向位移與最大豎向位移具有對應關系,最大正向水平位移與最小豎向位移也具有對應關系.由此可以得出,后注漿微型鋼管樁的水平位移與豎向位移具有相關性,從某種程度上可以看出微型鋼管樁的水平位移可以反映出其豎向位移.提取不同注漿厚度的Mx,My彎矩數據,繪制在z方向Mx的彎矩，如圖9所示.

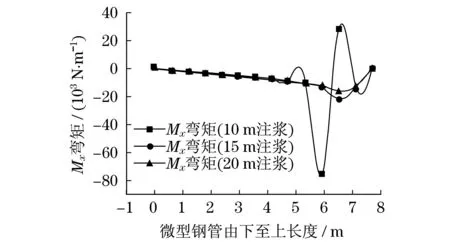
圖9 沿z方向Mx彎矩圖Fig.9 Mx moment diagram along z direction

由圖9可知：不同注漿厚度情況下,微型鋼管樁的彎矩隨深度大致呈線性變化,且隨著深度的增加彎矩值是逐漸減小的,在10 mm注漿厚度微型鋼管樁與承臺連接處彎矩出現正負交替的變化,而在注漿厚度為15和20 mm處彎矩波動較小.彎矩的正負交替變化對基礎的受力是不利的,因此，可以考慮通過補強措施來減小彎矩波動.從本例的分析來看,通過在微型鋼管樁與承臺連接處適當增加注漿厚度來減弱正負交替的彎矩變化是有效果的.

因此可以得出：注漿厚度的變化對x方向的彎矩變化是較小的,僅僅在連接處彎矩出現變化,連接處可通過補強措施來消除.故分析注漿厚度對基礎的影響時,可以不將注漿厚度影響x方向彎矩作為考慮的重點.

提取不同注漿厚度的Mx,My彎矩數據,繪制在z方向My的彎矩，如圖10所示.由圖10可知：My彎矩隨微型鋼管樁長度大致呈線性變化,注漿10 mm的微型鋼管樁在連接處彎矩出現較大波動，且注漿15 mm和注漿20 mm的彎矩在連接處彎矩變化較小.My與上述Mx情況類似,均可通過連接處增加注漿厚度來提高補強措施得以解決.因此,注漿厚度對微型鋼管樁彎矩的影響較小,不必作為主要方面進行考慮.

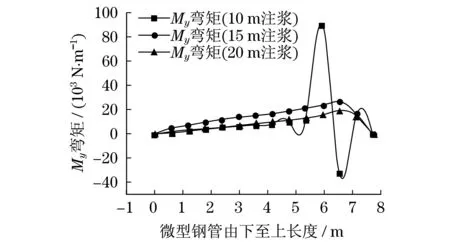
圖10 沿z方向與My彎矩圖Fig.10 My moment diagram along z direction

通過以上分析可以排除彎矩對注漿厚度的影響,現在考慮鋼管直徑和壁厚對注漿厚度的影響.通過大量的有限元數值模擬和理論分析,將鋼管壁厚確定,得出數據繪制不同鋼管直徑最優注漿厚度隨鋼管直徑變化,如圖8所示.

圖11 不同壁厚最優注漿厚度隨鋼管直徑變化Fig.11 The optimum grouting thickness of different

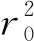
式中:r為注漿厚度;d為鋼管半徑;r0為鋼管壁厚.

通過分析得出的數據再反過來驗證公式的適用性,最優注漿厚度、鋼管直徑和鋼管壁厚較為準確,具有一定的普遍性.

4 結論

本文通過4根微型微型鋼管樁進行力學特性分析,歸納出如下結論:

(1) 微型鋼管樁的最優注漿厚度本質上是注漿、鋼管和土的相對距離而決定的.

(2) 微型鋼管樁在計算注漿厚度時主要考慮在水平力、上拔力作用下的水平位移和豎直位移,這兩方面位移量作為受力考慮的主要方面.

(3) 彎矩Mx,My影響注漿厚度的效果較小,僅在鋼管和承臺連接處彎矩影響較大,可通過增加注漿厚度來減小彎矩影響,故選取最優注漿厚度可不予考慮彎矩Mx,My.

(4) 通過大量的有限元數值模擬,總結出適應于一般性的注漿厚度r、鋼管半徑d和鋼管壁厚r0之間的數值關系,為后期設計人員優選微型鋼管樁的注漿厚度，提出理論依據和優選范圍.