多彈協同微分對策制導律研究

郭志強,周紹磊

(海軍航空大學， 山東 煙臺 264001)

近年來，針對可以利用電磁干擾、假目標欺騙和大機動規避等手段的目標攔截問題引起了制導學者的重視[1-2]。由于微分對策制導律[3-8]在制導過程中不需對目標的機動規律作任何假設，只需考慮目標的機動能力，因而可使目標機動對制導精度的影響降到最小。本文根據多個攔截彈協同攔截單個機動目標的對策模型和制導要求，基于微分對策理論提出了一種協同制導律，該制導律選用了適用于所有對策參與者的性能指標，不需事先選擇相關的權值[9]，避免了對非連續性能指標泛函的處理。

1 運動模型及其簡化

1.1 非線性運動模型

本文考慮多個攔截彈協同攔截一個機動目標進行到末制導階段時的情況，并在制導律的推導過程中做出以下假設：

1) 攔截彈和目標均具有理想動力學特性，且在運動中均可視為質點；

2) 攔截彈和目標的速度均為常值，且其相對運動可在初始視線方向附近線性化；

3) 重力因素可忽略，且攔截彈和目標的制導問題可以在俯仰平面和偏航平面內解耦。

m個攔截彈與單個目標的平面相對運動關系如圖1所示，圖中XI-OI-YI表示慣性坐標系，Mi表示第i(i=1,2,…,m)個攔截彈，T表示目標。V、a和γ分別表示速度、法向加速度和航向角，變量的下標i和T分別相應于攔截彈Mi和目標T，LOSi0表示攔截彈Mi與目標之間的初始視線，λi0(λi)表示攔截彈Mi與目標之間的初始視線角(視線角)。

根據圖1所示的相對運動關系，可得極坐標下各攔截彈與目標的相對運動方程為

(1)

每個對策參與者各自的動力學方程可表示為

(2)

式中：xj=[xj1xj2…xjnj]T表示每個對策參與者的內部狀態向量；uj為其控制指令，根據假設1)有aj=uj；各自狀態向量的維數為dim(xj)=nj。

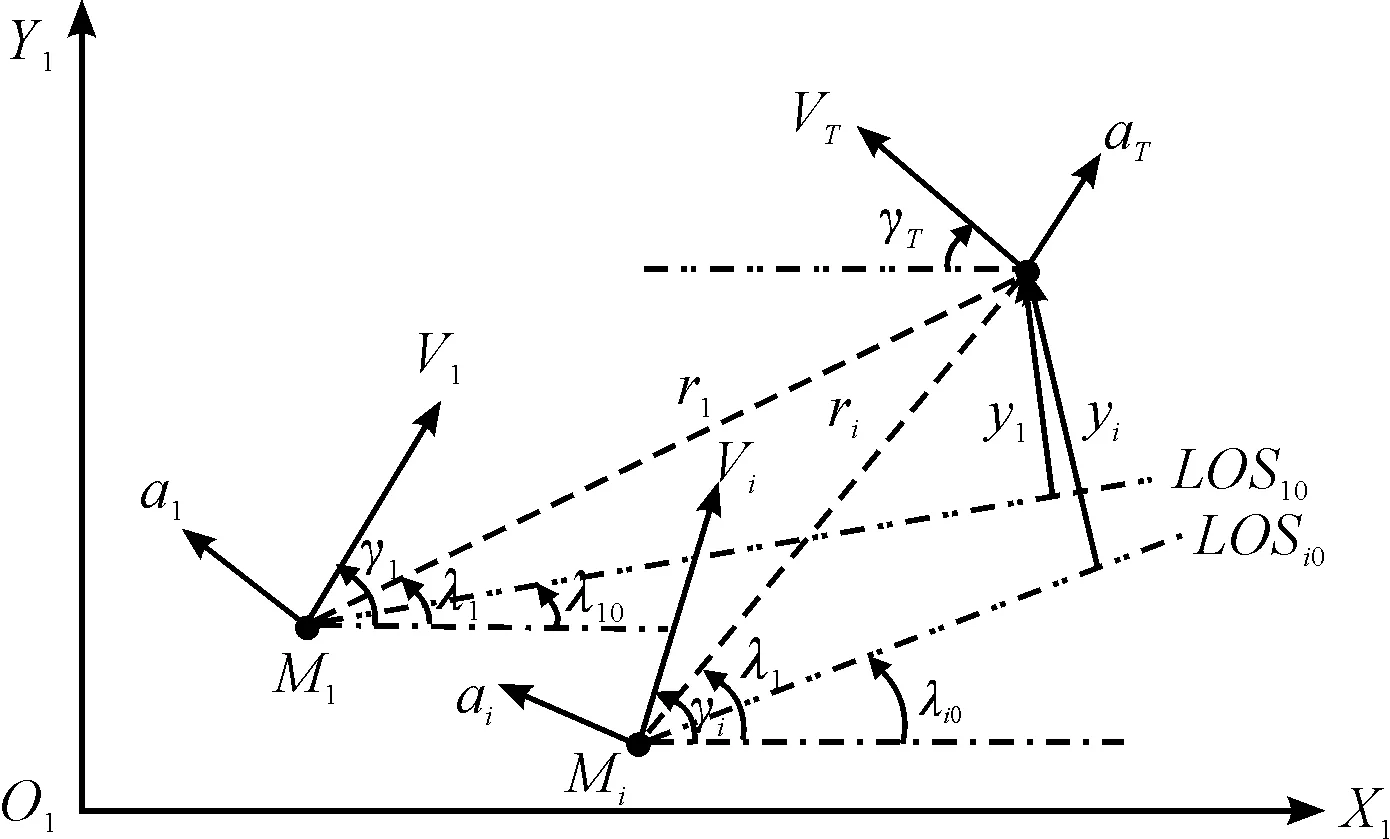
圖1 攔截彈-目標的平面相對運動關系

1.2 系統線性化

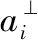
(3)

(4)

將對策各方所組成系統的狀態向量表示為

(5)

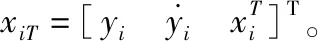
(6)

將式(6)寫成矢量形式則有

(7)

式中：A、B和C為適當的矩陣。

1.3 系統降階

由系統運動方程可以看出，系統維數

dim(x)=n1+…+nm+nT+2m

(8)

顯然，當系統維數龐大時對問題進行求解是十分繁瑣的。為了對系統進行降階，通過變換引入新的變量——零控脫靶量Zi(t)

Zi(t)=DiΦ(tfi,t)x(t)

(9)

式中：t為當前時刻，Φ(tfi,t)為系統狀態轉移矩陣，tfi為攔截彈Mi的終端攔截時刻。矩陣Di稱為狀態提取矩陣，其形式如下

(10)

攔截彈的終端攔截時間可近似表示為

(11)

在這里本文將對策結束時間定義為

tf=min{tf1,tf2,…,tfm}

(12)

新引入的零控脫靶量組成的向量可表示為

(13)

將其作為新的系統狀態向量，則系統維數可降至dimZ(t)=m。

對零控脫靶量求關于時間的導數可得

(14)

1.4 性能指標泛函

微分對策性能指標的選取主要有兩種類型，一種是直接采用零控脫靶量作為性能指標的范數型微分對策，另一種是采用線性二次型的性能指標。由于采用范數型微分對策所得到的制導律為“bang-bang”型控制律，不能充分發揮中間控制能量的最優性[10]，本文則根據零控脫靶量，為每個對策參與者選擇共同的二次型性能指標泛函如下

(15)

其中，αi、βi均為非負系數。αi表示對攔截彈脫靶量的約束，當αi→∞時表示攔截彈將獲得理想攔截對策(即終端脫靶量為零)；βi表示對攔截彈控制能量的約束。此時攔截彈與目標構成了線性二次型微分對策，攔截彈之間采取協同機動使性能指標J極小(也即使脫靶量極小的同時希望使所消耗的能量最小)，而目標則努力使性能指標J達到極大。

2 制導律設計

為簡單計，下面將針對兩個攔截彈協同攔截單個機動目標的情況進行分析，此時對策變為最簡單的情形——二對一追逃微分對策。

性能指標可寫為

(16)

該最優問題的哈密頓函數為

(17)

根據最優控制理論可得系統的伴隨狀態

λ1(t)=α1Z1(tf);λ2(t)=α2Z2(tf)

(18)

在對策過程中，參與對策的各方采取機動，使得下式成立

(19)

則根據控制方程

(20)

可得三者的開環最優控制為

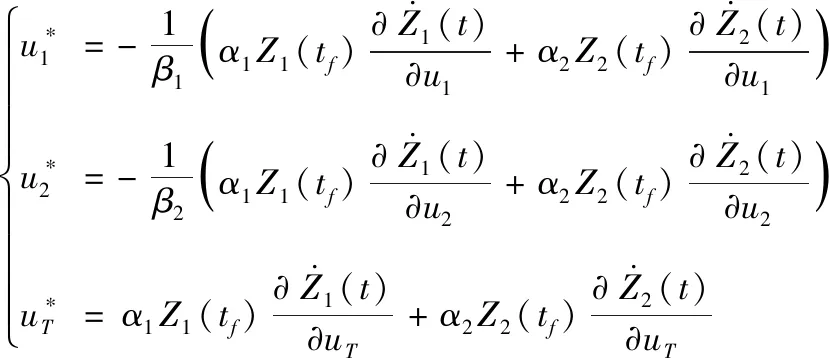
(21)

又由式(9)、式(10)可得零控脫靶量及其導數分別為

(22)

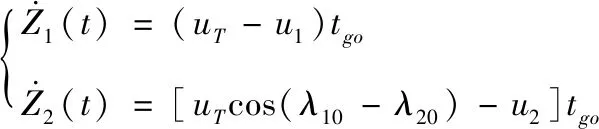
(23)

將式(23)代入式(21)可得

(24)

將式(24)代入式(23)，并分別從t到tf積分可得兩個耦合的方程，解之可得

(25)

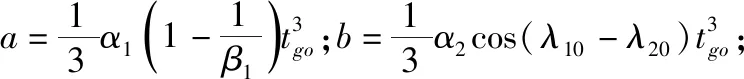
將式(25)代入式(24)，可得相應的閉環最優解為

(26)

其中

(27)

式中：Δ=(1-a)(1-d)-bc。容易看出，該微分對策問題的鞍點存在的充分條件為Δ≠0。

對于式(22)，根據小偏差假設則有

(28)

對上式求關于時間的導數后再代入式(22)可得

(29)

至此，式(26)所示的協同微分對策制導律設計完畢。本文通過為每個對策參與者選取共同的性能指標，有效避免了對分段連續性能指標泛函的處理，無需在制導律的初始階段選取較多的權值，得出了適合在線應用的制導律。

3 仿真分析

本節針對兩個攔截彈迎擊攔截單個大機動目標的情況對所設計的制導律進行仿真分析。仿真參數值如表1所示。

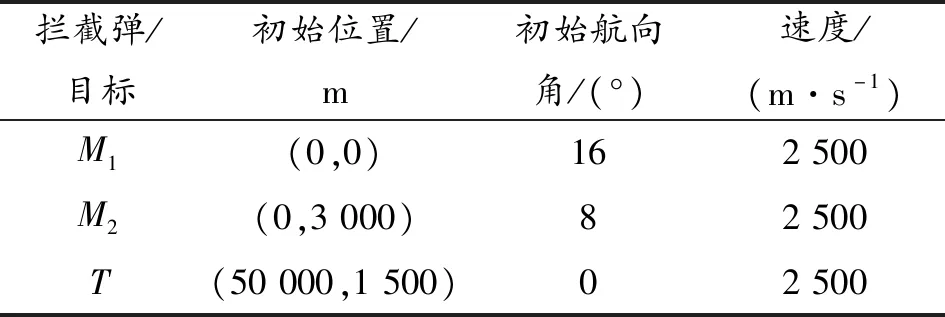
表1 仿真參數值

兩枚攔截彈采用本文提出的制導律協同攔截單個目標，仿真過程的有關系數取為α1=α2=108，β1=β2=2，仿真結果如圖2～圖5所示。

由圖2和圖3表明，利用本文所設計的制導律，攔截彈M2在攔截彈M1的協同配合下首先命中目標。由于本文及文獻[10]的制導方法均非時間上的協同制導，均未對制導時間做約束，故在對策結束時攔截彈M1與目標之間尚有一定距離，但這一距離并非其最終的脫靶量。

圖4表明，當攔截彈和目標均采用最優機動策略時，攔截彈可以以較低的加速度需求完成攔截任務(a1max≈47 m/s2，a2max≈58 m/s2，aTmax≈206 m/s2)，這說明通過采用本文制導律，攔截彈以較低的機動通過協同配合完成對高機動目標的攔截。

下面在表1給出的參數條件下，對兩枚攔截彈采用文獻[10]提出的CLQDG協同制導律的情況進行分析。仿真中CLQDG方法的相關參數選取為α=105，αE=105，該方法中權重系數k的取值為0.5，其結果如圖5-圖7所示。

圖5和圖6表明，在CLQDG方法中攔截彈M2率先命中目標。圖7為采用CLQDG制導律時攔截彈和目標的控制指令(a1max≈157 m/s2，a2max≈151 m/s2，aTmax≈295 m/s2)。

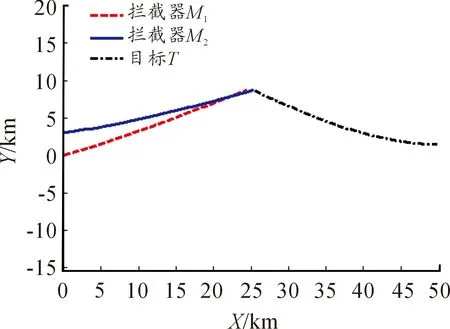
圖2 攔截彈與目標的運動軌跡

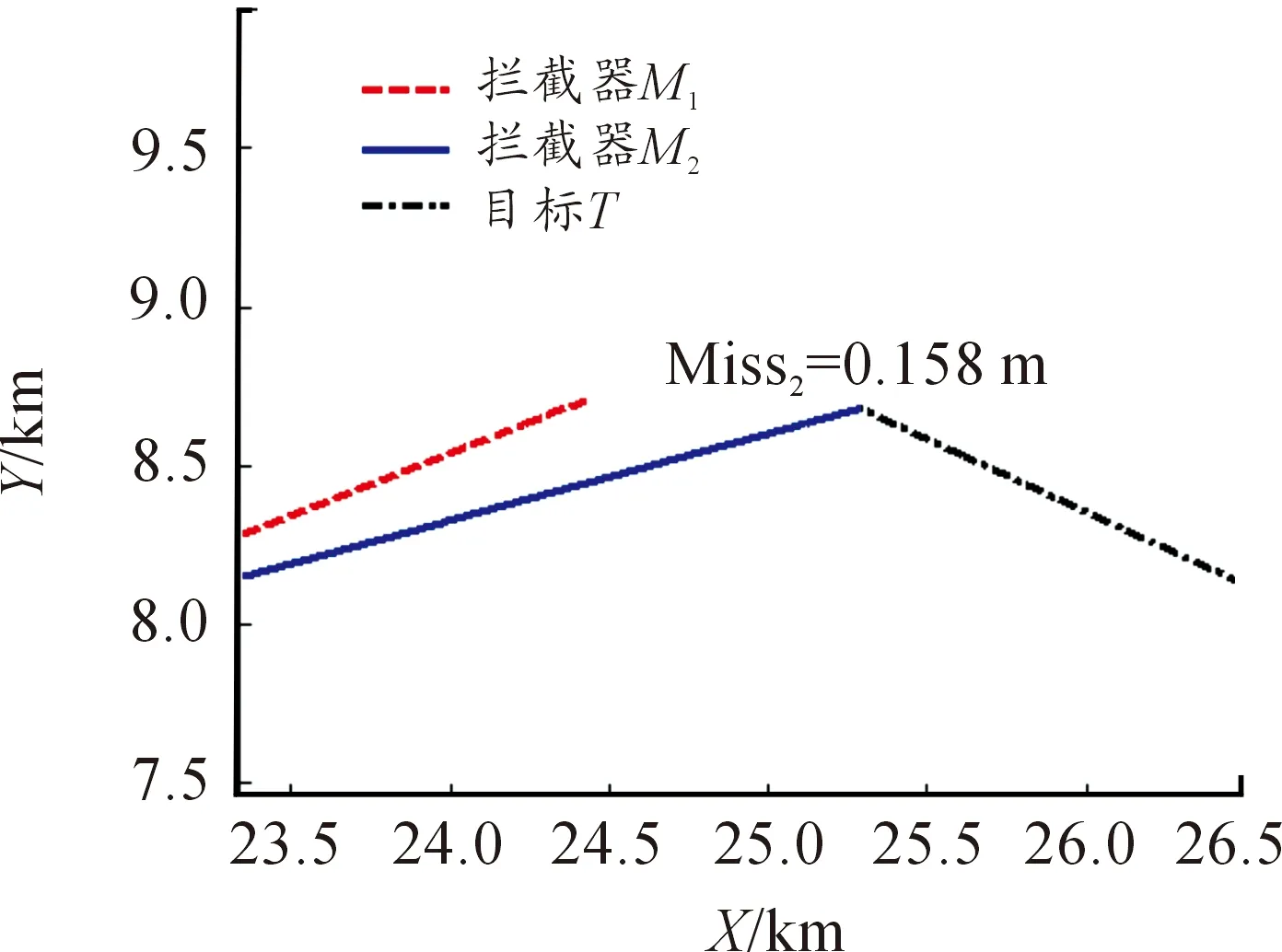
圖3 攔截彈與目標的運動軌跡(放大圖)

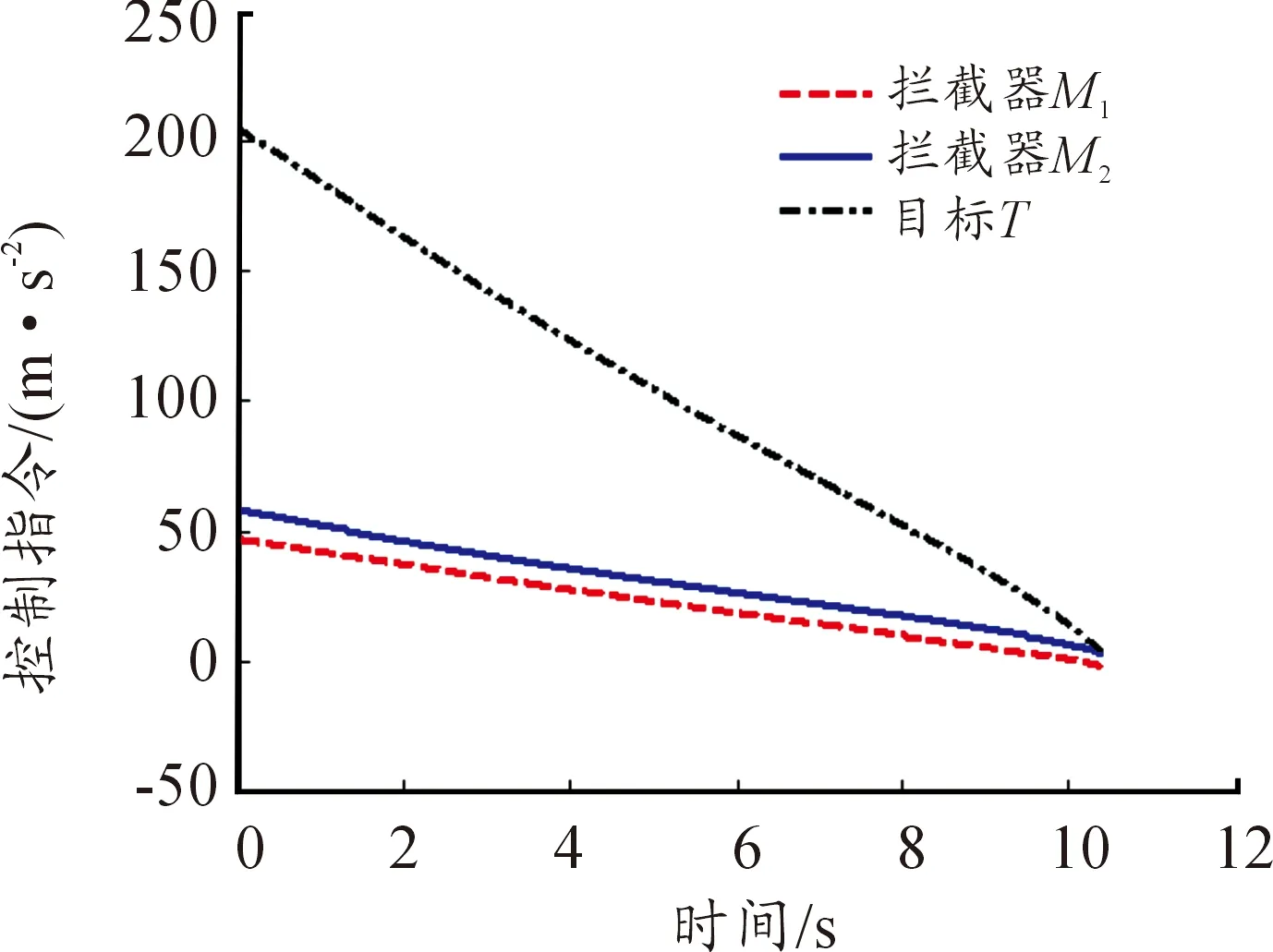
圖4 攔截彈與目標的控制指令

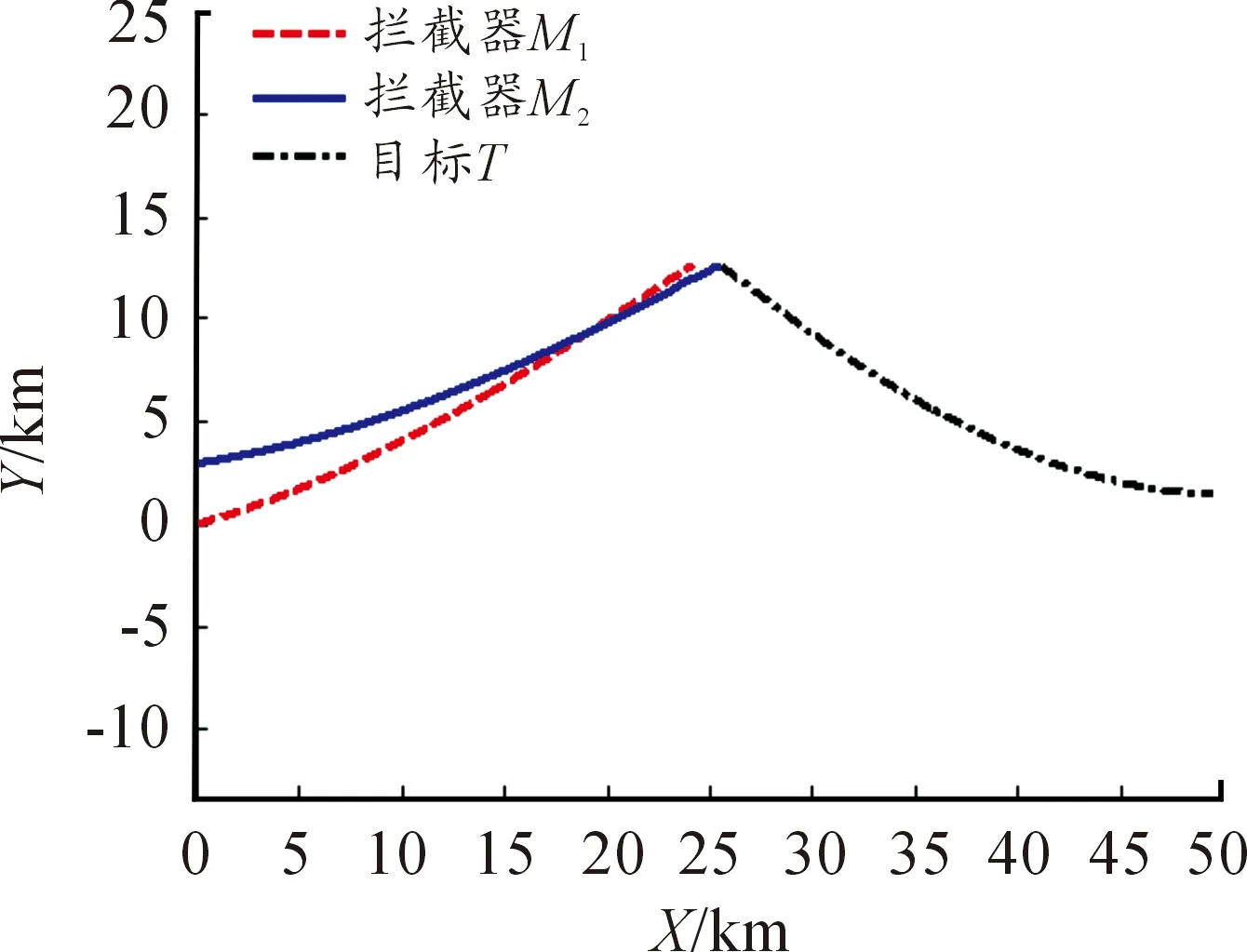
圖5 攔截彈與目標的運動軌跡-CLQDG

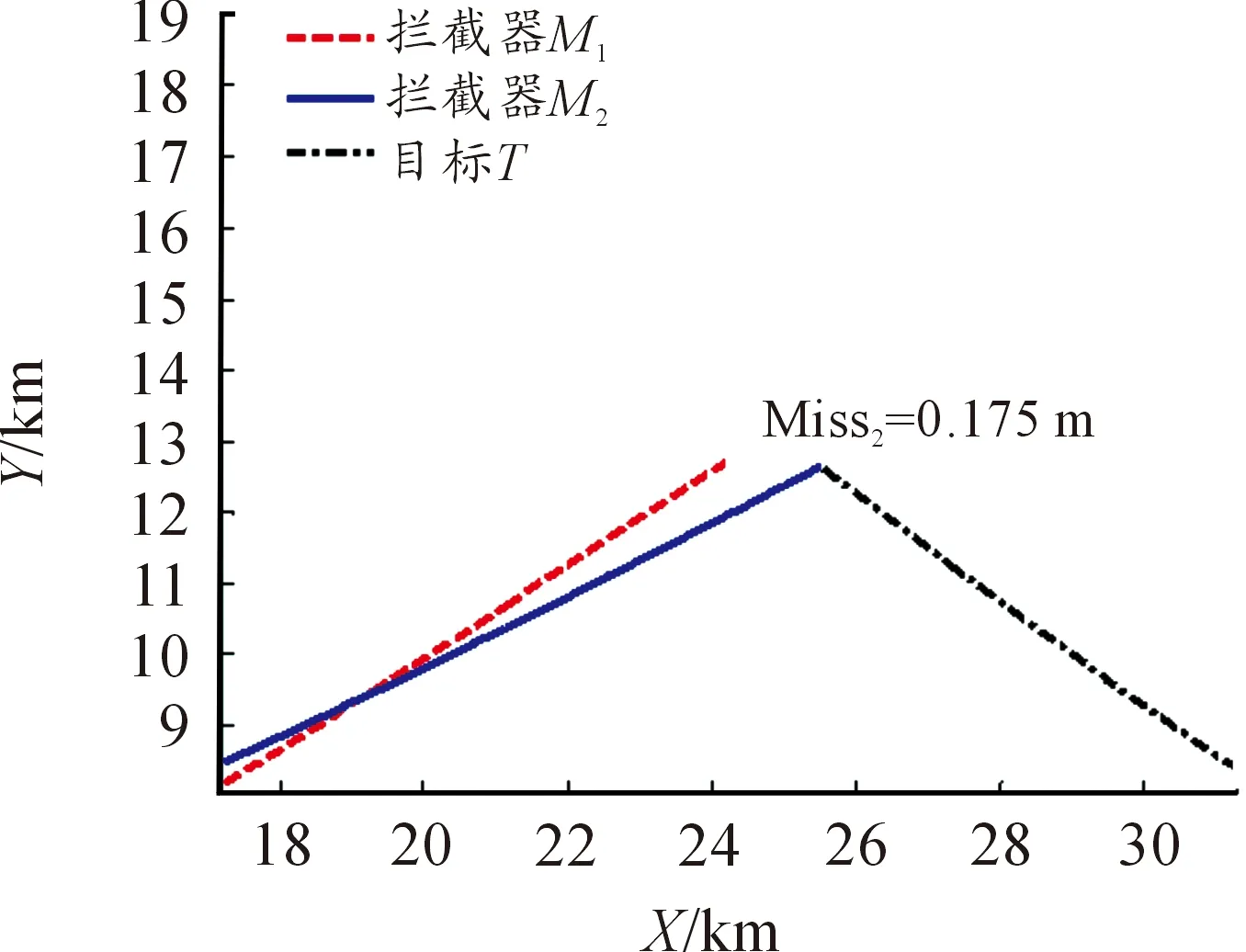
圖6 攔截彈與目標的運動軌跡-CLQDG (放大圖)

由以上仿真結果可以看出，采用兩種制導方法均能對目標進行攔截，但本文所提方法不涉及對分段函數的處理，而且攔截彈完成攔截所需的加速度需求減小，從而降低了對攔截彈的機動性要求，實現了對高機動目標的攔截。

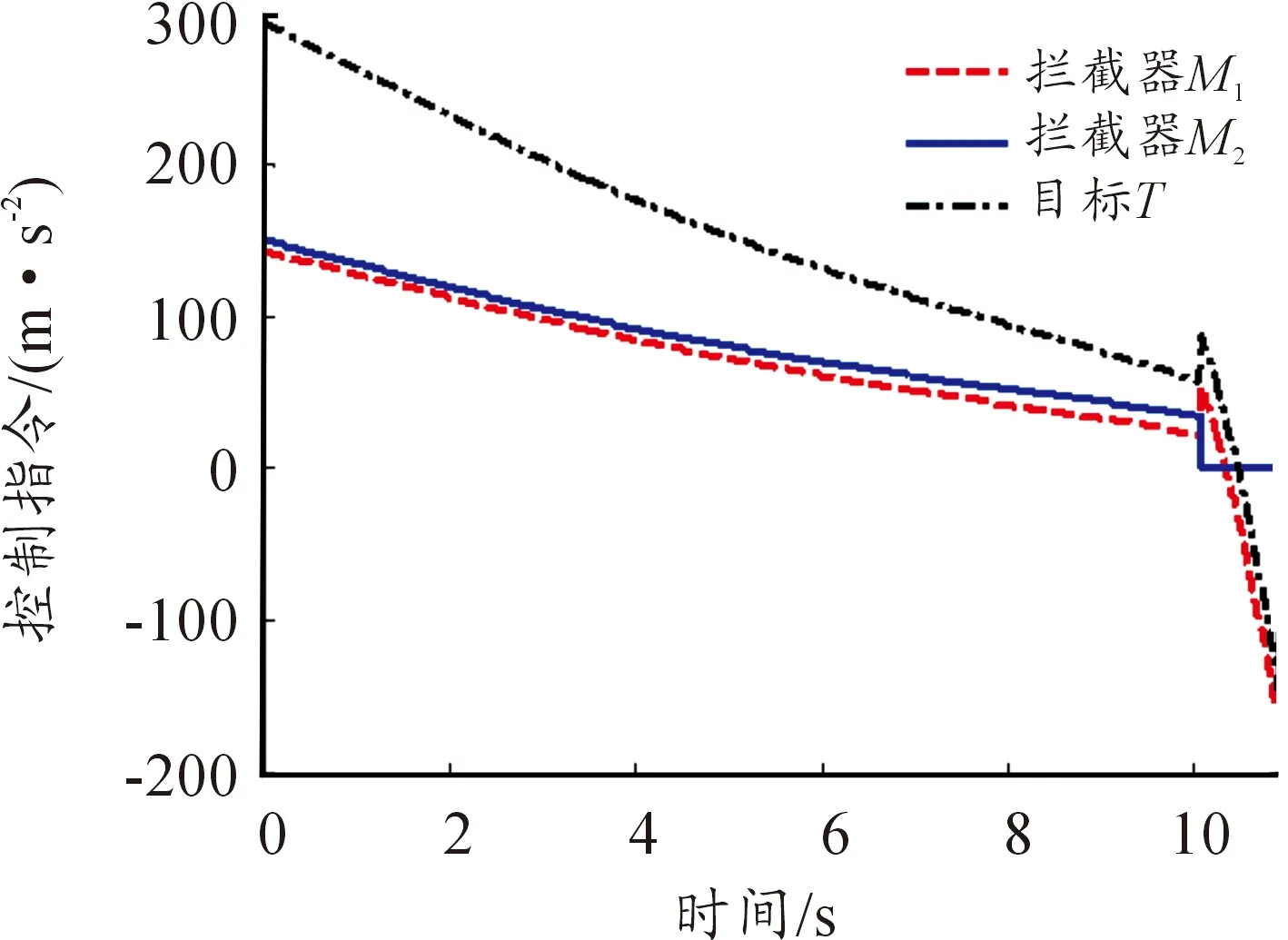
圖7 攔截彈與目標的控制指令-CLQDG

4 結論

考慮到當追逃雙方分別采用不同的性能指標時，要涉及到分段函數的處理以及相關參數的事先選取，為了避免這些問題，本文基于微分對策理論，選取了適用于所有對策參與者的性能指標，進一步推導出對策雙方的閉環最優制導策略。在對策過程中，各攔截彈在追求自身脫靶量最小的同時，采取協同機動以減小其他攔截彈的脫靶量，通過仿真分析表明了本文所提制導律的有效性。