求解線性規劃的一種新的原始對偶內點法

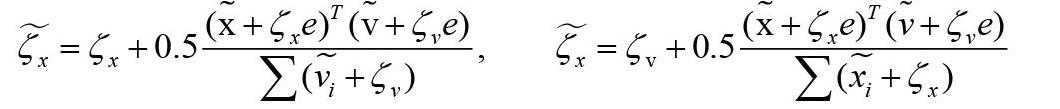
摘? 要：該文在線性規劃問題的目標函數中增加二次項，并提出了一種新的原始對偶內點法解該問題。該方法對增加二次項后的問題的KKT條件中的變量做代換。對新變量做凸松弛保證新變量元素全為正值。對互補性條件做凸松弛，互補性條件右側每一個分量為依賴于當前迭代點相應分量的松弛。數值實驗表明，該文算法對解決線性規劃問題是有效的。

關鍵詞：線性規劃? 新的原始對偶內點法? KKT? 條件? 互補性條件

中圖分類號：O221.1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1672-3791（2019）04（b）-0168-03

標準的線性規劃問題：

其中行滿秩。（P）的對偶問題是：

其中分別是等式和不等式約束的拉格朗日乘子。

Magasarian等[1]在（P）中加擾動項：

其中。若（1）有唯一解，則存在充分小，當時（1）的解是（P）的解。Gill等[2]在（P）中加擾動項：

其中δ>0。Gill等用原始對偶障礙函數法解（2）。Wang等[8]在（P）中加擾動項：

其中Xk是當前迭代點。Wang等[8]用鄰近增廣拉格朗日同倫法解（3）。

Darvary[7]用加權路徑跟蹤內點算法求解線性規劃問題。內點法中Xz=τe互補性條件等于常向量τ∈R+，Darvary算法中Xz=w，w∈R+n不是常向量。

該文在線性規劃問題的目標函數中增加二次項。受Darvary的啟發，提出一種新的原始對偶內點法。互補性條件右側每一個分量為依賴于當前迭代點相應分量的松弛。數值實驗表明，該文算法對解決線性規劃問題是有效的。

該文結構如下：第一節提出求解線性規劃的新模型并給出了相應的算法：第二章為數值實驗;最后一部分是結束語及參考文獻。

1? 原始對偶正則內點算法

原始對偶問題（P）-（D）的KKT條件是：

原始對偶問題（P）-（D）的嚴格可行集是：

（P）的目標函數進行松弛：

（5）的對偶問題是：

其中，原始對偶問題（5）（6）的KKT條件是：

其中是元素全為1的列向量。令，則：

其中V=diag（v）。對互補性條件和變量v做松弛：

令，上述方程變為：

通過求解方程（8）的牛頓方程來找搜索方向

第三行左乘-Xk-1加到第一行得到：

△v可以通過下面的式子得到：

為了阻止迭代點太接近非負邊界，路徑追蹤算法要求每一個迭代點都滿足中心路徑的無窮范數鄰域：

同樣為了保證新算法產生的迭代點遠離非負邊界，我們算法的中心路徑的鄰域定義為：

其中0<γ<1是給定常數。該文按如下方式產生下一次迭代點Wk+1（Xk+1，yk+1，vk+1）。通過（9）和（10）計算牛頓步，步長滿足：

下面給出新的原始對偶內點算法。

算法 1

步驟1：初始正則參數，參數0<γ<1，停止ε>0準則。選擇初始點保證，，k=0。

步驟2：若，收斂。

步驟3：通過方程（8）和（9）計算牛頓步。

步驟4：計算滿足

0且，的最大ak。這里。

步驟5：令

，選取擾動系數

。返回步驟2。

假設：

（1）原始對偶問題的最優解*有界;

（2）非空。

由對偶理論可知為原問題（P）和對偶問題（D）的解的充要條件是式（11）成立。因為{ηk}是下降序列，當η→0且*是有界值時，方程組的解將分別收斂于（P）和（D）的最優解。

定理1? 算法1產生序列且有界。當η→0時，方程組的解是原始對偶問題（P）-（D）的最優解。

2? 數值實驗

該章所有的數值測試都是在MATLAB-R2012a中進行的，運行環境為聯想電腦 （Intel（R） Core＼＼（TM） i5-3230M CPU 2.60GHz，4.00GB）。

數值實驗的算例來自Netlib測試集。用算法1計算Netlib測試集。我們給出了算法1的實驗結果，并對實驗結果進行分析。

對于大部分問題來說，嚴格初始可行點很難找到。找嚴格初始可行點通常要對問題進行變形，但是對問題進行變形往往會讓問題變得更難求解。因此我們在實際計算中選取不可行初始點。不可行初始點僅要求X0>0，Z0>0。不可行初始點遵循Methora線性規劃初始點選取規則：

選取。我們得到：

因此初始點為和。文中表明生成的初始點滿足X0>0，Z0>0。

Friedlander等提出了新的正則化方法：

文中證明了當ρ、δ取固定常數時算法收斂并且該算法在實際計算中也沒有要求滿足中心路徑。該文在實際計算中使用方程（11）求方向ρ=δ=10-10。

我們選取算法1的終止條件是：

其中ε=10-5。當η→0時，v→z第三個條件就變成了對原始對偶問題的對偶間隙的限制。

表1表示算法1在Netlib測試集上的計算結果。第一列是Netlib測試問題的名稱，第二列是問題的維數，第三列是等式約束的個數，第四列是Netlib測試集網站提供的最優值，第五列是算法1的迭代次數，第六列是算法1的最優值。由表1可以看出算法1對解決線性規劃問題是有效的，且對每一個算例算法1的計算結果在一定誤差范圍內。

3? 結語

該文在線性規劃問題的目標函數中增加二次項并提出了一種新的原始對偶內點算法。受到加權路徑追蹤算法的啟發，對增加二次項后的問題的KKT條件中的變量做變量代換。對變量代換后的KKT條件中的新變量做凸松弛保證新變量元素全為正值。對互補性條件做凸松弛，互補性條件右側每一個分量由相同數值松弛變為依賴于當前迭代點相應分量的松弛。數值實驗表明，該文算法對解決線性規劃問題是有效的，但其收斂速度還有待研究。

參考文獻

[1] Mangasarian OL.Iterative Solution of Linear Programs[J].SIAM Journal on Numerical Analysis， 1979， 18（18）：606-614.

[2] Saunders M， Tomlin J. A.Solving regularized linear programs using barrier methods and KKT systems[D].SOL Report 96-4， Dept. of EESOR， Stanford University，1996.

[3] Friedlander MP.Orban DA primal-dual regularized interior-point method for convex quadratic programs[J].Mathematical Programming Computation，2012，4（1）：71-107.

[4] Chen S，Donoho DL，Saunders MA.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing，1998，20（1）：33-61.

①通訊作者：張溪（1992，11—），女，漢族，河北辛集人，碩士研究生，研究方向：運籌與優化，E-mail：2645816447@qq.com。