基于Pareto最優均衡理論的商用車路徑跟蹤與抗側傾協同控制研究*

李玉善，遲元欣，季學武，劉玉龍，武 健

（1.山東科技大學交通學院，青島 266590； 2.清華大學，汽車安全與節能國家重點實驗室，北京 100084）

前言

智能車輛因為具有降低駕駛員工作負擔、提高汽車安全性等優點得到了快速發展，智能商用車相比于乘用車，由于行駛環境和運營方式的特點，在推廣上顯示出明顯優勢，已經開始吸引人們的關注［1-2］。智能車輛通過自動轉向控制實現對期望路徑的跟蹤，稱為路徑跟蹤橫向控制［3］，而商用車質心位置較高，側翻閾值和側傾穩定性較低，橫向與側傾動力學相互耦合，轉向過程中的側翻事故屢屢發生。據統計，20%的商用車事故由側傾和橫向失穩導致，其中66%發生在轉向過程中［4］，商用車的抗側傾控制吸引了廣泛的關注。

目前，關于商用車抗側傾控制的研究主要集中于主動抗側傾裝置及其控制，如差動制動［5］、主動抗側傾桿［6］、主動轉向以及差動制動和主動抗側傾桿之間的聯合控制［7］，在控制方法上，針對模型參數的不確定性，張志勇等人基于線性矩陣不等式的魯棒控制理論，提出了基于觀測器的抗側傾輸出反饋控制方法［8］；Vu等人基于H∞控制理論設計了對車速和簧載質量魯棒的主動防側傾控制器［9］；Gaspar等人考慮車速時變特性，運用線性變參數（LPV）法進行了主動防傾桿和主動制動的聯合控制［10］；Boada等人提出了一種基于神經網絡的強化學習算法來提高商用車的側傾穩定性［11］；靳立強等人基于零力矩點位置計算了側翻時間，當側翻時間小于設定門限值時，基于模糊PID控制策略對不同車輪施加制動力矩［12］。在這些控制器設計過程中，將車輪轉角視為系統外界不確定擾動輸入，基于相應抗側傾性能指標設計抗側傾控制器，并求得在前輪不確定擾動輸入下保證車輛側傾穩定性的控制輸入。而實際上，車輛的橫向動力學和側傾動力學通過橫向-側傾慣性積相互耦合，在智能商用車上的表現為車輛的側傾動力學受橫向控制系統轉角輸入的影響，同時橫向動力學也受抗側傾系統控制輸入的影響，僅將二者互為分散地設計橫向與抗側傾控制策略將忽略二者之間的相互作用。

動態博弈理論在處理多目標優化、多參與者存在相互交互的復雜系統問題上具有潛在應用［13-15］，針對商用車路徑跟蹤橫向-側傾控制過程中，轉向子系統與抗側傾子系統等多個子系統之間交聯耦合又相互影響，各子系統控制輸入彼此互相影響又共同對車輛橫擺-側傾動力學產生作用，因此，基于動態博弈理論設計商用車橫向-側傾穩定性控制器具有明顯的優勢。

本文中針對商用車路徑跟蹤橫向與抗側傾控制，提出了一種基于動態Pareto最優均衡的協同式最優控制策略，在路徑跟蹤-抗側傾全局性能指標優化的基礎上，橫向控制器與抗側傾控制器充分考慮彼此的控制輸入，得到滿足Pareto最優均衡的控制策略。為此，首先建立路徑跟蹤橫向與抗側傾控制智能車-道路閉環模型。其次基于最優控制理論，設計了分散式橫向與抗側傾控制器作為對比，基于合作式閉環Pareto均衡理論設計了橫向-抗側傾協同式最優控制器。最后進行仿真對比，結果表明，所設計的協同式最優控制策略能夠降低系統橫向-側傾動力學之間的相互影響，在保證路徑跟蹤精度的同時有效提高了商用車側傾和橫向穩定性。

1 智能商用車-道路閉環模型

1.1 商用車橫擺-側傾耦合模型

為描述車輛轉向輸入對側傾和操穩的響應，Segal最早建立了包含橫向、橫擺和側傾運動的線性車輛3自由度模型［16］，為研究主動防側傾裝置，Tan等人建立了包含抗側傾執行機構模型的車輛橫擺-側傾耦合模型［17］。主動轉向、差動制動等防側傾方法需要對前輪進行直接的橫向或縱向控制，會對路徑跟蹤橫向控制產生直接影響，因此本文中采用主動抗傾桿作為主動抗側傾裝置，建立抗側傾控制車輛模型，如圖1所示，將車輛分為簧載質量和前后非簧載質量3部分，僅考慮簧載質量的橫向、橫擺運動，以及簧載質量和前后非簧載質量繞車輛側傾軸線的轉動，建立簧載質量側傾、橫向、橫擺以及前后軸非簧載質量側傾動力學模型，如式（1）～式（5）所示，各符號詳細描述見表1。

圖1 商用車橫-擺-側傾耦合模型

表1 模型中的符號與描述

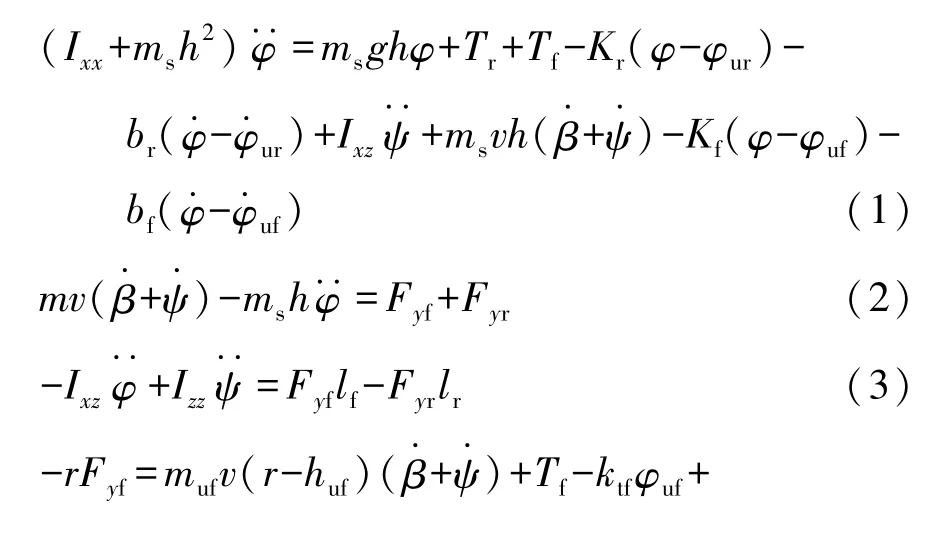
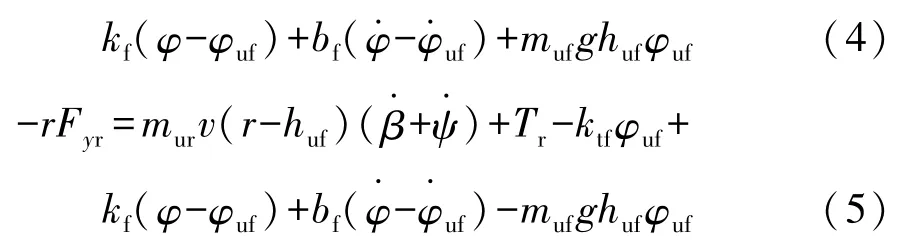
式中前后軸側向力Fyi可由前后軸等效側偏剛度表示為

在前后軸側偏剛度較小的情況下，前后軸等效側偏角可表示為

為了對路徑跟蹤的橫向跟蹤誤差進行表達，首先需要描述車輛的實時橫向位置和航向角，在車輛航向角很小的情況下，橫向位置可表示為

根據式（1）～式（8），建立用于路徑跟蹤橫向與抗側傾控制器設計的車輛狀態空間方程：

式中：x為系統狀態向量；u為系統輸入；y為系統輸出。

根據矩陣A，B，C，D，利用MATLAB函數c2d可得到車輛離散狀態方程：

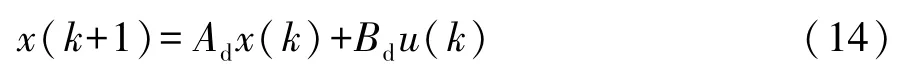
1.2 智能車-道路閉環模型

Sharp等人［18］通過將預瞄點信息與離散車輛狀態方程結合，得到多點預瞄路徑跟蹤模型，車輛前方的Np＋1個預瞄點的期望信息可通過道路移位寄存器矩陣表示為

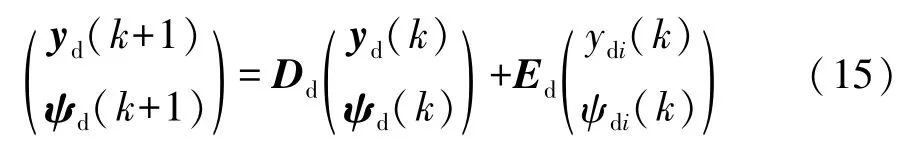
式中：yd為當前時刻車輛前方Np＋1個點的期望橫向位置yd0，yd1，yd2，…，ydNp-1，ydNp組 成的列向量；ydi為當前時刻輸入的預瞄點期望橫向位置；ψd為當前時刻車輛前方Np＋1個點的期望航向角 ψd0，ψd1，ψd2，…，ψdNp-1，ψdNp組成的列向量；ψdi為當前時刻輸入的預瞄點期望航向角；Dd為道路移位寄存器矩陣；Ed為道路輸入矩陣。Dd和Ed可表示為

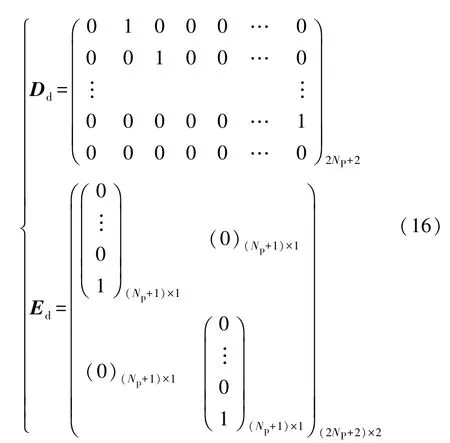
將道路預瞄信息模型增廣到式（14）車輛離散狀態方程中得到車輛-道路閉環模型：

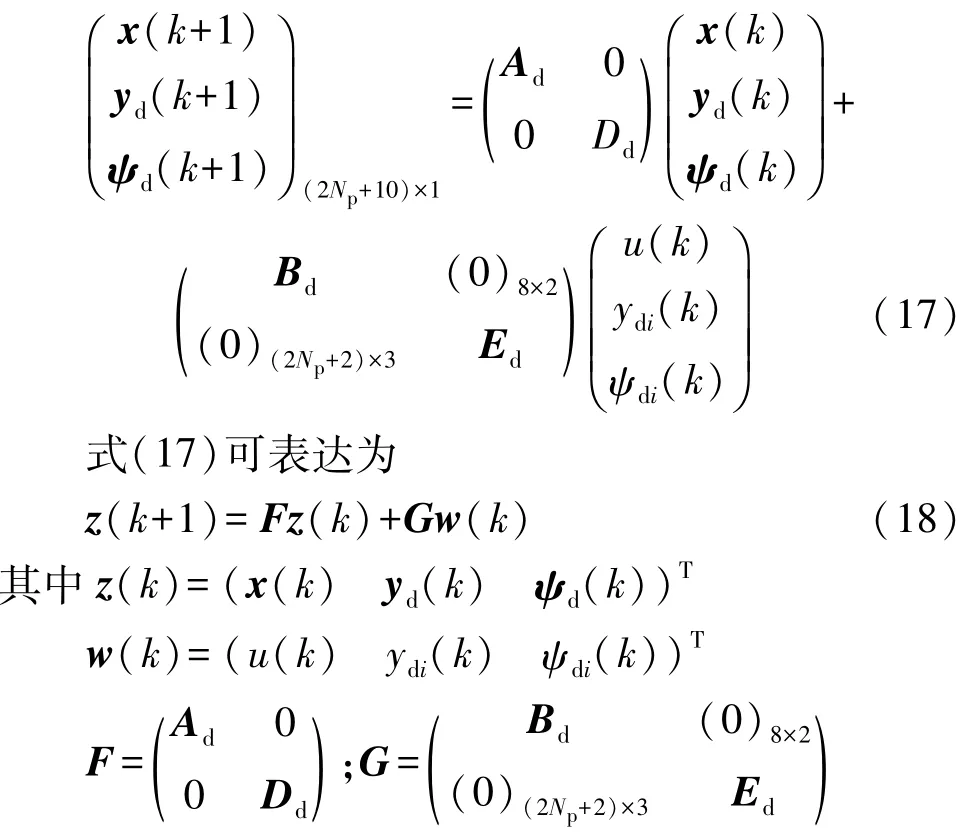
2 路徑跟蹤橫向控制與抗側傾控制策略設計

2.1 二次代價函數

2.1.1 路徑跟蹤橫向控制二次代價函數

選取預瞄點處的橫向位置誤差（y（k）-yd（k））與航向角誤差（ψ（k）-ψd（k））作為路徑跟蹤性能指標加權項，假設控制域為Nu步，則二次代價函數為

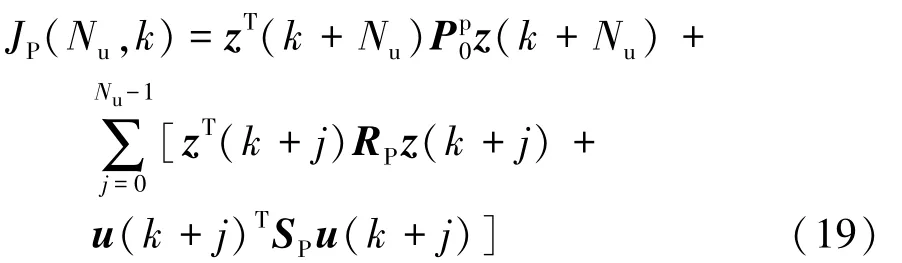
式中：RP為路徑跟蹤橫向控制性能指標加權矩陣；SP為輸入加權矩陣；為終端加權矩陣，通常為RP。

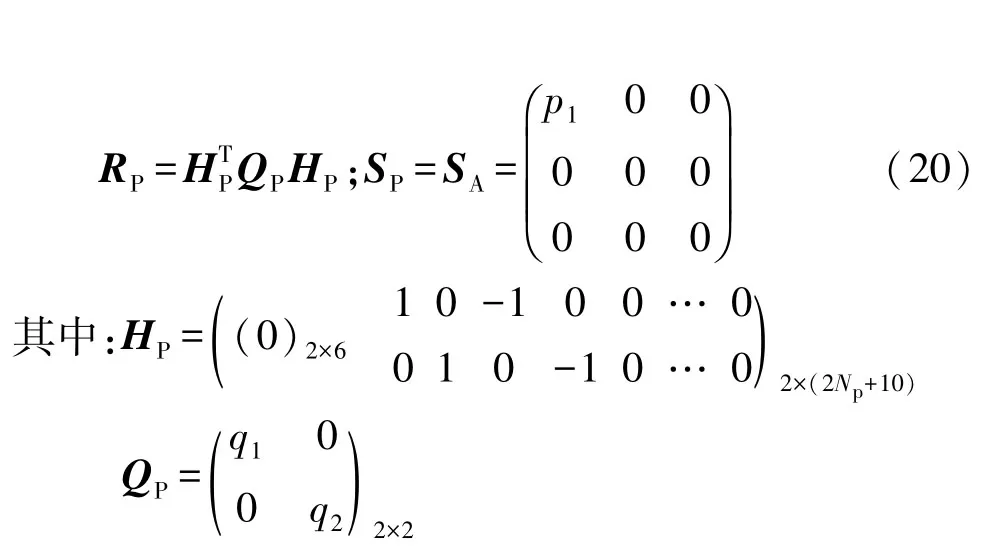
式中：q1和q2為性能指標加權系數；p1為輸入加權系數。

2.1.2 防側傾控制二次代價函數

選取簧載質量側傾角φ、前軸歸一化載荷轉移Rf、后軸歸一化載荷轉移Rr、簧載質量與前軸非簧載質量側傾角之差（φ-φuf）和簧載質量與后軸非簧載質量側傾角之差（φ-φur）作為主動抗側傾控制性能指標加權項，Rf和Rr如式（21）所示。

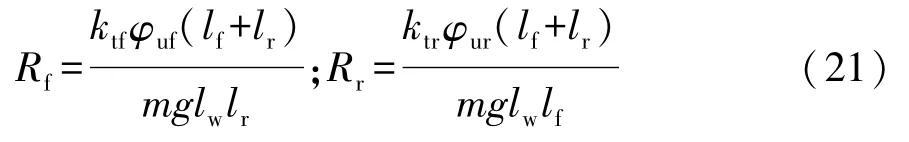
假設控制域為Nu步，則有限時域離散形式二次代價函數為

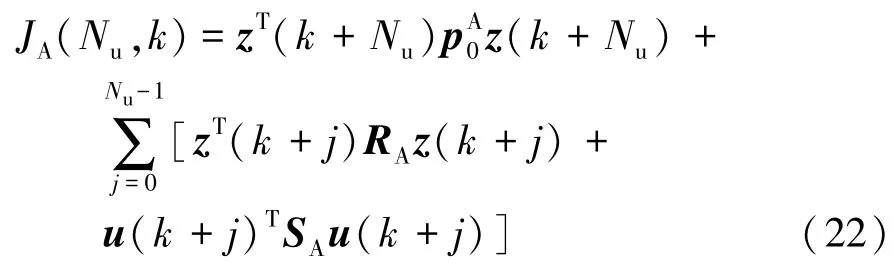
式中：RA為抗側傾控制性能指標加權矩陣；SA為輸入加權矩陣為終端加權矩陣，通常為RA。

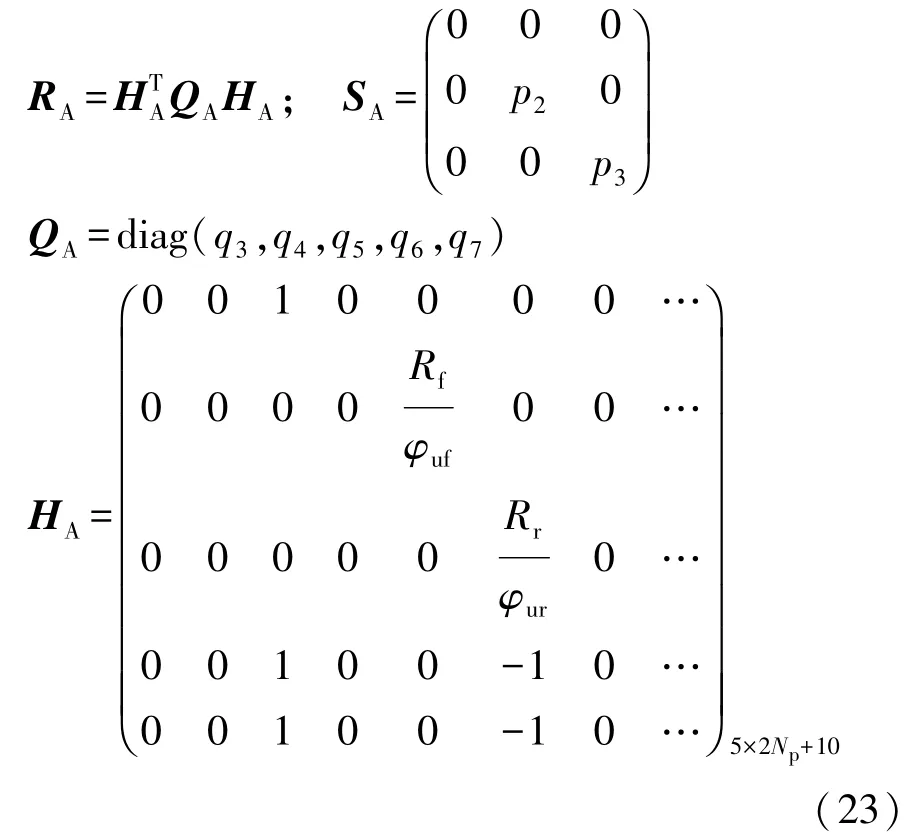
式中：q3～q7為性能指標加權系數；p2和p3為輸入加權系數。

2.2 分散式最優控制策略

車輛在進行自動橫向控制與抗側傾控制時，路徑跟蹤控制器和抗側傾控制器有各自的控制目標，最基本的控制方法是利用分散式最優控制將兩個控制器簡單組合，每個控制器根據線性二次型最優理論計算自己的控制律，而控制器間沒有交互，其控制框架如圖2所示。圖中，JP（Nu，k）和JA（Nu，k）如式（19）和式（22）所示。

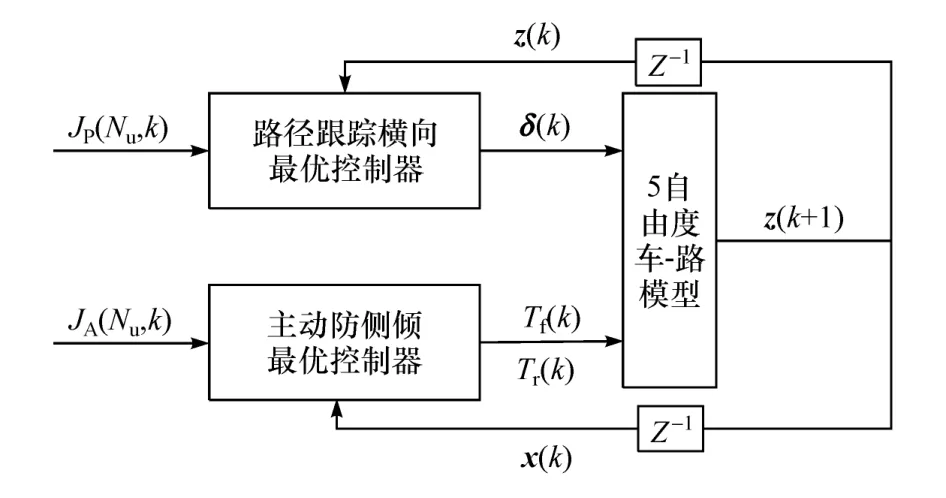
圖2 分散式最優控制框架

將式（19）與式（22）結合，得到分散式全局二次代價函數J（Nu，k）：

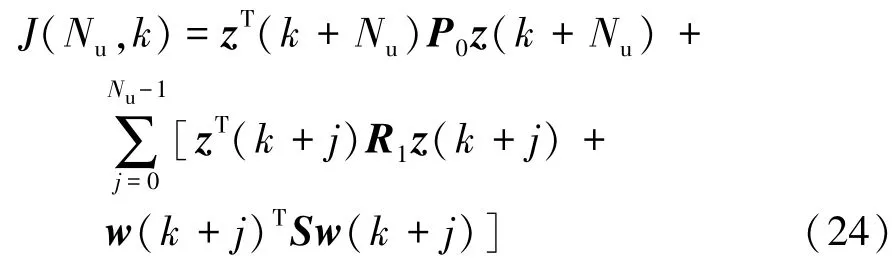
式中：R1為分散式全局性能指標加權矩陣；P0為終端加權矩陣；S為輸入加權矩陣，通常取P0=R1；z為狀態矢量。

Bitmead［19］指出，基于龐伽里特金原理求解離散時間線性二次型最優控制器，可從初始條件P0開始迭代差分形式的黎卡提方程，如式（25）所示。

十個吃客有九個會說，毛蟹炒年糕里的年糕最好吃。年糕浸滿了蟹味，包裹著醬汁，軟軟糯糯的，比蟹都要嗲，會吃的都要去挑年糕吃，受冷落的都是毛蟹。可我就不這么認為，我就是那十分之一，就是覺著蟹好吃。

在k時刻，控制域Nu內第j步最優輸入為

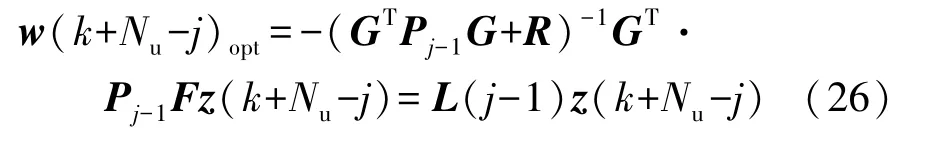
取k時刻所得控制序列的第一個輸入w（k）opt作為當前時刻的最優輸入，則線性時不變（LTI）系統的滾動時域二次型最優控制輸入為

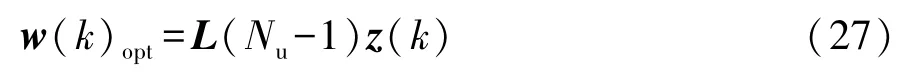
2.3 基于Pareto最優均衡的協同式控制策略

由圖2所示的控制結構可以看出，系統狀態z（k）同時受輸入 δf，Tf和Tr的影響，分散式最優控制中的每個最優控制器在計算最優控制策略時，忽略了另外一個控制器的控制目標和控制輸入，因而此時路徑跟蹤橫向控制器所計算的最優車輪轉角可能對防側傾控制目標產生不利影響，反之亦然。

Pareto均衡理論作為一種合作式博弈策略，在系統動態演化過程中，各控制參與者在進行控制決策時，不僅考慮自身的利益函數，還會考慮其他參與者的利益函數。為更好地減弱商用車橫向-側傾動力學的耦合，本文中基于Pareto均衡理論設計了協同式最優控制框架，如圖3所示。

圖3 基于Pareto均衡的交互共享式控制框架

這種控制框架中有兩條通道，兩個最優控制器之間彼此交互，分享各自的控制目標和控制輸入，路徑跟蹤橫向控制器和防側傾控制器同時將各自性能指標的線性加權之和作為自身的性能指標，如式（28）所示，根據此性能指標并同時考慮對方控制器的控制輸入來計算自身的最優控制策略，因此每個控制器不僅使自己的性能指標極小，還極小化自身控制輸入對另一性能指標影響，達到全局最優。

根據Pareto最優均衡理論，則式（19）和式（22）所示二次型目標函數為

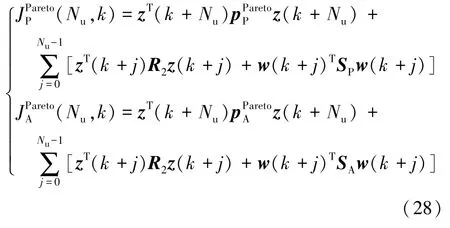
式中R2為Pareto最優全局性能指標加權矩陣，如式（29）所示。

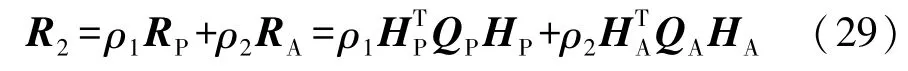
式中ρ1和ρ2為加權系數。為便于Pareto協同最優控制器的設計，將式（17）所示的智能車-道路閉環模型改寫為

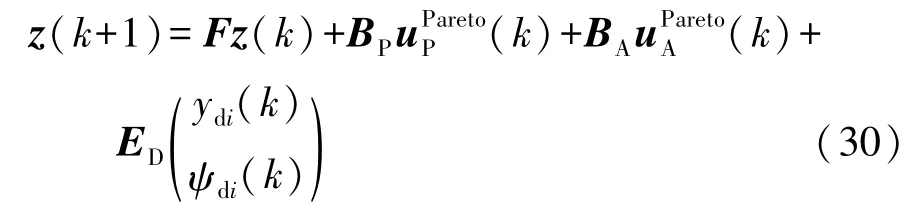
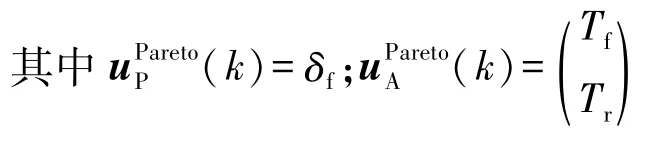
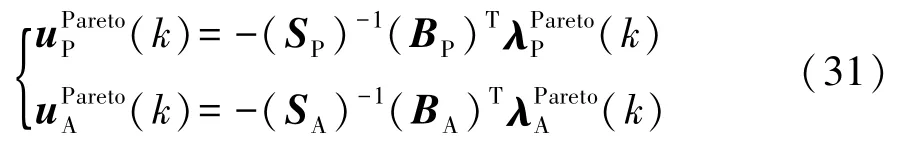
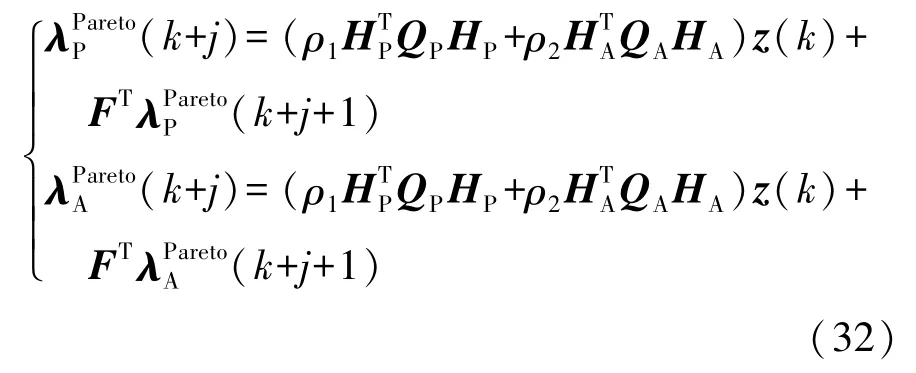
根據式（32）可得到協態變量與狀態變量之間的線性關系：

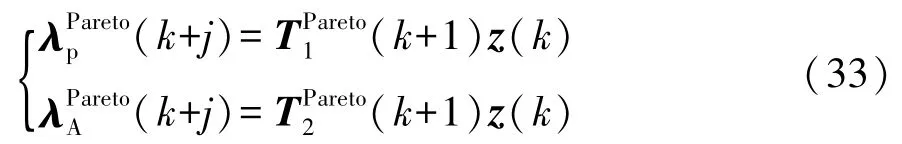
根據式（30）、式（32）和式（33），可得如下一組耦合黎卡提迭代方程：

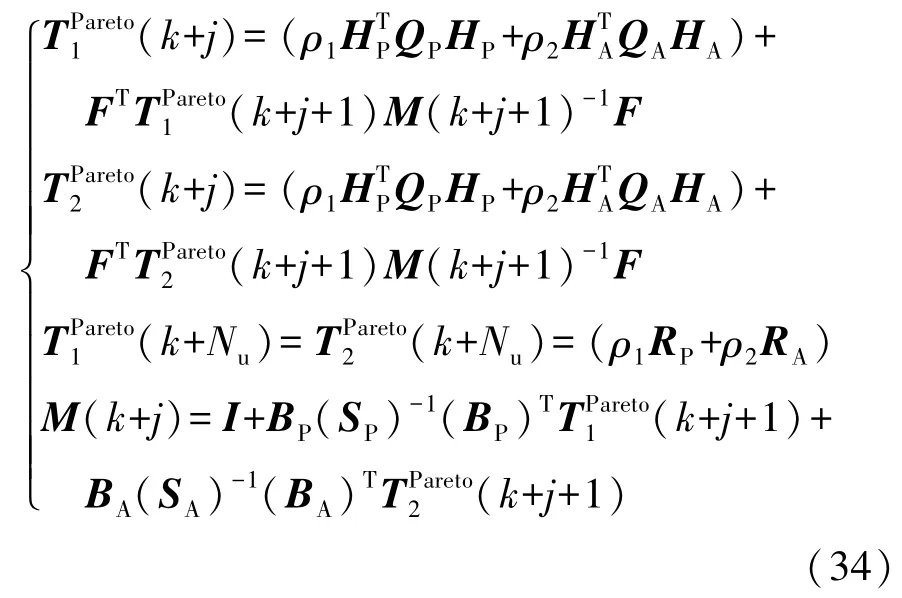
3 仿真與結果分析

本文中基于多點預瞄理論制定路徑跟蹤控制策略，并在此基礎上分別設計了分散式最優橫向-抗側傾控制策略、Pareto協同式最優橫向-抗側傾控制策略；為進一步說明控制結果，選取蛇形線作為期望路徑進行跟蹤，將所設計的兩種控制策略與單純路徑跟蹤時的控制策略進行對比，仿真驗證所提出的基于Pareto協同式最優控制策略的有效性。

歸一化載荷轉移能夠衡量車輛側傾穩定性，當歸一化載荷轉移超過1或-1時，車輛發生側翻，為了分析對側傾穩定性控制效果，選取3種控制方法下的前后軸歸一化載荷轉移進行比較，如圖4和圖5所示，圖中點劃線表示歸一化載荷轉移為-1。

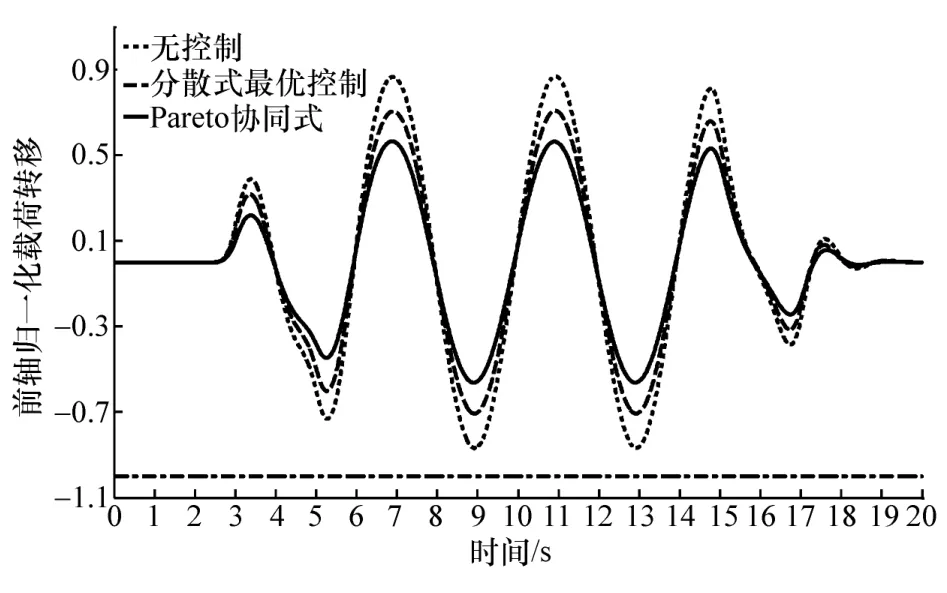
圖4 前軸歸一化載荷轉移

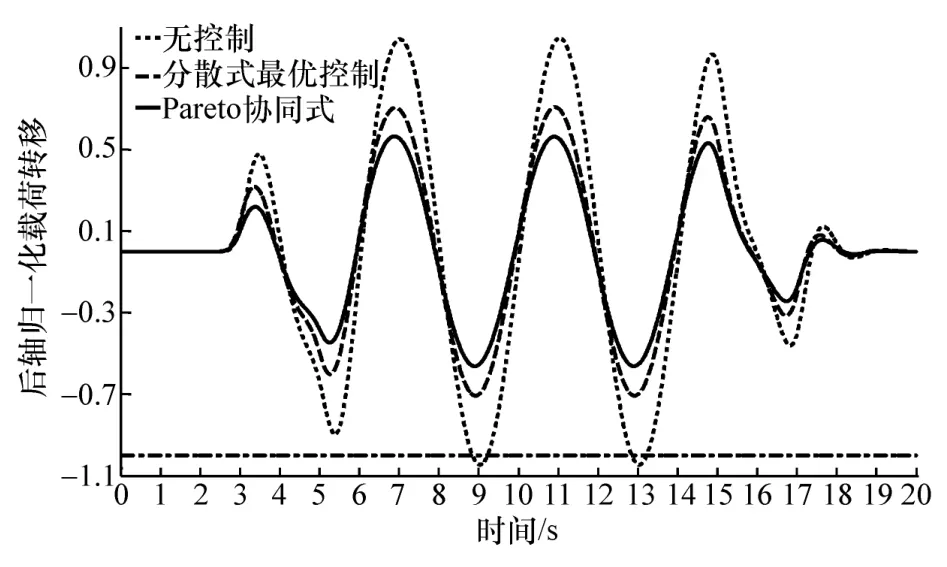
圖5 后軸歸一化載荷轉移

圖中的無控制是指車輛僅進行路徑跟蹤控制而不進行抗側傾控制，由于沒有側傾控制，后軸的歸一化載荷轉移超過-1，發生側翻；相比于無抗側傾控制情況，分散式最優控制可顯著提高車輛側傾穩定性，而Pareto協同式最優對側傾穩定性的提高效果明顯好于分散式最優，分散式最優控制和Pareto協同式最優控制輸入力矩如圖6所示，后者的輸入力矩要稍微大于前者。

為分析3種情況下車輛路徑跟蹤的控制效果，選取3種控制方法下車輛的橫向位置，航向角進行比較分析，如圖7和圖8所示。

通過比較無控制與分散式最優兩種控制算法下車輛的橫向位置和航向角，可發現無控制下車輛的橫向位移和航向角都更接近期望路徑，這可能是由于分散式最優控制中的側傾控制輸入對橫向控制產生影響，而基于Pareto最優均衡理論設計的協同式最優控制策略，路徑跟蹤效果明顯好于無控制與分散式最優控制，說明Pareto協同式最優控制策略可減小抗側傾控制輸入對橫向路徑跟蹤效果的影響。

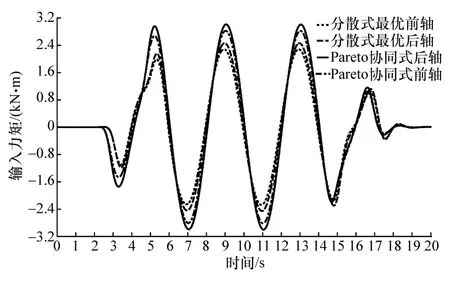
圖6 兩種控制策略下前后軸抗側傾力矩

圖7 不同控制算法下的橫向位移

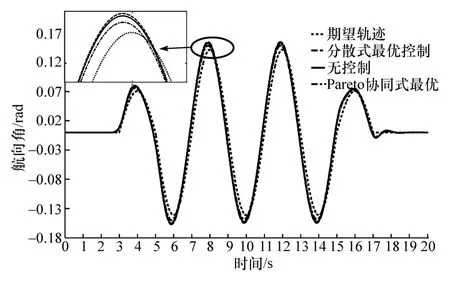
圖8 不同控制算法下的航向角

由于車輛的操縱穩定性與側傾穩定性相互耦合，車輛橫擺角速度與側傾角呈復雜的非線性關系［21］，因此有必要判斷施加的主動抗側傾力矩對操縱穩定性的影響，車輛的操縱穩定域可由相平面ββ′得到，且可用穩定性指標 λ評估［22］，λ如式（35）所示，當λ≤1時，商用車處于穩定域內。

在分散式最優和Pareto協同式最優兩種控制方法下的β-β′相平面和λ如圖9和圖10所示。

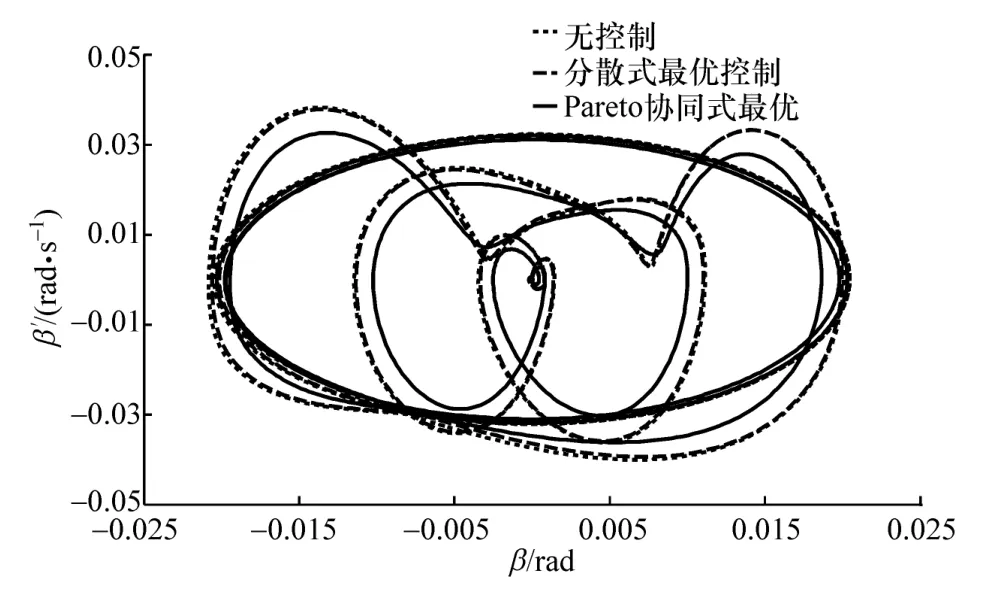
圖9 β-β′相圖

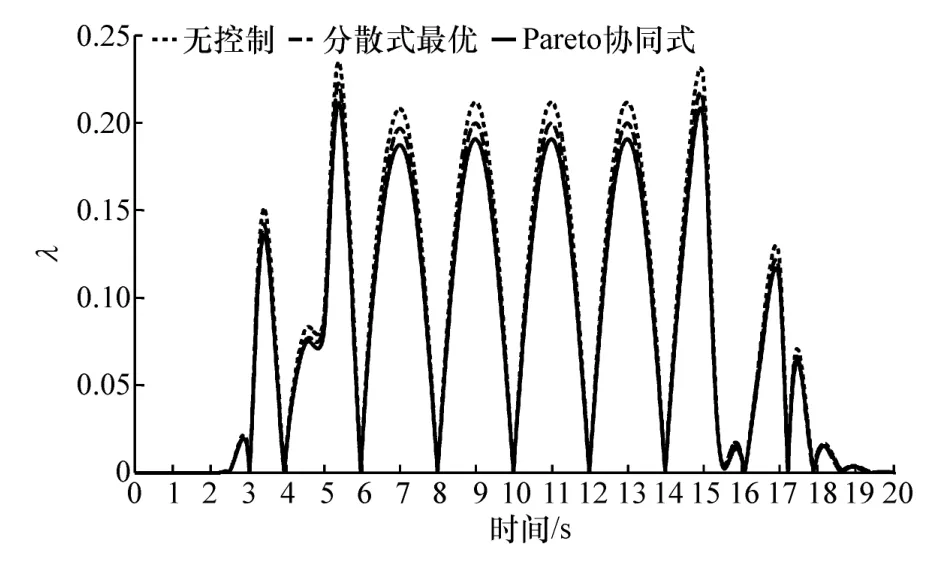
圖10 操縱穩定性指標

由圖可以看出，Pareto協同式最優控制下車輛的橫向穩定性明顯好于無抗側傾控制和分散式最優控制。

4 結論

本文中建立了5自由度智能商用車-道路閉環模型，基于線性二次最優理論設計了路徑跟蹤橫向-抗側傾分散式最優控制器，基于Pareto最優均衡理論設計了Pareto協同式最優控制策略，基于智能車-道路閉環模型對兩種控制策略進行了仿真驗證。仿真結果表明，相比于分散式最優控制策略，Pareto協同式最優控制策略能夠減小橫向與抗側傾控制之間的耦合，在提高車輛路徑跟蹤精度的同時顯著提高車輛的橫向和側傾穩定性。