基于飛行科目統計分析的嚴重譜編制方法

張佳佳，蔣祖國，馮建民

(1.中國飛機強度研究所 全尺寸飛機結構靜力/疲勞航空科技重點實驗室，西安 710065) (2.中國飛行試驗研究院 強度部, 西安 710089)

0 引 言

在現有試驗技術水平下，國內飛機的全尺寸疲勞試驗一般需要花費較長的時間(一般為4倍壽命，5～8年)，已經成為影響型號研制周期的關鍵因素之一[1]。過長的疲勞試驗周期，成為制約我國飛機研發的瓶頸，影響著整個飛機技術和產業的發展[2-4]。通過對飛機結構壽命分散性的研究，提出分散系數與載荷譜嚴重程度有關的觀點[5]，即采用嚴重譜可以減小疲勞壽命分散系數[6]，能夠大幅縮短試驗時間至2倍壽命，具有重大的工程意義。

2008年，國軍標GJB 67.6A-2008對編制耐久性嚴重載荷譜提出了明確要求[7]，但由于國內在嚴重譜方面研究較少，目前絕大多數型號編制和使用的飛機載荷譜仍為平均譜，即代表飛機平均使用情況的疲勞載荷譜[8]。平均譜只能夠代表50%的損傷覆蓋率和使用壽命期內機隊50%飛機的預計使用情況，其代表性和真實性遠遜色于嚴重譜。

嚴重譜的概念在美國國防部發布的新版聯合使用規范指南《飛機結構》(JSSG-2006)[9]中首次提出“編制耐久性設計使用載荷譜，以反映飛機在設計使用分布內的嚴重使用情況，從而使機隊90%的飛機滿足預期使用壽命”。從損傷角度來說，耐久性載荷譜應反映90%載荷損傷覆蓋概率下的使用情況；從壽命角度來說，嚴重譜代表了使用壽命期內機隊至少90%飛機預計的使用情況[10]。

飛機結構設計思想對損傷容限設計和耐久性設計提出了新要求[11]。解決編譜問題對新一代飛機的研制和定壽，貫徹執行新的國軍標都迫在眉睫，是研究嚴重譜分散系數，嚴重譜下結構使用壽命[12]和嚴重譜工程應用等后續研究的基礎。

國內外針對不同類型的載荷譜有不同的編制方法，早期歐洲使用的是TWIST方法[13]編制飛續飛隨機譜，為加速全尺寸疲勞試驗歷程，提出了雨流計數和等損傷折算的簡化編譜方法[14]。FAA通過對通用類航空飛機標準過載數據的統計分析，編制出了單機和各個作業機組的突風譜和機動譜[15]。國內采用的基本編譜方法是任務分析法[8]，在其基礎上做出了代表中值損傷、結合飛行大綱、全信息代表飛行起落法等探索[16-19]。

為了編制嚴重譜，國內學者討論了載荷譜損傷分散性的描述方法[20]，闡明了壽命分散性的含義，提出了嚴重譜損傷選取準則，并建立了基于載荷因子-累計超越數曲線族[21]的嚴重譜的包線選取方法[22]，但沒有得到基于任務分析法的具體嚴重譜編制方法與結果，對于嚴重譜的編制流程和參數選擇，尚無明確方法與步驟。

本文以我國某教練機標準化后的起落數據為基礎，提出基于飛行科目統計分析的嚴重譜編制方法，建立完整的編譜流程，計算出加權平均譜，一倍、兩倍標準差譜，90%/95%嚴重譜的使用情況，得到飛行科目嚴重譜和總嚴重譜；通過K-S檢驗方法驗證載荷損傷分布的合理性，根據當量損傷計算結果給出嚴重譜代表起落的選取方法。

1 數據選擇與編譜方法

1.1 原始數據與任務剖面的選擇

原始數據為某教練機實測重心過載譜經過標準化處理后的起落數據，含8種任務剖面的246個飛行起落數。參考文獻[8]給出的飛機編譜用典型任務剖面的飛行科目，包含飛行起落數、一次飛行時間、使用時間比例、起落代號等參數，具體參數如表1所示。

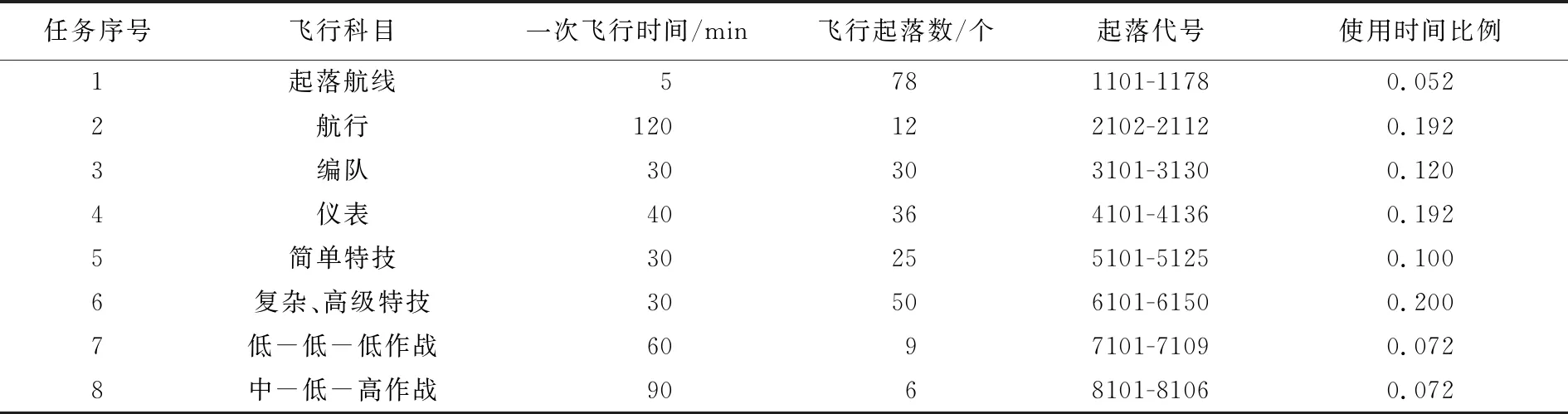
表1 典型飛行科目參數表

1.2 飛行科目統計分析法的基本思想

編制嚴重載荷譜的飛行科目統計分析法結合了國內編制載荷譜的任務分析法[8]與FAA處理載荷數據的統計思想[15]，以機隊飛機飛行科目為編譜單元，由此編制機隊飛機每個飛行科目的嚴重譜和總嚴重譜。

2 嚴重載荷譜編制

本節以編制重心法向過載為主參數的參數嚴重譜為例來闡述飛行科目嚴重譜編制方法的具體實施步驟，重點討論其計數、擬合、統計等步驟。

2.1 計數統計處理

輸入機隊飛機飛行科目壓縮的重心過載及飛參歷程后，按雙參數循環計數法分別計數該起落重心法向過載nz的所有峰值和谷值，對于每個起落，采用了首尾相連的辦法使其成為全循環或半循環譜。計數的峰值用加權平均的方法歸并到相應的載荷級中，對于國內教練機起落數據，確定了以0.5為間隔的10個載荷級，即峰值范圍1.5～6.5，谷值范圍-0.5～4.5。統計每個飛行科目每次飛行各級nz及相應輔助參數實有出現頻數。

實有頻數計數完成后，分別計算同一飛行科目每次飛行的峰值載荷和谷值載荷的累積頻數，并標準化1 000飛行小時。假設某型飛機有m個飛行科目，每個科目含n次起落飛行，則一共要計算2mn個重心載荷nz累積頻數譜。

2.2 確定載荷情況

所謂確定載荷情況，就是如何組合飛行科目剖面的性能參數、結構載荷環境的響應參數和其他相關參數，以形成不同的載荷狀態，作為載荷計算和應力分析的輸入。一般用飛行參數的統計分布組合方法來確定載荷情況[8]。

2.3 參數擬合

參數擬合包括曲線擬合和高載外推擬合。參數擬合能更好把握機群過載與累積頻數的關系，由此形成飛行科目擬合函數曲線，便于編譜的后續處理。

由于本文使用對數多項式進行擬合，故在進行曲線擬合時，對負的載荷谷值，取nz=|nz|；對0過載，取nz=0.01。

2.3.1 曲線擬合

在一般情況下，可用如下對數多項式方程進行曲線擬合

lgy=a0+a1x+a2x2+a3x3+a4lg(x)

(1)

當編制以重心過載nz為主參數的嚴重載荷譜時，可把式(1)變成如下形式

(2)

式中：F(nz)為各級重心載荷nz的累積頻數；nz為重心法向載荷；a0，a1，a2，a3，a4為曲線擬合得到的系數。

當取a0，a1，a2，a3，a4中的兩項或三項為0時，可獲得較好的擬合性[15]。通過最小二乘法進行擬合，擬合結果為曲線與原始數據偏離最小且變化趨勢相同。

2.3.2 高載外推

盡管通過實測起落數所獲得的編譜數據考慮了各種使用情況和所有飛行科目，大載荷出現的概率更大些，但畢竟飛機是在和平環境下的訓練飛行或運營飛行，飛機在極端惡劣環境中飛行的機率很小，很難出現一個壽命期內等于或大于最大載荷的情況，因此編制嚴重譜需要更多地考慮飛機最嚴重的使用分布情況。考慮到編譜數據的局限性，編譜過程中需要進行高載外推。

用對數線性外推方法對擬合曲線進行外推，令式(2)中的a2，a3和a4均為0，由此可得對數線性外推的一般方程

lg[F(nz)]=a0+a1nz

(3)

用式(3)進行外推時，每次飛行擬合曲線最高兩級的載荷和累積頻數作為原始數據進行線性擬合，得到每次飛行外推的對數線性方程。

2.4 繪制飛行科目載荷擬合函數曲線

根據建立的曲線擬合方程和高載外推方程，繪制含外推部分的飛行科目載荷擬合函數曲線，如圖1所示：圖中為高級復雜科目的2×50條曲線。

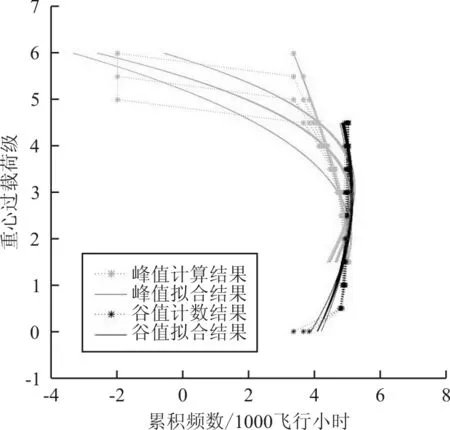
圖1 復雜高級特技科目曲線擬合結果

2.5 計算加權平均值和標準差

根據某飛行科目的n次飛行起落的n條重心過載nz的擬合曲線，可得到各級過載nz的累積頻數y(即F(nz))，由此可按式(4)和式(5)計算加權平均值yw和加權標準差sw。

(4)

(5)

式中：ti為第i次飛行起落該飛行科目的飛行小時數；T為該型號飛機該飛行科目的總飛行小時數；yi為第i次飛行起落該飛行科目各級載荷(重心過載)累積頻數。

該型號中的每架飛機在執行同一飛行科目任務時，其飛行結果具有較大的分散性，計算加權平均值和加權標準差是為了抵消這種分散性。由于該型飛機有m個飛行科目，需要計算m次加權平均值和加權標準差，本文中m=8。

2.6 計算置信度譜

考慮到國軍標GJB67.6A-2008規定的耐久性嚴重載荷譜是按90%存活概率給出，本文的最終嚴重載荷譜按90%概率值、95%置信度值的置信度譜確定，該置信度譜簡稱90%/95%譜，90%/95%譜的數學表達式如下

Y90/95=μ+δ

(6)

式中：Y90/95為存活概率90%、置信度95%的載荷累積頻數；μ為置信度為95%時的總體平均估計值；δ為相應于存活概率為90%時的總體分散度。

在一般情況下，總體平均值μ的90%置信度值可由式(7)求得

(7)

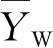
90%存活概率的分散度δ的相應計算式如下：

δ=1.282σ

(8)

(9)

根據式(4)～式(9)的計算結果，編制出該機隊的加權平均譜和各種嚴重載荷譜，包括(μ+1σ)譜、(μ+2σ)譜和90%/95%譜。

2.7 編制飛行科目加權平均譜和各種嚴重譜

根據2.5 節和2.6節的計算結果，編制每個飛行科目的加權平均譜和各種嚴重載荷譜，復雜高級特技科目嚴重譜編制結果如圖2所示。

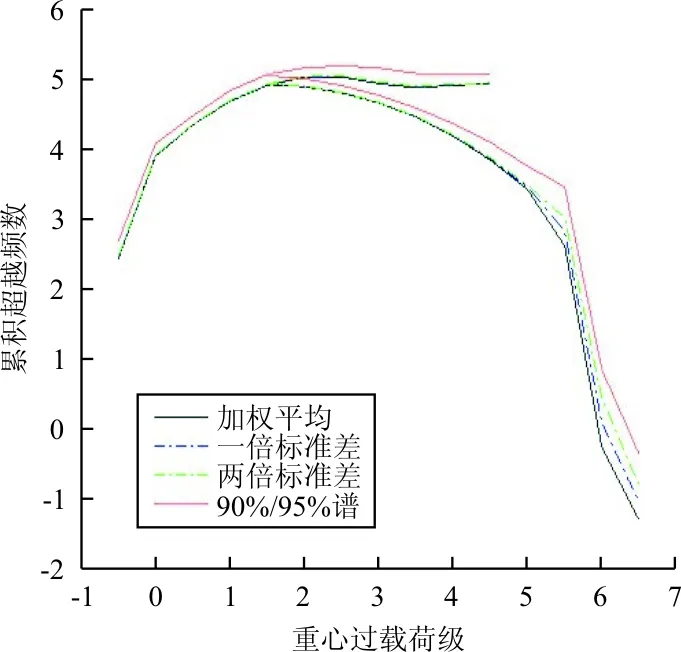
圖2 復雜高級特技科目嚴重譜編制結果

2.8 編制總譜

由飛行科目剖面資料可獲得每個飛行科目的使用百分比μi，把所有的μi用矩陣形式表示為

M=[μ1,…,μi,…,μl]

(10)

式中：M為飛行科目的使用比例矩陣；μi為第i個飛行科目的使用百分比，由該科目一次飛行時間與飛行總時間的比值計算；l為飛行科目數。

飛行科目的使用比例矩陣M乘以飛行科目譜矩陣F即為總譜G，即

G=M·F

(11)

或

(12)

式中：G為總的各級載荷累積頻數矩陣；gj為第j級載荷累積頻數，編譜結果如圖3所示。

圖3 飛行科目統計方法總嚴重譜編制結果

3 嚴重譜代表起落的選取方法

本文根據當量損傷值的統計分析結果選取嚴重譜代表起落。

3.1 當量損傷的計算方法

針對某教練機飛機下翼根部關鍵部位，采用線性累積損傷理論[23]和奧丁變換法進行當量損傷的計算。

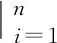
(13)

式中：f(ΔGi,Ri)為第i次循環對應的當量損傷。

3.1.1 當量損傷的理論基礎

指定應力比下的S-N曲線用冪函數表示，即

SmN=C

(14)

根據線性累積損傷理論，單個循環損傷為

(15)

式中：Ci，Si為第i次應力循環下的S-N曲線參數；Ni為給定循環下的壽命。

累積各次循環損傷得到全部循環損傷為

(16)

將各次載荷循環當量折算為等損傷的脈動循環S0i，得到

(17)

式中：C,m為脈動循環下S-N曲線參數。

在工程上可以略去少量其他載荷狀態循環與亞音速對稱狀態的差別[3]，故在飛機對稱飛行占主導地位的情況下，可以假定關鍵部位的應力與過載成線性關系。即有

Si=σlg·Gi

(18)

式中：σlg為單位過載對應的關鍵部位名義應力。

將式(18)帶入式(17)，即

(19)

引入與dn呈線性關系的當量損傷為

(20)

式中：ΔG0i為第i次過載循環對應的脈動過載變程。

3.1.2 確定當量損傷的關鍵問題

由式(20)，確定當量損傷，關鍵問題是確定S-N曲線參數m的值和每個載荷循環的當量脈動過載變程ΔG0i。

m值應綜合多個材料、結構形式不同的關鍵部位進行選取。文獻[24]給出了綜合考慮飛機結構多個關鍵部位不同材料及細節形式，在一般飛機載荷歷程下的m值在4左右的結論。本文中取m=4。

計算當量損傷可采用奧丁變換方法，將任一級過載循環(ΔGi,Ri)等損傷折算為當量脈動循環ΔG0i。

(21)

3.2 當量損傷的分布檢驗

以復雜高級特技飛行科目為例，對于每個起落，雨流計數時抽取其中的全循環與半循環，由式(21)算每個起落的當量損傷。驗證其損傷分布合理后，即可按統計方法進行代表起落的選取。

3.2.1 分布形式

對于軍機機群載荷損傷分布，一般認為其符合對數正態分布：

(22)

式中：μ為對數正態期望；σ為對數正態分布標準差。

將分布函數線性化后得到標準正態分布的線性檢驗方程：

lgx=μ+upσ

(23)

式中：up為標準正態分布p分位點。

3.2.2 K-S檢驗方法

哥爾莫柯洛夫-斯米爾諾夫(K-S)檢驗方法需要檢驗的假設是

H0∶f(X)=F0(x)

(24)

式中：F0(x)為完全確定的(不包含任何未知參數)連續型分布函數。

為了尋找檢驗統計量，將子樣(x1,x2,…,xn)的各分量按大小重新排成x(1)≤x(2)≤…≤x(n)。子樣的經驗分布函數Fn(x)為

(25)

K-S檢驗統計量為

(26)

只要給定了顯著度α就可按條件

P(Dn>Dn,α)=α

(27)

從K-S檢驗臨界值(Dn,α)表中查出Dn,α值。

現計算Dn的取值，由于Fn(x)為單調非降階梯函數，F0(x)為單調非減函數，所以|Fn(x)-F0(x)|的上確界可在n個點X(i)(i=1,2,…,n)處找。用δi表示X(i)處的經驗分布函數與假設的分布函數之間偏差中大的一個，即

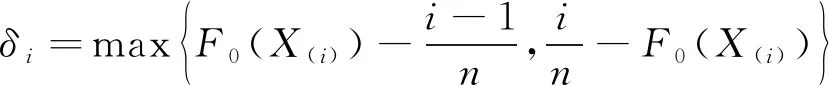
(28)

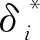
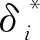
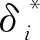
3.2.3 載荷損傷值的分布檢驗

針對復雜高級特技這一科目50個起落的損傷計算結果，用K-S方法進行檢驗，假設損傷值滿足對數正態分布。

當量損傷的計算結果為(按升序排列，取對數)：

1.859 3 2.043 0 2.094 5 2.138 8 2.159 5

2.210 6 2.319 4 2.342 2 2.354 0 2.412 5

2.439 4 2.467 1 2.502 8 2.503 8 2.576 4

2.601 6 2.613 8 2.637 4 2.655 9 2.662 6

2.666 9 2.671 4 2.692 4 2.707 1 2.718 6

2.801 7 2.902 3 2.943 0 2.946 5 2.948 6

2.973 3 2.976 0 3.084 1 3.092 0 3.132 4

3.154 2 3.185 9 3.246 0 3.265 8 3.389 9

3.620 0 3.679 8 3.725 2 3.757 6 3.770 5

3.786 5 3.844 5 4.259 6 4.944 7 6.212 2

均值為2.973 9，標準差為0.771 2。

假設對數損傷值X滿足正態分布N(2.973 9，0.771 22)即原假設為

H0(X)∶X·N(2.973 9，0.771 22)

(31)

要求X的分位數Xα可轉化為求N(0,1)的分位數，此時有

xα=σzα+μ

(32)

由式(32)計算得到每個樣本對應分位數Xα，查標準正態分布表得對應的分布函數值F0(Xi)。

當顯著度取0.05時，查表得K-S檢驗臨界值D50，0.05=0.189>0.14

當顯著度取0.10時，查表得K-S檢驗臨界值D50，0.10=0.169>0.14

故接受假設H0，即當量對數損傷值滿足標準正態分布，因此損傷值滿足對數正態分布。

3.3 根據損傷統計結果選取嚴重譜代表起落

經檢驗損傷值合理[26]，故可將損傷結果按照第2節中的思想進行統計分析處理，得到與加權平均譜、一倍標準差嚴重譜、兩倍標準差嚴重譜，90%/95%譜相對應的損傷值，再根據與其最接近的損傷值對應的起落作為嚴重譜的代表起落，并記錄對應的起落編號。

下表是根據當量損傷值統計分析選取復雜高級特技這一飛行科目的代表起落的結果。

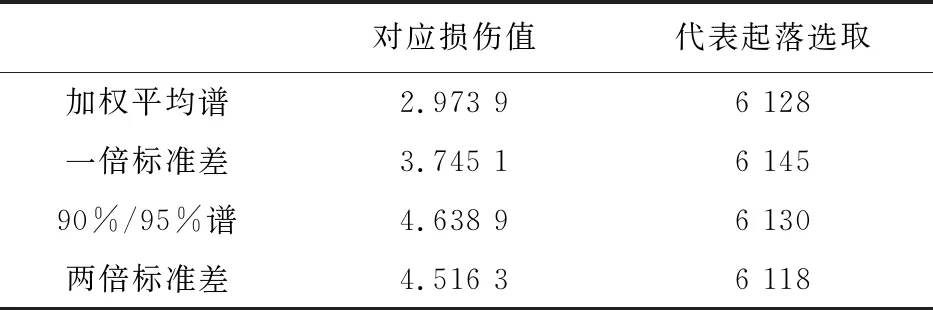
表2 嚴重譜代表起落選取

按當量損傷統計分析方法選取的代表起落真實有效，載荷譜損傷較大時，試驗時間相應縮短。此方法實用性強，可以應用到按不同嚴重程度進行5×5試驗譜或飛—續—飛譜等后續編制工作。

4 結 論

(1) 本文基于飛行科目統計分析的編譜方法，針對我國某教練機給出了加權平均值譜，1倍標準差譜，2倍標準差譜，以及90%存活概率和99%置信度的嚴重載荷譜。

(2) 通過觀察載累積頻數分布曲線，起落越多，載荷分散性越大。由于飛行科目差異，起落情況復雜，載荷峰值載荷分散性較大，谷值載荷分散性較小。

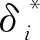
(4) 采用嚴重譜可以降低疲勞分散系數以縮短試驗時間，在我國各機型的全機疲勞試驗中有廣闊的應用前景。