考慮不完全維修的裝備單元維修與更換策略優化
陳陽隆, 馬彥恒, 侯建強
(陸軍工程大學石家莊校區無人機工程系, 河北 石家莊 050003)
傳統的預防性維修主要是指定期維修,它存在維修不足或維修過剩的問題[1]。隨著現代科學理論與技術的發展,視情維修逐漸發展成為預防性維修的主要方式。基于認知測試性設計[2]的裝備可以實時的評估自身狀態。當裝備狀態不滿足任務要求時,可視情制定維修策略,安排相應的維修措施,使裝備及時、準確地消除潛在隱患,提高運行的可靠性,降低突發故障帶來的經濟損失及安全問題。
在視情維修決策建模中,維修效果是對失效單元修后性能恢復程度的衡量。維修效果主要包括完全維修(修復如新)、不完全維修和最小維修(修復如舊),其中基于完全維修和最小維修的建模理論相對較為完善[3]。由于不完全維修介于完全維修和最小維修之間,其更加貼合工程實際,已成為當前維修建模研究的熱點問題[4]。如:WU等[5]介紹了現有不完全維修模型中存在的共性問題,并依據維修后系統的退化方式,將不完全維修模型分為線性與非線性2大類;程志君等[6]采用馬爾科夫鏈建立了系統退化維修模型,通過狀態轉移率表征不完全維修;潘剛等[7]采用Semi-Markov模型描述裝備單元的性能衰退過程,提出了預防性維修和修復性維修相結合的不完全維修決策方法;LIU等[8]將裝備單元的狀態轉移率與維修次數相關聯,采用準更新過程理論描述裝備單元的壽命變化情況,建立了基于非齊次連續時間的馬爾可夫視情維修決策模型。
綜上所述可以看出:當前研究僅考慮了維修次數對維修效果的影響,且建立的不完全維修模型雖然表達了維修效果中的修復非新思想,但并未考慮維修后裝備單元衰退速度的變化。筆者首先將維修費用和維修次數引入不完全維修模型,并假設各裝備單元維修后均處于最高性能狀態(并非修復如新);其次,采用性能狀態衰退速度來描述不完全維修的維修效果,采用齊次馬爾科夫模型來表征裝備單元的衰退規律;最后,結合準更新過程建立不完全維修模型,并針對不同裝備系統的任務性能需求,尋找最優的裝備單元維修費用和更換策略,實現裝備系統單位時間的凈效益最大化。
1 模型假設與描述
1.1 模型假設
1) 裝備系統L由M個裝備單元s構成,其中連接方式可以是任意的,如串并聯結構。
2) 裝備單元s(s=1,2,…,M)有ks個不同的狀態。其中:g(s,i)為裝備單元s處于狀態i(i=1,2,…,ks)時的性能水平,表征裝備單元s對裝備系統正常運行的貢獻度;ps,i(t)為裝備單元s在t時刻處于狀態i的概率。
3) 裝備單元的狀態轉移過程符合齊次馬爾科夫模型。
4) 裝備單元狀態監測費用忽略不計,當監測到裝備單元狀態低于維修閾值時,即進行預防性維修或更換,且維修為不完全維修,同時預防性維修成本<更換成本。
5) 維修效果與維修費用有關,其函數關系可通過歷史數據得到。
6) 裝備單元每次維修的維修費用是一致的。
7) 優化目標為在滿足裝備系統的任務性能需求下,優化裝備單元s的維修費用cs和更換策略Ns(即預防性維修次數),使裝備系統單位時間的凈效益最大。
8) 裝備單元采取維修措施后,裝備恢復到最高性能狀態,但并非修復如新,修復后的裝備單元的性能衰退速度加快,即狀態轉移率會增大。
1.2 模型描述
隨著認知測試性技術的發展,可以實時監測裝備中各裝備單元的狀態。當裝備單元狀態低于維修閾值時,可采取維修或更換措施,使其得到不同程度的恢復。當采取維修措施時,修后裝備單元的狀態為不完全修復狀態,且隨著維修次數的增加,裝備單元的可靠性將快速下降,進而影響裝備任務的完成。因此,筆者考慮不完全維修,根據裝備系統的任務性能需求,建立裝備單元維修與更換策略權衡優化模型,為裝備系統中每個單元選擇最優的維修費用和更換策略,使裝備系統單位時間的凈效益最大,即
C=Cp-Cq-Ca;
(1)
(2)
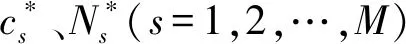
2 模型建立
2.1 基于齊次馬爾科夫模型的裝備單元瞬時狀態概率模型
采用馬爾科夫模型[9]的離散狀態來描述裝備單元的性能狀態。設X(t)∈{1,2,…,k}為裝備單元在任意時刻t的狀態集合,則根據馬爾科夫性有
P{X(tn)=xn|X(t1)=x1,X(t2)=x2,…,
X(tn-1)=xn-1}=P{X(tn)=
xn|X(tn-1)=xn-1},
(3)
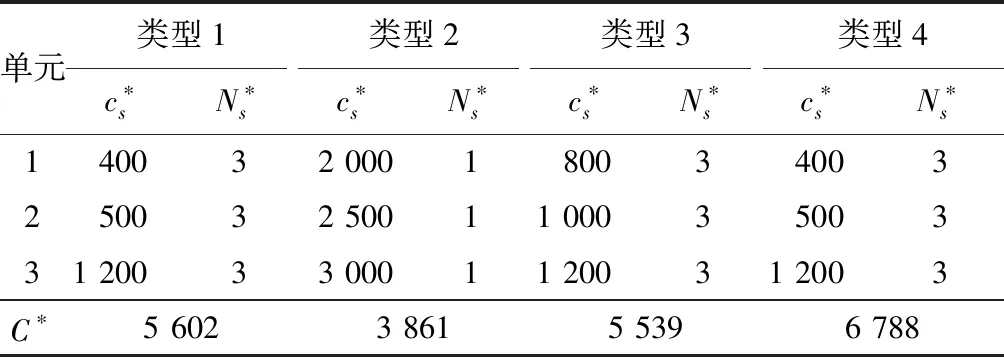
式中:X(tn)=xn,表示在tn時刻裝備單元的狀態為xn,0≤t1 裝備單元在t(t≥0)時刻的狀態i(i=1,2,…,k),經Δt(Δt≥0)后轉移到狀態j(j=1,2,…,k,j≠i)的狀態轉移概率為 Qi,j(t,t+Δt)=P{X(t+Δt)=j|X(t)=i}= λi,j(t)·Δt+o(Δt),i≠j, (4) 式中:λi,j(t)為裝備單元在t時刻離開狀態i轉移到狀態j的狀態轉移率;o(Δt)為Δt的高階無窮小。若λi,j(t)為與時間無關的常數,則該過程為齊次馬爾科夫過程;反之,則為非齊次馬爾科夫過程。 由圖1可知:裝備單元s的狀態轉移率矩陣 (5) (6) 設裝備單元最低狀態為維修閾值狀態,當達到該狀態時,立即對裝備單元進行維修。修后裝備單元恢復至最高性能狀態,但并非修復如新,在新的運行周期中裝備單元的性能衰退速度將加快。運用準更新過程理論[11-12],將裝備單元第r-1次與第r次維修之間的時間間隔定義為第r次維修周期,采用隨機變量Hr來描述第r次維修周期中裝備單元的壽命,且滿足 H1=Z1,H2=αZ2,…,Hr=αr-1Zr, (7) 式中:Zr為獨立同分布隨機變量;H1,H2,…,Hr,…為一個以α(α>0)為參數的準更新過程。在不同維修周期中,裝備單元壽命的變化情況為:當0<α<1時,裝備單元壽命隨著維修周期的增加而減小;當α=1時,裝備單元壽命保持不變;當α>1時,裝備單元壽命隨著維修周期的增加而增加。且有 (8) 采用裝備單元的狀態概率表示可靠度,結合式(8)與可靠性理論可得[13-14]: (9) (10) (11) (12) 式中: (13) (14) (15) (16) 通用生成函數作為一種簡潔、高效的離散隨機變量組合運算工具,已被廣泛地運用于裝備系統的狀態評估和可靠性研究等領域中。裝備是由一系列裝備單元按一定的結構關系構成的有機整體,因此可采用通用生成函數[15]由裝備單元的穩態概率分布計算出裝備系統的穩態概率分布。由式(12)求出的裝備單元s的穩態概率分布的通用生成函數為 (17) 式中:z沒有具體的取值,主要用于區分狀態性能g(s,i)和對應的概率ps,i。則整個裝備的穩態概率分布為 UL(z)=?{u1(z),u2(z),…,uM(z)}= (18) 式中:“?”為通用生成函數中的求和算子;is(s=1,2,…,M)為裝備單元s的狀態變量,pL,i為裝備系統L在狀態i的穩態概率;g(L,i)為裝備系統L在狀態i時的性能水平;kL為裝備系統最大可能的狀態數;W(·)為裝備系統的結構函數。當電流傳輸型系統由2個單元串聯組成時,有 W(g1,g2)=min{g1,g2}; (19) 若為并聯,則有 W(g1,g2)=g1+g2。 (20) 根據式(1)裝備系統單位時間的凈效益和裝備系統單位時間的性能水平的期望值,可得裝備系統單位時間的性能水平回報 (21) 式中:ce為裝備系統在單位時間內單位性能水平下的回報量。 在策略Ns下,裝備單元s的單位時間維修費用 (22) 則整個裝備系統單位時間的維修費用 (23) 設裝備系統的最低任務性能需求水平為w,當裝備系統性能水平低于w時,需要進行補償,則裝備系統性能水平不滿足任務需求水平w時,帶來的性能補償 (24) 式中:cf為裝備系統在單位時間內單位性能水平不足時的補償量。 為使裝備系統單位時間的凈效益C最大,需要優化為裝備單元s安排的維修費用cs與更換策略Ns,權衡優化模型如式(2)所示。 為了解決求解空間維數爆炸問題,將裝備單元s的維修分為v(v=1,2,…,ns)個等級,則第v個維修等級對應的維修費用 (25) 以某無人機控制裝備為例,其由3個裝備單元構成,如圖2所示。其中:單元1、2有3個不同的性能水平,單元3有4個不同的性能水平。性能水平代表處于該狀態的裝備單元對裝備正常運行的貢獻度,一般狀態i越低,其對應的性能水平g(s,i)也將越小,一般結合裝備歷史數據通過分析裝備性能得到。裝備單元的性能水平與狀態轉移的率相關數據如表1所示。 單元性能水平/%狀態轉移率/(次·月-1)1g(1,3)=30λ13,2=0.30,λ13,1=0.40g(1,2)=20λ12,1=0.50g(1,1)=0 —2g(2,3)=45λ23,2=0.30,λ23,2=0.35g(2,2)=30λ22,1=0.45g(2,1)=0 —3g(3,4)=90λ34,3=0.30,λ34,2=0.35,λ34,1=0.40g(3,3)=70λ33,2=0.50,λ33,1=0.65g(3,2)=40λ32,1=0.85g(3,1)=0 — 根據各裝備單元的狀態轉移率,通過求解Kolmogorov微分方程組可得到各裝備單元的瞬時狀態概率分布分別為 P1(t)=(p1,1(t),p1,2(t),p1,3(t))= P2(t)=(p2,1(t),p2,2(t),p2,3(t))= P3(t)=(p3,1(t),p3,2(t),p3,3(t),p3,4(t))= (1-2e-1.15t+5.25e-1.05t-4.25e-0.85t, 5e-1.15t-9.25e-1.05t+4.25e-0.85t, 3(e-1.05t-e-1.15t),e-1.05t)。 各裝備單元的相關維修參數如表2所示。其中 表2 裝備單元s的維修決策參數 費用單位為元。 在裝備單元更換策略下,可得到裝備系統的穩態概率。根據式(18)可計算出裝備系統的狀態性能水平及其對應的概率。設ce=2,cf=0.8,w=60%,應用遺傳算法可得到裝備系統的優化結果,如表3所示。 表3 某無人機控制裝備維修決策優化結果 由表3可以看出: 1) 類型1的維修策略為:每次失效后安排的維修費用為400元,并在第3次失效后安排更換,其裝備系統的最大單位時間凈效益為5 602元; 2) 類型2為傳統的完全維修,即每次失效后采取更換措施,其裝備系統最大單位時間的凈效益比類型1減少31%; 3) 類型3為失效后對所有裝備單元采取相同維修等級(假設所有裝備單元都采取第2個維修等級,v=2),其裝備系統最大單位時間的凈效益比類型1減少1%; 4) 類型4為將裝備的任務需求性能水平降為w=20%,其裝備系統最大單位時間的凈效益比類型1增加21%。 通過以上類比分析表明:筆者將裝備單元性能與裝備系統性能進行關聯,考慮了不完全維修和裝備的任務需求性能水平,建立的權衡優化模型可給出最優的裝備單元維修與更換策略。 從維修實際出發,對裝備單元進行不完全維修,采用裝備單元狀態的衰退速度衡量裝備單元的維修效果,建立考慮不完全維修的裝備單元維修與更換策略權衡優化模型,并通過算例驗證了模型的有效性;利用該模型得出裝備系統的最優維修費用與更換策略,既能保證裝備系統任務的順利完成,又可實現裝備系統單位時間的凈效益最大化,進而避免過度維修帶來的損失;裝備系統在運行中,當某一裝備單元狀態達到維修閾值時,將觸發維修機制。由于 裝備系統是由眾多裝備單元組成的,因此易造成裝備系統停機頻率高的問題,為此,下一步將結合機會維修策略進一步完善模型,解決復雜裝備系統因維修造成的停機頻率過高的問題。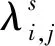


2.2 基于準更新過程的單元穩態概率模型
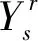

2.3 維修成本與維修效果關系模型
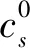
2.4 考慮不完全維修的權衡優化模型
3 算例分析


4 結論

